基于分块CS的梯度追踪算法在重构中的应用
2022-09-16刘艳,李雷
刘 艳,李 雷
(1.江苏电子信息职业学院 素质教育部,江苏 淮安 223002;2.南京邮电大学 非结构化数据计算理论与应用研究中心,江苏 南京 210046)
0 引 言
压缩感知(CS)[1-3]凭借能够从获得的少量数据中高概率地重构出原始信号的优点,在语音、图像及视频等方面应用广泛。该理论在图像方面的成果最先体现在Baraniuk教授等人提出的“单像素压缩数码照相机[4]”;随后在核磁共振(MRI)成像[5]、CT成像[6]及雷达遥感成像[7]中均得到了广泛的应用。
在处理高维图像时,随着数据规模不断增大,Lu等人提出了分块压缩感知[8],有效地解决了(CS)中计算量大、计算复杂度高、需要更多存储空间等问题。重构算法是压缩感知理论中的一个重要内容,随着对重构算法研究的深入,传统贪婪迭代算法由于计算量大而导致的重构效果不佳始终是一个需要面对的难题。为了解决这一问题,2008年,Thomas Blumensath和Mike E.Davies首先提出梯度追踪算法[9],随后,学者们提出了用优化算法中的最速下降梯度和共轭梯度计算逆矩阵的梯度追踪算法(Gradient Pursuit,GP)[10]和共轭梯度追踪(Conjugate Gradient Pursuit,CGP)[11]算法;文献[12-13]分别介绍了变步长的梯度追踪算法及基于拟牛顿法的梯度追踪算法(Quasi-Newton Method based Gradient Pursuit,QNMGP)[13]。为了充分发挥块压缩感知理论中计算量小和梯度追踪算法中不需要计算逆矩阵的优势,该文将两者结合,并通过具有下降性和二次终止性的L-BFGS算法计算更新方向,有效地将GP算法的思想运到分块压缩感知中,得到了重构性能更优的算法。
1 研究基础
1.1 压缩感知
1.1.1 压缩感知理论
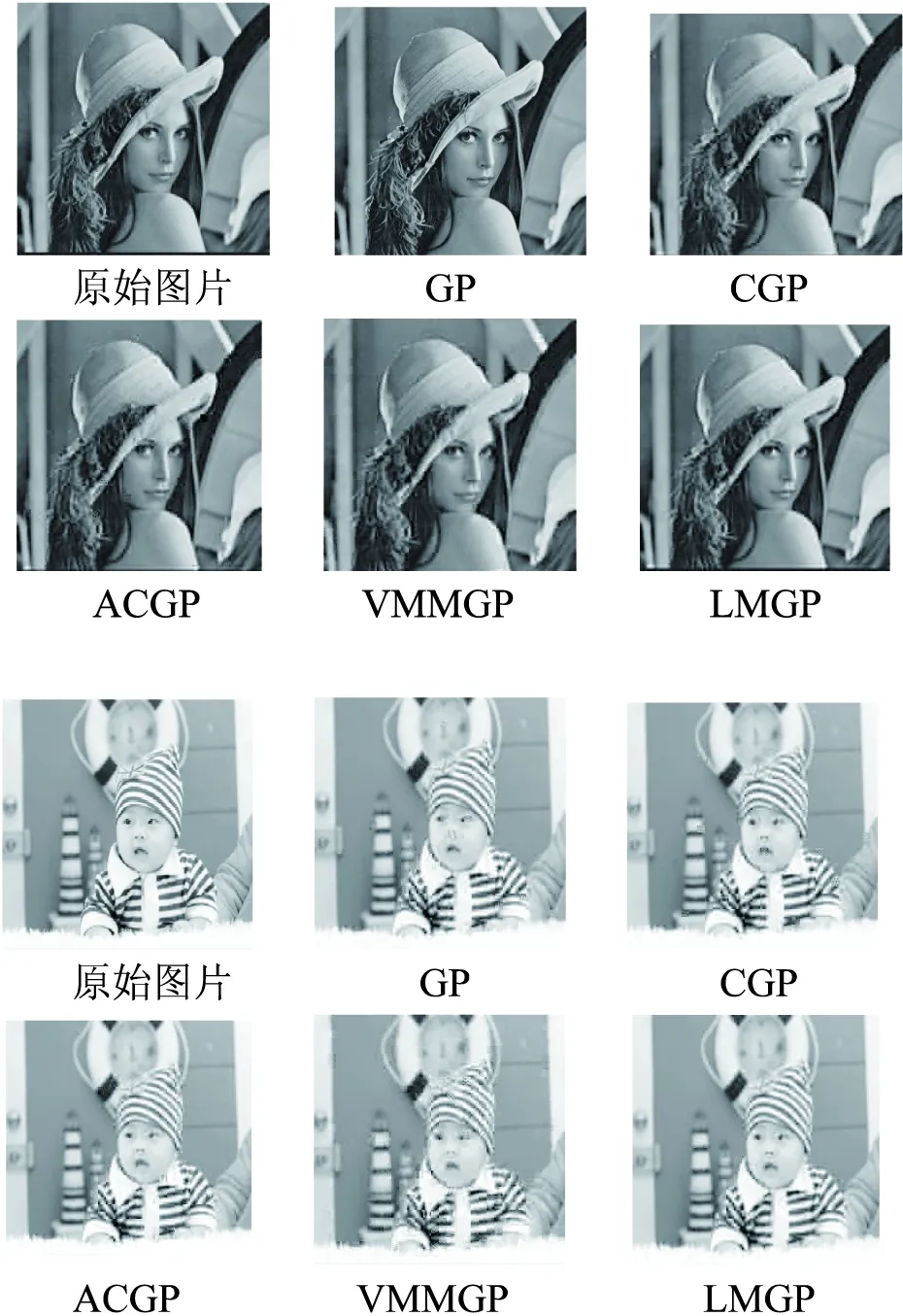
在压缩感知理论中,如果N维信号x是稀疏的,则可以通过M×N(M< y=Ax (1) 再通过重构算法对观测值进行恢复,就能大概率得到信号的近似重构。 1.1.2 分块压缩感知 将原图x∈RN×N分割成大小为B×B的互不重叠的m个图像块,第i块的图像块记作xi∈RB2,i=1,2,…,m,通过相同的观测矩阵AB对其进行观测,通过 yi=AB×xi (2) 得到观测值yi,其中AB∈RMB×B2,因此在整幅图像中观测矩阵A就可以表示成: (3) OMP算法求解的模型为: (4) 梯度追踪算法通过求解: (5) 牛顿法中的搜索方向由公式(6)确定: ▽2f(xk)d=-▽f(xk) (6) 将目标函数f(x)在xk+1点进行Taylor展开,得到二阶近似为: f(x)≈f(xk+1)+▽f(x-xk+1)+ (7) 式(7)两边关于x求梯度,令x=xk得: ▽f(xk+1)-▽f(xk)≈▽2f(xk+1)(xk-xk+1) (8) 令: sk=xk+1-xk,yk=▽f(xk+1)-▽f(xk) (9) 若Hesse矩阵可逆,则式(9)转化为: sk≈[▽2f(xk+1)]-1yk (10) 令n阶矩阵Hk+1≈[▽2f(xk+1)]-1,式(10)取近似为: sk=Hk+1yk (11) 称式(11)为拟牛顿方程[14]。由于式中变量数远大于方程数,故通过对Hk修正求解Hk+1,令: Hk+1=Hk+△Hk (12) Nocedal[15]提出的L-BFGS在一定的条件下,既解决了传统算法计算量较大的问题,也满足了全局收敛性。 BFGS的逆修正公式为: (13) (14) 记H0为初始矩阵,由式(12)可知,通过L-BFGS在第k+1次迭代可修正矩阵Hk+1。 当k+1≤m时: ⋮ (15) 当k+1>m时: ⋮ (16) 若H0是正定阵,则通过式(15)、(16)求解出的Hk+1也是正定阵。 由此可知,分块压缩感知所需存储空间远小于传统压缩感知观测采样所需空间,因此在对图像重构的过程中可以很大程度上减少重构时间。 LMGP算法采用OMP算法的原子选择策略。 LMGP算法通过方程: (18) 令: (19) LMGP算法步骤如下: 一:设初始误差r0=y,xn=0,Tn为空集,H0=I; 二:令n=1;n=n+1: (1)gn= (3)Tn=Tn-1∪in A.给定初始点x0,k=0,设置正整数m; B.设H0=I,求出目标函数f(x)在xk处的梯度▽f(x); C.求解方程组-Hk▽f(xk)=dk,得到dk; E.若‖▽f(xk)‖≤ε,停止迭代;若‖▽f(xk)‖>ε,进入下一步; G.令sk=xk+1-xk,yk=▽f(xk+1)-▽f(xk), H.k=k+1,返回步骤C。 (11)rn=rn-1-μncn 三:输出rn,xn,当满足‖rn-rn-1‖≤10-6停止。 故: (22) (23) (24) (25) (26) (27) 上述定理证明了提出的LMGP算法是可行的。 为了验证提出的算法在分块图形重构中的可行性,通过Matlab分别对标准图像“lena.jpg”及格式为jpg的一般图像进行仿真,将256×256的图像分割,取B=8,通过GP、CGP、ACGP、VMMGP与LMGP算法对图像进行重构,效果如图1所示。 图1 算法重构效果 如图1所示,相较于GP、CGP、ACGP、VMMGP算法重构出的图像,LMGP算法重构出的图像纹理更为清晰,更接近原始图像。 表1显示了GP、CGP、ACGP、VMMGP与LMGP算法在采样率为0.5时在“重构时间”、“均方误差”及“峰值信噪比”三方面的数据比较。 表1 同一采样率下各算法重构性能数据比较 如表1所示,相同采样率下,LMGP算法所需重构时间比CGP和VMMGP算法少;MSE较小;PSNR为27.303 7,远高于其他四种算法,由峰值信噪比越大效果越好可知:LMGP算法不仅具有可行性且图形重构质量更高。 表2显示了GP、CGP、ACGP、VMMGP算法分别与LMGP算法在整采样率分别取0.3、0.5和0.6情况下图像的峰值信噪比。 表2 不同采样率下各算法峰值信噪比数据比较 如表2所示,五种算法的PSNR均随着整体M/N的增加而增加,当M/N分别取0.3、0.5和0.6时,LMGP算法的峰值信噪比分别为25.317、27.303 7和27.561,均高于其余四种算法;同时可以看出随着采样率的增加,LMGP算法的PSNR增长速度逐渐降低,表明算法相对比较稳定。 图2以折线图的形式展现不同采样率下各种算法重构的峰值信噪比。 图2 不同采样率下重构性能比较 由图2可以看出,随着采样率的增加,几种重构算法的峰值信噪比均有所提高,LMGP算法在不同采样率下的峰值信噪比均高于其他算法。当采样率取值为0.3到0.5之间时,LMGP算法的峰值信噪比明显高于其他算法。由峰值信噪比越高图像重构效果越好可知,LMGP算法对图像的重构效果更好,算法性能更优。 在分块压缩感知的基础上,将L-BFGS算法与GP算法结合形成了LMGP算法并将其应用到图像的重建中,通过仿真将LMGP算法与传统的GP、CGP、ACGP、VMMGP算法进行比较,通过重构时间,MSE,PSNR三个方面的数据比较,LMGP算法的PSNR较高,重构时间较少,表明LMGP算法重构性能更优。1.2 OMP算法

1.3 GP算法
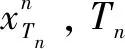
1.4 L-BFGS算法
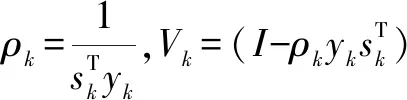
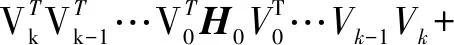
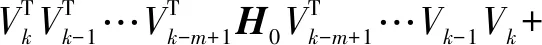
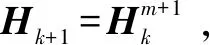

2 LMGP算法
2.1 LMGP算法描述
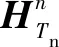
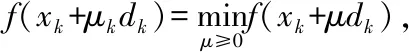
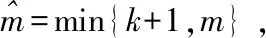

2.2 LMGP算法收敛性证明


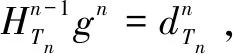




3 仿真结果及分析


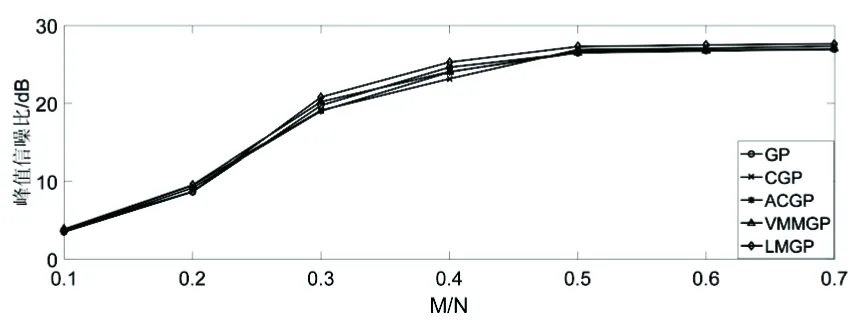
4 结束语
