粒径大小对颗粒堆积体Burgers模型蠕变参数相似试验研究

马志奇杨小彬刘腾辉李志辉

中国矿业大学(北京)应急管理与安全学院,北京 100083

颗粒堆积体是由块石、碎石、砂石等颗粒混合而成的不连续颗粒材料,其力学特性具有与时间相关的流变性质。随着颗粒堆积体的高度以及规模不断增加,堆积体的蠕变效应越来越明显,受上覆荷载引起的沉降和变形对生产危害很大,对于蠕变特性的研究也越来越受重视。颗粒堆积体沉降主要是由颗粒细观尺度上的运移引起的宏观变形,这就要求对颗粒的细观机制进行深入分析。颗粒尺寸是尤为重要的细观参数,直接影响颗粒材料的细观结构[1],进而造成颗粒材料宏观力学性质的变化。

室内蠕变试验主要是单轴蠕变试验[2]和不同围压下的三轴蠕变试验[3-8]。范登坡[9]研究了豫西某残坡积土的蠕变特性,探索了不同含石量的影响,建立了适合于不同含石量的残坡积土的蠕变模型。张庆建、付昱凯等[10-11]对泥岩进行三轴压缩蠕变试验,研究不同轴向应力下蠕变曲线变化规律,提出辨识模型参数的改进解析解法。王贺等[12]通过岩盐单轴压缩试验,选取四元件Burgers模型对试验曲线进行拟合分析,得到试验岩盐蠕变特性表征参数。杨珂等[13]对岩石进行分级加卸载试验,并用Burgers 模型对试验结果进行了拟合。

由Cundall 等[14]提出的颗粒流法及PFC 程序是求解非连续介质力学问题的一个重要数值分析方法。该程序将介质离散为大量的小颗粒单元,并通过颗粒之间的相互作用去描述、研究非连续岩石材料的力学特性。Kang 等[15]基于二维颗粒流程序(PFC2D),采用法向Hertz-Mindlin 模型、切向Burgers 模型进行了双轴蠕变试验的研究。王涛等[16]在PFC2D中开发出广义Kelvin 本构模型。郭鸿等[17-18]研究了分别和分级两种不同加载方式下黄土的蠕变特性,同时建立了Burgers 和离散元数值模型。张学朋等[19]采用颗粒离散元方法对微观颗粒之间的接触赋予Burgers 模型,验证了颗粒流Burgers 模型适用于岩石蠕变试验研究中。杨振伟等[20]基于三维颗粒流程序(PFC3D),采用Kelvin模型和Maxwell 模型串联组成的Burgers 流变模型,通过控制变量法,分析了Burgers 模型中弹性系数(Em和Ek)、黏性系数(ηm和ηk)和摩擦因数f对瞬时强度特性和流变特性的影响。

本文以玻璃微珠为实验材料,通过实验室试验,研究不同粒径的玻璃微珠在分级加载下的蠕变特性,分析粒径对四元件Burgers 模型4 个参数的影响,并建立离散元数值模型,实现宏观Burgers 模型参数到微观参数之间的转换,从而对试验结果进行验证。

1 试验方案与结果

1.1 试验方案

试验材料选用不同粒径的玻璃微珠,玻璃微珠是近年来发展起来的一种用途广泛、性能特殊的新型岩石材料,其主要成分为SiO2(75%),与砂土的成分相似。玻璃微珠作为一种岩石材料,成圆率高,并且具有一定的力学强度。本次试验选用粒径为0.6～0.8 mm、1～1.5 mm、2～2.5 mm 的玻璃微珠,如图1所示。

图1 玻璃微珠颗粒实物Fig.1 Photograph of glass bead particles

颗粒试样装填在长度80 mm、直径25 mm 的胶套内,均分5 次逐层装填,并轻微压实。试验前用针头排出胶套中空气,保证压头与颗粒贴合。试样装填实物如图2所示。

图2 玻璃微珠装填实物Fig.2 Photograph of glass bead loading

分级加载试验采用油泵控制的伺服三轴压力机,通过软件伺服控制轴压、围压的加载速率。计算机自动记录整个试验过程中应力、轴向位移、时间等数据,并保存为Excel 形式文件。

1.2 试验结果

图3为3 种粒径玻璃微珠轴向应变随时间变化曲线。由图3可知,随着轴向荷载的增加,玻璃微珠轴向变形呈现逐渐增大的趋势。对同一粒径玻璃微珠,每级加载初始阶段,轴向应变增长较快,而后增长趋势逐渐变缓。不同粒径的玻璃微珠在相同荷载下的轴向应变有明显的差异:在1 MPa时,各个粒径玻璃微珠的轴向应变曲线非常接近,随着荷载的逐级增加,不同粒径玻璃微珠的轴向应变差异性增大;在5 MPa 时,2.0～2.5 mm 粒径的玻璃微珠轴向应变为0.026 mm,0.6～0.8 mm 的轴向应变为0.009 mm。

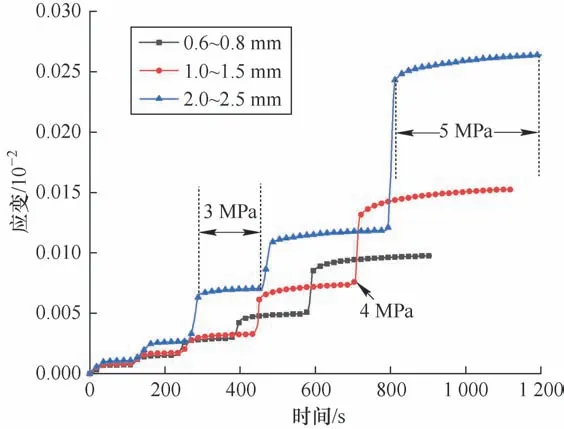
图3 玻璃微珠应变-时间曲线Fig.3 Strain-time curves of glass bead

1.3 陈氏叠加法

陈氏法叠加原理是由陈宗基于1964年率先提出的,经过其学生的研究发展,目前已经成为处理岩石这种非线性材料蠕变试验数据的常用手段。陈氏法的优点在于,它通过作图能够描述岩石等材料变形过程中真实的叠加关系。陈氏法处理蠕变试验如图4所示。

图4 陈氏法处理蠕变试验数据Fig.4 Chen's method of processing creep test

陈氏叠加法首先假定对岩石材料进行了级距为Δσ 的分级加载试验。若岩石材料在第一级荷载的条件下,经过时间t1达到了稳定蠕变状态,其蠕变曲线将继续沿着图中虚线,按照一定斜率继续延伸。施加第二级荷载对岩石材料产生的变形,为图中第二级荷载蠕变曲线与虚线之间的区域,将此变形叠加到第一级荷载下的蠕变曲线上,便得到了第二级荷载下的蠕变曲线。以此类推,分别得到了每一级荷载下的蠕变曲线。

依据陈氏法叠加原理处理分级加载试验数据,绘制3 种粒径玻璃微珠颗粒在不同应力下的应变-时间曲线,如图5所示。

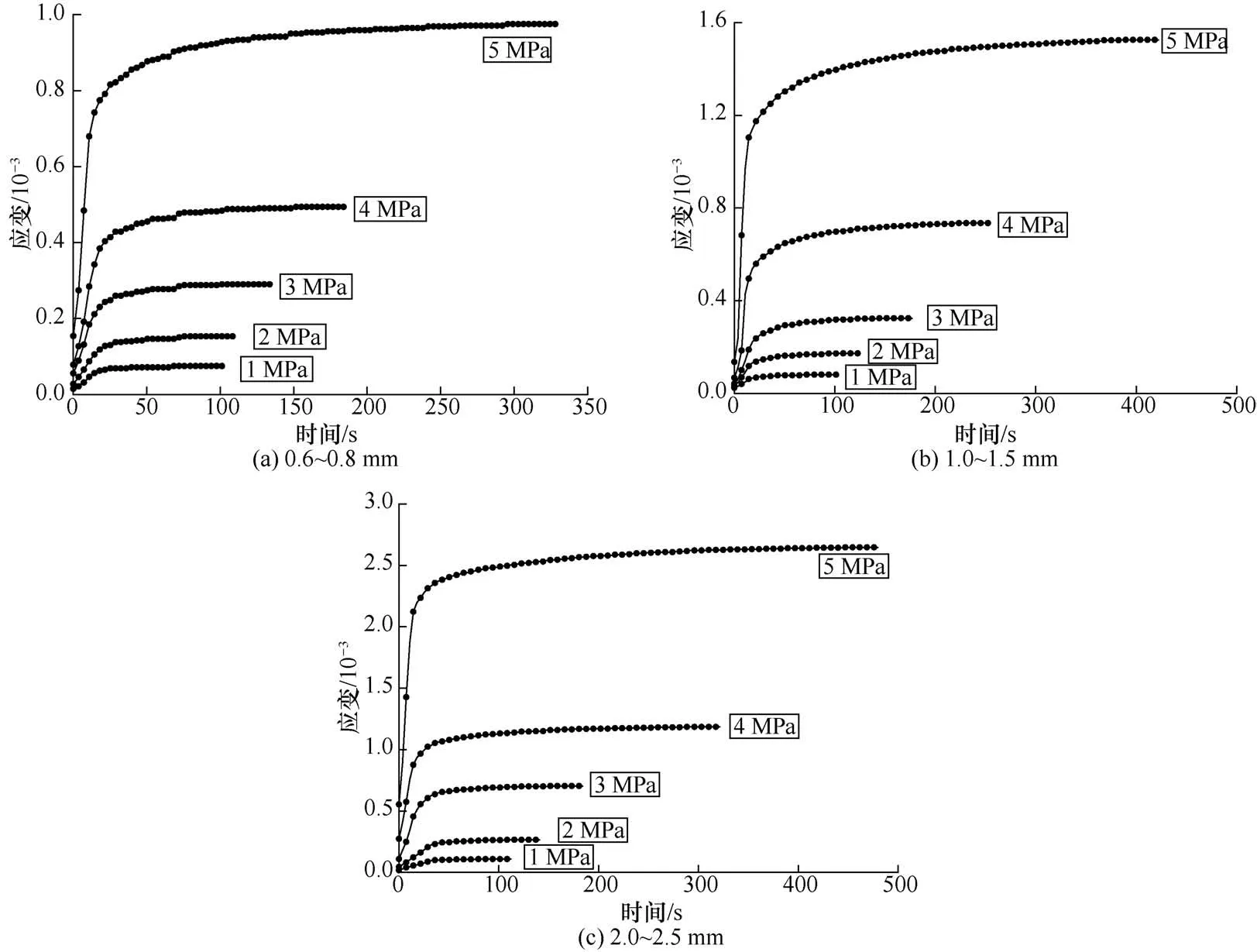
图5 不同粒径的应变-时间曲线Fig.5 Strain-stress curves of glass bead with different particle sizes

2 颗粒堆积体蠕变模型研究

2.1 Burgers 蠕变模型

对于岩石颗粒的蠕变模型,学者们多用组合元件模型进行分析,常见的组合模型有Maxwell 模型、Kelvin 模型、Burgers 模型和西原模型等。在加载试验中,不同粒径的岩石颗粒堆积体出现了较明显的初始蠕变、衰减蠕变和稳定蠕变阶段,而Burgers 模型能够准确地反映岩石颗粒堆积体在衰减蠕变和稳定蠕变阶段的变形特征,对于玻璃微珠这类非晶体聚合物,它也可以很好地表示非晶体黏弹行为的基本特征。本文选用Burgers 模型,由一个Maxwell 体和一个Kelvin 体串联而成的,其中Maxwell 体由一个弹性元件和一个黏性元件串联而成,而Kelvin 体由弹性元件和一个黏性元件并联而成,具体结构如图6所示。

图6 Burgers 模型结构示意图Fig.6 Schematic diagram of the Burgers model

Burgers 蠕变方程为

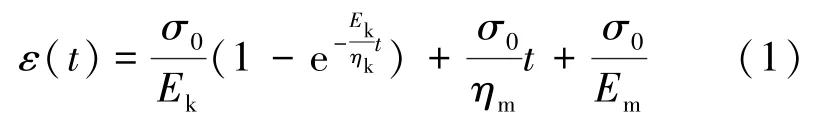
式中,ε(t)为任意时刻下的蠕变值;σ0为轴向偏应力;Ek和ηk分别为Kelvin 弹性系数和黏性系数;Em和ηm分别为Maxwell 弹性系数和黏性系数。

通过拟合确定了Burgers 模型4 个参数Ek、Em、ηk、ηm的取值,通过相关系数R2来评价Burgers 模型的拟合程度,R2越接近1,说明Burgers模型拟合的程度越好,具体见表1。

表1 Burgers 蠕变模型参数统计Table 1 Parameter statistics of burgers creep model

图7为不同粒径Burgers 蠕变模型拟合曲线。由图7可知,通过Burgers 模型得到的拟合曲线与实测曲线对比,3 种粒径的玻璃微珠颗粒的拟合效果均很理想,R2都在0.96 以上,说明Burgers 模型能够准确地反映玻璃微珠在恒载状态下的蠕变特性。

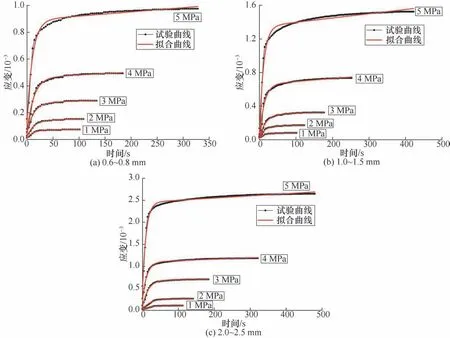
图7 不同粒径Burgers 蠕变模型拟合曲线Fig.7 Fitting curve of burgers creep model with different particle sizes

2.2 Burgers 模型4 参数分析

一些学者研究了Burgers 模型参数对岩石蠕变特性的影响,认为Em反映岩石试样加载瞬间的变形量,Ek反映岩石试样在衰减蠕变阶段的最终变形量,ηm反映岩石试样在稳定蠕变阶段的变形速率,ηk反映岩石试样在衰减蠕变阶段的变形速率。

由图8可知,Kelvin 弹性系数Ek、Maxwell 体弹性系数Em、Kelvin 体黏性系数ηk和Maxwell 体黏性系数ηm随着轴向应力和粒径都呈现负相关的关系。Kelvin 弹性系数Ek反映岩石试样在衰减蠕变阶段的最终变形量,主要是由于粒径大,颗粒堆积体空隙率大,小颗粒填充在空隙中,在相同的荷载下,大粒径颗粒的最终变形量越大。Maxwell 体弹性系数Em反映岩石试样加载瞬间的变形量,由于颗粒加载初期,2.0～2.5 mm 颗粒空隙大,小颗粒可以快速填充到大的空隙中,导致在加载初期大颗粒的变形量大。Kelvin 体黏性系数ηk反映岩石试样在衰减蠕变阶段的变形速率,加载初期,黏性系数ηk下降缓慢,随着轴压的增大,下降的速率逐渐增大,主要是由于在蠕变衰减阶段,加载初期的压力较小,不足以克服颗粒之间的咬合力,随着轴压的增大,颗粒之间的稳定结构被破坏。Maxwell黏性系数ηm反映岩石试样在稳定蠕变阶段的变形速率,加载初期,黏性系数ηm下降的较快,随着轴压的增大,下降的速率逐渐降低。粒径与黏性系数ηm也呈负相关关系,主要是由于粒径小的试样空隙率小,颗粒之间接触紧密,咬合力强,颗粒之间难以滑动与滚动,导致粒径小的试样比大粒径有更高的黏性系数。

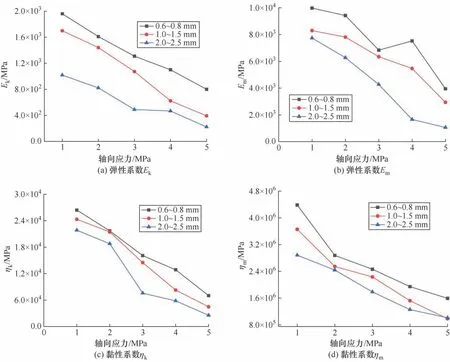
图8 不同粒径Burgers 模型4 参数在加载过程中变化曲线Fig.8 Variation curves of four parameters of Burgers model with different particle sizes during loading

3 基于颗粒流的细观蠕变数值分析

颗粒堆积体是特殊的散体材料,粒间黏结强度十分小,基于有限元方法的连续性假设局限于对堆石料宏观力学性能上的研究,并不能精确反映颗粒细观结构对宏观力学行为造成的影响。因此,从细观层面,采用离散元颗粒流程序进行分析,弥补了传统有限元的缺点,是目前运用最为广泛和成熟的数值模拟软件。

根据室内试验实际情况,建立3 种粒径的二维数值模型,模型直径25 mm,高度h=80 mm,如图9所示。

图9 二维离散元数值模型Fig.9 Two dimensional discrete element numerical model

颗粒之间接触用Burgers 蠕变模型,相比于宏观力学中的Burgers 蠕变模型,PFC 中Burgers 接触模型(图10)善于分析法向接触和切向接触的受力状态。

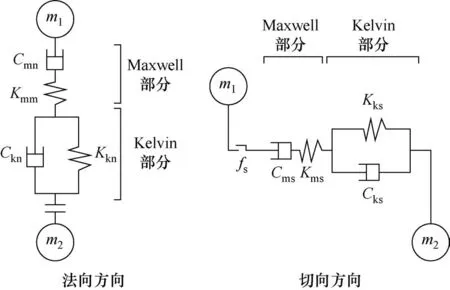
图10 Burgers 蠕变接触模型Fig.10 Burgers creep contact model

在该模型中,Maxwell 体和Kelvin 体在接触的法向方向和切向方向上均起作用。除此之外,在接触的法向方向上,由Maxwell 体和Kelvin 体串联而成的结构还包括了一个无张力组件,作用是描述颗粒间的线弹性摩擦行为;而在接触的切向和法向上,由Maxwell 体和Kelvin 体串联而成的结构还包括了一个滑动器,作用是判别颗粒之间发生滑动的条件是否满足库伦定律。所以,对于颗粒流程序中Burgers 蠕变模型的9 个参数为法向的Cmn、Kmn、Ckn、Kkn,切向的Cms、Kms、Cks、Kks以及摩擦系数fs,根据文献[22-24]研究成果,将试验拟合得到的宏观Burgers 模型参数转换为颗粒流程序中的微观Burgers 模型参数,其计算公式见式(2)至式(9)。

式中,L为相邻岩石颗粒之间球心距;υ为泊松比,本文取0.25。

选择轴压为5 MPa 进行蠕变数值计算,根据式(2)至式(9)分别计算不同工况下数值模型的Burgers 模型细观参数,并输入到程序中,不断进行程序试运算,对模型的摩擦系数、与墙体接触刚度以及阻尼等参数进行调试,直到得到最优的模拟曲线。不同工况下数值模型的Burgers 模型细观参数见表4。

表4 不同粒径Burgers 模型细观参数Table 4 Meso parameters of Burgers model with different particle sizes

通过颗粒流数值模拟方法得到了上述3 种粒径颗粒加载条件下的应变随时间的变化曲线和应变值对比,如图11和表5所示。

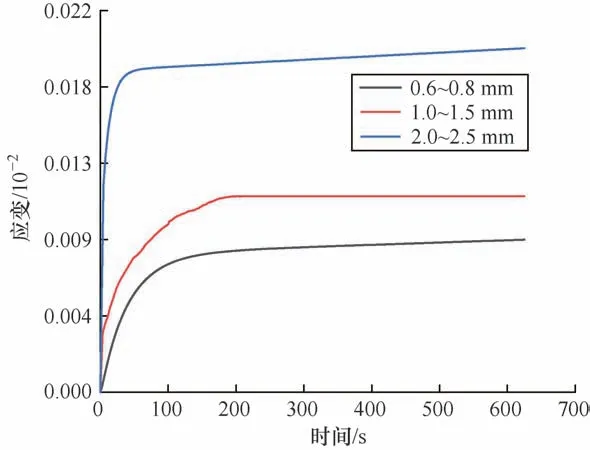
图11 3 种粒径数值模拟曲线结果Fig.11 umerical simulation curve results of three particle sizes

表5 数值模拟与试验稳定蠕变阶段应变值对比Table 5 omparison of strain values between single particle size simulation and test stable creep stage

由图11可知,利用PFC2D5.0 实现了岩石颗粒二维离散元虚拟双轴蠕变试验,模拟蠕变曲线与试验曲线趋势大体一致,均呈现初始蠕变、减速蠕变以及稳定蠕变阶段,通过与试验稳定蠕变阶段应变值进行对比,模拟的应变值略小于试验值,该模型可以用来模拟岩石颗粒蠕变试验。

4 结 论

(1) 通过Burgers 模型得到的拟合曲线与实测曲线对比,3 种粒径的玻璃微珠颗粒的拟合效果均很理想,Burgers 模型能够准确地反映玻璃微珠在恒载状态下的蠕变特性。

(2) Burgers 模型的4 参数Ek、Em、ηk、ηm随着轴向应力和粒径均呈现负相关的关系。颗粒粒径与Burgers 模型的参数关系密切,通过影响Burgers模型4 个参数,进而影响堆积体的蠕变特性。

(3) 使用颗粒流软件PFC2D建立与实验室试验相对应的数值计算模型,实现宏观Burgers 模型参数到微观参数之间的转换,可以对实验室试验结果进行验证。