冰川模型及其在古冰川模拟研究中的应用

2022-09-15李英奎杨玮琳许向科

冰川冻土 2022年4期

李英奎，杨玮琳，陈鑫，刘强，许向科

（1.Department of Geography，University of Tennessee，Knoxville，TN 37996，USA；2.北京大学城市与环境学院，北京 100871；3.河北师范大学地理科学学院，河北石家庄 050024；4.中国科学院青藏高原研究所，北京 100101）

0 引言

冰川约占全球淡水资源的70%，是全球水循环和冰冻圈的重要组成部分。在全球尺度上，冰川变化可以影响海平面升降、洋流乃至大气环流格局［1-2］。在区域尺度上，冰川是诸多大江大河的发源地，与区域水资源、生态系统和人类栖息环境密切相关［3］。进入21世纪以来，随着全球温度的持续暖化，南北极冰盖和山地冰川的消融速度不断加快，冰川覆盖范围明显缩小［4］。青藏高原是全球除两极外冰川覆盖最多的地区，有“第三极”［5］和“亚洲水塔”之称［6］。近年来青藏高原的冰川主体处于退缩状态［7-9］，冰川面积持续减少，厚度不断减薄［10-11］，对该地区的水资源造成重要影响，使“亚洲水塔”逐渐朝着失稳方向发展［5，12-14］。

冰川变化与温度和降水变化密切相关，也被称为“大陆温度计”［15］。冰川本身由于长时间的积累记录了万年甚至十万年以来的气候变化，冰芯的研究可以恢复高分辨率的古温度和降水变化，如古里雅冰芯记录了过去13万年的气候变化信息等［16］。另外，冰川变化也留下了丰富的地貌遗迹［15，17］，这些冰川地貌遗迹是过去冰冻圈变化的最直接证据，蕴含了丰富的气候信息，能够有效恢复古冰川的时空作用范围和规模，探究冰川变化的气候驱动机制［18-20］，对合理预测未来冰川变化及其环境影响提供可靠依据［21］。

近年来，随着测年技术尤其是宇成核素暴露年龄和光释光等方法的不断发展，对很多地区的冰川地貌都实现了直接测年，将冰川地貌研究推进到定量分析阶段［17］。例如：仅在青藏高原地区就已经积累了上千个冰川地貌年代数据，大大促进了对该地区古冰川演化的认识和理解［15，17，22-29］。同时，随着高分辨率影像、数字高程模型（DEM）和地理信息系统（GIS）的快速发展，冰川地貌制图技术也逐渐细化和完善，可以实现对古冰川范围及平衡线高度（Equilibrium-line altitude，ELA）等参数的大范围恢复和计算，为深入探讨古冰川的时空变化规律和气候驱动机制奠定基础［30-42］。然而，由于冰川地貌记录的不完整性和测年误差等因素，区域冰川演化及古冰川地貌的识别、解译和制图研究中还存在很多不确定性［43-44］。

冰川模型能够模拟冰川在不同条件下的物理特征［45-47］。由于该模型需要较为详细的气候数据，其主要用于气候资料较丰富的未来冰川变化预测。随着古气候和古冰川年代、范围研究的不断深入，目前已有与古冰川变化相关的冰川模拟研究，尤其是在观测数据比较多的地区，如：格陵兰冰盖［48］、南极冰盖［49-50］和欧洲阿尔卑斯山［51-52］等地区。冰川模型也逐渐用于青藏高原地区古冰川的模拟和古气候恢复。目前较多的研究包括使用一维冰川剖面形态模型结合降水-温度经验关系重建冰川发育不同时期的古气候［53］，以及采用二维（2-D）冰流模型模拟不同时期冰川达到稳态的厚度、体积以及所需的气候条件等［18，54-62］。也有一些研究开始使用比较连续的古气候资料模拟区域历史时期冰川的连续变化［40-41，63-66］。与传统地貌学根据冰川地貌特征推测古冰川演化和古气候特征的研究不同，冰川模型能够更加深入地探讨冰川对气候的响应机制及区域差异，量化古气候特征，为冰川未来变化预测提供理论基础［19，53］。尽管冰川模型在古冰川恢复和古气候重建方面存在很大潜力，但其在实际应用中仍存在很多问题，尤其是对山地冰川的模拟，比如用于多数冰川模型的浅冰近似方法（Shallow Ice Ap⁃proximation，SIA）在物理机制上并不完全适用于山地冰川的模拟等。另外现有研究利用冰川模型模拟单一或几条冰川变化时比较可行［58，60，67］，但在模拟大范围冰川变化时存在与野外观测的地貌特征和年代学证据不符等问题［68］。这说明冰川模型使用的气候、地形等驱动因子存在不足，不能简单利用现有的冰川驱动因子模拟古冰川变化。另外，冰川模拟结果与观测的冰川地貌还多停留在简单的目视对比阶段，缺乏定量的评估方法。

本文简述现有不同冰川模型对古冰川模拟的方法和原理，总结这些模型在古冰川模拟和古气候重建中的应用，探讨现有研究中存在的问题和未来发展趋势。这一综述将进一步加强和改进冰川模型在古冰川模拟研究中的应用，对恢复古冰川的规模、演化过程及其气候驱动机制具有重要意义，为深入理解未来冰川变化特征、机理和影响奠定基础。

1 冰川模型综述

1.1 地貌-冰面剖面形态模型

地貌-冰面剖面形态模型根据能够指示古冰川边界（如冰碛垄等）和高度（如trimline等）的地貌结合基于冰川物理学原理的冰面剖面形态（Ice Sur⁃face Profile）恢复古冰川特征，如厚度、范围、体积等［69-72］。该模型假设在一定的地形条件下，冰川达到稳定状态，即冰川的厚度、宽度和坡度不随时间发生变化，冰川的厚度分布由剪切应力引起。在理想塑性体条件下，冰体所受的剪切应力在冰川底部达到最大［69］［式（1）］：

式中：H为冰的厚度（m）；h为冰川表面海拔（m）；x为水平坐标（m）；ρ是冰密度（900 kg·m-3）；g是重力加速度（9.81 m·s-2）；α为冰表面坡度（rad）；τr为基底剪切应力（kPa）。这个公式表明对于特定的冰川剪切应力，冰面坡度与冰川厚度成反比。因此，根据野外观测的冰川地貌所指示的古冰川末端（如终碛垄）、局部边界（如侧碛垄）或高度（如trimline）等信息，利用上述理想塑性体的冰面剖面形态，可以恢复整个古冰川的范围和厚度。野外观测和实验模拟结果显示，山谷冰川的剪切应力通常在50～150 kPa范围内［70-71］，冰斗冰川的基底剪切应力较大，约为190 kPa［72］。在冰川反演模型中，通常取τr为100 kPa［73］。

除基底剪应力外，山地冰川的流变也受到谷地地形影响。如由于冰川坡度和厚度的空间变化，冰体会受到拉伸或压缩应力，造成基底剪应力的空间差异。Nye［69，74］提出可以通过冰川横截面，即冰川谷形态指数（f）矫正基底剪切应力。该指数取决于横截面形状，与冰川横截面面积、冰底周长和冰川横截面最大厚度有关［式（2）］：

式中：A为冰川横截面积（m2）；p为冰底周长（m）；H为冰川横截面最大厚度（m）。矫正后的基底剪切应力为τr/f。另外，Li等［75］提供了一种利用多项函数拟合提取冰川横截面有效宽度来计算f因子的方法。

地貌-冰面剖面形态模型首先根据理想塑性体假设和反映冰川边界和高度的地貌约束求解冰川流线上的冰厚，然后通过空间插值计算其他区域的冰川厚度。Benn等［76］开发了一个简单的ExcelTM计算程序进行冰川流线模拟。Pellitero等［73］进一步将该模型改写为可视化的ArcGIS工具包（GlaRe），使其能在ArcGIS中恢复古冰川的范围、厚度、体积和表面地形。James等［77］编写了Volume and Topogra⁃phy Automation（VOLTA）模型用于冰川厚度的模拟。然而，这些模型尚需要大量的手工绘制冰川流线和参数调整才能对一个地区的古冰川变化进行模拟。李英奎在集成VOLTA的冰川中流线和冰厚模型、古冰川纵剖线模型和GlaRe模型的基础上，增加了冰川流线自动提取和参数自动调整等模块，编写了基于ArcGIS进行古冰川厚度和体积模拟的PaleoIce模型（尚未发表）。这一模型需要DEM、冰川轮廓或特定位置的冰川边界等信息重建古冰川的厚度和体积。模型具有自动生成现代冰川及古冰川的中流线、自动计算冰川谷形态指数（f）和基底剪应力、自动模拟冰川厚度、体积和冰面地形等功能。图1给出了根据PaleoIce模型重建冰川厚度和冰面地形的基本流程［78］。

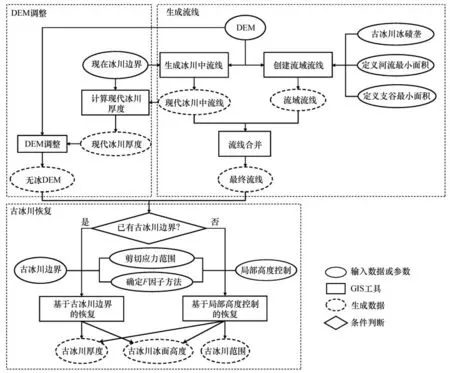
图1 利用地貌-冰面剖面形态模型PaleoIce恢复古冰川的示意流程图（根据赵晓艳等［78］修改）Fig.1 An example of the flowchart of the paleoglacier reconstruction using the landform-ice surface profile model，PaleoIce（modified from Zhao et al［78］）

王潍诚等［79］比较了中国西部14条山地冰川的雷达测厚和根据理论计算的冰面剖面数据，通过实测数据与不同底部剪切应力得到的剖面数据的拟合，得到中国西部山地冰川的底部剪切应力介于33～126 kPa之间。赵晓艳等［78］利用改进的地貌-冰面剖面形态模型PaleoIce（图1）对念青唐古拉山的扎当冰川进行了模拟并与雷达测厚数据对比，评估了四种DEM数据（ALOS PALSAR RTC HIGH RES 12-m、ASTER GDEM 30-m、SRTM 30-m DEM、SRTM 90-m DEM）对冰川模拟的影响，结果表明不同类型和分辨率DEM模拟的冰川厚度与雷达测厚数据的平均误差为-8.7%～10.3%，其中SRTM 30 m DEM模拟的冰川平均厚度误差仅为-0.5%。虽然这些研究只对比了现代冰川的雷达测厚数据，但也在一定程度上说明利用这一模型进行古冰川模拟的可靠性。

1.2 物质平衡-冰川动力耦合模型

物质平衡-冰川动力耦合模型根据能量-物质平衡关系和冰川动力学原理模拟冰川变化。与地貌-剖面形态模型不同，这一模型实现了物质平衡与冰川动力模块的耦合，首先通过能量-物质平衡确定冰川的物质平衡变化，然后以此驱动冰川动力模块模拟冰川变化［80-81］。使用物质平衡-冰川动力耦合模型进行古冰川的模拟主要包括两种方式：一种方式通过长时间连续的气候或物质平衡数据模拟古冰川的动态变化过程，称为连续模拟［41，64］。另一种方式仅模拟冰川在一定气候或物质平衡条件下达到稳定状态的大小和规模，称为稳态模拟［40］。物质平衡-冰川动力耦合模型由于存在大量的参数，需要使用实测气候和物质平衡数据进行参数校验和调整。同时，模拟结果也可以与冰川地貌进行对比，进一步调整模型参数，提高模拟精度。物质平衡-冰川动力耦合模型的优势在于能够把冰川变化与气候驱动条件结合，对理解古冰川变化的气候驱动机制和估算古冰川发育时期的气候信息具有重要价值。

1.2.1 冰川能量-物质平衡模块

冰川能量-物质平衡模块主要包括三种形式：基于物理过程的能量平衡模型、基于经验统计的温度指数模型，以及基于冰川平衡线（ELA）的经验模型［20，57-58，81-82］。

能量平衡模型（energy and mass balance model，EMB模型）基于能量平衡原理计算冰川表面能量收支的不同分量，获取冰川的消融量［81，83-86］。能量平衡具体可用式（3）表示：

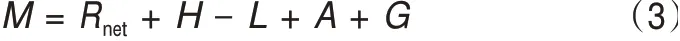
式中：M为冰雪融化消耗的能量；Rnet为净辐射或辐射平衡量；H为感热交换量；L为潜热交换量即蒸发/升华消耗的能量。A和G分别为液态降水冻结释放的热量和地表下的热通量。由于这两个量的数值一般远小于其他量，因此在计算中通常忽略不计［87-88］。能量平衡模型有比较扎实的物理学基础，因此在理论上相对完善。但由于该模型需要大量的实测数据，在实际应用中存在局限性和不确定性。

温度指数模型基于冰面消融和气温的经验统计关系确定冰川物质平衡［89-93］。一般而言，冰川物质平衡是冰川积累量与消融量之间的平衡，冰川积累取决于固态降水量，而气温（高于临界温度，如：0℃）决定冰川的消融量。温度指数模型所需参数较少，经验关系也比较容易确定，因此目前已被广泛用于古冰川的模拟［80，94-95］。度日模型（Degree-Day Model，DDM）是最常见的一种温度指数模型［式（4）］：

式中：SMBz为高度z的冰川物质平衡量（mm·a-1）；Pz为高度z处的月平均累积固态降水量（mm，通常根据月累积降水量乘以一个修正因子求得）；T+z为高度z处冰川的正积温（℃）；DDF为度日因子（Degreeday factor；mm·d-1·℃-1）。这一因子在不同地区的变化较大，如：已有研究表明中国西部冰川的度日因子有很大的空间分异，变化于2.6～13.8 mm·d-1·℃-1之间［96］。

一些地区冰川的物质平衡关系与冰川平衡线（ELA）相关，如：Caidong等［97］在模拟念青唐古拉山西部冰川时，发现冰川ELA和SMB存在一定的线性关系［式（5）］。

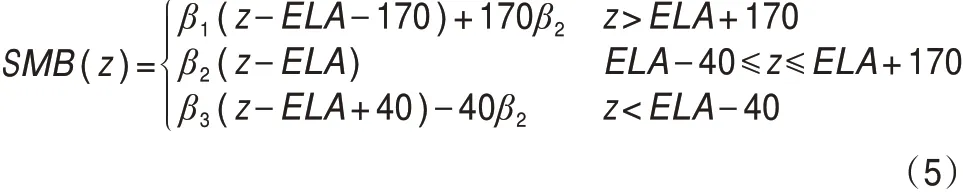
式中：β1、β2和β3分别为0.6、13和5 mm·a-1。这种物质平衡与ELA的经验关系可以大大简化冰川的模拟。目前，已有研究根据这一经验关系计算冰川物质平衡，驱动动力模块，模拟念青唐古拉山的古冰川变化［57］。

1.2.2 冰川动力模块

冰川动力学的模拟一般采用塑性流体假设，使用质量守恒方程、动量守恒方程组（Navier-Stokes方程组）、本构方程（Glen定律）以及物理方程（或称为几何方程）模拟冰川变化［3］。考虑模型的维度，冰川动力模块可以分为一维、二维和三维模型。由于冰川动力模块较为复杂，涉及的公式和变量较多，下面以Plummer等［81］开发的二维平面冰流模型为例，着重介绍二维平面冰川动力模块的原理，然后简述一维和三维模型与二维模型的差异。二维平面冰流模型对与冰川动力相关的方程组做了一定程度的简化和近似。如在质量守恒方程中，将冰川视为块体，仅考虑了水平面上沿x和y方向的冰通量变化（qx和qy；m2·s-1）而忽略了垂直z方向的冰通量变化［式（6）］。

冰通量由冰川厚度和冰川运动速度（u）共同决定。假设冰流速矢量与冰川表面平行（层流假设），根据冰流速与应变率的关系（几何方程）和冰的流动定律（Glen定律），可得出冰川运动速度（u）由冰川内部变形速度（ud）和底部滑动速度（us）组成［式（7）］：

式中：A根据冰蠕变参数求得（1×10-7Pa-3·a-1）；B根据冰滑动参数求得（1.5×10-3m·Pa-3·a-1）；m=3和n=2根据Glen定律的指数求得；f为调节冰川变形和滑动速度占冰流速比例的参数，通常取f=0.5。

根据冰川模型中比较通用的浅冰近似（Shal⁃low Ice Approximation），动量守恒方程组可进一步简化，式（8）为简化后的基底剪切应力τ：

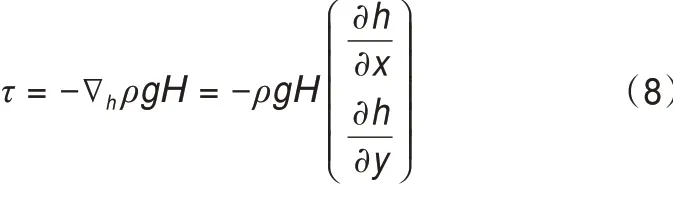
式中：∇h为二维哈密顿算子。目前以Plummer等［81］为代表的二维冰流模型多采用稳态模拟进行不同地区的古冰川模拟和冰川发育时期的古气候参数估算［18-19，54-62］。

与二维平面冰流模型相比，一维冰川动力模型仅考虑通过冰川流向某一横截面的冰通量［q；式（9）］：

式中：S为流线上某一个横截面的面积（m2）。在动量守恒中也只有一个方向的剪切应力为非零应力分量。一维冰川动力模型以Maussion等［80］开发的OGGM模型为代表。由于其运行效率及空间分辨率比二维和三维模型更高，被广泛用于区域乃至全球的冰川变化模拟［98-101］。

三维冰川动力模型进一步考虑垂直z方向的运动对冰川动力和质量守恒的影响。目前，应用比较广泛的三维冰川动力模型包括基于浅冰近似的PISM模型［40-41，48-52，64］、GLIMMER模型［101］、SICOPO⁃LIS模型［102-103］，和基于Navier-Stokes方程构造的El⁃mer/Ice模型［106-107］等。

Farinotti等［108］利用全球21个测试地区的冰川实测数据评估了17个冰川厚度模型的有效性。其中使用的很多冰川厚度模型都基于前面讨论的冰川动力学方程。结果表明，尽管不同模型在冰川厚度模拟上存在不少差异，但多个模型的平均与实测平均冰厚的差异可以控制在（10±24）%（1个标准差）之内，证明了冰川动力模型在冰川模拟研究中的有效性。

1.2.3 模型参数的校验

物质平衡-冰川动力耦合模型通常具有很多参数，需要根据冰川观测数据调整和校验模型参数。在具体应用中一般采用具有长期观察的冰川物质平衡和过去历史时期的气候数据，利用不同冰川参数模拟过去历史时期的冰川变化，并与现代冰川进行对比，得到与之符合最好的参数，然后使用这些参数模拟冰川的变化。对于古冰川的模拟，由于存在大量不同期次的野外地貌数据，冰川模拟结果也可以与这些地貌数据进行对比，进一步调整模型参数，提高模拟精度。然而，目前大多数冰川模拟的参数校验还局限于简单的目视对比，缺乏定量的评估。近年来，随着GIS技术的发展，一些定量评估冰川模型与冰川地貌符合度的研究也逐渐发展和完善。

冰川模拟的结果可以从冰川边界、高程以及流线等不同角度进行校验。如果冰川各个方向的边界（现代冰川或冰川地貌）都比较清晰，冰川边界可以用面状多边形进行表示。这种情况可以使用多边形叠加或栅格数据叠加的方法进行精度校验（后者类似于影像分类精度分析）。多边形叠加方法可以得到两者重叠部分占总区域的百分比［109-110］［式（10）］：

式中：C1和C2是冰川模拟的边界多边形和地貌边界多边形，∩和∪是多边形交运算（Intersection）和并运算（Union）分析。重叠度100%代表两者完全一致，低的百分比代表两者重叠度较小，模拟精度低［109-110］。

如果冰川边界只在局部区域清晰，其只能通过局部边界线的方式表示。这种情况不能通过上述多边形叠加的方法评估冰川模拟边界与地貌边界的符合程度。Napieralski等［111］提出了Automated Proximity and Conformity Analysis（APCA）方法比较两个线性边界的接近和一致程度。Li等［112］进一步改进和提出了Revised Automated Proximity and Conformity Analysis（R-APCA）方法。如图2所示，R-APCA计算两个线性边界的平均距离，用于描述它们的接近程度（proximity），同时计算两个线性边界不同位置距离的方差，用于描述两者的一致程度（conformity）。如果两个边界具有最小平均距离和方差，则二者符合程度最好。这一方法已经用于大陆冰盖模拟结果的评估［113］。

图2 改进的Automated Proximity and Conformity Analysis（根据Li等［112］修改）：四个假设的冰川地貌边界基本平行于冰川模型边界的情况（a）；四个假设的冰川地貌边界与冰川模型边界具有不同旋转角度的情况（b）；对于情况（a），不同冰川地貌边界与冰川模拟边界具有不同的平均距离，但相似的方差（c）；对于情况（b），不同冰川地貌边界与冰川模拟边界具有相似的平均距离，但不同的方差（d）Fig.2 Revised APCA analysis（modified from Li et al［112］）：four parallel linear field features compared with a model-predicted ice margin（a）；four linear field features with different angles of rotations compared with model output（b）；for parallel shift scenarios（a），four linear features show distinctly different mean offsets but similar standard deviations（c）；for rotation scenarios（b），different features represent different standard deviations with similar mean distances（d）

一些冰川地貌也能够用来恢复冰川的流向，如鼓丘、羊背石、鲸背岩、基岩磨光面擦痕等。山地冰川由于受到谷地的限制，冰川流向一般与谷地方向一致。大陆冰盖和冰帽等冰川流向可以不完全受谷地地形控制。因此冰川流向的地貌证据可以作为校验冰川模型的一个重要指标，尤其是对冰盖和冰帽等的模拟。Li等［114］提出和开发了基于流向对比的模拟校验方法（Automated Flow Di⁃rection Analysis，AFDA），具体为计算冰川模拟流向与实测冰川流向的角度差异。由于冰川流向是角度变量，角度差异不能使用简单的均值和方差计算，而是计算二者的Vector-mean和Vectorstrength（图3）［114］。

图3 自动流线对比分析方法（根据Li等［114］修改）：野外实测的冰川流线与冰川模拟的流线（栅格格式表达）（a）；将实测流线与模拟流线在不同模拟时段进行栅格叠加（b）；不同时段冰川模拟流线与实测流线的平均角度差异变化（c）；选取的两个特定时段模拟流向与实测流向的角度差异变化分布（d）Fig.3 AFDA analysis（modified from Li et al［114］）：field-based glacial lineations and model outputs used in the analysis（a）；overlay model outputs and field evidence to produce a series of residual datasets for different time slices（b）；plot resultant mean of residuals against their corresponding time slices to identify temporal patterns of correspondence between predicted directions and field observations（c）；frequency analysis（rose diagram）of selected time slices（e.g.d and f）provides detail information on distribution of residuals across area and can be used to evaluate level of correspondence（d）

古冰川的厚度或高度一般比较难确定，但有时可以通过trimline、残余岩丘（tor）等确定一些局部地区的冰川高度，或者冰川不可能达到的高度极限。这些关于高度和厚度的信息也可以用来校验冰川模型参数。由于这些局部地点多为点状分布，可以通过高程点的对比及线性回归等方法进行校验。如果野外观测的高程点可以连成比较连续的线，也可以把这些连线视为冰川边界，使用前面提到的APCA或R-APCA等边界对比方法进行模拟结果比较和模型参数校验。

1.3 不同冰川模型和模拟方式的对比和适用性

表1列出了两类冰川模型以及物质平衡-冰川动力耦合模型的两种模拟方式所需要的模型运行的必要输入、提高模拟精度的可选输入（用于参数校验）和模型输出数据等，并总结了不同模型或模拟方式的优缺点。总体而言，地貌-冰面剖面形态模型相对简单，所需输入数据和参数不多且容易获得，比较容易掌握和应用。但模型本身与影响冰川发育的气候因素没有关联，不能直接用来恢复冰川发育时期的古气候信息。对古气候信息的恢复需要借助其他方法间接获取，详见2.2节。

表1 不同冰川模型和模拟方式在古冰川模拟方面的比较Table 1 Comparison of different models and modelling strategies in paleo-glacial simulation

物质平衡-冰川动力耦合模型需要物质平衡和气候驱动数据进行模拟。由于很多地区缺乏这类数据，因此，该模型在一些区域上的应用存在局限性。但该模型本身实现了冰川运动与其气候驱动因素的耦合，能够直接获得冰川发育时期的古气候特征。针对这类模型的两种模拟方式而言，稳态模拟相对简单，对古气候数据的要求不高，只需要提供不同的ΔT-ΔP组合。连续模拟需要提供长时间的连续古气候数据，所需计算资源也较多，在冰川模拟中尚处于起步阶段。

2 冰川模型在古冰川模拟研究中的应用

2.1 恢复古冰川的范围、体积、平衡线等参数

地貌-冰面剖面形态模型根据地貌边界和局部高度等信息求解冰川流线上的厚度和表面高度，并进一步插值其他区域冰川厚度、表面高度以及冰川面积和体积等参数。由于地貌-冰面剖面形态模型中不包括物质平衡模块，因此不能直接确定冰川平衡线（ELA）。在这种情况下，可以根据地貌学方法利用恢复的古冰川范围和表面高度间接估算ELA。具体包括积累区面积比率法（accumulation area ra⁃tios，AAR）、冰川末端至冰斗后壁比率法（toe-toheadwall altitude ratio，THAR）、面积高度平衡比率法（area-altitude balance ratios，AABR）、赫斯法（Hess）等［82，115-116］。其中，AAR法是相对使用最多的方法。AAR法假设冰川处于稳态时，冰川积累区占整个冰川的面积比例固定。较大规模的冰碛垄需要较长的堆积过程，一般都是冰川处于稳态时形成的，符合AAR法对稳态冰川的假设。通常，中高纬度冰川的AAR值一般介于0.5～0.8之间［117］，冰斗和山谷冰川的AAR值为0.6±0.05［117］，中国西部山地冰川的AAR值平均为0.71左右［118］。

根据地貌法估算古冰川ELA的研究大多只是依据古冰川地区的地形特征。由于这些地形大多形成于冰川退缩之后，并不代表古冰川的表面地形。研究表明，根据冰面和冰底地形恢复的ELA具有较大的差异［53，77，119-121］。因此，恢复冰川厚度/冰面高度分布是估算古冰川ELA及其变化的必要步骤。目前，地貌-冰面剖面形态模型已应用于恢复古冰川厚度、体积和冰面高度变化，并进一步恢复ELA等参数［119-120，122-124］。此外，由于存在不同分辨率和精度的DEM，不同DEM对古冰川的恢复也存在差异。赵晓艳等［78］评估了四种不同的DEM（ALOS PAL⁃SAR RTC HIGH RES 12-m、ASTER GDEM 30-m、SRTM 30-m DEM、SRTM 90-m DEM）对恢复青藏高原卡若拉垭口地区不同冰期冰川面积、体积、厚度和ELA等参数的影响，发现冰川对高分辨率的细微高程变化可能并不敏感，同时分辨率过低的DEM可能过分简化冰川变化的地形因素。因此过高或过低的DEM分辨率都可能造成冰川模拟结果与实测数据的差异。结果显示SRTM 30-m DEM与其他DEM相比能更好地模拟古冰川变化。另外，不同

DEM对于古冰川面积和ELA的恢复影响较小，对体积的影响较大。同时，不同DEM对恢复古冰川的影响与冰川规模有关，从现代冰川到末次冰盛期冰川，随着冰川面积增大，不同DEM对冰川参数恢复的影响逐渐减少，恢复的古冰川参数变化趋于稳定［78］。

物质平衡-冰川动力耦合模型可通过稳态模拟方式恢复达到稳定状态的古冰川，并与古冰川地貌数据对比确定与古冰川地貌特征符合较好的冰川厚度、面积、体积以及ELA等信息［18，54-62］。另外，物质平衡-冰川动力耦合模型也可以采用连续模拟方式模拟冰川的长时间动态变化。如：Kirchner等［63］结合GCM模型与三维SICOPOLIS冰川模型模拟青藏高原末次冰期以来的冰川演变，但模拟的冰川规模与区域地貌所反映的冰川规模差异很大，这可能是由于GCM模型和所使用的冰川模型的分辨率较低，不能合理反映气候和冰川变化的空间分异造成的。王园香［65］利用冰川地貌恢复的ELA结合冻土与孢粉等数据恢复的温度数据模拟了青藏高原末次冰期全盛期（LGM）的冰川规模，但由于气候数据的较低分辨率和不准确性等原因，造成模拟与实测结果相差较大。王园香等［66］使用三维GLIMMER模型对青藏高原的现代冰川变化进行了模拟，模拟结果与实际观测较为接近（误差为8%左右），但在高原东部和内部模拟的冰川面积偏小，而在西北部地区模拟的冰川范围偏大。Yan等［40］利用三维PISM模型对青藏高原冰川进行了模拟，结果表明PISM模型对大型冰帽的模拟效果较好，对山地冰川的模拟结果较差，但总体能够反映高原冰川分布的模式。然而，由于需要长期的连续气候数据和大量的计算资源，利用物质平衡-冰川动力耦合模型对古冰川变化的连续模拟研究还相对较少。

2.2 估算冰川发育时期的古气候参数

地貌-冰面剖面形态模型由于不包括物质平衡和气候驱动，不能直接估算冰川发育时期的古气候参数。但可以结合地貌学方法间接恢复古冰川平衡线（ELA），然后利用经验统计模型恢复冰川发育时期的古气候参数。目前有三种方式可以求解这部分温度变化。

第一种方法假定过去冰川ELA年平均/夏季平均温度（Ta/T6-8；℃）与年累积降水量（Pa；mm）的关系［即P-T模型，式（11），（12）］与现代一致，根据孢粉、湖泊水位以及石笋δ18O等降水代用指标求得降水的变化量，然后将其代入P-T模型，得到由降水的波动导致的温度变化［20，82，117］。并基于ELA的变化量及气温直减率LR求得由于ELA位置的变化导致的气温变化量，两种气温变化量相加则为冰进时的气温波动值。

第二种方法通过更复杂的LR模型求解温度变化。这些模型考虑积累梯度对重建结果的影响，根据ELA处的冰川积累与温度的转换系数f（℃·mm-1）将由ELA变化导致的降水变化转化为相应的温度变化［20，82，116］［式（13）］。

式中：ELAm、Tm、cm分别为现代冰川ELA（m）、在ELAm处的温度（℃）和冰川积累量（mm）。ELAp、Tp、cp分别为古冰川的ELA（m）、在ELAp处温度（℃）和冰川积累量（mm）。

第三种方法根据冰川物质平衡对气候变化的敏感性经验公式求解ELA处的温度和降水变化。例如，Caidong和Sortberg［97］提出念青唐古拉山西部冰川ELA变化与温度和降水变化的经验关系［式（14）］：

这一方法与第一种方法类似，可以根据其他降水代用指标估算降水变化，然后进一步求解温度变化［125］。但是，根据代用指标获取的降水变化会因为代用指标的时空分辨率差异对结果造成误差［126］。如采用石笋δ18O估算的降水信息由于海拔高度的差异并不能够代表冰川区域的降水变化。近年来，一些研究开始通过区域的P-T经验模型和冰川物质平衡对气候要素的敏感性关系［53］或区域多年平均降水和海拔高度的统计关系共同确定冰川ELA处的温度和降水［127-129］。

除上述相对简单的古气候恢复方法外，冰川发育期的古气候参数还可以通过前面1.2.1节介绍的能量物质平衡模型（EMB）或度日模型（DDM）估算ELA变化与温度和降水变化的关系，并由此确定冰川发育时期的古气候参数。EMB模型相对复杂，所需参数较多，需要构建ELA变化与气温、冰川积累量以及影响冰川消融的能量因子（太阳辐射、潜热交换和湍流交换等）变化量之间的关系，具体使用方法参见文献［130-131］。

度日模型（DDM）所需参数较少，在重建冰川发育时期古气候时，首先根据研究区域或其周边地区的气温和降水数据、DDF值及公式（4）确定在现代气候条件下的冰川物质平衡，进而通过对气温与降水组合的不断调整，达到由地貌法估算的古冰川平衡线高度的温度和降水组合。然后再利用其他古气候记录对气温和降水组合的结果进行限定，得到冰川发育时期的古气候特征［93，132］。

利用物质平衡-冰川动力耦合模型对古冰川的稳态模拟可以通过设置不同的温度变化（ΔT：现代气温与历史时期气温的差值；℃）或降水变化（ΔP：现代降水与历史时期降水的比率；%）模拟冰川范围，并与实际观察的冰川末端位置（冰碛垄）对比，得到与冰川发育相对应的温度或降水变化。但由于存在多种ΔT-ΔP组合，研究中可以结合其他气候记录对ΔT-ΔP组合加以限定，以确定古冰川发育时期的古气候特征［18，54-62，132］。

图4总结了青藏高原及其周边山地基于地貌-冰面剖面形态模型（Excel流线模型、GlaRe、Pa⁃leoIce）和物质平衡-冰川动力耦合模型的稳态模拟方式（主要应用二维冰流模型）估算不同冰川发育期次古气候参数的案例研究。由于青藏高原幅员辽阔，这方面的研究还相对较少且分布不均［53，131］，主要集中于高原南部的喜马拉雅山、冈底斯山、念青唐古拉山，东南部的横断山脉，东北部的祁连山、北部的昆仑山垭口和西北部的塔什库尔干等地区，高原中部和北部的研究还很少（图4）。冰川发育的不同期次中，LGM时期的研究最多，其他冰川发育时期的研究尚少。利用物质平衡-冰川动力耦合模型对古冰川的连续模拟可以深入探讨古冰川演化对气候的敏感性和气候驱动机制。如：Yan等［40］利用PISM模型对青藏高原冰川进行了气候敏感性分析，表明高原周边地区的冰川对气候变化的敏感性高于内部的冰川，高原北部的冰川对降水变化较为敏感，而高原东部的冰川对气温变化更加敏感。Yan等［41］将PISM模型与大气环流模型相结合，模拟了青藏高原LGM以来的温度、降水和冰川变化，得出高原的冰川变化主要受夏季温度控制，而区域分异主要受降水变化影响。Yan等［64］还模拟了青藏高原42.5万年来的冰川变化与地球轨道变化的关系，表明高原的冰川变化主要受由岁差引起的太阳辐射变化控制（周期约为2.3万年）。间冰期期间由于温度上升，冰川在高原西部和北部出现大面积退缩，但在高原南部却发生一些冰川扩张，可能与降水增加有关。

图4 青藏高原及其周边山地基于地貌-冰面剖面形态模型（Excel流线模型、GlaRe、PaleoIce）和物质平衡-冰川动力耦合模型的稳态模拟方式（2-D冰流模型）估算的不同冰川发育时期古气候参数的案例研究（基于地貌-冰面剖面形态模型的古气候参数估算方法包括P-T模型、LR模型、ΔT-ΔP在ELA处经验公式、EMB和DDM模型。基于2-D冰流模型的古气候参数主要通过不同的ΔT-ΔP组合确定。MIS-深海氧同位素阶段；LGM-末次冰期全盛期；LD-末次冰消期；LG-晚冰期；EH-早全新世；NEO-新冰期；LIA-小冰期）Fig.4 Summary of the palaeo-climate reconstruction studies for various glacial stages on the Tibetan Plateau and its surrounding mountains based on the landform-ice surface profile models（Excel flowline model，GlaRe，and PaleoIce）and the coupled mass balance-glacial dynamic model（2-D ice flow model）.For the studies using the landform-ice surface profile models，the palaeo-climate information has been estimated based on the P-T model，LR model，theΔT-ΔP empirical relationship at ELA，as well as the EMB and DDM models.MIS-marine oxygen-isotope stages；LGM-Last Glacial Maximum；LD-Last Deglaciation；LG-Lateglacial；EH-Early Holocene；NEO-Neoglacial；LIA-Little Ice Age

2.3 评估年代数据以及由年代数据恢复的古冰川

随着测年技术的发展和完善，很多地区的冰川地貌（尤其是冰碛垄）都得到了年代测定，大大促进了对冰川长期变化特征及其气候-地形驱动机制的认识［17］。然而由于冰川地貌记录的不完整性、受后期地貌过程改造以及测年误差等问题，在一些地区的古冰川发育特征还有很大的不确定性和争论。冰川模型尤其是物质平衡-冰川动力耦合模型可以从另一个角度评估年代数据及其恢复的古冰川特征。例如：Xu等［56］使用二维平面冰流模型重建了贡嘎山海螺沟贡嘎II（Gongga II）冰期时的温度和降水组合，认为该次冰期最有可能发生在LGM时期［134］，而非宇成核素10Be暴露年代方法测定的全新世早期［135］。Yan等［39］使用PISM模型模拟了天山地区末次冰期的变化，认为LGM时期的冰川规模远大于MIS 3时期的冰川规模，与现有年代学数据支持的MIS 3时期在天山地区有更大规模冰进的结果不符。虽然冰川模拟本身也存在输入气候条件等方面的不确定性，冰川模拟研究对进一步细化和完善天山地区的古冰川发育特征具有促进作用。Yang等［19］利用OGGM模型对中国-不丹交界的喜马拉雅山地区的小冰期进行了系统模拟，并与实测小冰期冰碛垄年代和期次进行了对比，发现小冰期的发育年代与实测年代基本符合，但不同规模和地区的冰川可能具有不同的小冰期期次。总体而言，冰川模拟了四次小冰期冰进，但这些冰进在不同的冰川具有不同的表现，有些发育三次小冰期冰进，有些只发育两次，而有些则发育了五次或者更多，冰进次数与冰川对气候变化的敏感性有关，与冰川平均坡度成正比，与冰川长度成反比［19］。由于评估冰川的期次和年代通常需要连续的冰川模拟，而冰川连续模拟在长时期连续气候驱动数据、地形条件以及计算资源等方面还存在很多局限，因此目前这一方面的研究还相对较少。

3 存在问题和未来研究趋势

3.1 冰川模型的进一步改进

目前的冰川模型，即使是三维模型，也大多基于浅冰近似方法（Shallow Ice Approximation），这种方法主要用于受局部地形影响较小的大陆冰盖模拟。山地冰川由于其流动受到谷地地形的约束更大，简单的浅冰近似方法在物理机制上并不完全适用于山地冰川的模拟等，需要基于Navier-Stokes方程的三维冰川模型（如Elmer/Ice模型）。然而由于基于Navier-Stokes方程的三维冰川模型所需的计算资源更大，其在运行效率上还需要改进和提高。近年来，并行计算在计算机领域得到了很大发展，也逐渐运用于冰川模型（如PISM模型），但冰川模型在并行计算方面还需要进一步完善，提高冰川模拟效率。

现有冰川模型大多运行于Linux或Unix操作系统，其输入输出大多是文本、NetCDF或Matlab等文件格式，而输入数据的准备或输出数据的进一步显示和分析一般都需要在GIS软件中进行。同时，如

1.2.3 节所述，冰川模型也可以通过与实测冰川地貌的对比应用GIS叠加分析等方法进行校验。但是，由于目前冰川模型还没有与GIS有机集成，数据准备、结果显示分析和模型校验等还需要与冰川模型分开进行，这样造成冰川模拟、校验和数据分析等的效率不高，同时，由于需要熟悉不同的软硬件环境，也造成冰川模拟的难度较大，对模拟人员的要求也较高。未来应开发能够与GIS有机结合的冰川模型，使冰川模拟的数据准备、参数校验、结果显示和分析等都能够在一个系统中进行，从而大大降低冰川模拟的难度，提高冰川模拟的效率。

现有冰川模型由很多不同的计算机语言开发，包括C、Python、Fortran等，目前很多模型已经实现了开源和共享源代码，使模型在具体冰川模拟中可以进一步的修改和改进，补充和完善更多的模块，如冰川侵蚀模块等。未来研究中应进一步加强冰川模型程序的开源和共享，同时建立一些典型地区的冰川模拟输入数据和模拟结果集，以便不同冰川模型的对比。另外，应该加强冰川模型的培训和学术交流，吸引更多的学者从事冰川模拟的研究。

3.2 古气候数据和物质平衡关系需要进一步研究

冰川模型尤其是连续的冰川模拟需要长时间的连续古气候数据。目前，特定区域的连续古气候数据主要通过树木年轮、冰芯、石笋、湖泊记录等代用指标进行获取。然而，在很多地区这样的数据还很少，需要进一步的研究。一种替代方案是使用GCM模型输出的古气候资料，但GCM模型结果分辨率较粗，Downscaling过程会不可避免地带来其他不确定性。因此，GCM模型的古气候数据在特定区域冰川模拟的适用性还有待进一步评估分析。

现有冰川模型主要根据历史时期观测的冰川物质平衡及其与气候因素的关系驱动古冰川模拟。但当前处于间冰期，冰川总体退缩情况下的物质平衡关系是否能够代表冰进时期的物质平衡关系？另外，古冰川发育时期的冰川总体规模较大，如在北美和欧洲都发育大规模冰盖、在一些地区发育较大规模的冰帽和冰原等，这些大规模的冰川有可能改变地形对气流的遮挡，影响大气环流和降水分布格局，这些变化如何影响冰川的物质平衡还需要更加深入的研究。