突发公共卫生事件应急医疗设施选址研究*
——以邯郸主城区为例
2022-09-15王振报李慧庆祝霜霜
王振报 李慧庆 祝霜霜
0 引言
2020年初新型冠状病毒肺炎(Corona Virus Disease, COVID-19)在全球爆发以来,世界各国经济、社会、民生等方面受到巨大冲击。新型冠状病毒肺炎属突发公共卫生事件下的传染病疫情,具有突发性、不确定性、公共性的特点[1]。突发性是指疫情的爆发突如其来、蔓延迅速;不确定性是指疫情爆发初期,其原因、变化方向、后果难以预测;公共性是指疫情的突发性和不确定性造成公众信息有限性,导致公众心理恐慌、面对疫情无所适从、盲目集中于城市大型医院。因此面对新冠疫情等突发公共卫生事件,城市需要快速调动社会资源,建立应急医疗设施,组织协调社会生活秩序。
近年来,针对城市应急医疗设施的选址主要关注地区人口分布和医生、床位、资金、应急救灾能力等方面的关系[2-4],或是利用地理学区位理论中的空间相互作用模型、泰森多边形等方法确定医疗设施的服务区,再结合医院床位和各个医院服务区内的人口等因素进行选址分析[5-6],其中大部分考虑的是新建医疗设施,对城市现状医疗设施考虑较少。
我国为应对疫情,采取了建设武汉雷神山医院等集中收治新冠疫情患者的应急方舱医院,以及城市封城、社区封闭、人员流动追踪管理等“围堵策略”,虽在防控之下有效控制了人员流动,但由于大型综合医院具备优质医疗资源且往往集中于城市中心[7],部分城市仍出现了居民盲目聚集于大型综合医院的现象(表1),造成院内感染,而城市其他医疗设施却并未得到有效利用,张帆、胡亮等[8-9]研究表明充分利用基层医疗设施,避免盲目集中于综合医院有助于减少人员流动所带来的感染风险。

表1 河北省各级医疗设施病床使用情况Tab.1 the use of hospital beds in medical facilities at all levels in Hebei Province
本文利用GIS网络分析工具,结合城市具体交通路网、医疗设施和居民点分布情况,构建位置分配模型,进行应急医疗设施选址分析,通过将分析求解得到的部分现状医疗设施进行非永久性改造,使之成为针对特定突发公共卫生事件的应急医疗设施,为附近居民点提供相应的救治或隔离等医疗服务。从而充分利用城市现有基层医疗设施,实现对新冠肺炎等突发公共卫生事件无序蔓延的控制。
1 相关概念及模型
1.1 相关概念界定
应急医疗设施是指在突发公共卫生事件发生时,通过城市医护人员和资源的分配、医疗设施的临时改造,形成应急医疗设施,服务于城市各居民点,提供初期医疗服务,如咽拭子采样、医疗用品供应等,并根据患者病危程度进行临时收治和向城市大型综合医院以及新建应急方舱医院转诊。各应急医疗设施组成应对突发公共卫生事件的第一道防线,避免居民盲目聚集于大型综合医院。
1.2 应急医疗设施服务范围及服务能力
《城市居住区规划设计标准(GB50180—2018)》对于新建居住区按照生活圈概念来配置各种公共服务设施,为实现该规划目标,规划区路网需要建立在主干、次干和支路合理的级配结构基础上,才能有利于建立各级生活圈居住区。对于现状老城区或已建成地区,支路网缺乏并且路网密度低[10],导致大部分居民点难以满足5 min或10 min内到达各项配套设施的要求。因此对于已建成地区,选用15 min作为应急医疗设施选址条件更加具有可实施性。利用高德地图开放平台步行路径规划功能,结合Python编程技术和实际对部分居民点的调研,利用GIS对邯郸市主城区基层医疗设施5 min、10 min和15 min步行可达性进行评估(图1),各基层医疗设施服务居民点情况见表2。在当前实际情况下,若按照《城市居住区规划设计标准(GB50180—2018)》要求,有323处居民点(占比约31.73%)未能在步行5 min内到达相应基层医疗设施;而仅有49处居民点(占比约4.81%)未能在步行15 min 内到达相应基层医疗设施。由于本研究应急医疗设施拟从城市已有医疗设施中确定,因此选择15 min步行距离作为应急医疗设施服务范围。
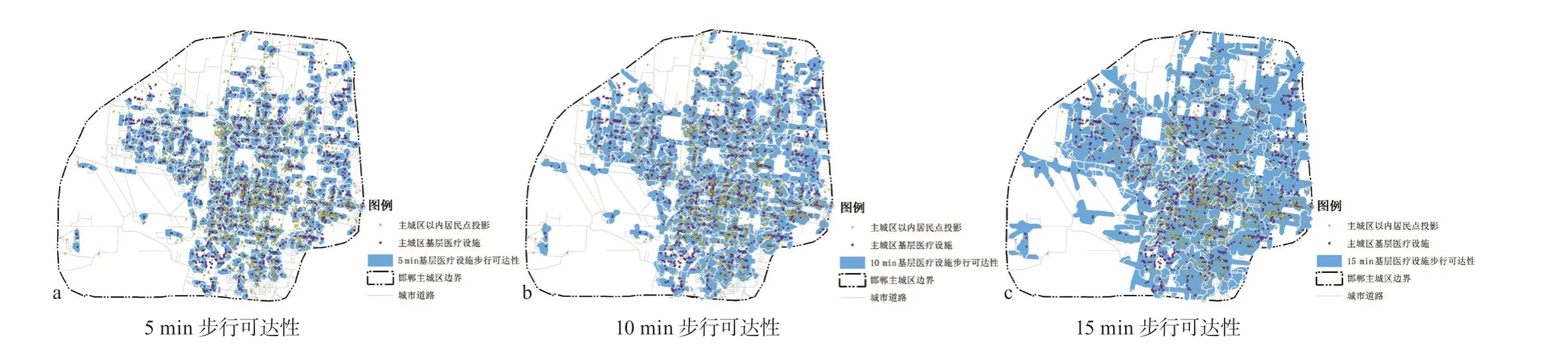
图1 邯郸市主城区基层医疗设施步行可达性Fig.1 walking accessibility of primary medical facilities in the main urban area of Handan City
医疗设施服务能力受床位、医护人员数量、医疗设备、医疗物资储备等多方面影响。但在新冠疫情等突发公共卫生事件下,随着病例的增多,医院床位成为收容、救治感染患者和控制疫情蔓延的关键因素。2021年1月7日,河北省石家庄市召开疫情防控新闻发布会(第三场)。介绍疫情防控情况表明,已将石家庄市第五医院全部腾空,全力收治新冠肺炎患者,同时将河北省胸科医院、石家庄市人民医院、石家庄市三院作为后备腾空医院[11]。2021年1月11日,河北省举行新冠疫情防控发布会(第一场)。卫健委负责人公布河北疫情防控最新动态表明,已腾空河北省胸科医院、邢台市第二医院,分别提供500张和510张床位,专门救治本土病例和无症状的感染者,同时确定2家省级医院和19家市级医院作为后备腾空[12]。在上述保证床位供给的策略下,河北省疫情得到了有效控制,因此本研究以医疗设施床位数作为应急医疗设施服务能力。
1.3 位置分配模型综述
应急医疗设施选址问题属于公共设施的位置分配问题[13],目前应用较为广泛的位置分配模型包括:最小化设施点数模型[14]、最大化覆盖范围模型[15]、最小化阻抗模型[16]、最大化市场份额模型[17]、目标市场份额模型[18]、最大化人流量模型[19]。合理的位置分配可以使私营机构获得更多的客源,减少更多的成本;可以使公共设施获得更高的社会效益[20]。这六类位置分配模型的含义以及适用范围见表3。

表3 六类位置分配模型基本含义及适用情况Tab.3 the meaning and situation of six kinds of facility location models
根据上述六个位置分配模型的基本含义和适用情况,本次研究为突发公共卫生事件下的城市应急医疗设施选址。应急医疗设施属公共服务设施,其选址模型不需要考虑市场份额和同行竞争因素限制,因此选择将最小化设施点数模型、最大化覆盖范围模型作为基础,进行应急医疗设施选址分析。
1.4 最小化设施点数模型
最小化设施点数模型属于罗斯(Roth)[21]在1969年提出的集合覆盖问题(LSCP),1971年图雷加斯(Toregas)等[22]为解决医疗设施选址问题,对集合覆盖问题进行完善并建立了集合覆盖模型,之后不同学者针对具体问题对其进行修正:布罗特科恩(Brotcorn)等[23]提出启发算法和动态规划的方法以解决医疗设施区位重分配问题;特谢拉(Teixeira)等[24]提出等级层次的位置分配模型,以解决不同等级层次的学校选址问题;扎兰迪(Zarandi)等[25]认为大尺度下,人们对公共设施的需求是动态变化的,基于此提出了模拟退火算法,建立了多周期动态选址模型。
考虑到突发公共卫生事件发生时,为控制疫情无序蔓延,而采取的住区“中防控”组团“小隔离”的“围堵策略”[26]。同时要尽可能满足“围堵策略”下居民正常物质文化生活需求所需的公共服务设施配套,结合本文1.2部分确定的应急医疗设施服务范围和服务能力,则最小化设施点数模型可表示为:

式中:
i为居民点编码 (i=1, 2, …, n),
j为医疗设施编码 (j=1, 2, …, m),
xj为所选应急医疗设施j,
z为所选应急医疗设施数目,
Ni为居民点i可达半径之内的服务设施总数。
目标函数(式1)用以保证所选应急医疗设施总数最小;约束条件(式1a)用以保证每一个居民点至少被一个应急医疗设施服务;约束条件(式1b)xj=1表示候选医疗设施j被确定为应急医疗设施,即候选应急医疗设施j可以在15 min步行可达条件下服务至少1个居民点,否则取0。
1.5 最大覆盖范围模型
最大覆盖范围模型问题(MCLP)[27]是为了确定给定数量的设施位置,并使其可以覆盖尽可能多的需求点。此后许多学者根据不同情形对此模型进行了丰富和补充。如霍根(Hogan)和雷维尔(ReVelle)[28]建立了备用设施覆盖模型,以解决在需求点高度集中,可能会导致单个公共设施可靠性不足的情况;彭大江、守爱兵等[29]通过简化算法的手段,提出了最大覆盖选址问题的一种降阶回溯算法,以快速决定应急服务设施是否开设。
在城市无法选定足够多的应急医疗设施点,保证所有居民点在15 min步行可达其所属应急医疗设施的情况下,为最大化应急医疗设施15 min步行可覆盖的居民点数,建立的最大覆盖范围模型为:

式中:
i为居民点编码 (i=1, 2, …, n) ,
j为医疗设施编码 (j=1, 2, …, m) ,
Y为未被应急医疗设施服务到的居民点总数,
yi为若居民点i未被应急医疗设施服务为1,否则为0,
xj为所选应急医疗设施j,
p为所选应急医疗设施数量p,
Ni为居民点i可达半径之内的服务设施总数。
目标函数(式2)用以保证未被应急医疗设施覆盖的居民点最小化,相当于应急医疗设施覆盖居民点的最大化;约束条件(式2a)用以判断居民点是否被至少一个应急医疗设施服务;约束条件(式2b)用以控制应急医疗设施总数为所期望的数量;约束条件(式2c)xj=1表示候选医疗设施j被确定为应急医疗设施,即候选应急医疗设施j可以在15 min步行可达条件下服务至少1个居民点,否则取0;约束条件(式2d)yi=1表示居民点i未被应急医疗设施点服务,即不存在某个应急医疗设施j可以在15 min步行可达条件下服务居民点i,否则取0。
1.6 有容量限制的最大覆盖范围模型
前文所述最小化设施点数模型和最大覆盖范围模型针对的问题是在突发公共卫生事件发生后,根据其所属居民点需求,进行相应医护人员和物资的分配,从而形成应急医疗设施,为城市各居民点提供初期医疗服务。
当需要考虑应急医疗设施服务能力限制时,在最大范围覆盖模型的基础上,通过医疗设施服务能力,与各医疗设施所服务的潜在患病人数,增加选定应急医疗设施的限制条件,构建有容量限制的最大覆盖范围模型,容量限制条件为:

式中:
I为居民点集合,
J为候选应急医疗设施点集合,
i I∈为居民点集合中第i个居民点,
j J∈为候选应急医疗设施中第j个设施点,
di,j为居民点i至应急医疗设施点j的实际距离,
dmax为居民点i的15 min最远步行距离,
P为所选应急医疗设施最大数量P,
Pi为居民点i的突发公共卫生事件潜在感染人口数,
Cj为医疗设施j的服务能力,
Xi,j为居民点i分配至应急医疗设施j时为1,否则为0,
Yj为候选应急医疗设施j被选为应急医疗设施时为1,否则为0。
目标函数(式3)用以保证应急医疗设施覆盖的居民点最大化;约束条件(式3a)用以避免某个居民点被多个应急医疗设施服务;约束条件(式3b)用以控制所选应急医疗设施总数不超过医疗设施最大数量;约束条件(式3c)用以保证各应急医疗设施所服务的就诊居民数量不超过其服务能力;约束条件(式3d)用以保证居民点i至某个应急医疗设施j可以在15 min步行可达条件下;判断条件(式3e)用以判断居民点i是否被某个应急医疗设施j服务;判断条件(式3f)用以j是否被确定为应急医疗设施。
2 应急医疗设施选址求解
2.1 研究范围概况
以邯郸市主城区为研究范围,总用地面积为90.12 km²,包含邯山区、丛台区、复兴区三个行政区域,居民点1018处,基层医疗服务设施共1504处,综合医院64处。通过邯郸市主城区居民点及医疗设施分布概况(图2),可以看出居民点和医疗设施分布大致呈中间密、四周疏的格局;床位等医疗资源集中于城市中心的大型综合医院,基层医疗设施建设薄弱。

图2 邯郸市主城区居民点及医疗设施分布概况Fig.2 distribution of residential areas and medical facilities in the main urban area of Handan City
2.2 数据获取及构建交通网络模型
邯郸市行政区划数据来源于邯郸市行政地图,城市路网数据来源于OSM(open street map, OSM)开源地图,并结合实际对路网进行修改和补充。城市医疗服务设施点及居民点来源于百度地图POI(point of interest, POI)采集,所采集到的POI包括类别、经纬度、名称等基本信息。各居民点户数信息来源于安居客网站小区信息板块;各医疗设施等级和床位数来源于邯郸市各医院官方网站。
将邯郸市道路数据导入GIS的文件地理信息库,并通过人工检查修复错误的道路拓扑关系,导入邯郸市主城区医疗设施POI和居民点POI,从而完成GIS交通网络模型(图3)的构建。
图3 邯郸市主城区交通网络模型Fig.3 traffic network model of the main urban area of Handan City
2.3 位置分配模型
2.3.1 必选应急医疗设施及其可达性
三甲综合医院集中了一个城市最大规模和最优技术力量,具备应对突发公共卫生事件能力。因此,邯郸市主城区的三甲综合医院将设定为应对突发公共卫生事件的必选应急医疗设施点。
选取人的步行速度为1.25 m/s[30],以各个居民点到各个应急医疗设施的实际路程为距离,求解出较为科学合理的必选应急医疗设施15 min步行可达性(图4)。可以看出四所必选应急医疗设施仅能覆盖237个居民点,占比23.28 %,因此在应对突发公共卫生事件时,需要增加应急医疗设施点,以保证在15 min步行时间以内服务到尽可能多的居民点。
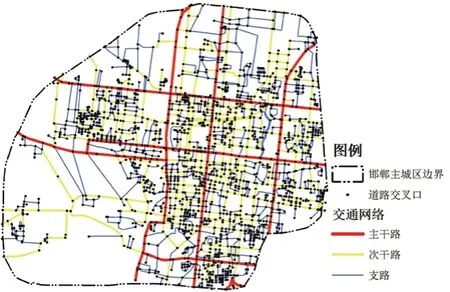
图4 必选应急医疗设施15 min可达性Fig.415 min accessibility of required emergency medical facilities
2.3.2 最小化设施点数模型求解
利用最小化设施点数模型及邯郸市主城区交通网络,GIS网络分析工具求解应急医疗设施位置,保证所选应急医疗设施可在步行15 min内覆盖邯郸市主城区各居民点,通过最小化设施点数模型应急医疗设施求解结果(图5a),所求解应急医疗设施覆盖居民点占比(图5b),在四所必选应急医疗设施的基础上,需要将图中所示51所现状医疗设施进行非永久性改造,使其成为应急医疗设施,应对特定的突发公共卫生事件,虽可覆盖邯郸市主城区各居民点,但是可以看出部分应急医疗设施点利用率较低。
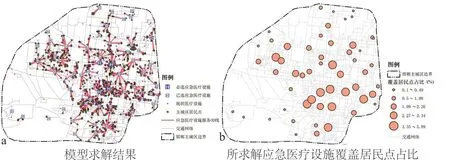
图5 最小化设施点数模型应急医疗设施求解Fig.5 minimizing facility points model for solving emergency medical facility
2.3.3 最大覆盖范围修正模型求解
在应对突发公共卫生事件时,若受到资源条件限制,则可利用最大覆盖范围修正模型求解,所求解得到的应急设施点数可以实现在有限制的条件下,实现应急医疗设施点的最大效益。通过试验,得到在不同数目的应急医疗设施点情况下应急医疗设施覆盖居民点数(图6),可以看出选定20~24所应急医疗设施,可以保证较高的覆盖居民点数,但是当要确定的应急医疗设施点数量大于24个时,应急医疗设施覆盖居民点数增加幅度明显减小。
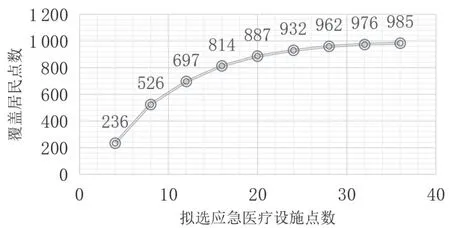
图6 最大覆盖范围模型应急医疗设施覆盖居民点数试验分析Fig.6 the test analysis results of maximizing the coverage of emergency medical facilities coverage for resident points
选取期望确定24个应急医疗设施,进行GIS网络分析工具位置分配中最大覆盖范围模型求解,并限定居民点到应急医疗设施15 min步行可达,得到最大覆盖范围模型应急医疗设施求解结果(图7a),所求解应急医疗设施覆盖居民点占比(图7b)。将图中所示21所现状医疗设施进行改造,使其成为应对特定突发公共卫生事件的应急医疗设施点,可覆盖约93%的居民点,且各应急医疗设施相比于最小化设施点数模型具备较高的覆盖居民点占比。

图7 最大覆盖范围模型应急医疗设施求解Fig.7 solution of the modified model of maximizing coverage problem
2.3.4 有容量限制的最大覆盖范围模型求解
胡永峰、刘立平等学者关于新型冠状病毒感染与发病流行病学特征进行分析,得出新型冠状病毒密切接触者总感染率为6.23%(237/3807)[31]。本文假设该感染率乘以邯郸市主城区各居民点人口数,得到潜在感染人群分布(图8a)。由邯郸市主城区各医疗设施床位数以及有容量限制的最大覆盖范围模型,得到在不进行医护人员和医疗物资的应急分配,同时通过病房临时改造和建设医疗方舱等手段快速扩容的条件下,选定应急医疗设施(图8b),并分析求得选定的应急医疗设施服务居民点数(图8c),服务潜在感染居民点人口数(图8d)。

图8 有容量限制的最大覆盖范围模型应急医疗设施求解Fig.8 the maximum coverage model with capacity constraints for emergency medical facilities solution
3 结果与讨论
为实现对城市现有基层医疗设施的充分利用和对新冠肺炎等突发公共卫生事件无序蔓延的控制,从而保证居民在控制疫情“围堵策略”下正常的生活秩序,本文利用GIS网络分析工具位置分配模型,结合邯郸市主城区医疗设施和居民点数据,进行应急医疗设施选址和分配。利用最小化设施点数模型和最大覆盖范围模型,得出根据各居民点所需,对选定应急医疗设施不同服务能力进行相应的资源调度,使居民点居民能够及时得到必要的医疗服务;利用有容量限制的最大覆盖范围模型,得到各医疗设施在现有服务能力条件下,结合以新型冠状病毒密切接触者感染率确定的潜在感染人群,进行应急医疗设施选址和分配。各应急医疗设施选址结果对比见表4。可以看出:

表4 四种情况下应急医疗设施选址结果对比Tab.4 comparison of facilities locations of emergency medical facilities in four cases
第一,当发生突发公共卫生事件时,若城市资源不充足,仅能把四所规模设施和技术力量均为最优的三甲综合医院作为应急医疗设施,在这种情况下:四所应急医疗设施在15 min步行可达性的要求下平均服务居民点数为61,单所应急医疗设施利用率最高,但可以覆盖到的居民点占比仅为23.28 %。
第二,若资源充足,希望可以在15 min步行可达性的条件下,通过医护人员和资源调度,使所选应急医疗设施具备服务城市全部居民点的能力,则采用最小化设施点模型求解,在这种情况下:需要将36所现有医疗设施确定为应急医疗设施以实现服务全部居民点,但是平均服务居民点数仅为24,部分应急医疗设施利用率低。
第三,当资源较为充足时,虽无法在15 min步行可达性条件下覆盖全部居民点,但可以利用最大覆盖范围模型进行分析求解,使得各个应急医疗设施具备较高的利用率,在这种情况下需要将21所现有医疗设施确定为应急医疗设施,所能服务的居民点占比为93.22%,平均服务居民点数为37,相比于最小化设施点模型具备较高的覆盖居民点占比。
第四,在考虑现状医疗设施服务水平和能力时,根据各医疗设施现有床位数和以新型冠状病毒密切接触者感染率确定的潜在感染人群,不考虑医护人员和物资的重新调度和再分配,利用有容量限制的最大覆盖范围模型进行应急医疗设施求解,可服务392处居民点,各应急医疗设施有效服务居民点均值为6处,所能服务的居民点占比为38.50%。因此建议在考虑容量限制的最大覆盖范围模型基础上,结合最小化设施点数模型进行应急医疗设施选址分析,通过医护人员和医疗物资的分配提高应急医疗设施服务居民点占比。
虽然最小化设施点模型求解结果中部分设施点服务居民点比例较低,但在突发公共卫生事件发生时,通过医护人员和物资的调度和再分配,根据不同片区的需求,可以有针对性地建立应急医疗设施。此外,在未来可结合公共安全与医疗卫生方面原理,针对不同类型的城市突发公共卫生事件建立特定的应急设施候选库。当遇到某一突发公共卫生事件时,可以迅速调用特定的应急设施候选库,利用本研究提出分析方法与模型进行快速选址分析。建立应急医疗设施体系,从而实现对城市医疗设施的充分利用,构成城市应对突发公共卫生事件的第一道防线,避免患者“用脚投票”,盲目集中于城市大型综合医院。
此外,本文的案例选取床位数作为应急医疗设施的服务能力,在实际应用中需要酌情考虑,原因是一些医疗设施在短时间内可能难以腾空全部床位,在以后的研究中可以按照一定比例的床位数(例如50%或70%)作为应急医疗设施的服务能力,按照位置分配模型进行应急医疗设施选址。
图表来源:
图1-8:作者绘制
表1:根据河北省卫生健康委员会统计信息中心、河北省医学情报研究所数据绘制
表2-4:作者绘制
