Inter‑satellite Link Topology Design and Relative Navigation for Satellite Clusters

，

College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，P.R.China

Abstract: A distributed relative navigation approach via inter-satellite sensing and communication for satellite clusters is proposed.The inter-satellite link（ISL）is used for ranging and exchanging data for the relative navigation，which can improve the autonomy of the satellite cluster.The ISL topology design problem is formulated as a multi-objective optimization problem where the energy consumption and the navigation performance are considered.Further，the relative navigation is performed in a distributed fashion，where each satellite in the cluster makes observations and communicates with its neighbors via the ISL locally such that the transmission consumption and the computational complexity for the navigation are reduced.The ISL topology optimization problem is solved via the NSGA‑Ⅱalgorithm，and the consensus Kalman filter is used for the distributed relative navigation.The proposed approach is flexible to varying tasks，with satellites joining or leaving the cluster anytime，and is robust to the failure of an individual satellite.Numerical simulations are presented to verify the feasibility of the proposed approach.

Key words：satellite cluster；relative navigation；inter-satellite link；network topology；multi-objective optimization

0 Introduction

Satellite clusters which consist of multiple co‑operative satellites have received increasing atten‑tions in recent years.Multi-satellite system has sev‑eral advantages over the traditional monolithic satel‑lite，such as lower price，increased flexibility and ro‑bustness to the failure of an individual satellite，and hence，it has great potential in distributed aperture telescopes，deep space exploration and other space missions［1-2］.

For the satellite cluster in deep space，naviga‑tion is a challenging problem［3］.There are a signifi‑cant number of satellites in the cluster，so the com‑putational cost for navigation is expensive.Further，in many tasks，the satellites in the cluster are not re‑quired to track specified relative motion in contrast to the formation，so the relative states between sat‑ellites vary frequently，which poses extra challenge for real-time navigation with high accuracy.More‑over，for deep space missions，there are scenarios when the global navigation satellite system（GNSS）is not available or the satellites cannot contact with the ground frequently［4-5］.Therefore，to improve the autonomy of the multi-satellite system，a lot of work has been carried out on the relative navigation via inter-satellite links with limited on-board mea‑surements［6］.

An inter-satellite link（ISL）is a link used for communication between satellites and has a function of sensing［7］.Both radio-frequency（RF）links［8］and laser links［9］can be used for the relative naviga‑tion.The laser links can achieve high ranging accura‑cy while require higher power consumption.Thus，for small satellites with limited resources，relative navigation using RF links with high frequency is playing an important role at present.

The inter-satellite relative range or angle mea‑surements are taken when the links are established，and the data are transmitted between neighbors via ISLs，thus designing the ISL network topology be‑comes important for both communication and navi‑gation［10］.For example，the energy consumption for transmitting or receiving data is related to the dis‑tance between satellites，which is changing in time，and hence，there has considerable work been done on optimizing the ISL topology to reduce the total energy consumption［11-12］.Moreover，massive data packets are transmitted between satellites，which may cause the network congestion，and affect the navigation performance.Therefore，ISL assignment approaches such as reinforcement learning based al‑gorithm［13］have been proposed.Other research fo‑cuses on improving the navigation performance，and the position dilution of precision（PDOP）criterion is proposed for the ISL assignment problem［14-15］.

Another important issue needs to be addressed for the relative navigation arises from the fact that the number of the satellites in the cluster is huge.Traditional centralized state estimation algorithms，such as extended Kalman filter（EKF）［16］，require to transmit all the measurements to a center satel‑lite.While the performance of the centralized algo‑rithm is optimal，it might be infeasible since the transmission consumption and the computational cost are huge.Therefore，distributed state estima‑tion algorithms have attracted a lot of attentions，and have been widely used in multi-agent systems［17］and sensor networks［18］.The main idea of the distributed algorithm is that for each agent in the network，the information is only exchanged between neighbors，and each agent makes a local estimation using the data.Distributed estimation with applications in spacecraft navigation has been studied recently［19-20］.For example，a distributed information fusion algo‑rithm is proposed to estimate the orbit of a single spacecraft using information from ground stations in the network［21］.For the relative navigation of multi‑ple spacecrafts，a consensus extended Kalman filter algorithm is proposed with the observability analy‑sis［22］.Different consensus-based state estimation al‑gorithms，including consensus on information（CI），consensus on measurement（CM）and hybrid methods have been presented with stability analy‑sis［23］.Since the optimality of the CI algorithm can be guaranteed with appropriate assumptions，thus，in this paper we design a RF-based ISL topology to meet the assumptions made in CI algorithm，and propose a distributed relative navigation scheme for clusters，where satellites only exchange navigation informations and take inter-satellite measurements with satellites in neighbours via ISLs.

The main contributions of this paper are sum‑marized as follows：

（1）A time-varying sensing and communica‑tion ISL topology network is designed，and it can adapt to complicated tasks，with satellites joining or leaving the network at any time.

（2）Both the energy consumption and the navi‑gation accuracy are taken into account when design‑ing the ISL topology，which makes it more feasible in practice.

（3）A consensus-based Kalman filter algorithm is used for estimating the states of the satellite clus‑ter in a distributed fashion，and the computational load as well as the transmission consumption is re‑duced with guaranteed stability.

The rest of the paper is organized as follows.In Section 1，the system model including the relative motion model and the observation model is intro‑duced.In Section 2，the ISL topology optimization problem is formulated and in Section 3，the distrib‑uted relative navigation algorithm is presented.In Section 4，numerical results for a cluster with 15 satellites are presented.Finally，Section 5 con‑cludes the paper.

1 System Model

In this section，we briefly introduce the relative navigation scheme for satellite clusters，including the relative orbital dynamics and the observation model.

1.1 Relative orbital dynamics

For the satellite clusters system，the local-ver‑tical-local-horizontial（LVLH）coordinate frame originates from the barycenter of the chief satellite is used，wherex-axis lying along the orbital radius vectorrcfrom the Earth center to the chief satellite，z-axis coinciding with the satellite angular moment vector，andy-axis coinciding with the satellite veloc‑ity vector，shown as Fig.1.

Fig.1 Satellite orbital coordinate system

Assuming that the orbit of chief satellite is cir‑cular and the relative distance between two satellites is not large，the relative orbital motion for any depu‑ty satellite can be described by the Clohessy-Wilt‑shire equation as

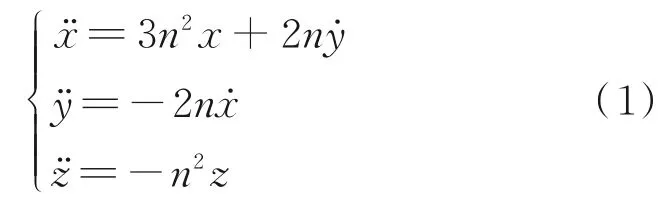
wherenis the orbit angular velocity of the circular reference orbit andr=[x，y，z] the triaxial compo‑nents of the deputy satellite’s relative positions in the LVLH frame.

Nas the state for theith satellite，then the discretetime state space model is given by

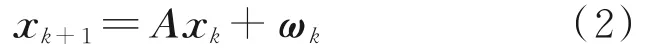
whereA=diag(A1，A2，…，AN) withAias the state transition matrix for theith satellite，diag(⋅)represents the diagonal matrix with(⋅) as the diago‑nal entries，and

Denotexk=x（kΔt）［x1（kΔt）T，…，xN（kΔt）T］T∈as the system state at timekΔt，with Δtas the sampling time andnx=6Nas the dimension of the system state of the cluster；ωk～N(0，Qk)is the pro‑cess noise and is assumed to be Gaussian white noise with zero mean and covarianceQk.

1.2 Multi‑satellite relative navigation scheme

In this paper，the sensing and communication are conducted via inter-satellite RF links.Relative navigation based on angles-only，range-only and mixed measurements has been studied well.Al‑though angles-only relative navigation［24-25］and range-only relative navigation［26］require fewer mea‑surement devices to complete the relative orbit de‑termination，the observability problem still exists.Therefore，in order to improve the navigation accu‑racy and reduce the total number of measurements，the multi-satellite navigation scheme is adopted［8］.

Suppose all satellites in the cluster can measure the range and angle information and be divided into two groups，At each time step，both inter-satellite angle and range measure‑ments are taken between satelliteswhile only range measurements can be taken between oth‑er satellites.The multi-satellite relative navigation scheme with {C1，C2，C3} and {D1，D2，…，D6} is shown in Fig.2.

Fig.2 Multi-satellite relative navigation example

For each satellitei，the observation model is given as

2 Inter‑satellite Link Topology Op‑timization Problem Formulation

In this section，we design a time-varying ISL topology for clusters with a large number of satel‑lites.The energy consumption as well as the naviga‑tion performance is considered，with the ability to switch the satellites taking both range and angle measurements in an event-triggered fashion to ex‑tend the average working time of the whole cluster.The ISL topology optimization problem is formulat‑ed as a multi-constraint multi-objective problem and is described in detail below.

2.1 Network topology

Satellite clusters perform inter-satellite sensing and communication through a time-varying network topology G=(V，E，A)，whereV=[v1，v2，…，vN]represents the satellite nodes in the network，and E represents the connections between the satellite nodes，with (vi，vj)∈E indicating that the ISL is es‑tablished between satelliteiandj.Denote the neigh‑bors ofvias Ni≜{vj∈V，|(vi，vj)∈E}，and hence，Niincludes satellites that establish ISL withvi.Moreover，the adjacency matrix A(G)is defined as

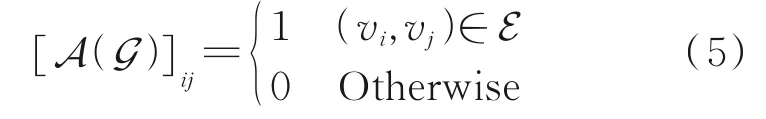
and the Laplacian matrix L(G)is defined as

Notice that the topologyG(k) changes in time，and we design the optimal topology as follows.

2.2 Constraint formulation

In this paper，the following constraints are con‑sidered.

（1）Number of ISL

Since each satellite can carry limited number of RF equipments，limited number of ISLs can be es‑tablished.We suppose for each satellite，at least one link and at mostlmaxlinks are established.

（2）Connectivity of the topology

The communication topology is connected if there exists a path connecting any two satellites.The connectivity of the topology could be satisfied when the second smallest eigenvalue of the Lapla‑cian matrix L(G)is positive，i.e.

whereμ2(⋅) denotes the second smallest eigenvalue of(⋅).

（3）Symmetry of ISL assignment matrix

In this paper，we assume that when the ISL be‑tween two satellite is established，sensing and com‑munication between two satellites are possible in both directions，and hence，the network topology is an undirected graph.

The ISL assignment matrix can be described as a two-dimensional symmetric matrix，shown as

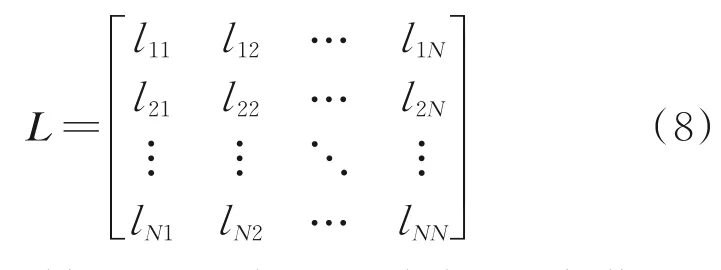
wherelijis a binary number，andlij=1 indicates that there exists a link between satelliteiandj，wheni≠j.liiindicates that the satelliteican estab‑lish a link with the chief satellite.We require thatLis symmetry，i.e.

Remark 1Constraint（1）is proposed to meet the requirements in real applications.Constraints（2）and（3）are proposed such that the ISL topol‑ogy is an undirected and connective graph.

2.3 Performance metrics

2.3.1 Navigation accuracy

PDOP can reflect both the number of inter-sat‑ellite observations and the geometric distribution of inter-satellite observations，and hence，PDOP crite‑rion is taken as a measure of navigation accuracy per‑formance，which is calculated as

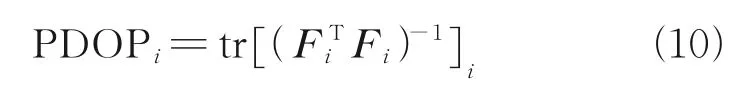
whereFiis an observation matrix for satelliteiwithsISL links，shown as

whereRijis the range between satelliteiand satel‑litej，() the position of satellitei，and(xj，yj，zj) the position of satellitej，forj=1，2，…，s.

2.3.2 Energy consumption

Suppose the distance between transmitting and receiving modules isd，then the energy consump‑tion of the transmitting modules when transmittingabit of data is expressed as

The energy consumption of the satellite when receivingabit of data is

Therefore，the energy consumption in a satel‑lite cluster network is given as

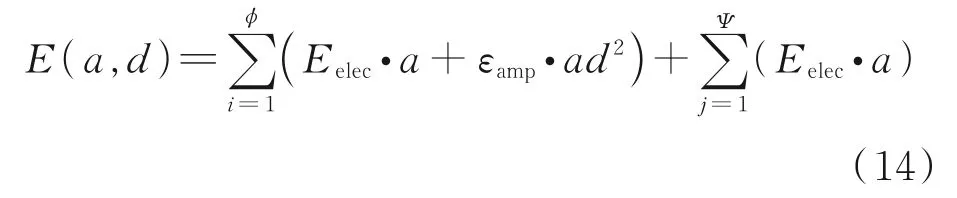
whereEelecdenotes the energy consumption of the transmitter and receiver modules when transmitting or receiving 1 bit of data，Eampis the energy con‑sumption per square meter，andΦandΨare the to‑tal numbers of links for the satellite to send and re‑ceive data，respectively.

2.4 Optimization problem

We consider scenarios when the inter-satellite distance is changing，and satellites can join or leave the cluster anytime during missions.The dynamical‑ly varying ISL topology optimization problem is for‑mulated as：At each time step，finding the optimal adjacency matrixL，such that

with constraints

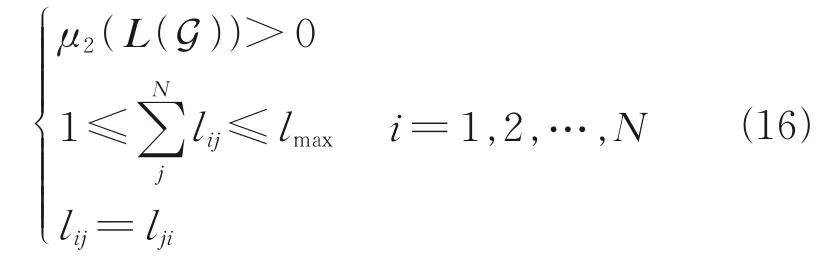
Further，to avoid excessive energy consump‑tion for satellites taking both range and angle mea‑surements，we set a thresholdUfor the total energy consumption.And once the total energy consump‑tion exceeds the threshold，the satellite taking both range and angle measurements is switched to the sat‑ellite with the smallest energy consumption in the cluster.

3 Relative Navigation Algorithm Based on Inter‑satellite Link To‑pology Optimization

In this section，we propose a relative naviga‑tion algorithm for the satellite cluster，which solves the inter-satellite link topology optimization problem at each time step via NSGA-Ⅱalgorithm for the op‑timal sensing and communication topology，and then performs a distributed state estimation for rela‑tive navigation via the consensus Kalman filter algo‑rithm.

3.1 NSGA‑Ⅱalgorithm

The multi-objective optimization problem can be solved via many approaches，and in this paper，a modified genetic algorithm，NSGA-Ⅱalgorithm，is used［27］.The flowchart of NSGA-Ⅱ algorithm is shown in Fig.3，where gen is the nmber of generation.

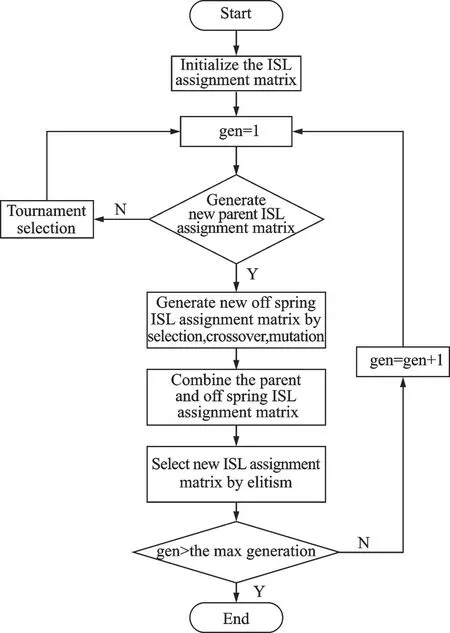
Fig.3 Flowchart of NSGA-Ⅱalgorithm

When initializing the ISL assignment matrix，all the constraints in Section 2 need to be satisfied.After establishing the initial population，selection，crossover，mutation，and elite retention are per‑formed iteratively for solving the optimal link assign‑ment matrix.

3.2 CI Kalman filter algorithm

For cluster with a large number of satellites，in‑formation filter is more computationally efficient than the traditional Kalman filter when the size of the measurement vector is large.Therefore，in this paper，a distributed consensus Kalman in informa‑tion form is used.At each time step，satelliteviper‑forms information filter locally with its own mea‑surements，communicates with neighbors，and then performs the consensus step forMiterations.The CI Kalman filter algorithm is shown in Algorithm 1.

Algorithm 1CI Kalman filter algorithm

Remark 2Since the system is stable，and the undirected graph is connected，it has been shown that the estimation error using CI filter designed in this paper is bounded for any number of consensus it‑erationsM［23］.

4 Numerical Simulation

In this section，a satellite cluster with 15 satel‑lites is used to verify the proposed relative naviga‑tion approach.

The orbit elements are set as follows.The semi-major axis of all satellites is 7 100 km.The ec‑centrincity，inclination，right ascension of the as‑cending node，argument of perigee and mean anom‑aly of the chief satellite are 0，30°，120°，60°and 45°，respectively.The eccentrincity of the 14 deputy sat‑ellites is 0.000 3，and the inclination，right ascen‑sion of the ascending node，argument of perigee and mean anomaly of 14 deputy satellites are randomly chosen between 29.9°—30.1°，119.9°—120.1°，59.9°—60.1°，and 44.9°—45.1°，respectively.

There are three satellites taking range and an‑gle measurements，and the other satellites only take range measurements.The simulation is run for［0，12 000］s，with the sampling time Δt=60 s.Each satellite can establish at most three links.The pa‑rameters in energy consumption metrics are chosen asEelec=100 nJ/b，εamp=50 pJ/(b ⋅m2).a=6 b when data is transmitted or received by inter-satel‑lite communication，a=3 b when taking inter-satel‑lite range and angle measurement，anda=1 b when taking inter-satellite range measurements only.

The NSGA-Ⅱalgorithm is used for ISL topol‑ogy optimization，with 50 iterations，chromosome crossover rate 0.9 and gene mutation rate 0.1.Me‑tropolis weights［28］are used for the consensus step.

In the following，two different simulation sce‑narios are considered.

4.1 Relative navigation with dynamically vary‑ing ISL topology

Fig.4 shows the Pareto frontier of NSGA-Ⅱal‑gorithm.The non-dominated solutions（marked by the red stars）obtained by NSGA-Ⅱalgorithm con‑verge after 50 generations approximately.

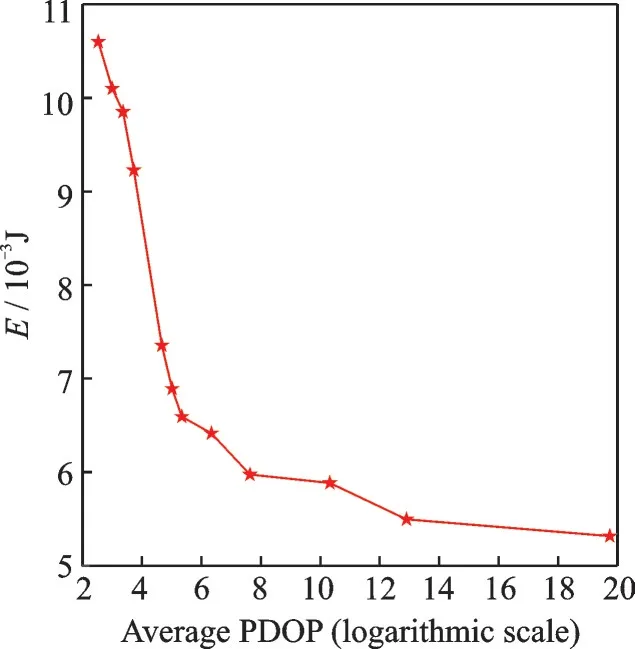
Fig.4 Pareto frontier of NSGA-Ⅱalgorithm

Fig.5 shows the ISL topologies at two consecu‑tive sampling moments.The total energy consump‑tion of Satellite 14 exceeds the threshold at 2 400 s，and is replaced by Satellite 1.From Fig.5（a）and Fig.5（b），it can be seen that the ISL topology is re‑designed with Satellite 1 taking range and angle measurements.

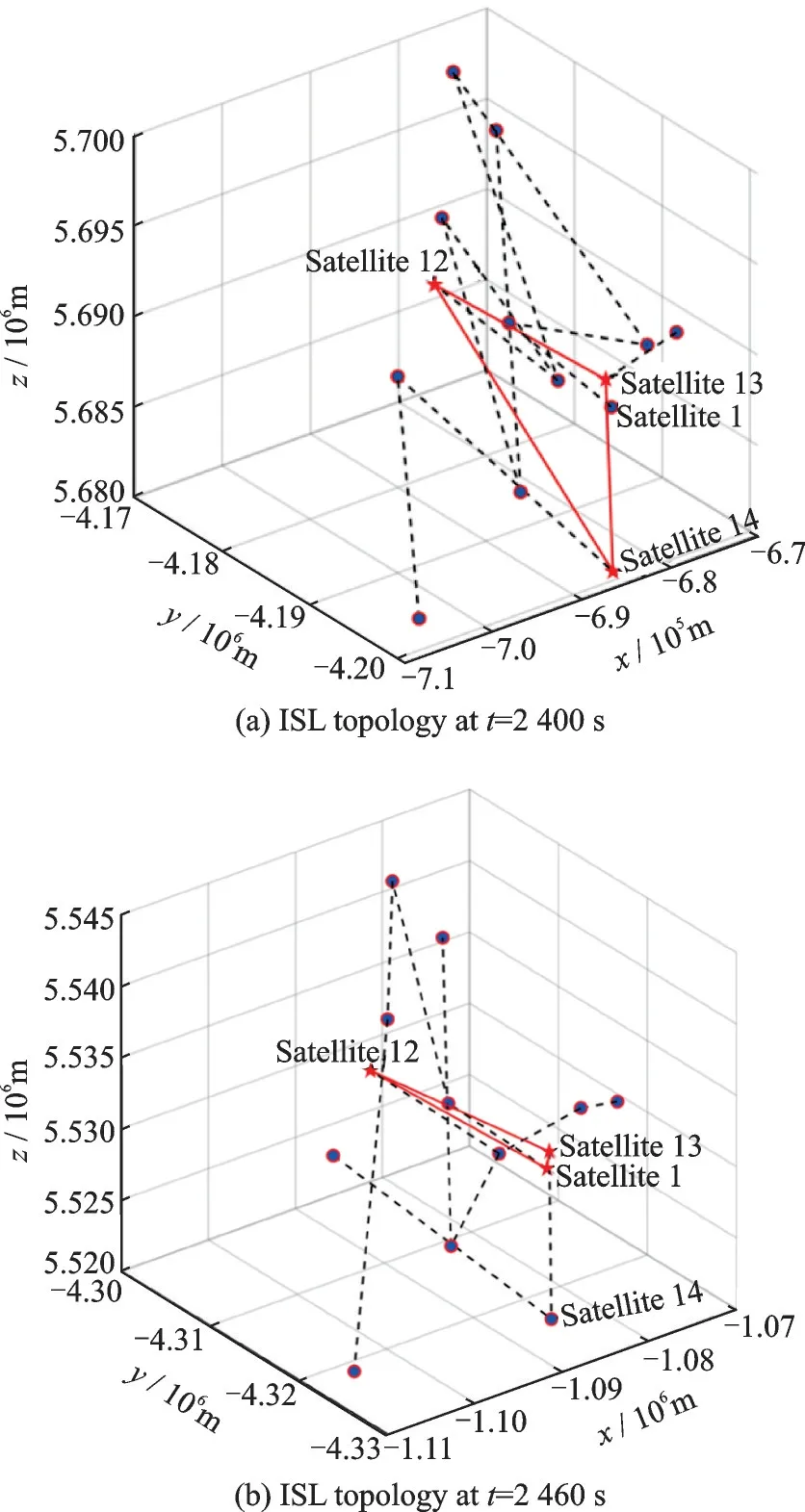
Fig.5 ISL topologies with satellite taking range and angle measurements replaced

Fig.6 shows the energy reduction with the pro‑posed approach.In Fig.6（a），we compare the total energy consumption of the entire satellite cluster us‑ing the optimal ISL topology with the one using a fixed topology.The fixed topology is chosen to be the optimal topology designed at the first sampling time.It can be seen that the total energy consump‑tion is reduced about 22.2% at the end of the simula‑tion.In Fig.6（b），we show the energy consumption of Satellite 14.Satellite 14 is used for taking the range and angle measurements beforet=2 400 s，and after that，it is replaced by Satellite 1.It can be seen that the energy consumption of Satellite 14 is significantly reduced compared with the case if it is not replaced.Thus，it can be verified that the dy‑namically adjustments of ISLs can extend both the average working time of an individual satellite and the entire cluster.

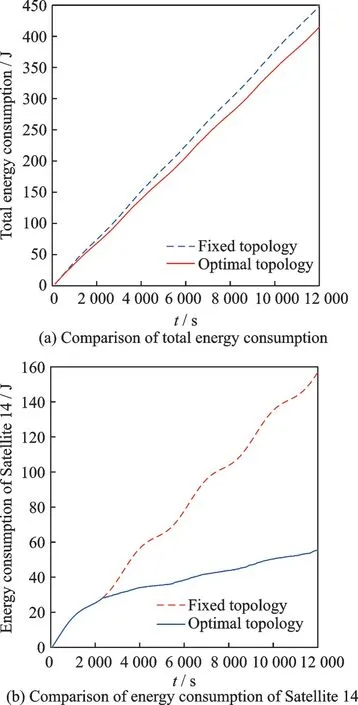
Fig.6 Comparison of energy consumption

Fig.7 shows the state estimation errors for one satellite using the proposed distributed algorithm.The centralized EKF algorithm is used as a bench‑mark.The errors and 3σbounds using both algo‑rithms are shown.It can be seen that albeit the error covariance of the consensus Kalman filter is larger than the centralized one initially，the error covari‑ance converges，and the estimation errors and the converged error covariance of the consensus Kalman filter are quite close to the centralized one.

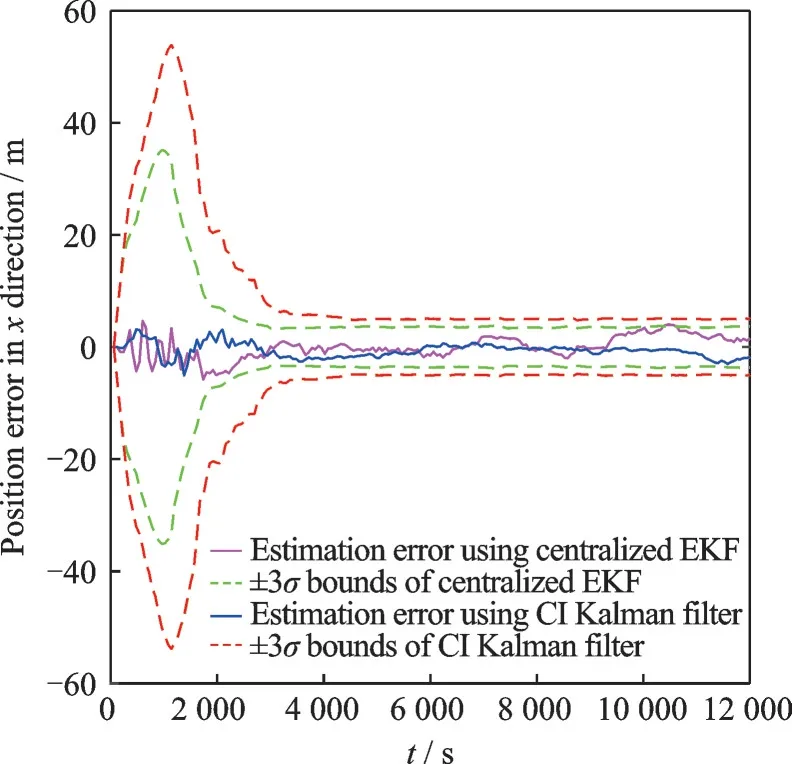
Fig.7 Comparison of navigation performance

4.2 Relative navigation with satellite leaving cluster randomly

Next，we consider the situation when a satel‑lite leaves the cluster randomly.Fig.8 shows the ISL topology at two consecutive sampling mo‑ments，before and after Satellite 11 leaves the clus‑ter.From Fig.8（a），it can be seen that if Satellite 11 leaves the cluster，Satellite 9 would be discon‑nected from the entire network，therefore Satellite 9 has to be reconnected to the cluster or the state esti‑mation of Satellite 9 would become inaccurate.In Fig.8（b），it can be seen that Satellite 9 is reconnect‑ed to the cluster with new ISL topology designed at the next sampling time.

Fig.8 ISL topologies before and after Satellite 11 leaving cluster

Fig.9 shows the local estimation from Satellite 1.It can be seen that with the connective ISL topol‑ogy，the state of Satellite 9 could be estimated accu‑rately by any other satellites.

Fig.9 Estimation error for Satellite 9

Therefore，it can be seen that the proposed rela‑tive navigation scheme can optimize the ISL topolo‑gies in different scenarios，and the total energy con‑sumption of the cluster is reduced.Further，the pro‑posed distributed consensus Kalman filter algorithm can be used for the relative navigation effectively.

5 Conclusions

We consider the relative navigation problem for satellite clusters using inter-satellite sensing and communication.The time-varying ISL topology is optimized to reduce the energy consumption and im‑prove the navigation performance.Then a CI Kal‑man filter is used for the state estimation in a distrib‑uted fashion.The proposed approach is flexible and robust to different tasks.Simulation results show the effectiveness of the proposed approach.

Future work includes：（1）extending the timetriggered communication and navigation scheme to the event-triggered scheme for further reducing the communication consumption and（2）taking into ac‑count the transmission delay in designing the ISL to‑pology as well as the distributed filtering algorithm.