Attitude Control of a Flexible Solar Power Satellite Using Self‑tuning Iterative Learning Control

GAO Yuan，WU Shunan，LI Qingjun

School of Aeronautics and Astronautics，Sun Yat‑sen University，Shenzhen 518107，P.R.China

Abstract: This paper proposes a self-tuning iterative learning control method for the attitude control of a flexible solar power satellite，which is simplified as an Euler-Bernoulli beam moving in space.An orbit-attitude-structure coupled dynamic model is established using absolute nodal coordinate formulation，and the attitude control is performed using two control moment gyros.In order to improve control accuracy of the classic proportional-derivative control method，a switched iterative learning control method is presented using the control moments of the previous periods as feedforward control moments.Although the iterative learning control is a model-free method，the parameters of the controller must be selected manually.This would be undesirable for complicated systems with multiple control parameters.Thus，a self-tuning method is proposed using fuzzy logic.The control frequency of the controller is adjusted according to the averaged control error in one control period.Simulation results show that the proposed controller increases the control accuracy greatly and reduces the influence of measurement noise.Moreover，the control frequency is automatically adjusted to a suitable value.

Key words：iterative learning control；attitude control；solar power satellite；fuzzy control

0 Introduction

Constructing solar power satellites in space and transmitting the energy to the ground is a potential way to generate clean and renewable energy and re‑alize carbon neutrality in the future［1-2］.One difficul‑ty of the solar power satellite is the precise attitude control of the ultra-large space structures because the attitude control accuracy would be influenced greatly by the ultra-flexibility of the structure or measurement noise［3］.

Various researchers have studied the attitude control challenges of the ultra-large space struc‑tures，such as flexible solar sails［4-5］and flexible space manipulators［6］.However，the studies on atti‑tude control of solar power satellites are not suffi‑cient.Wie and Roithmayr proposed an orbit-attitude coupled control scheme for a solar power satellite us‑ing electric thrusters［7］.They found that the gravity gradient torque is the main attitude disturbance for ultra-large solar power satellite due to large moment of inertia.Wu et al.［8］proposed a robust optimal con‑trol algorithm with a disturbance rejection technique using internal model principle.However，Refs.［7-8］mainly concentrated on attitude control of a sin‑gle rigid body.Zhang et al.［9］considered the flexibili‑ty of the transmitting antenna，solar arrays and truss structures，and presented a hybrid high/low band‑width robust controller to alleviate the control-struc‑ture interaction problem.The attitude controllers in Refs.［8-9］were based on the accurate dynamic model of the flexible solar power satellite.Howev‑er，the accurate dynamic model of such ultra-large spacecraft are not easy to established because of the uncertainties of numerous system parameters，clear‑ances of connecters between structural modules，and complicated space perturbations for multiple flexible components.Thus，model-free attitude con‑trollers are appealing for complicated ultra-large space structures.

The attitude control moments of the solar pow‑er satellite are usually periodic due to the periodic or‑bit and attitude［7］.In this case，the iterative learning control（ILC）method is very suitable to improve the control accuracy of current period by studying the control moments from previous periods and us‑ing them as feedforward control moments.ILC was firstly proposed in 1984 to improve the control accu‑racy of the robots performing repetitive opera‑tions［10］.One of the most important advantage of ILC is that it is a model-free control method that can be applied to complicated systems with uncertainties and large amplitude periodic disturbance［11］.In the recent years，ILC has been applied to the control systems in all kinds of engineering［12-13］.Particular‑ly，ILC shows great potential to obtain high-preci‑sion attitude tracking control of satellites［14］.A highorder ILC controller is proposed to obtain precise Sun-facing and Earth-facing attitude control of a multi-rigid-body system of Multi-Rotary Joint Solar Power Satellite［15］.A smooth switch was adopted to avoid the sudden change of control moments，and a filter was used to reduce the influences of measure‑ment noise and non-periodic signals.This method was further applied to a rigid-flexible coupled multi‑body system of Multi-Rotary Joint Solar Power Sat‑ellite［16］.However，the parameters of the controller in Refs.［15-16］must be selected manually based on experiences.The concept of fuzzy logic was intro‑duced to the design of ILC to reduce the number of tuning parameters and improve the convergence and stability of the controller in Refs.［17-18］.

Thus，this paper aims to propose a self-tuning fuzzy ILC to maintain the Sun-facing attitude of a flexible solar power satellite.The rest of this paper is organized as follows.An orbit-attitude-structure coupled dynamic model of the flexible solar power satellite is built in Section 1.The implementation of the proportional-derivative（PD）controller，fuzzy PD controller，and fuzzy ILC controller are present‑ed in Section 2.Section 3 studies the numerical sim‑ulation results of the proposed controllers.Finally，the conclusions are given in Section 4.

1 Dynamic Modeling

A conceptual graph of a solar power satellite［2］in orbit is shown in Fig.1.It consists of an ultralarge solar array，a microwave transmitting anten‑na，a reflector，and other subsystems such as sup‑porting structures.The ultra-large solar array should face to the Sun to capture solar radiation and gener‑ate electricity.This paper focuses on the attitude control of an ultra-large solar array as an example.The main objective is to improve attitude control ac‑curacy while reducing the influences of structural vi‑brations and measurement noise.

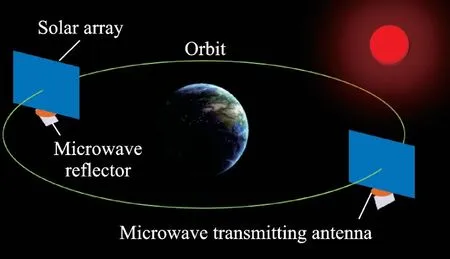
Fig.1 Conceptual graph of a solar power satellite in orbit

The flexible solar power satellite is simplified as a flexible Euler-Bernoulli beam moving in space（Fig.2）.An inertial coordinate systemOXYis con‑structed.PointAand PointBare two endpoints of the beam.The attitude control of the flexible beam is performed using two control moment gyros at PointAand PointB［19］.The control moments are denoted asMAandMB.The attitude control objec‑tive is that the beam remains parallel toOXaxis un‑der the influence of gravity gradient torque.The atti‑tude errors are represented byθAandθB.The param‑eters of the flexible beam model are summarized in Table 1.

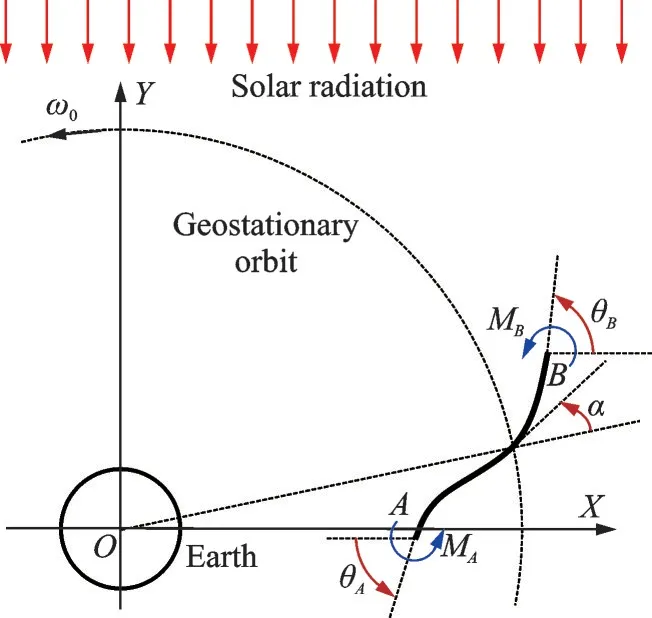
Fig.2 Orbit-attitude-structure coupled beam model

Table 1 Parameters of the simplified beam model

The beam is modeled by absolute nodal coordi‑nate formulation considering the gravitational force and gravity gradient.The absolute nodal coordinate formulation is a well-known rigid-flexible coupled modeling method considering geometric nonlineari‑ty.In this paper，a two-node Euler-Bernoulli beam element is adopted［20］，and a two-dimensional dy‑namic model is established to reduce simulation time while it is able to simulate the orbit-attitudestructure coupled effects.The dynamic equations of the flexible beam can be written as［21］

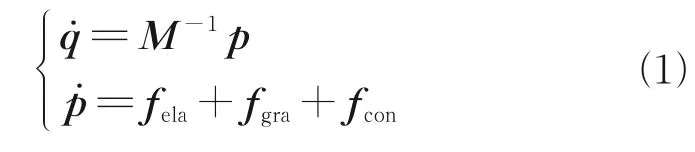
whereqis the generalized coordinate vector，pthe termed generalized momentum vector，Mthe mass matrix，andfela，fgra，fconare the vectors of elastic force，gravitational force（including gravity gradi‑ent），and control force，respectively.The defini‑tion of nodal coordinates as well as the formulas of mass matrix and elastic force can be found in Ref.［20］.The formulation of the gravitational force was given in Ref.［22］.The control force vectorfconcan be obtained by the principle of virtual work.The detailed modeling procedure is not given for simplicity.

The dynamic model in Eq.（1）is an orbit-atti‑tude-structure coupled model.However，the orbital elements，such as the semi-major axis and eccentric‑ity，are not changed in the simulations because the orbital perturbations are not considered.Thus，the orbital results are not given in the following simula‑tions.The attitude motions of the beam（θAandθB）can be calculated from the generalized coordinate vectorq.In the simulations，the attitude motions are coupled with structural vibrations.The attitude disturbance considered in this paper is the gravity gradient torque.However，it is not easy to give the expression of the gravity gradient torque because it is influenced by the structural vibrations.For small deformation cases，the gravity gradient torque can be roughly estimated by

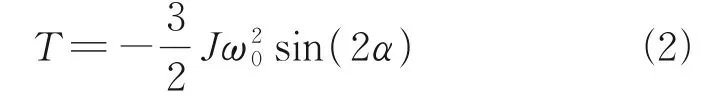
whereJ=is the moment of inertia of the beam，ω0the orbital angular velocity，andαthe atti‑tude angle of the midpoint of the beam shown in Fig.2.

In the following numerical simulations，the beam moves in geostationary orbit（ω0=7.292 123×）.The beam is initially unde‑formed，located at the positiveOXaxis.The initial attitude errors areθA=θB=0 andIn an ideal case，the attitude angleαwould decrease linearlyα=α0-ω0t，andα0=0 is adopted in sim‑ulations.

Based on the above parameters，the maximum control moment is 823.2 N∙m，and the required an‑gular momentum storage is 1.13×107N ⋅m ⋅s.In Ref.［7］，a concept of space-assembled momentum wheel is proposed with a peak angular momentum of 4×108N ⋅m ⋅s and a mass of 6 061 kg，which can be used in the attitude control of the solar array.Alternatively，24 large control moment gyros can be adopted（250 kg and 500 000 N ⋅m ⋅s for each one）［7］.

2 Control System Description

This section presents the implementation of the proposed self-tuning fuzzy ILC method.The atti‑tude control objective isθA=θB=0 such that the beamABfaces to the Sun.In practice，the attitude anglesθAandθBshould be measured by attitude sen‑sors（such as Star trackers and Sun sensors）and then estimated using attitude filtering methods（such as extended Kalman filter approach）.Howev‑er，the attitude anglesθAandθBare simply calculat‑ed from the generalized coordinate vectorqin nu‑merical simulations because attitude estimation is not the focus of this paper.

2.1 PD control

The control moments of the classic PD control law are calculated by

wherekdandkpare the proportional and derivative feedback gains.The feedback gains are designed by

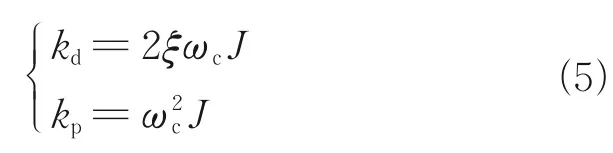
whereωcis the designed control frequency，andξ=0.7 the designed damping ratio of the controller.Al‑though the PD control is a model-free control meth‑od，the control frequency should be selected manual‑ly.For a more complicated system such as the Multi-Rotary Joint Solar Power Satellite，the con‑trol frequencies for 50 solar arrays must be selected independently because of the different stiffness of the trusses［16］.

2.2 Fuzzy PD control

In this subsection，a self-tuning fuzzy PD con‑trol method is studied for the flexible beam，based on the Mamdani fuzzy system.The objective of the fuzzy system is to select a minimum control frequen‑cy while meeting the control accuracy requirement.The fuzzy system is applied toMAandMBindepen‑dently.The design process of the fuzzy controller in‑cludes fuzzification，rule-based inference，and de‑fuzzification.For details of fuzzy control，please re‑fer to Ref.［23］.

Firstly，the function of the fuzzy system is to change the control gains according to the control er‑ror.In many fuzzy controllers，the fuzzy system works continuously using the real-time control er‑ror，which leads to frequent change of the control gains.To avoid this problem，the fuzzy system works once every half orbital period in the proposed fuzzy PD controller，because the period of the gravi‑ty gradient torque is half an orbital period as shown in Eq.（2）.In other words，the control gains are ad‑justed every half orbital period according to the aver‑aged control error.Therefore，the input of the fuzzy system is

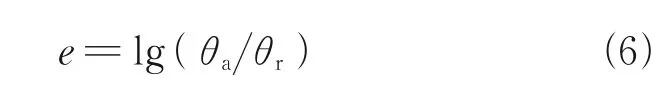
whereθais the average absolute value of the attitude error within half an orbital period，andθra reference value ofθa.The attitude control accuracy require‑ment is 0.5°，and the control error is usually a trigo‑nometric function of time because the gravity gradi‑ent torque is also a trigonometric function of time，as shown in Eq.（2）.Then，θashould be less than 0.32°，and the value ofθris selected as 0.32°.The difference betweenθaandθris always within two or‑ders of magnitude.Thus，the input domain can be taken as［-2，2］.

The control frequency is adjusted by

whereωc1andωc2are the control frequencies before and after the action of the fuzzy system，andkis the adjustment parameter（also the output of the fuzzy system）.The value ofkdetermines the variation speed of the control frequency.The domain ofkin this paper is[-0.5，0.5].The use of logarithmic and exponential scale in Eqs.（6）and（7）enables the fuzzy system to handle a wide range of input and out‑put.

Triangular membership functions for both input and output variables are employed，as shown in Fig.3 and Fig.4.In the membership distribution，the fuzzy variables are labeled with“N”“ZO”and“P”to represent“negative”“zero”and“positive”，respectively.And the labels“B”“M”and“S”mean“big”“medium”and“small”，respectively.

Fig.3 Membership function of input

Fig.4 Membership function of output

The rule-base inference is the key step for the fuzzy system design.According to the experience of attitude control of a flexible beam considering gravi‑ty gradient，the control errors decrease monotonous‑ly with the control frequency.Whenθais larger thanθr，ωcneeds to be increased.Therefore，a simple fuzzy rule can be established，as shown in Table 2.A rule in Table 2 can be interpreted as“If the input is NB，then the output is NB”.The fuzzy system can adopt multiple inputs and multiple outputs ac‑cording to practical requirements.The centroid for‑mula is employed for defuzzification［23］.Combined with the input and output domains，a rule in Table 2 is interpreted as“Ifθa=100θr，thenωc2=The input domain should cover the concerned range of the attitude error.Then，the output domain should be determined by the desired variation speed of the control frequency.In the implementation of the fuzzy PD control，the direct change ofωcby Eq.（7）will lead to drastic changes in control moments.Therefore，a trigono‑metric function is adopted to change the control fre‑quency smoothly.The transition time is 0.25 orbital periods，which is a half of the working period of the fuzzy system.The transition function is

Table 2 Fuzzy rule

whereT=86 164 s is an orbital period andidenotes theith orbital period.

2.3 Fuzzy ILC

Although the fuzzy PD control is able to adjust the control frequency according to the control error，it is a pure PD controller when the control frequency is converged to a certain value.The main problem of the PD controller is that the control moments are proportional to the control errors and the deriva‑tives.The control errors can be reduced only if the control gains are increased.However，the influenc‑es of measurement noise are also increased.

In this section，a fuzzy ILC controller is pro‑posed to improve the control accuracy by not in‑creasing the control gains.The control moment of the ILC with a smooth switching parameter is calcu‑lated by［16］

whereKFFis a switching parameter，Γ=[kp，kd]the matrix of feedback gains andθ=the vec‑tor of control errors.For the first three periods，KFF=0 and the controller is a fuzzy PD controller.At the end of the 3rd period，the controller gradual‑ly becomes an ILC controller that use the control moments of the last period as feedforward control moments.Thus，the switching parameter is de‑signed as［16］

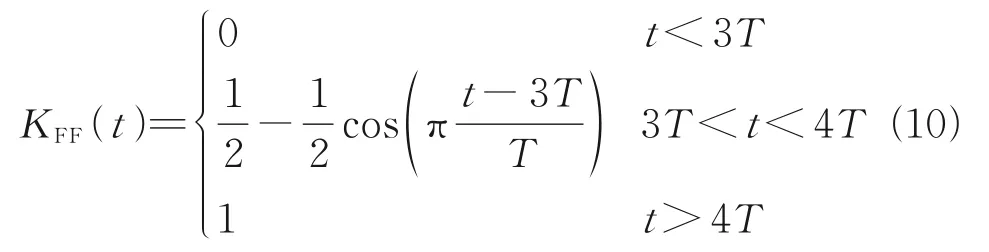
The reason to use fuzzy PD controller in the first three periods is that the control moments of the“previous”period are unavailable for the first peri‑od.Moreover，the fuzzy PD controller can reduce the initial attitude errors and provide more accurate feedforward control moments by adjusting the con‑trol frequencies in the first three periods.

It can be seen in Eq.（9）that the control mo‑ments of the last period is used directly to the cur‑rent period ifHowever，the control moments of the last period contains oth‑er useless signals such as measurement noise and structural vibrations.Thus，the Fourier series is ad‑opted to filter out useless historical signals based on the knowledge of gravity gradient torque，andis calculated by［16］

where

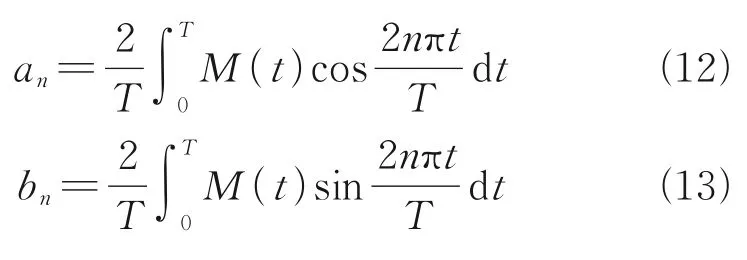
The value ofNcan be selected according to the complexity of the attitude disturbance.In this pa‑per，N=10 is selected because the gravity gradient torque in Eq.（2）is a simple sinusoidal function of time.The control gains are calculated by Eq.（5），and the control frequency is also adjusted by a fuzzy system.Thus，Eq.（9）is a fuzzy ILC controller.

When the controller is switched form fuzzy PD control to fuzzy ILC，the control errors would de‑crease significantly.The input domain of the fuzzy system can be expanded to [-3，3] to avoid the in‑put overflow of the fuzzy system，because the actual attitude errors might become three orders of magni‑tude smaller than the reference value.Other parame‑ters of the fuzzy system are unchanged.In addition，since the control accuracy of ILC is much higher than the prescribed errorθr，the fuzzy system tends to reduceωcto the maximum extent.However，the attitude of the flexible beam is unstable whenωcis too small.Therefore，ωcshould not be less than an allowed minimum control frequency 1×10-4in the simulation program by

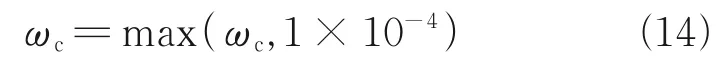
Alternatively，the allowed minimum control frequency can be selected by another fuzzy system，which could be studied in future works.

3 Simulation Results

Measurement noise is considered in the follow‑ing simulations.Gaussian white noise is used in the simulation program with an overall amplitude of 4×10-4rad for attitude angle andfor an‑gular velocity.

3.1 PD control

Firstly，the control results of the PD controller are studied for different control frequencyωc，which varies from 5×10-5to 5×10-3.Simulation results are shown in Figs.5—7.It can be seen that due to the influence of periodic gravity gradient torque，the Sun-facing attitude errors and control moments of the PD controller also vary periodically.The maxi‑mum gravity gradient torque calculated using Eq.（2）is 823.2 N ∙m.The variations of the control moments in Fig.6 shows good agreement with theo‑retical results in Eq.（2），as the gravity gradient torque is counteracted byMA+MB.Whereas，the maximum value ofMA+MBis 1 322 N ∙m，which indicates that measure noise has great influences on attitude control moments.With the increase ofωc，the maximum errorsθmaxdecreases significantly.Thus，the control accuracy of the PD controller can be increased by increasing the feedback control gains.However，larger control gains also lead to more serious influences of measure noise on control moments.

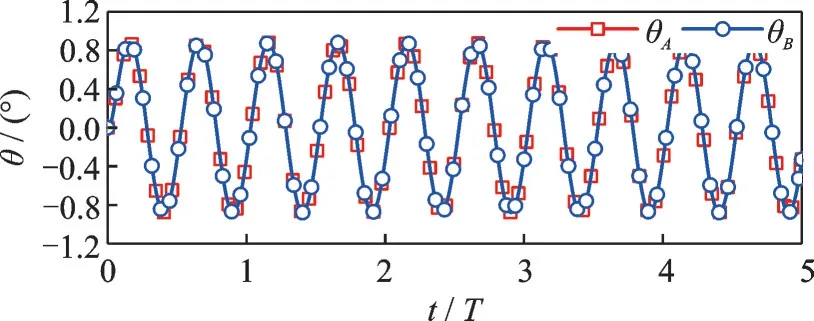
Fig.5 Errors of the PD control(ωc=5×10-4)

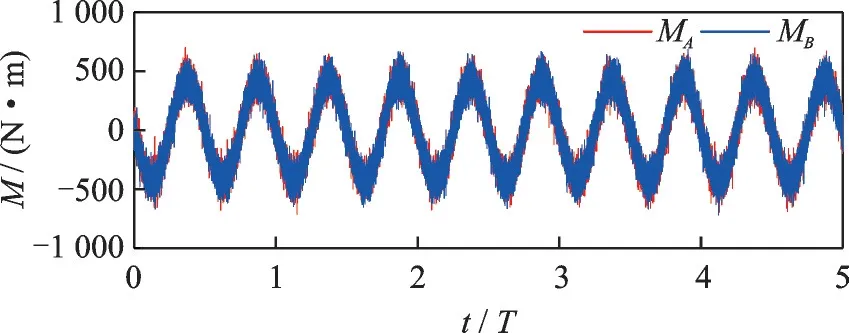
Fig.6 Moments of the PD control(ωc=5×10-4)

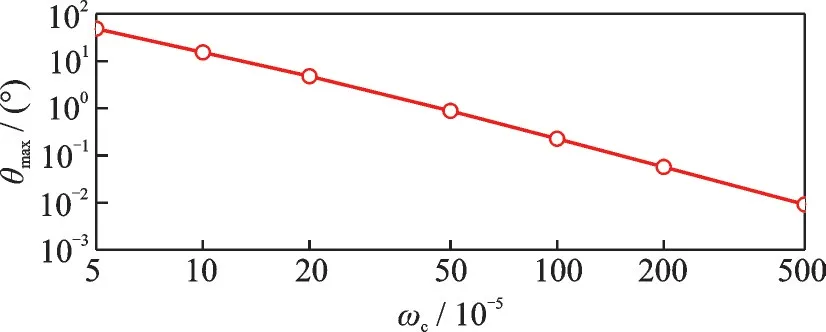
Fig.7 Maximum control errors for different control frequen‑cies

3.2 Fuzzy PD control

A numerical simulation is conducted with an initial control frequency ofωc0=5×10-5using the fuzzy PD controller.Simulation results are shown in Figs.8—10.At the beginning of the simulation，the control errors increase greatly because of the low control frequency.Then，the control frequency is in‑creased by the fuzzy system，and finally converges to a value that the maximum control errors are ap‑proximately 0.5°.It can be seen in Fig.10 that the control frequency is adjusted every half orbital peri‑od by the fuzzy system.Moreover，the control fre‑quency is changed smoothly during 0.25 orbital peri‑od.The influences of measurement noise are also in‑creased as the control gains increase.

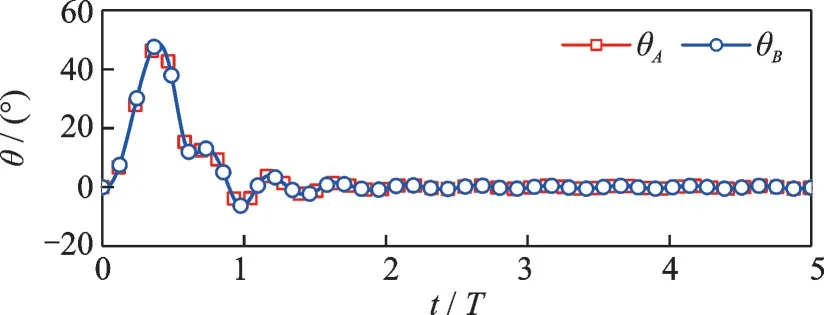
Fig.8 Errors of the fuzzy PD control (ωc0=5×10-5)

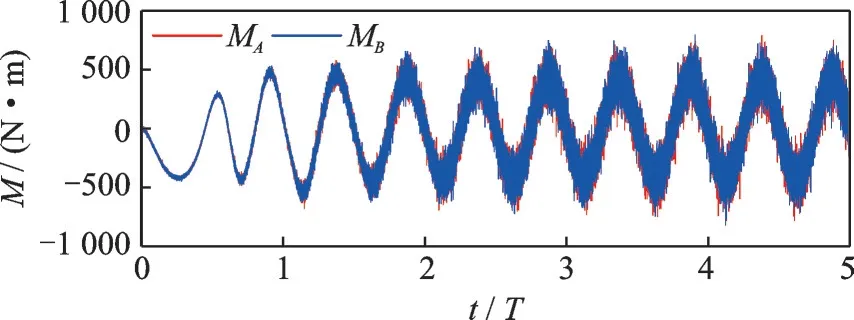
Fig.9 Moments of the fuzzy PD control (ωc0=5×10-5)

Fig.10 Control frequency of the fuzzy PD control (ωc0=5×10-5)

Another numerical simulation is carried out us‑ing a larger initial control frequencyωc0=2×10-3，as shown in Figs.11—13.At the beginning of the simulation，the control errors are small and the con‑trol moments are large.The measurement noise af‑fects the control moments seriously.As the fuzzy system works，the control frequency and control moments are reduced gradually，while the control errors meet the control accuracy requirement.The control frequency converges to almost the same val‑ue as Fig.10.Thus，the fuzzy PD controller is able to achieve the required attitude control accuracy and adjust the control gain approximately.

However，the measurement noise has great in‑fluences on the control moments.The maximum values ofMA+MBof the last period in Fig.9 and Fig.12 are over 1 360 N ∙m，which are much larger than the maximum value of gravity gradient torque（823.2 N∙m）.The reason is that the control accura‑cy and the influence of measurement noise are both proportional to the feedback gains，because the fuzzy PD controller becomes a pure PD controller when the control frequency is converged.Thus，the fuzzy ILC is proposed to improve control accuracy without increasing the feedback gains.

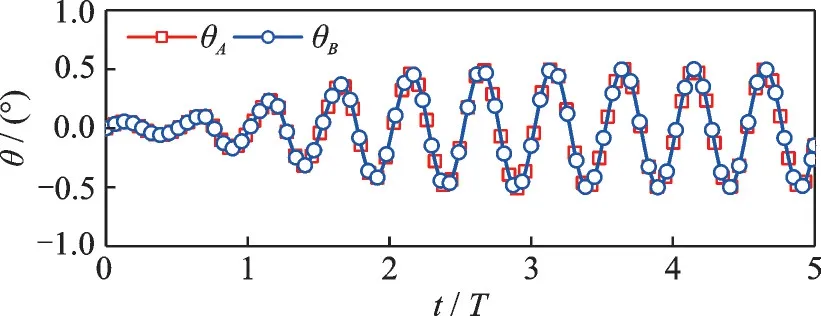
Fig.11 Errors of the fuzzy PD control (ωc0=2×10-3)

Fig.12 Moments of the fuzzy PD control (ωc0=2×10-3)

Fig.13 Control frequency of the fuzzy PD control (ωc0=2×10-3)

3.3 Fuzzy ILC

The fuzzy ILC is adopted in the numerical sim‑ulation，and the initial control frequency isωc0=5×10-5.Simulation results are depicted in Figs.14—16.In the first three periods，the controller is a fuzzy PD controller，and the results are the same as Figs.8—10.Whereas，when the fuzzy ILC is gradu‑ally switched on after three periods，the control er‑rors are further decreased by using the control mo‑ments of last period as feedforward control mo‑ments.Consequently，the control frequency can be reduced by the fuzzy system.Moreover，the influ‑ences of measurement noise on the control moments are greatly reduced after the 4th period.The control frequencyωcbecomes 1×10-4after six periods to ensure the attitude stability of the system.

The simulation with a large initial control fre‑quencyωc0=2×10-3is also investigated，as shown in Figs.17—19.In the first three periods，the control frequency decreases under the effect of the fuzzy system because the control errors are very small.Thus，the control errors increase.As the con‑troller is switched to the fuzzy ILC after three peri‑ods，the control errors，control frequency，and the influences of measurement noise are reduced signifi‑cantly.The maximum values ofMA+MBof the last period in Fig.15 and Fig.18 are less than 898 N ∙m.And the maximum attitude errors of the last period in Fig.14 and Fig.17 are less than 0.01°.Thus，the advantages of the proposed fuzzy ILC are small atti‑tude control errors，small control moments，and self-tuning ability.The proposed controller can also be applied to the attitude control of large transmit‑ting antenna in addition to the solar array，because the transmitting antenna requires 0.01° attitude accu‑racy.

Fig.14 Errors of the fuzzy ILC (ωc0=5×10-5)

Fig.15 Moments of the fuzzy ILC (ωc0=5×10-5)

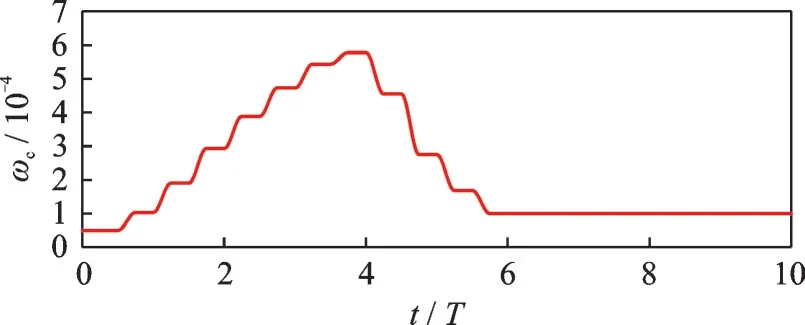
Fig.16 Control frequency of the fuzzy ILC (ωc0=5×10-5)

Fig.17 Errors of the fuzzy ILC (ωc0=2×10-3)

Fig.18 Moments of the fuzzy ILC (ωc0=2×10-3)

Fig.19 Control frequency of the fuzzy ILC (ωc0=2×10-3)

The structural vibrations of PointBof the beam using fuzzy ILC withωc0=2×10-3are shown in Fig.20.The structural vibration of PointBis estimated using a local coordinate system fixed at PointA.Structural vibrations are induced by the dis‑tributed gravity gradient and control moments.It can be seen that the structural vibration amplitudedis less than 0.4 m，which is very small compared to the length of the beam.

Fig.20 Structural vibration of Point B using fuzzy ILC(ωc0=2×10-3)

3.4 Influences of structural vibrations

This subsection studies the validity of the pro‑posed self-tuning fuzzy ILC for different system pa‑rameters.Particularly，when the Young’s modulus is very small，the beam is extreme flexible and the gravity gradient could induce large-amplitude struc‑tural vibrations.Then the structural vibrations could greatly affect the attitude control accuracy.Thus，the Young’s modulus is selected asE=0.23 GPa andE=2.3 GPa in the simulations，oth‑er parameters are not changed.The attitude control‑ler is fuzzy ILC with initial control frequency ofωc0=2×10-3.Numerical results are depicted in Figs.21—24.

Fig.21 Errors of the fuzzy ILC with small Young’s modu‑lus (ωc0=2×10-3)

Fig.22 Moments of the fuzzy ILC with small Young’s mod‑ulus (ωc0=2×10-3)

Fig.23 Control frequency of the fuzzy ILC with small Young’s modulus (ωc0=2×10-3)

It can be found that the control errors of PointAare much larger than the above cases forE=230 GPa in Fig.14 and Fig.17.However，the maxi‑mum attitude errors in the last orbital period are 0.56°forE=0.23 GPa and 0.20°forE=2.3 GPa.The attitude error is just slightly larger than the re‑quired control accuracy for the extremely flexible beam.This problem can be solved by increasingθrslightly and performing structural vibration control of the beam［24］.In terms of control moments，the control moments forE=0.23 GPa is greatly influ‑enced by structural vibrations.The maximum val‑ues ofMA+MBin the last period are 2 713 N∙m forE=0.23 GPa and 978 N∙m forE=2.3 GPa.More‑over，the influences of measurement noise on the control moments are reduced dramatically forE=2.3 GPa.The control frequency forE=0.23 GPa is much larger than other cases，and it is not con‑verged to a certain value at the end of the simula‑tion.In contrast，the control frequency forE=2.3 GPa becomes 1×10-4after eight orbital peri‑ods.It can be seen in Fig.24 that the maximum structural deformations are 825 m forE=0.23 GPa and 41.6 m forE=2.3 GPa.In summary，the pro‑posed fuzzy ILC is validated to obtain the prescribed attitude control accuracy even if the beam is ex‑tremely flexible.

Fig.24 Structural vibration of Point B using fuzzy ILC with small Young’s modulus (ωc0=2×10-3)

4 Conclusions

A self-tuning iterative learning control method is proposed for the attitude control of a flexible solar power satellite.The control frequencies of the PD control and ILC methods are adjusted automatically based on fuzzy logic.Although some parameters have to be selected for the proposed controller，such as the input/output domains and the transition time of the control frequency，they only affect the adjust‑ing process of the control frequency，instead of the adjusting result.Thus，they are not required precise‑ly.The main conclusions of this paper are as fol‑lows.

（1）The control frequency of the fuzzy PD con‑troller is adjusted to a suitable value that the control errors are not larger than the prescribed error.

（2）The control errors are reduced greatly when the controller is switched from fuzzy PD con‑trol to fuzzy ILC.

（3）The influences of measurement noise are reduced as the decrease of the control frequency of the fuzzy ILC.

（4）The adjustment process is smooth by using the trigonometric function when changing the con‑trol frequency，so that the sudden changes of con‑trol moments are avoided.