基于高斯过程的倾转旋翼机器人模型辨识

霍雨佳，李一平，封锡盛

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁沈阳 110016;2.中国科学院机器人与智能制造创新研究院，辽宁沈阳 110169;3.辽宁省水下机器人重点实验室，辽宁沈阳 110169;4.中国科学院大学，北京 100049)

0 前言

倾转旋翼水空跨域机器人(以下简称跨域机器人)，充分结合了水下机器人(AUV)的隐蔽性和无人机(UAV)的机动性，具备水空两栖多种介质下的作业能力，扩展了原有机器人的作业环境和应用范围。跨域机器人应分别具备在水中、空气中两种介质中稳定工作，同时具备水空两种介质间多次反复跨介质转换的能力。由于两种工作介质在密度等方面的显著区别，跨域机器人在多种介质中稳定的作业需求对机器人的运动控制器提出了艰巨的挑战。因此，针对跨域机器人，建立可靠的动力学模型是设计机器人运动控制器的关键。

模型辨识方法在水下机器人和无人机上都有广泛应用，辨识数据来源于机器人传感器的数据采集，将所获的动力学模型用于机器人运动控制仿真平台搭建和控制策略设计。最小二乘法、极大似然等参数化建模方法，需要一定的先验知识，如机器人的动力学模型结构，可由流体力学、惯性和结构布局等分析得到。所获得的高精度模型常限制在一个小范围内，通常通过增加建模的复杂性提高模型的范围。利用神经网络、示教学习等非参数化建模也可获得一定的效果，但所构建的模型被限制在受过训练的集合内，难以应对模型的不确定性。

高斯过程回归(Gaussian Processes Regression,GPR)是基于贝叶斯理论和统计学习理论的一种机器学习方法，适于处理小样本、非线性等复杂问题，被广泛应用于机器人等领域。该方法提供了一种简单有效的方式表示数据的先验分布，可使用较少的参数得到准确的模型。GPR属于非参数模型，只需假设它服从指定均值函数和协方差函数的高斯过程。相较于其他常用的参数模型，如神经网络、支持向量回归、多项式回归等，GPR具有易训练、超参数自适应获取以及预测结果具有概率意义等特点。KO等利用高斯过程(Gaussian Processes,GP)模型和强化学习实现对飞艇的模型辨识和运动控制。FU等利用高斯过程实现对船舶模型的辨识。HEMAKUMARA和SUKKARIEH利用GP模型对固定翼UAV的模型进行辨识，获得了固定翼机翼模型。CAO等利用GP模型和MPC控制器实现四旋翼无人机的运动控制仿真。

本文作者利用高斯过程对跨域机器人的动力学模型进行辨识。通过采集遥控飞行过程中机器人的状态数据，获得机器人的动力学模型。这种非参数化建模方法可利用机器人运行过程中的反馈数据较大范围地获取机器人的动态特性，而不需要对机器人的模型结构具备先验知识，可以在控制器设计环节节省大量试验成本。

1 跨域机器人动力学模型分析

为实现对跨域机器人的动力学模型进行辨识，应对机器人进行模型分析。本文作者采用一种新型跨域机器人，具有4台水空两栖涵道推进器，如图1所示。如图1(b)所示，4台推进器可以旋转的最大角度为π/2，可实现推进器推力由向下到向后的切换。

该跨域机器人具备水下航行、水面滑行起飞、水面(陆地)垂直起飞悬停和空中平飞等工作模式。其中，在垂直起飞悬停模式下，推进器推力向下，机器人以旋翼飞行器模式工作；在空中平飞状态下，机器人以固定翼飞机模式工作，通过升力体机翼提供机器人升力，通过控制涵道推进器倾转角度和螺旋桨转速控制机器人的俯仰。

机器人载体坐标系选择重心为原点，遵循右手系，指向前方并与机器人纵向对称轴重合;位于机器人水线面,与垂直并指向右舷;位于机器人纵中剖面,与垂直并指向下，如图1(a)所示。

图1 倾转四旋翼跨域机器人

本文作者主要考虑机器人以倾转旋翼模式在空中飞行时的运动控制问题。机器人在飞行中受力主要分为涵道推进器推力、机翼升力与阻力、重力和机身阻力。上述力会同时对机器人产生相应的力矩，同时涵道推进器桨叶的旋转也会产生相应的力矩。

由文献[16-17]可知，令=[,,]表示载体坐标系下机器人在横滚、俯仰和偏航方向的角速度，=[,,]表示机器人姿态角，=[,,]表示载体坐标下机器人各方向线速度，=[,,]表示世界坐标系下机器人位置,则跨域机器人的动力学模型可描述为

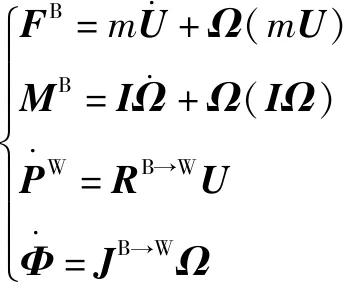
(1)

其中:=[,,}为载体坐标系下机器人各方向分力；=[,,]为载体坐标系下机器人绕各轴力矩;为载体坐标系到世界坐标系的旋转矩阵；为载体角速度到姿态角速率的旋转矩阵。则世界坐标系下，机器人的受力可描述为

(2)

跨域机器人的4个涵道风扇推进器产生的合外力为

(3)

其中：T,、T,和T,分别表示合力在载体坐标系下、和轴上的分量，有：

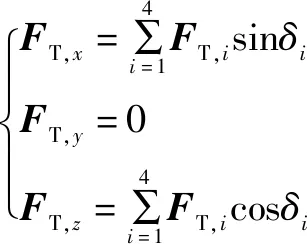
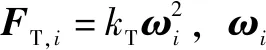
同时，推进器推力产生的力矩为

T,=T,

(4)

式中：表示第个推旋翼进器中心距离重心的距离，表达式为

(5)

其中：,为第个倾转旋翼推进器轴中心到机体坐标系下平面的距离；,为倾转旋翼推进器轴中心到机体坐标系平面的距离；为推进器旋翼中心到倾转轴的距离。

2 基于高斯过程回归的跨域机器人动力学预测模型

2.1 高斯过程回归模型

(6)

(7)

其中:(,)为通过所有数据集输入计算得到的协方差矩阵;为单位矩阵。输出数据集和对问询点的预测输出()的联合分布为

(8)

其中:()的条件分布服从一个新的正态分布：

(|,)～[(),()]

(9)

则()的均值和方差的表达式为

(10)

()=(,)-(,)((,)+

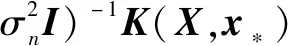
(11)

因此，计算预测点的预测值可得：

=(,)

(12)

同时，采用平方指数协方差函数作为GPR的内核函数(,)：

(13)

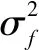
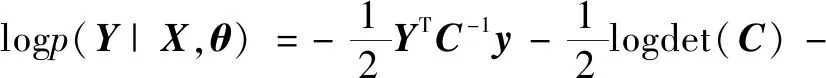
(14)

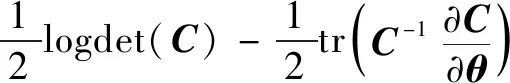
(15)

则GPR模型的优化目标为

=argmin()

(16)

对超参数进行迭代更新以最小化()。最后将优化后的超参数代入式(10)和式(11)得到测试样本最终的预测值和方差()。

2.2 基于权值的局部高斯过程回归模型

由于高斯过程回归在输入训练集较大时计算缓慢，为降低其模型回归过程中的计算复杂度，提出采用局部高斯过程回归方法。该方法通过引入多个局部模型，将训练集分配到多个局部模型中进行单独训练，由此减少每个局部模型的数据量和总体的计算复杂度。因此，该方法可以保证模型的快速更新。

通过计算新的训练数据与模型中心的距离，对数据进行分配，该距离可描述为

(17)

同时，设置阈值，判断它是否属于已有的局部模型。当数据不属于已有的任一局部模型时，则以此数据建立新的局部模型。局部高斯过程回归流程如图 2所示。

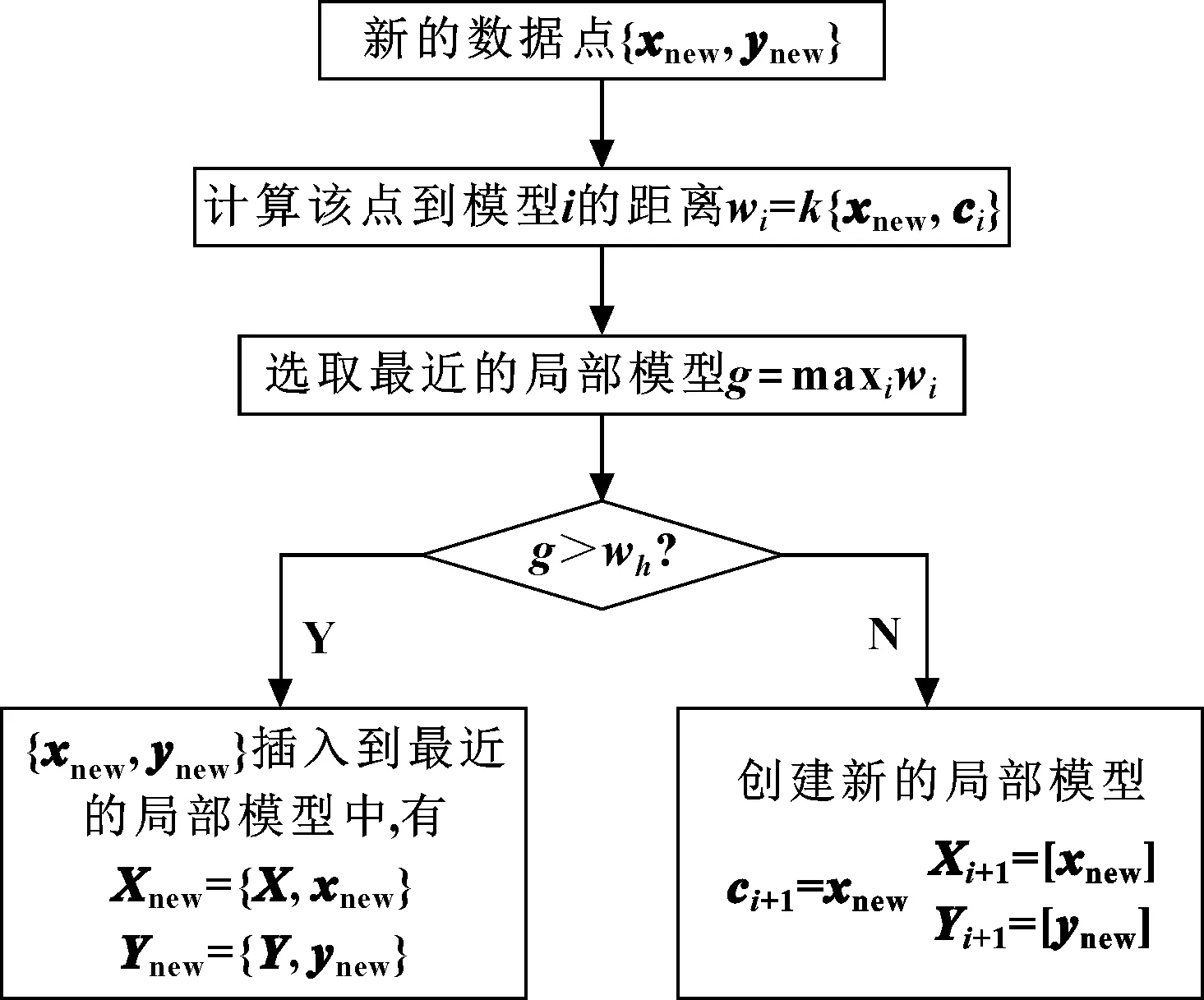
图2 局部高斯过程回归流程

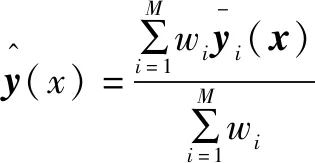
(18)

3 验证

3.1 试验设计

基于新型水空跨域机器人，考虑当前机器人以倾转旋翼无人机模式进行飞行(空中悬停)的情况，通过遥控器控制机器人的飞行。机器人的输入为其8个执行机构的动作量，包括4台涵道螺旋桨的转速(=1,2,3,4)和4台倾转舵机的倾转角度(=1,2,3,4)。机器人的传感器如IMU和GPS获得机器人的运动状态包括位置信息、姿态信息、速度和角速度信息等。

如图 3所示，机器人控制模块主要由PX-4控制板构成，PX-4主要承担通信、数据记录功能，与无线遥控器实现通信并下发指令。同时，利用它自带的简单的倾转旋翼机器人控制算法，实现简单的机器人飞行控制试验，以获取机器人的运动状态数据。机器人通过外接的60 V直流电源通电。

图3 试验平台构成

对于时刻，基于高斯过程的机器人动力学模型辨识有：

(19)

(20)

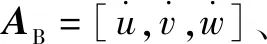
3.2 试验

机器人的输入包括执行机构控制量和机器人的速度和姿态等信息。同样的，在相同的执行机构中控制输入，利用第2.2节方法，获得机器人的动力学模型。并对比相同控制输入下的模型预测值和实际测量值。

图4 模型预测与实际测量值对比

定义平均绝对值误差(Mean Absolute Error,MAE)评价模型预测精度，如式(21)所示。同时，对比全局GPR和LGPR的更新时间和预测时间，评价两种方法在计算复杂度上的区别，结果如表1所示。

表1 全局GPR和LGPR性能评价

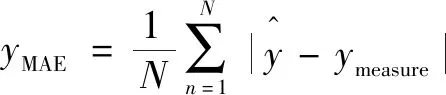
(21)

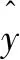
4 结论

本文作者提出了一种基于高斯过程的辨识方法，采用该方法实现对新型跨域机器人在空中以倾转旋翼无人机模式下飞行的动力学模型辨识。通过试验，对比了测量值和模型预测值，证明了该方法的有效性。该模型为跨域机器人仿真平台及其运动控制器设计提供了参考，同时后续应完善机器人的功能(如空中平飞和水下航行等)，实现对机器人更多模式下的动力学模型辨识。