基于键合图和贝叶斯网络的NPC逆变器故障诊断

程硕，帕孜来·马合木提

(新疆大学电气工程学院，新疆乌鲁木齐 830047)

0 前言

相比于传统的两电平逆变器，多电平逆变器具有输出电压高、谐波含量比较低、电压容量高等优点，被广泛应用于各种牵引拖动系统。随着电平数增加，逆变器的功率开关管数量增多，故障率也随之升高。逆变器发生故障时，其输出电压波形畸变、直流侧电压不平衡甚至停机。因此，对三电平逆变器故障进行及时诊断，对提高系统安全性、可靠性有重要意义。

文献[3]和文献[4]分别从电流残差和电流矢量变换两个角度对逆变器进行故障诊断，利用电流残差诊断方法，可以快速诊断单管开路故障，但是所提出的混杂系统建模过程比较复杂且诊断精度受负载变化的不确定性影响较大；电流矢量变换诊断方法具有诊断效率高的优点，但是其准确率受故障阈值选取的不确定性影响很大。文献[5]通过三相电流的傅里叶变换，将时域信号转化为频域，提取其直流分量、基波幅值、基波相位以及二次谐波相位等频域特征，构建故障特征向量，输入神经网络进行诊断。但是，在傅里叶变换的同时，也丢失了信号的时域特性。文献[6]将小波分析与粒子群优化的支持向量机结合起来，诊断了三电平逆变器的开路故障,但是小波函数选取的不确定性会影响诊断结果。有学者利用专家系统进行诊断，但建立一个完备的专家系统需要大量领域专家的经验知识，且维护难度大。

基于以上问题，本文作者提出一种键合图建模和贝叶斯网络定量分析方法。贝叶斯网络适用于表达和分析不确定性事物，并通过对未知信息的推理估计，得到故障发生的概率。与传统的故障诊断方法相比，这种概率推理方法在诊断过程中充分表达和分析了系统的不确定性。有专家提出通过数据学习来构建贝叶斯网络，但是构建的网络受数据影响较大，数据的不完备性和不确定性会影响网络的构建。键合图建模过程简单，不需要大量的专家经验知识和数据，通过模型可以直观了解系统的结构。因果路径分析可以了解隐藏在模型内部的键合图元件之间的因果关系，进而了解系统的运行机制。

因此，本文作者先搭建系统的键合图模型，由键合图模型的因果路径和贝叶斯网络中因果关系的相似性，构建系统的贝叶斯网络模型进行故障诊断。贝叶斯网络诊断不仅可以定位故障元件，还可以计算出故障元件对系统的影响程度。

1 建模与诊断理论分析

1.1 贝叶斯网络推理分析

贝叶斯网络的理论基础为概率统计学中的贝叶斯定理，以概率图论为模型，其计算方法明确、推理过程严谨，可以应用于多个研究方向。

贝叶斯网络的推理有2种形式：正向推理和反向推理。正向推理即根据根节点的先验概率和节点间的条件概率，计算网络中任意节点的概率。反向推理则是根据观测变量集合，计算目标集合的后验概率分布()。

在贝叶斯网络中，=(,,…,)表示一组事件，为事件指向的节点，则是节点的父节点。贝叶斯网络的正向推理过程为

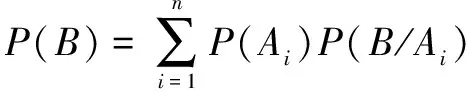
(1)

其中：、为节点；()为节点的条件概率。

在节点发生的条件下，父节点的后验概率为

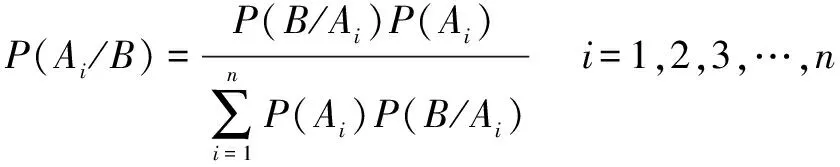
(2)

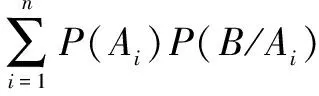
重要度是指系统中单个或多个事件发生故障或状态改变时对系统的影响程度。贝叶斯网络中的根节点对系统中故障的敏感程度，可以通过分析贝叶斯网络的灵敏度得知。当根节点的故障发生较小程度的变化时，叶节点的故障发生较大的变化。

根节点的概率重要度为

显然，p的值越大，相应地pc1、pc2、pc3、pc4的值越小，充电成功的可能性越大。下文将针对各参数大小对充电过程性能的影响进一步分析。

(3)

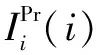
根节点状态为单独引起叶节点故障状态为的关键重要度为

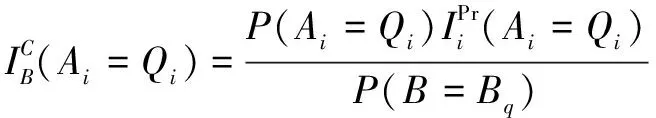
(4)

根节点对于叶节点故障状态为的关键重要度为

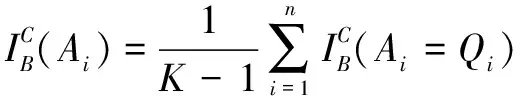
(5)

根节点故障状态为时，叶节点故障状态的灵敏度为

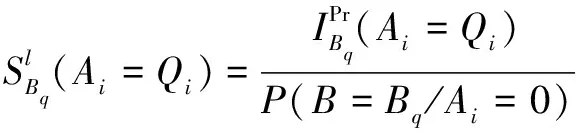
(6)

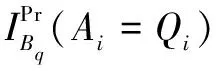
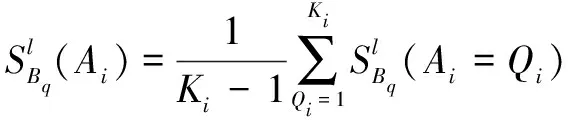
(7)

1.2 键合图中因果关系分析

键合图是一种以图形化的方式描述系统结构的多能域系统建模方法。此方法不仅可以让人清晰直观地了解系统内部各部分元件间的影响关系，还详细地描述了系统内部元件状态的变化过程。键合图模型与现实中物理模型存在着对应关系，同时键合图元件间也有着明确的因果关系。与传统的建模方法相比，基于键合图的方法可对系统内部元件状态的变化过程、变量间的关联与影响等有更直观的了解。因此，利用键合图对中点钳位型三电平逆变器(NPC)进行建模是一种较好的方法。基本键合图元件的因果关系如表1所示。

表1 基本键合图元件因果关系

1.3 时间因果图和故障树分析

故障树分析法是一种自上而下的逐层推理方法，用图形化的方式展现系统所有可能发生的事件。该法将系统中发生的关键故障事件作为顶事件，将逻辑因果关系以倒立树状图形式来表示，向下逐渐找出引起顶事件发生的全部原因。

键合图元件的因果关系各不相同，元件越多，0节点和1节点越多，系统的因果关系就越复杂，很难找全系统的因果关系。时间因果图是一种有向图，用来描述系统内部变量的时间约束关系，并以此来描述系统的动态行为。其中，系统的变量用节点来表示，箭头表示变量之间的因果关系，标号代表其代数关系或积分、微分等。时间因果图分析有前向推理和逆向推理两种，逆向推理可以得到系统异常观测的故障源集合即故障原因。

2 建立NPC逆变器故障树和贝叶斯网络模型

以NPC逆变器系统为研究对象，如图1所示，验证基于键合图和贝叶斯网络的NPC逆变器诊断的有效性。利用节点法思想，搭建NPC逆变器的键合图模型，以A相为例，建立如图2所示的键合图模型，验证其输出波形,如图3所示。针对该键合图模型转化为贝叶斯网络模型的步骤如下：

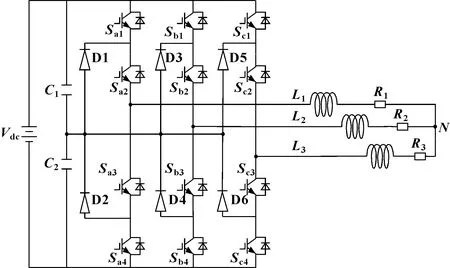
图1 NPC逆变器电路

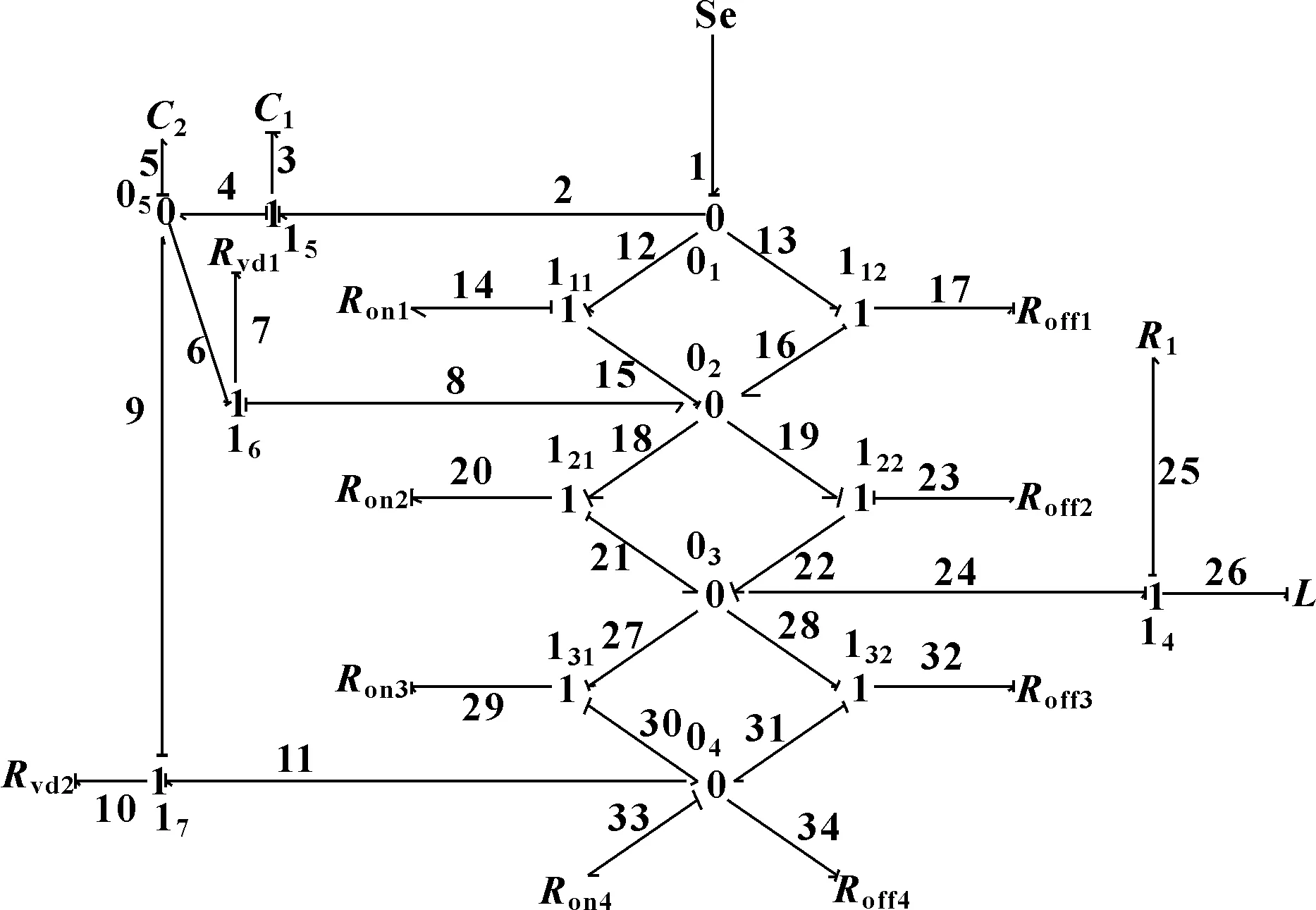
图2 NPC逆变器A相键合图模型

图3 NPC逆变器键合图模型输出波形

首先，列写出键合图模型中每个键合图元件和节点的输入输出关系和因果关系方程，因变量作为输入变量位于方程的右边，果变量为输出变量位于方程的左边，如表2所示。

表2 键合图各节点方程

确定系统各元件的参数为假设变量，将键合图可测的节点作为信息变量，假设变量为故障原因，信息变量为故障结果。

根据各个节点元件的方程推导系统的时间因果图，如图4所示。时间因果图构造步骤如下：先将得到的方程的势变量和流变量按行依次摆放，所有的势变量放一行，流变量放一行；再将所得的方程，用箭头连接等式左右两边的势变量和流变量并标注变量间的关系，箭头由方程的右边变量指向左边变量，对于连等式方程，取最右边的一个为输入变量。

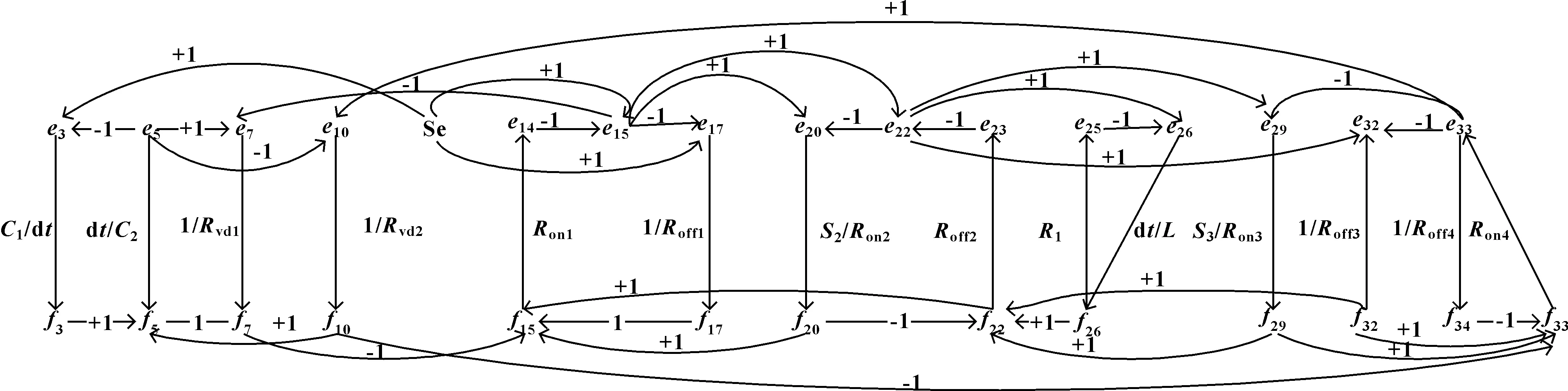
图4 时间因果图模型

再根据推导的系统的时间因果图，采用因果图逆向推理法来推导引起节点(桥臂中点电压)异常的故障集合，所有的故障集合推导完毕后，构建系统的故障树模型。该系统的故障树模型可以分为两个部分，第一部分为节点的故障树推理模型，另一部分为节点的故障树推理模型。推理过程中将节点作为故障树模型的顶事件，系统的故障树模型如图5所示。最后将系统的故障树模型，转化为贝叶斯网络模型。

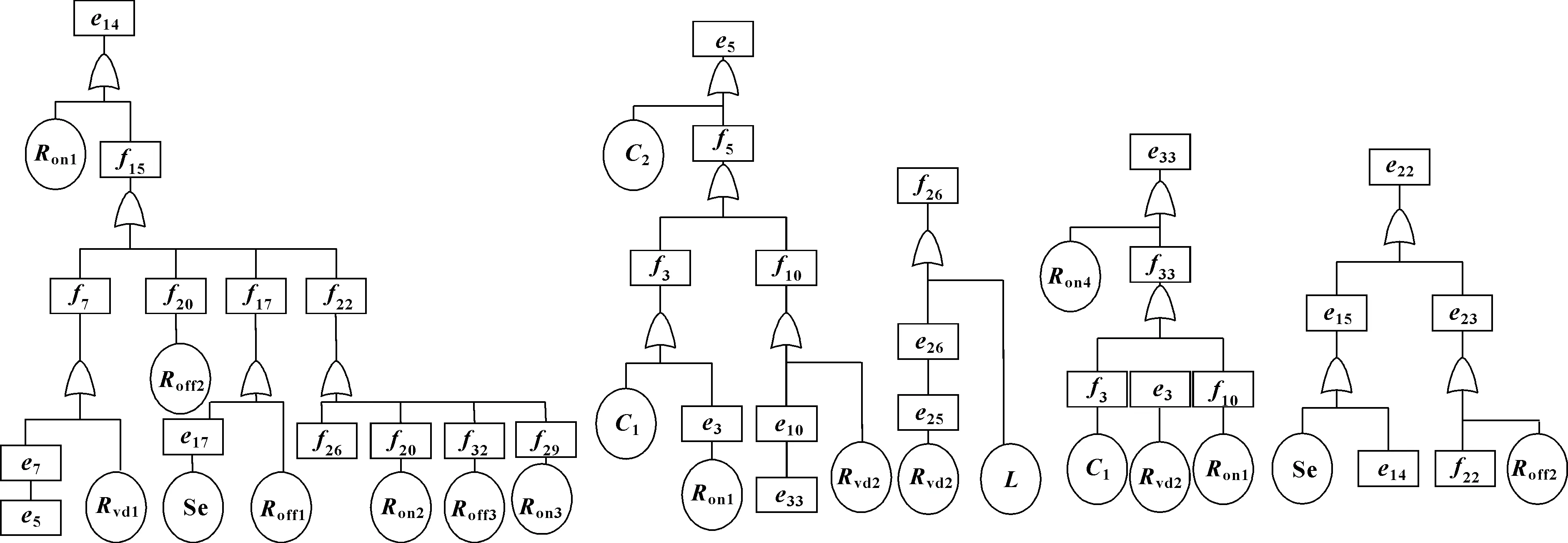
图5 故障树模型

系统的故障树模型是引起系统故障元件集合的一种定性表示，而将系统的故障树模型转化为贝叶斯网络模型后，可以将定性的故障诊断转化为定量的概率计算。将各节点的故障率代入模型，可以快速地计算任一节点的故障概率，即对系统的影响程度。故障树模型转化为贝叶斯网络模型时，其中的逻辑或门可以根据故障树与贝叶斯网络的转化规则进行转化并且给出条件概率，如图6和表3所示。转化后的贝叶斯网络模型如图7所示。

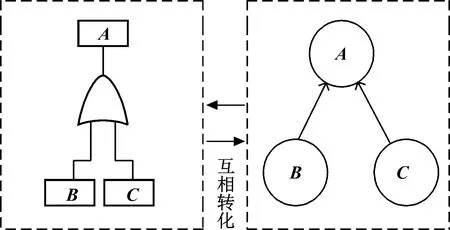
图6 逻辑或门与贝叶斯网络的转化

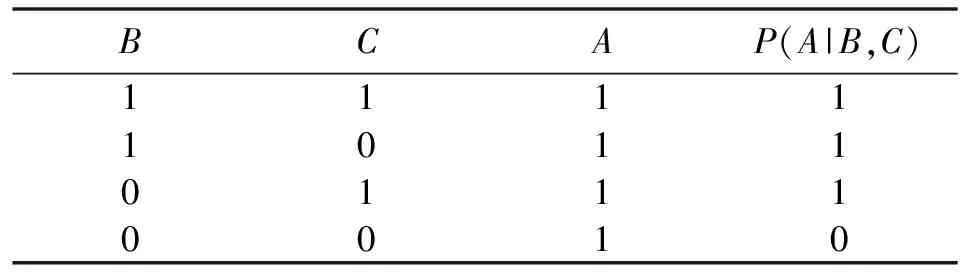
表3 逻辑或门关系的CPD

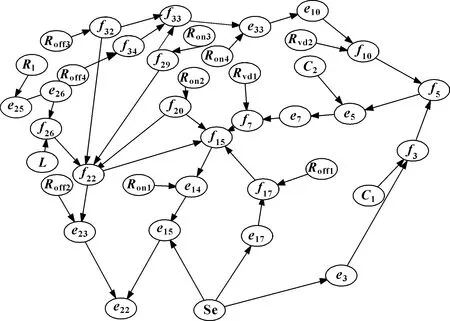
图7 系统的贝叶斯网络模型

根据RENOOIJ提出的概率表，得到各个节点的CPD如表4—表6所示。

表4 e7的CPD

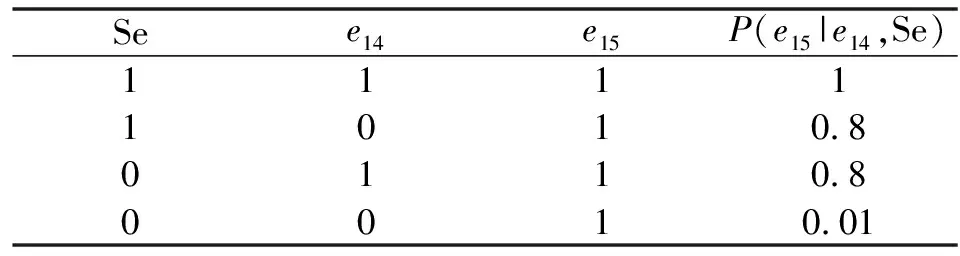
表5 e15的CPD

表6 f33的CPD

3 NPC逆变器的故障诊断与仿真结果

本文作者基于GenIe2.3软件平台，实现NPC逆变器的故障诊断仿真。在GenIe2.3软件平台中，搭建NPC逆变器的贝叶斯网络，在没有任何观测证据前，各个节点的先验概率均设为0.5。当观测到某个节点证据时，各节点的后验概率会发生变化。

当观测到节点证据时，各个根节点的后验概率值会更新，疑似故障元件的概率值会增加。以节点单故障(桥臂中点电压)为例，诊断结果如图8所示。可知：、Se、等节点的后验概率均增大，其他节点的后验概率几乎维持在设定的先验概率值0.5附近，因此这些节点与节点故障有一定联系。尤其是节点，概率增加最大，所以得出节点故障可能性较大，可以优先检查该节点。若该节点元件出现故障可以予以更换元件，若该节点无故障，按照故障概率大小，逐个进行故障排除。

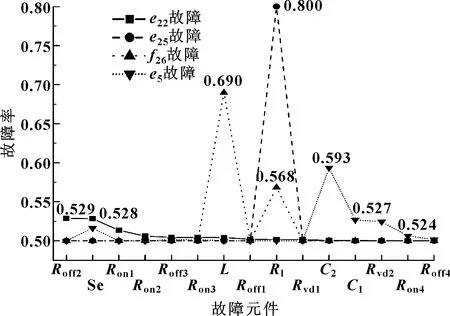
图8 单故障诊断结果

对节点进行灵敏度分析，结果如表7所示。

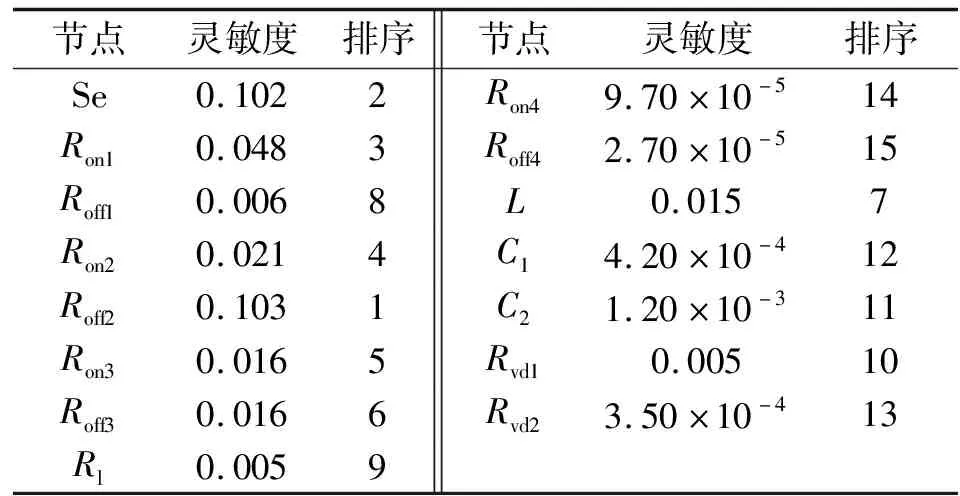
表7 节点e22灵敏度分析结果

由表7可知：节点、Se、是对节点灵敏度影响比较大的3个节点，即这3个节点的微小变动都会对节点有比较大的影响，这与通过后验概率变化得到的诊断结果一致。

该模型不仅可以诊断单故障，还可以诊断双重故障和多重故障，即观测到多个节点异常时，更新根节点的后验概率,诊断结果分别如图9和图10所示。

图9 双重故障诊断结果

图10 多重故障诊断结果

由图9可以看出：、故障时，节点、Se、、概率较其他节点明显增大，特别是节点，其概率从原来的先验概率0.5跃升为0.8。该节点的概率变化最大，说明该故障很可能主要由故障引起。因此系统检修人员应当先检查节点处元件，然后再根据故障元件的概率优先级排序来排除系统的故障。对于多重故障情况，与上述两种故障分析过程类似。根据故障元件的动态排序，可以快速定位故障元件，节省大量时间，从而为故障检修人员提供一种故障元件的维护计划。

4 结束语

由于NPC逆变器系统的元件较多，系统比较复杂，在建模时不确定程度高，出现故障时往往很难快速定位故障元件，因此，本文作者提出一种基于键合图和贝叶斯网络的故障诊断方法，结合了键合图对于复杂系统的建模优势和贝叶斯网络对不确定知识的表达、推理优势，实现对复杂系统的故障诊断。该诊断方法直观地反映了故障元件和故障节点的关系，不仅可以定位到故障元件，还可以计算出故障元件对系统的影响程度。结果表明：该方法不仅可以诊断单个元件故障，还可以诊断系统的复合故障。

贝叶斯网络灵活性强，适用于复杂系统的故障诊断研究，随着系统元件的使用，可不断对元件概率进行修正，模型的准确度会越来越高。