基于指数增益迭代学习算法的机械臂轨迹跟踪
2022-09-15郑铭跃张方蒋祺蒙奎全朱伟
郑铭跃,张方,蒋祺,蒙奎全,朱伟
(1.南京航空航天大学机械结构力学及控制国家重点实验室,江苏南京 210016;2.昆山华恒焊接股份有限公司,江苏昆山 215300)
0 前言
机械臂的轨迹跟踪问题指的是通过给定机械臂一条期望的工作轨迹,在确定好机械臂的各个参数并设定好控制器的参数之后,使得机械臂能按给定的期望轨迹工作。然而现实中的机械臂却是一个具有不确定性、强耦合和非线性等特点的复杂系统,而在机械臂建模过程中同样有许多不确定因素,且工业机械臂的制造过程中同样存在制造误差,因此难以建立准确的机械臂动力学模型。而机械臂的控制品质依赖于机械臂模型的准确性,所以国内外学者不断寻求新的理论及控制方法以提高机械臂的控制精度。目前应用于机械臂轨迹跟踪的控制方法有传统的比例积分微分控制算法(PID)、计算力矩法,以及较为先进的模糊控制算法、自适应控制、滑模控制算法等。针对工业中机械臂在工作中经常重复运行,发展出了迭代学习控制ILC(Iterative Learning Control)。
迭代学习算法最早是在1978年由日本学者UCHIYAMA创立,并于1984年被ARIMOTO正式提出。ARIMOT根据线性时变连续系统设计了微分(D)型迭代学习策略,并基于此策略演化出了比例(P)型、比例积分(PI)型、比例积分微分(PID)型迭代学习策略。目前,BOUAKRIF提出了一种具有初始态算法的微分(D)型迭代学习算法,避免了每次迭代时需要选择初始状态值;郭文雅对迭代学习算法中的收敛速度进行研究,让算法的收敛速度加快。通过可调节区间证明Lebesgue-p范数下的加速迭代学习控制,兰天一和林辉基于比例微分(PD)控制算法,提出了变增益加速迭代学习控制算法,并证明了该算法的收敛性。H B WANG、Y WANG将相邻迭代次数同一时刻的迭代误差添加到了传统的比例(P)迭代学习中,提出了新型快速迭代学习算法,改善了机械臂迭代学习过程中的初态偏移问题,缺点是收敛速度较慢。何熊熊等将自适应控制与迭代学习控制结合在一起,提高了该算法的鲁棒性。
本文作者为提高某焊接机械臂的轨迹跟踪精度,基于传统比例微分(PD)迭代学习控制算法,提出一种指数变增益迭代学习算法,并验证了该算法的收敛性。利用ADAMS对机械臂进行参数辨识得到机械臂的惯性参数。针对机械臂的前3个控制空间坐标的关节,建立了动力学模型,利用MATLAB中的Simulink功能,以及函数的使用,对这3个关节进行轨迹跟踪仿真,并与传统的迭代学习控制进行了比较。
1 机器臂模型
表1为该焊接机器人的DH参数,将SolidWorks中机器人的3D模型导入到ADAMS中,模型如图1所示。
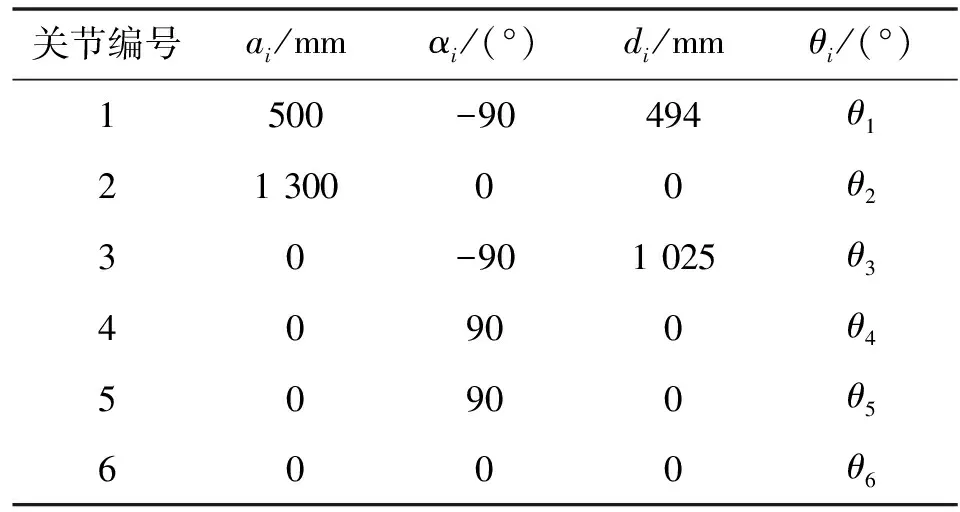
表1 机器人DH参数

图1 机器人ADAMS模型
其中:为机械臂的杆件长度;为机械臂的杆件扭角;为机械臂关节距离。通过ADAMS软件,让机器人在最优轨迹下运行,对机器人进行参数辨识,得到机器人模型的惯性参数,再利用所得到的惯性参数,进行机器人动力学模型的建模。
2 动力学分析
文中利用第二类拉格朗日法(Lagrange)对机器人进行动力学建模,并令控制器输出力矩以对机器人各个关节实现轨迹跟踪。其中Lagrange方程的表达式为
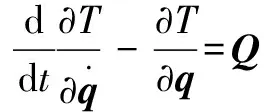
(1)
式中:为系统的动能;为广义力;为广义坐标。由Lagrange函数定义可得:
=-
(2)
其中:为系统的势能。由于势能仅与位置有关,是关于的函数,因此势能对关节速度的导数为0,因此有:
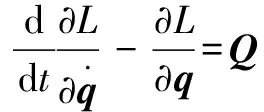
(3)
对于串联机器人,式子中的广义坐标对应于机器人关节角度,而广义力对应为作用于关节的力,该焊接机器人各关节均为转动关节,因此广义力为关节力矩。机器人杆上任意一点上的动能为
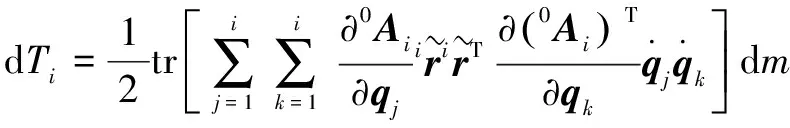
(4)
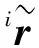
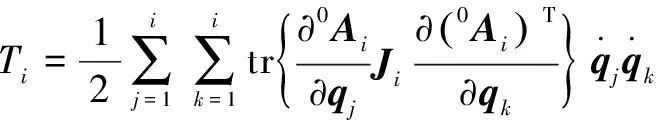
(5)
式中:用来刻画杆的质量分布情况,它包含了杆的质心以及质心对3个轴的转动惯量和惯性积,这些都可由ADAMS求得。由杆的动能可进一步求得整个机器人的动能:
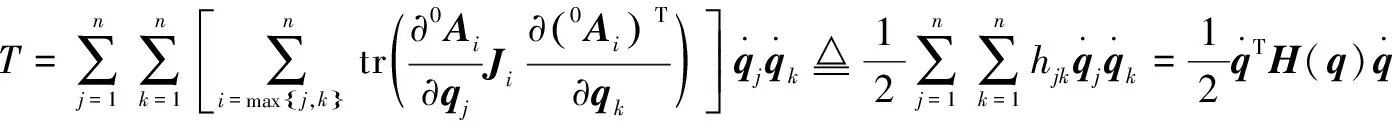
(6)
其中:()为×的矩阵,称为机器人惯性矩阵,是一个正定矩阵。杆的势能为
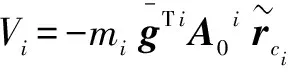
(7)
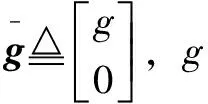
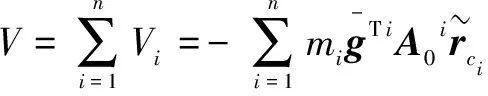
(8)
将式(6)和式(8)代入拉格朗日方程,得到:
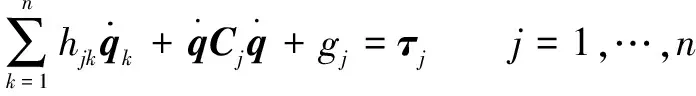
(9)
写成简洁的矩阵形式为
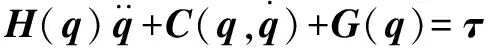
(10)
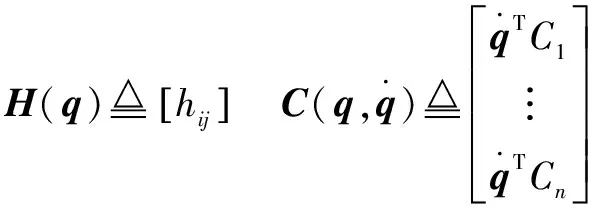
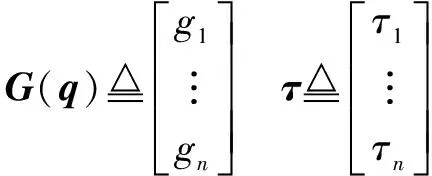
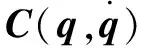
该机械臂动力学模型满足如下性质:
性质1:()是一个有界的正定矩阵,且满足
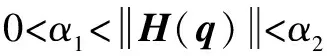
(11)
性质2:()、()满足全局Lipschitz连续条件:
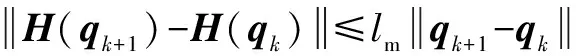
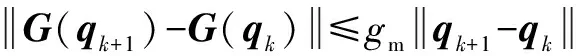
(12)
其中:是正数。
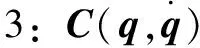
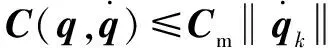
(13)
对于连续变量有引理:
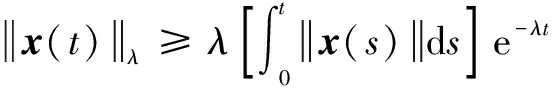
(14)
其中:为实数。
对机械臂模型作出如下假设:
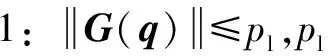
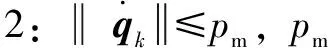
3 指数增益迭代学习控制算法及收敛性证明
对于考虑重力项的该焊接机器人,文中设计了一种指数变增益的迭代控制率,控制率为
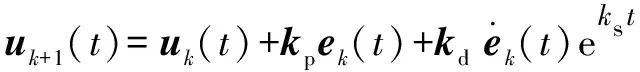
(15)
其中:=-,为第次迭代轨迹跟踪误差;、分别为系统的比例增益矩阵与微分增益矩阵;为增益修正因子。
设置状态变量:
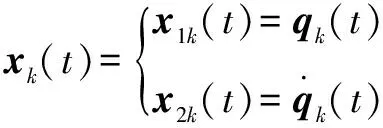
(16)
于是可得状态方程:
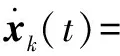
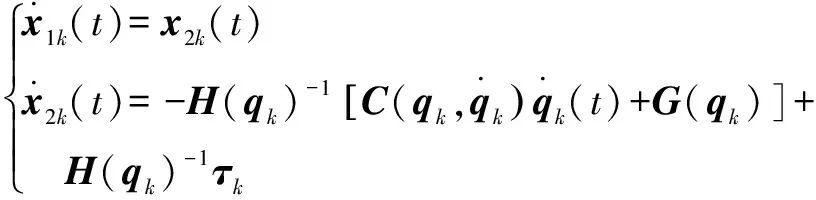
(17)
式(17)可简化为
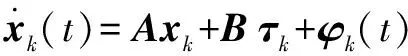
(18)
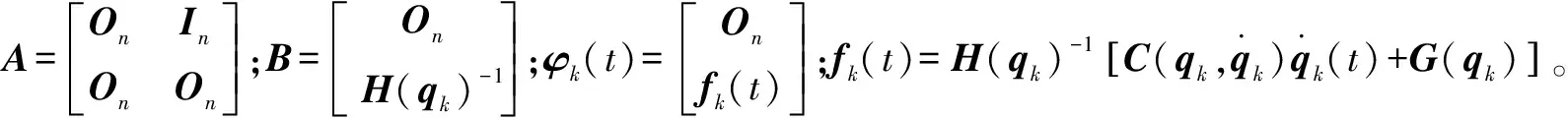
对式(18)进行求解,代入控制率[式(15)]可得:
+1()-()=()e-+


(19)
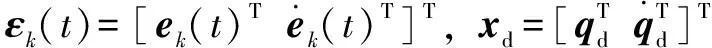
+1()-()=-()e--


(20)
整理式(20)并取范数得:
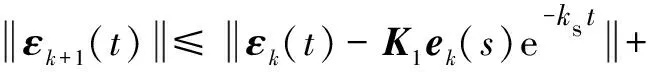
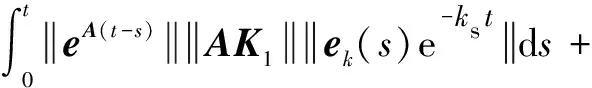
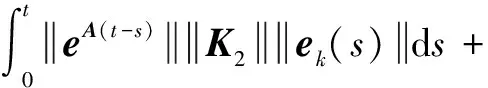
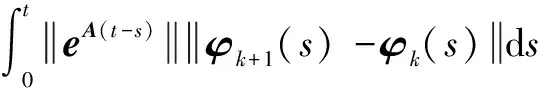
(21)
其中:
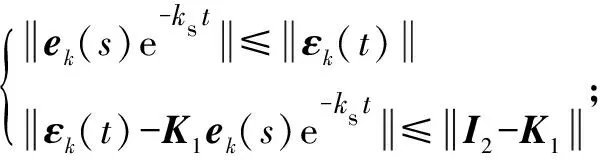
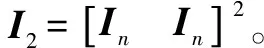
由式(18)可以得到:
+1()-()=-[(+1)-()]()-
(+1)[(+1)-()]-[(+1)-
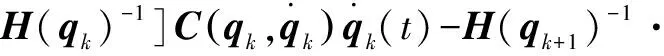

(22)
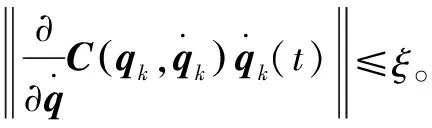
由式(22)以及性质1—3和机械臂系统的假设,可以得到:
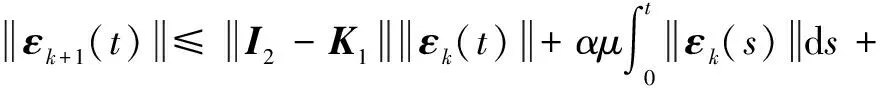
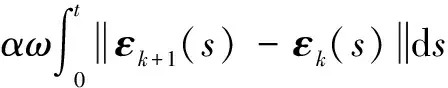
(23)
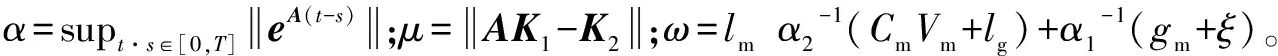
在式(23)两边同时乘以e-,可得:

(24)
由式(24)可得,当足够大时有:
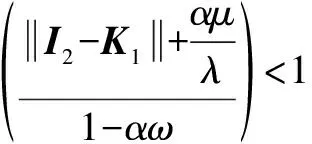
(25)
于是可以得到:
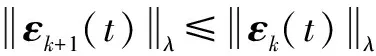
(26)
从而有:
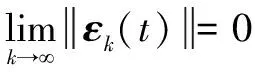
(27)
即:
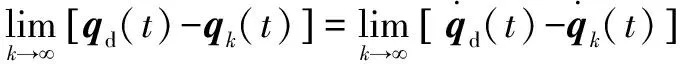
(28)
因此该控制算法在迭代次数足够多时,可以追踪到期望轨迹。
4 仿真实验与实验结果分析
文中通过MATLAB来验证控制算法的有效性,使用MATLAB中的Simulink以及S函数模块来完成对该焊接机器人的轨迹跟踪仿真。MATLAB代码于MATLAB R2017a的环境下运行。机器人模型简图如图2所示。由于机器人后3个关节主要控制机器人末端的姿态,因此仿真时只对机器人的前3个关节进行讨论,将后3个关节的质量与第3个关节结合在一起,将它们看作一个整体。机器人的动力学模型见式(10)。

图2 机械臂DH简图
仿真时机械臂参数由ADAMS参数辨识得到。其中关节1质量=778.945 kg,关节2质量=656.701 kg,关节3质量=483.232 kg。
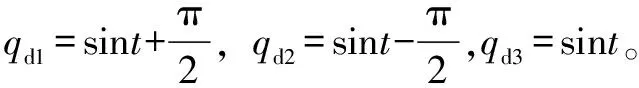
4.1 传统迭代学习仿真
传统迭代学习控制的学习率为
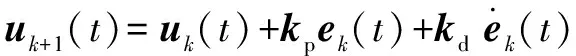
(29)
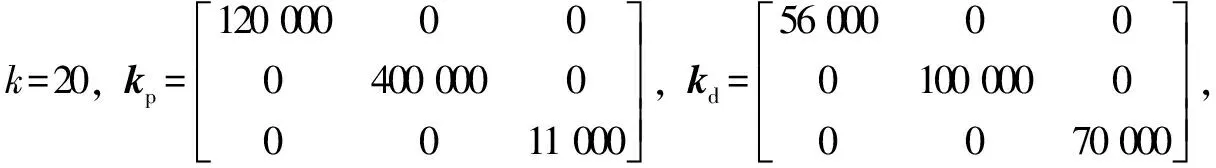
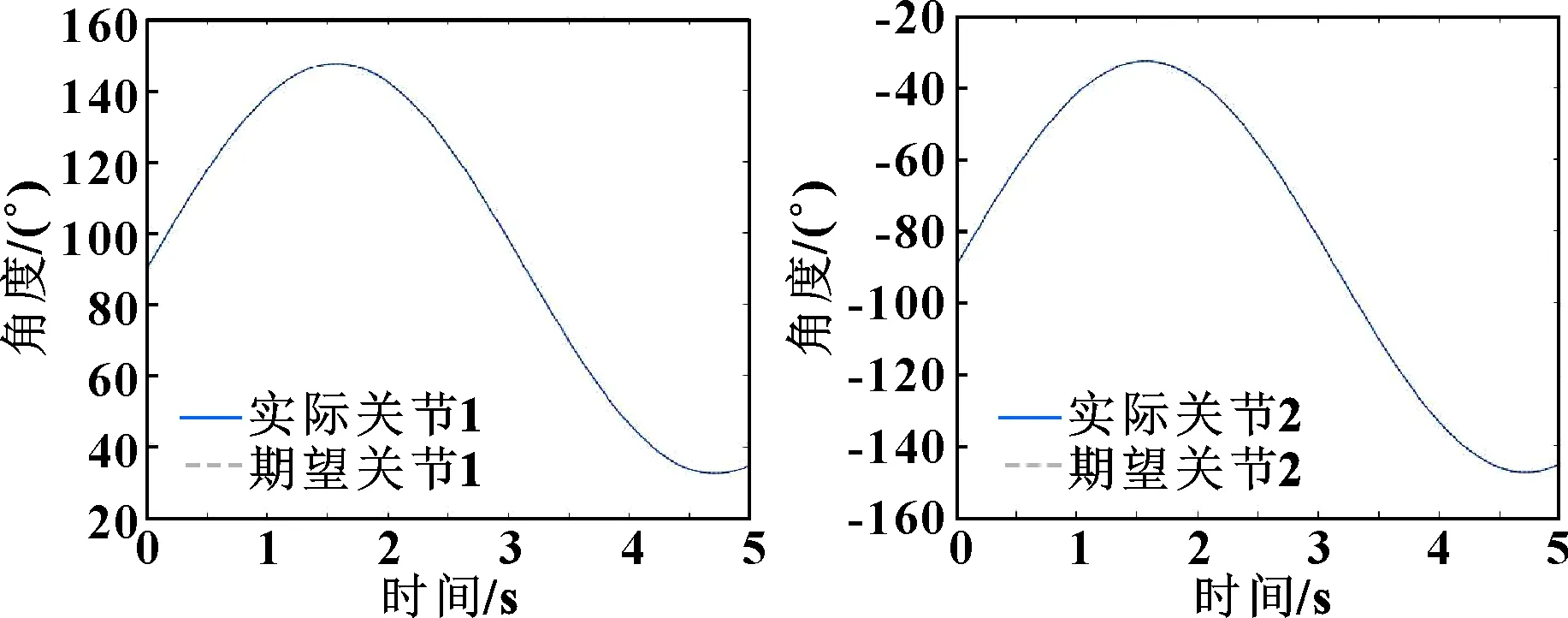
图3 关节1实际轨迹与期望轨迹(传统算法) 图4 关节2实际轨迹与期望轨迹(传统算法)
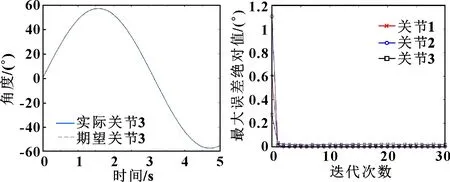
图5 关节3实际轨迹与期望轨迹(传统算法) 图6 各关节随迭代次数误差变化(传统算法)
从图3—图5中可以看出:传统迭代学习算法经过30次迭代后能够完全地追踪期望轨迹。而从图6可以看出:经过第一次控制算法控制后,3个关节的误差已经缩小到1°左右,前3次迭代误差减小速度较快,而经过第4次迭代之后,3个关节的误差已经基本为0°,实际轨迹已经完全追踪到期望轨迹。
4.2 指数增益迭代学习仿真
为了更好地对比指数增益迭代学习算法与传统迭代学习算法,将比例增益系数和微分增益系数设置得和传统迭代学习相同,而修正系数取0.1,图7—图9为机械臂3个关节在迭代30次后的实时轨迹与期望轨迹的对比图。图10为机械臂3个关节轨迹跟踪误差随着迭代次数的变化。
从图7—图9中可以看出:指数增益迭代学习算法经过30次迭代后能够完全地追踪期望轨迹,证明了指数增益迭代学习控制算法的收敛性。通过图10可以看出:在前2次迭代过程中,指数增益迭代学习算法收敛速度很快,并在第3次将误差减小到0的邻域内,之后的误差稳定在0邻域附近。相比于传统的迭代学习算法,指数增益迭代学习算法收敛更快,且第3关节的误差在迭代过程中逐渐缩小,没有出现浮动,充分说明文中提出的指数变增益迭代学习算法的效果。

图7 关节1实际轨迹与期望轨迹(文中算法) 图8 关节2实际轨迹与期望轨迹(文中算法)
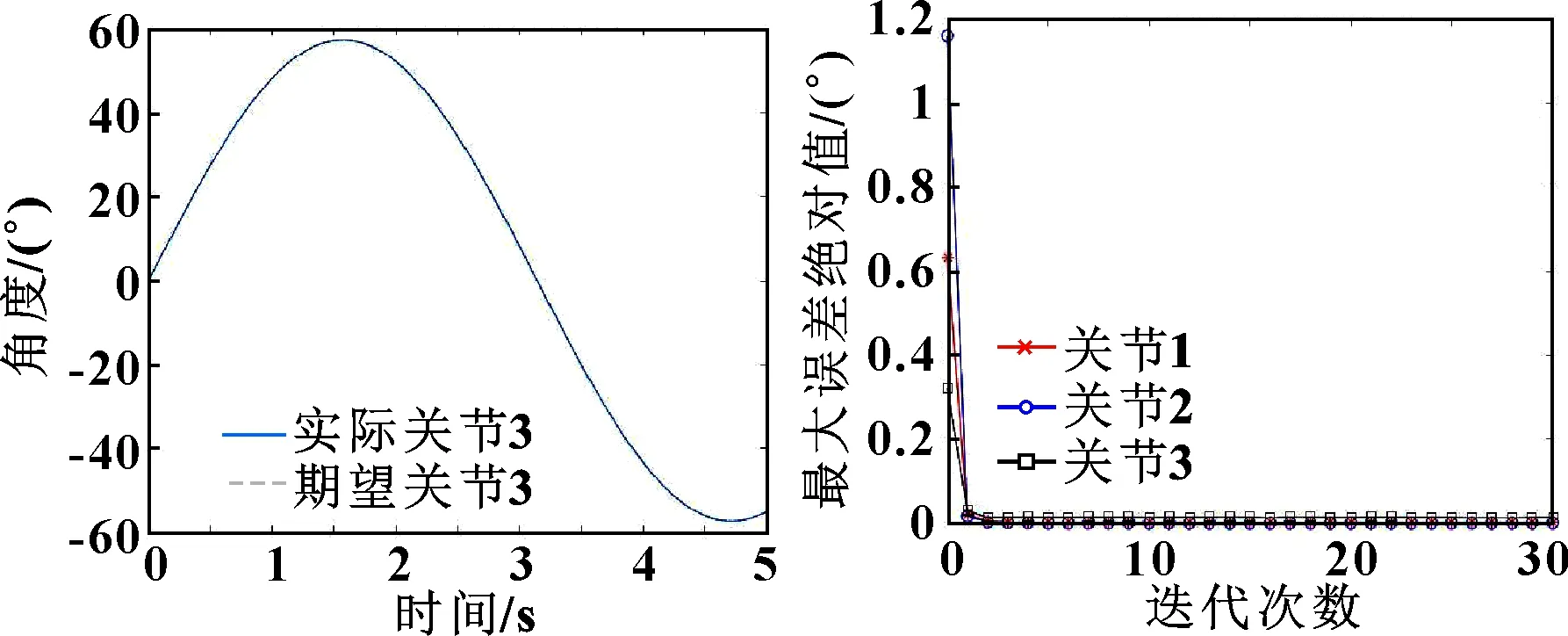
图9 关节3实际轨迹与期望轨迹(文中算法) 图10 各关节随迭代次数误差变化(文中算法)
5 结论
文中针对某六自由度焊接机器人,建立了简易的动力学模型,并针对其前3个关节提出了一种指数变增益迭代学习控制算法,通过在控制率的微分增益上添加修正系数来达到加快控制算法收敛的效果。利用MATLAB进行仿真,将提出的指数变增益迭代学习控制算法与传统的迭代学习算法进行了比较,证明了提出的算法收敛更快。缺点是三关节机械臂的计算量较大,且迭代次数的增加也会增大计算量,计算机需要花费更多的时间去计算。今后的研究可以着重放在加快该算法的运算速度等问题上。
