基于OBE理念的问题驱动教学改革与实践——以数据结构进阶课程为例

柳 欣 李保田 薛玉利 唐 艳

1.山东青年政治学院信息工程学院，山东 济南 250103

2.山东省高校信息安全与智能控制重点实验室（山东青年政治学院），山东 济南 250103

数据结构进阶课程是我校计算机科学与技术专业的专业选修课。该课程对先修课程数据结构和算法设计与分析的教学内容进行了补充，同时对这两门课程的重点内容进行了知识归纳和算法设计的思维拓展，形成了完整的数据结构与算法知识链。通过本课程的学习，学生能深入理解典型数据结构的重要性质、存储结构以及具体实现，掌握重点算法，并能运用数据结构技术和算法设计策略分析、解决现实应用中的问题，培养软件开发素质、工程意识和职业道德规范。数据结构进阶课程的教学内容中包含大量复杂算法，这些算法具有存储结构定义复杂、算法执行过程抽象、实验难度大等特点，在传统教学模式下，教师往往会面临“教师讲不动、学生没兴趣”的双重困境。

一、支撑的教学理论

问题驱动教学是一种“以学生为主体、以问题为核心”的教学方法，其特点如下：（1）教师将教学内容嵌入精心创设的问题情境中，将课堂教学转换为不断地提出问题和解决问题的迭代过程。（2）强调学生是学习主体，是知识的主动探究者。教师的角色是组织和引导对问题的讨论，并且为学生提供必要的帮助。（3）教学目标不是靠教师讲授直接达成的，而是在教师与学生的共同努力下以递进方式达成的，具体表现为认识问题，探索解决关键问题的途径，逐步求精地解决问题，对不同的问题解决方法进行比较以及通过思考发散性问题实现知识拓展。成果导向教育（OBE,Outcomes-based Edu‐cation）是工程教育专业认证的核心理念，它强调首先明确学生的学习成果（即毕业要求），然后根据毕业要求对课程的教学目标和教学内容进行反向设计。思维可视化是一种利用图像、媒介、言语和肢体表征对不可见的思维进行直观展示的技术。该技术的成功运用可以加强学生的思维训练，提升他们的创新思维层次。

二、问题驱动教学改革总体思路

（一）OBE理念下的教学目标制订

根据工程教育认证标准，我们将人才培养方案中的毕业要求细化为33 个二级指标点。数据结构进阶课程对其中的4 个指标点形成支撑（如表1 所示），分别侧重对学生的应用能力、分析能力、设计能力和职业规范进行培养。

在确定这些指标点之后，我们设置了4 个与之相应的教学目标（如表2所示）。

（二）案例算法选取

在教学目标确定之后，我们遴选了一部分有代表性的复杂算法作为实施问题驱动教学的内容。具体遴选原则如下：1.算法的底层存储结构具有代表性，学习该算法有助于学生加深对顺序/链式存储结构的理解。2.算法的设计思想体现了典型的算法设计策略，能较好地对数据结构进阶课程和先修课程算法设计与分析的教学内容进行衔接。3.算法有着较为广泛的现实应用，有利于与思政元素进行结合。

（三）教学难点分析以及应对策略

在选定教学内容之后，我们结合教材中的算法描述，对有可能给学生理解造成障碍的关键点进行分析。以模式匹配算法为例，教材中介绍了两个算法，即BF（Brute Force）的模式匹配算法和KMP（Kruth-Morris-Pratt）模式匹配算法。这两个算法都采用了顺序存储结构，其核心思想是借助游标i 和j 对主串S 和模式T 中参与匹配的当前字符进行比较。通过分析发现，在教学过程中存在以下的难点：（1）当发生“失配”时，如何对游标i进行回溯。（2）在BF模式匹配算法中，利用语句“i=i-j+2;”实现对游标i的回溯，但是这条语句的可读性欠佳。（3）教材的KMP算法描述中对“S[i]=T[j]”和“j=0”两种情况下的游标设置进行了合并，致使理解算法的难度增大。

针对教学难点，我们采取了以下的应对策略：（1）在许多复杂算法中，都是先对特定条件做出判断，然后分情况进行处理。对这些情况进行图解，可以为学生自主探究提供最有效的学习“支架”。（2）教材中的算法描述往往是最精简的形式，缺点是容易造成阅读和理解的困难。对此，可以采用问题驱动教学方法，先引导学生将精力放在如何解决问题上，在归纳得出算法描述之后，再对算法描述进行化简，最终得出与教材相同的算法描述。

（四）OBE 理念指导下的问题设计与问题驱动教学详细设计

针对教学难点，我们在OBE理念指导下进行问题设计。教师将在问题驱动教学过程的不同阶段提出这些问题，既能实现问题的抽丝剥茧、逐步求精，又能对人才培养方案中有关能力培养和职业规范的指标点进行支撑。以模式匹配算法为例，我们针对教学内容设置了10个具体问题（如表3所示）。

在完成问题设计之后，需要围绕这些问题开展问题驱动教学的详细设计。在该过程中，我们采用文献［3］的做法，将每个阶段的教学过程划分为多个循序渐进的板块，即问题情境、自主探究、合作交流、总结提升和迁移拓展。

三、问题驱动教学设计举例

我们以模式匹配算法为例，给出一个具体的问题驱动教学的教学设计案例（教师提出的问题均来自表3）。本次课的教学目标如下：（1）理解字符串的顺序存储结构、掌握BF 模式匹配算法和KMP 模式匹配算法。（2）通过课程思政使学生了解社会主义核心价值观倡导的诚信理念，保持科研诚信、杜绝抄袭行为。考虑到KMP 算法是在BF 算法基础上改进得到的，我们将整个教学过程分为以下两个阶段。

（一）第一阶段——朴素模式匹配算法的问题驱动教学

问题情境板块：教师介绍教材中的病毒感染检测案例，并且提出问题1。

自主探究板块：首先，教师简要回顾字符串顺序存储结构，并且提出问题2。接下来，教师提供对模式匹配问题的完整描述以及重要的符号定义。最后，教师向学生提供有关算法匹配过程中“成功”和“失配”两种情况下的图示（如图1所示，匹配成功的区域用灰色填充），并且提出问题3。该板块结束后，学生会在教师提示下自行写出算法描述。

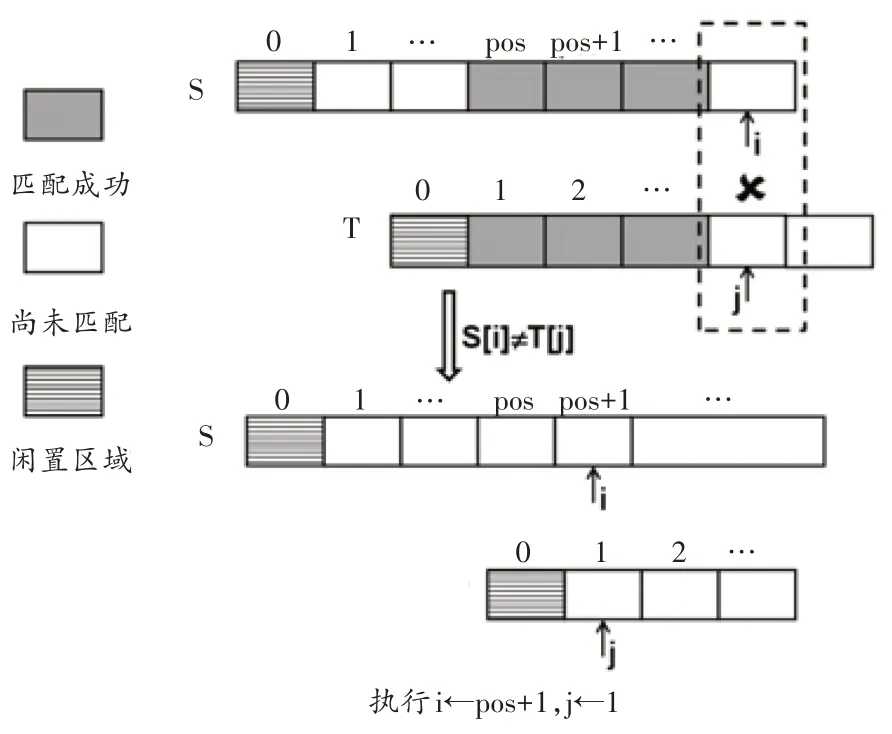
合作交流板块：教师要求学生以小组为单位将写出的算法描述与教材中的算法描述进行对照。容易发现，两者并不一致。这主要体现在，当发生失配时，教材并未使用语句“i=pos+1;”对游标i进行回溯，而是使用了令人费解的语句“i=i-j+2;”。对此，教师提出问题4，并且为学生提供一个具体的例子作为学习支架（见图2）。通过讨论，学生终于理解如果将回溯位置pos+1 视为未知数，同时将i 和j 的当前位置视为已知数，则可以通过解方程而求出pos+1的值，即i-j+2。

总结提升板块：为了巩固学习成果，教师向学生提供文献［8］中的模式匹配问题实例S="ababcabcacbab"，T="abcac"，并且要求学生利用图解方法进行模式匹配，且主串S的匹配开始位置为i=3。这是一个精心设计的“陷阱”，学生需要总共执行4 轮模式匹配（即当主串的匹配起始位置为i=6时）才能最终取得匹配成功。此时，学生发觉算法的回溯策略并非总是有效的，存在即使执行回溯也会“做无用功”的现象。此时，教师可以提出问题5。

（二）第二阶段——KMP 模式匹配算法的问题驱动教学

问题情境板块：教师介绍KMP 算法，并且指出该算法可以有效地避免上述“做无用功”的现象。同时，强调该算法假设存在一个“神奇”的next表格。

自主探究板块：教师将KMP算法每轮的匹配过程分为“本轮匹配成功”“本轮发生失配”和“上一轮发生失配导致j 回退到0”三种情况，并且利用思维可视化技术为学生提供图形化的学习支架，如图3所示，匹配成功的区域用灰色填充。最后，教师提出问题6。

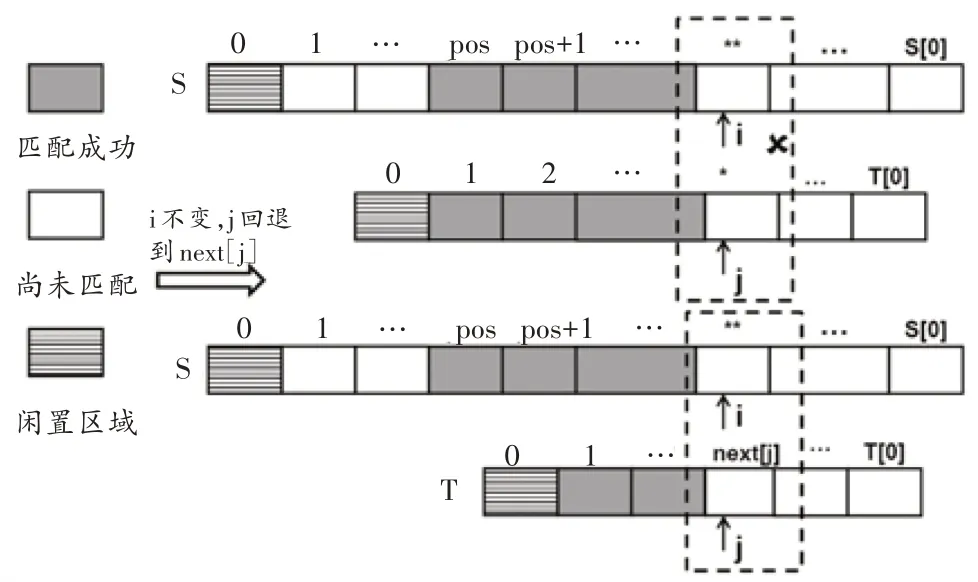
合作交流板块：教师强调，尽管已经理解了KMP 算法的核心技术，但是必须将next 表格构造出来，否则KMP算法就是“无源之水，无本之木”。在具体教学过程中，教师首先介绍用于构造next表格的手工算法，然后提出问题7。

总结提升板块：在该板块，教师提出问题8，并且以讨论的形式对两个算法进行优缺点比较。教师负责引导讨论的走向，最终得出以下结论：（1）KMP算法适合于从外存中读取主串的情况。（2）KMP 算法并非总是优于BF算法。

迁移拓展板块：教师强调学习数据结构最大的困难在于理解和设计算法。选取适当的例子进行图解分析，不但可以降低问题难度，而且有助于归纳得出算法描述中的关键语句。此时，教师提出问题9，鼓励学生将图解作为攻克复杂算法的“利器”。事实上，模式匹配算法是设计论文抄袭检测算法的重要基础。我们认为，这个思政元素与教学内容紧密结合，容易为学生所接受。因此，教师可以不失时机地介绍这个应用，并且提出问题10，使学生明确恪守职业道德、坚守学术诚信与社会主义核心价值观倡导的诚信理念在本质上是一致的。

四、满意度调查

为了了解问题驱动教学改革的实际效果，我们在结课后利用“问卷星”向学生发布了匿名调查问卷。问卷内容主要涉及课程教学满意度、问题驱动教学法对学习积极性的促进作用、对问题的难度评价、图解是否有助于对算法关键执行过程的理解、是否希望教师提供有针对性的图解作为学习支架等内容。

结果显示，有68.64%的学生认为问题驱动教学有助于提高学习积极性，有85.59%的学生赞同教师提供图解作为学习支架的做法。这说明该尝试取得了较好的效果。

五、结束语

为了改善数据结构进阶课程的教学效果，本文提出了基于OBE 理念的问题驱动教学改革思路。通过引入OBE 理念，使得课程教学目标聚焦于对学生的应用能力、分析能力、设计能力和职业规范的培养。同时，教师必须在问题设计阶段充分考虑教学内容对指标点的有效支撑。此外，以模式匹配算法为例，提出详细的问题驱动教学设计案例。今后，我们将在以下方面继续深化现有研究：（1）建立面向数据结构进阶课程的问题驱动教学案例库。（2）在OBE理念指导下，开展针对问题驱动教学内容的知识点考核达成度评价，根据评价结果改善教学方法和内容，形成“问题驱动教学—达成度评价—改进教学”的完整闭环结构。