高阶非线性Sasa-Satsuma方程的新精确单行波解分类
2022-09-14韩天勇
韩天勇,李 钊
(1.成都大学 计算机学院,四川 成都 610106;2.成都理工大学 数学地质四川省重点实验室,四川 成都 610059)
1 引言
非线性偏微分方程常用于描述很多自然现象中的演化过程[1-6].非线性Schrödinger方程是一种描述发生在多种物理情况下的非线性偏微分方程,在数学、金融、生物、化学、等离子体、非线性光学、流体力学、凝聚态物质、核物理等领域有着广泛的应用.另外,在皮秒范围内单模或单芯光纤中光孤子的传播模型也可以使用非线性Schrödinger方程描述[1-2,5].大量的实验证明光纤中存在孤立波,因而光纤中的孤立波问题受到大量学者的关注.孤立波理论在许多非线性模型中是必不可少的,尤其是光纤和其他应用物理学科,可用于光纤数字信息传输研究.这些非线性偏微分方程的精确解[7-10]在非线性现象研究中是很重要的,尤其是寻找非线性偏微分方程精确行波解的分类是最重要的研究课题之一.
本文考虑如下的(3+1)维非线性Sasa-Satsuma (SS)方程[11-12]:
(1.1)

2 精确解
考虑如下行波变换
Ψ(x,y,z,t)=Φ(ξ)eiη,
(2.1)
其中ξ=c1x+c2y+c3z+c4t,η=d1x+d2y+d3z+d4t.
将方程 (2.1)代入 (1.1),分离其实部和虚部,则(3+1)维SS 方程约化为
b3Φ3+b1Φ+b5Φ''=0,
(2.2)
(b2Φ2+b4)Φ'+b6Φ'''=0,
(2.3)
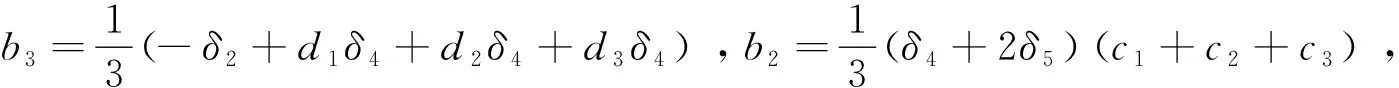
对方程(2.3)关于ξ积分一次,可得:
(2.4)
比较方程(2.2)和方程(2.4)可得
令Φ'=φ,可得系统(2.2)的如下平面动力系统:
(2.5)
方程(2.5)对应的哈密顿系统可以表示成如下形式:
利用MAPLE绘制的系统 (2.5)的相图如图1-4所示.

图1 当b2>0,e1>0时,系统(2.5)的相图
方程(2.2)两边乘Φξ后积分可得:
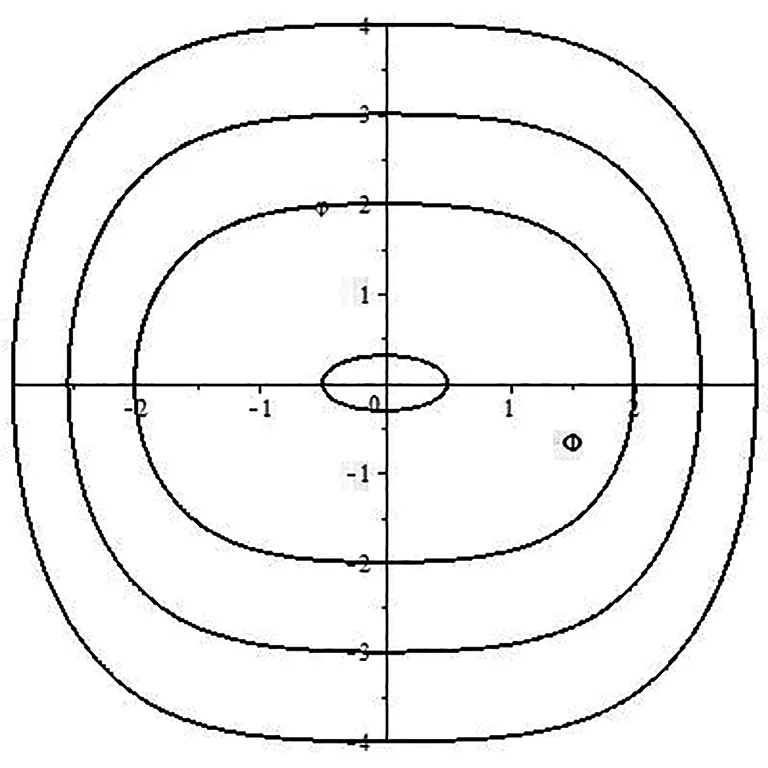
图2 当b2>0,e1<0时,系统(2.5)的相图
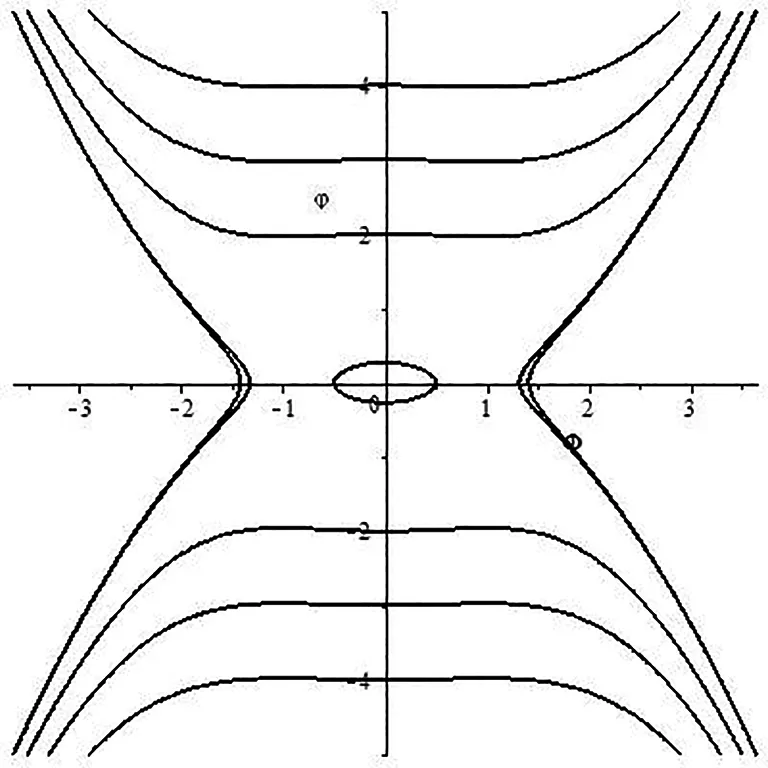
图3 当b2<0,e1<0时,系统(2.5)的相图

图4 当b2<0,e1>0时,系统(2.5)的相图
Φξ2=A4Φ4+A2Φ2+A0,
(2.6)

对方程(2.6)作如下变换:
方程(2.6)可以变形成如下形式:
(Vξ1)2=4V(V2+B1V+B0).
(2.7)
令F(V)=V2+B1V+B0,则方程(2.7)可以改写为
(2.8)
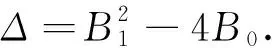
情形1.Δ=0.方程(2.8)可以改写成:
(2.9)
(1)如果B1>0,那么(2.9)的解为:
(2.10)
即
结合(2.8)、(2.10),可以得到方程(1.1)的解为
(2)如果B1<0,那么(2.6)的解为:
因此
故
ei(d1x+d2y+d3z+d4t).
ei(d1x+d2y+d3z+d4t).
(3)如果B1=0,那么(2.6)的解为:
因此,
情形2.Δ>0,B0=0 .如果V>-B1可得:
(1)如果B1>0 ,那么
因此
即
ei(d1x+d2y+d3z+d4t),
ei(d1x+d2y+d3z+d4t).
(2)如果B1<0 ,那么

ei(d1x+d2y+d3z+d4t).
情形3.Δ>0,B0≠0 ,α1<α2<α3.这里α1,α2,α3中有一个等于0,而另外两个是函数F(V) 的零点.
(1)若α1 故 因此, (2)若V>α3,考虑变量替换: 因此(1.1)有解, 因此系统(1.1)有解 , 高阶(3+1)维非线性Sasa-Satsuma方程是一类广义的Schrödinger方程在三维空间里的推广形式,它描述了光纤传输系统中超快脉冲传输中的三阶色散、自陡峭和散射效应。本文首先利用行波变换,将原方程变形成了一个非线性常微分方程,然后利用Hamilton系统,得到了方程的平面动力系统,结合图1-4给出了相图. 随后利用多项式完全判别系统给出了高阶非线性Sasa-Satsuma方程行波解新的分类.这些行波解包括了Jacobi椭圆解、三角函数和双曲函数解. 这些结果显示了光脉冲在具有自陡峭、非线性色散、散射等特征的非线性光纤中的各种传播模式.

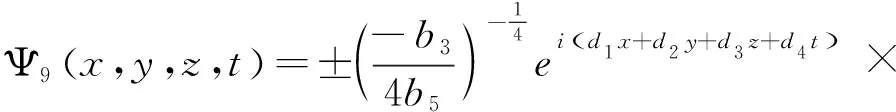


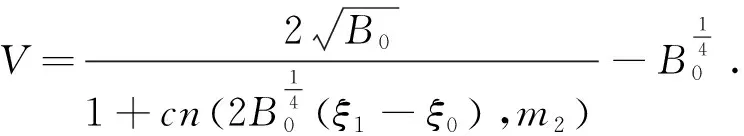

3 结论
