盖尔同心圆盘的分离

魏国祥，沈玲文

(1.四川职业技术学院 教师教育学院,四川 遂宁 629000；2.南充市高坪第五小学，四川 南充 637600)

1 引言

矩阵特征值分布是矩阵分析理论中一个极其重要的热点问题，在诸多领域有着广泛的应用[1-2].盖尔圆盘定理(Gerschgorin定理)[3]则是矩阵特征值估计中最重要的基本定理之一，许多特征值分布估计都与之有密切联系.该定理指出矩阵An×n的所有特征值包含在以对角线元素为圆心的n个圆盘的并集中.即

(1)

若某个圆盘{z||z-aii|≤Ri(A)}孤立(即与其它圆盘不相交)，则该圆盘中有且仅有一个特征值，k个圆盘构成的连通区域定含k个特征值，但不保证每个圆盘都包含一个特征值.

为得到每个特征值更准确的分布估计，许多学者对其进行了深入的研究并得到一些新的结果[4-5].其中最为常用的方法是利用可逆对角矩阵D=diag(d1,d2,…,dn)进行相似变换D-1AD，缩小部分圆盘半径，使连通的圆盘相互分离.文献[6]给出了对角相似变换能分离两个连通圆盘的一个充分条件.文献[7]纠正了文献[6]的一些问题，并对如何选择对角阵进行了一些讨论.文献[7]对正规阵给出了更小的独立圆盘半径.然而利用对角矩阵进行相似变换，仅能使各圆盘半径发生伸缩，对于同心圆盘却始终无法分离.比如考虑下例：

本文主要研究如何使同心圆盘分离，从而给出特征值更精确的分布估计，显然对角相似变化无法达到这一目的.经分析发现，一种常见的简单相似变换可将同心圆盘的两个圆心进行反向平移，使原本重叠的两个圆心分离，尽可能达到分离圆盘之目的.文中Cn×n表示所有n阶复方阵组成的集合.

2 主要方法

首先我们给出一种使两个重叠圆心分离的简单方法.

定理1 设A∈Cn×n且aii=ajj,(i≠j)为一对相等对角元，作相似变换B=PAP-1，则原重叠圆心aii=ajj,(i≠j)变换后的距离为2|paij|，其中P表示第i行的p倍(p≠0)加到第j行的初等变换矩阵，即

证明显然，P为可逆矩阵.令B=PAP-1，简单计算可知，变换后矩阵B的第i,j个对角元素分别为：bii=aii-paij和bjj=ajj+paij，|bii-bjj|=2|paij|，证毕.

下面对具体变换时的情况进行一些讨论.

(1)不难看出，若aij≠0，则变换前重叠的两个圆心aii=ajj,(i≠j)被反向平移了，对应新的两个圆盘圆心分别为bii=aii-paij和bjj=ajj+paij.但若aii=0，则上述方法失效，此时若aij≠0，则可考虑对AT进行以上变换.

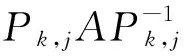
(3)两个圆心被反向平移的距离为|bii-bjj|=2|paij|，与参数p相关，取值过大容易平移太多而与其它圆盘相交，取值过小又会平移不够而影响分离效果.合理的取值对分离效果有积极作用，变换时应结合矩阵自身特点进行选取.如考虑如下矩阵

从而得到矩阵的特征值包含在如下四个圆盘的并集中：G1={z:|z-1.9|≤0.1}，G2={z:|z-2.1|≤0.2}，G3={z:|z-1|≤0.2}，G4={z:|z|≤0.3}.圆盘G1与G2圆心已经分离，但两个圆盘尚未分离.圆盘G3和G4独立，各含一个特征值.此时可考虑适当增大p的取值，如p=2，则得到

下面，我们给出使重叠圆盘分离的一个充分条件：

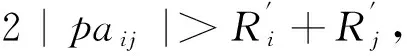
证明计算矩阵B=PAP-1的第i行和第j行的元素即得.

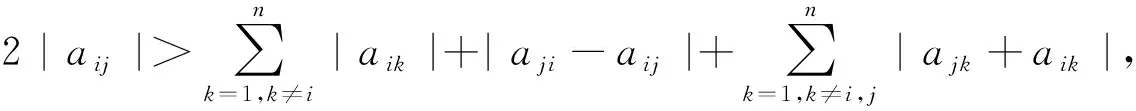
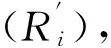
注2 如需得到更精确的分布区域，还可将多种方法得到的分布区域取交集，由此能进一步缩小特征值分布范围.

3 数值算例

最后给出几个数值算例说明上述方法的有效性.