考虑灵活性需求的园区综合能源系统协同优化配置

林顺富，曾旭文，沈运帷，李东东

（上海电力大学 电气工程学院，上海 200090）

0 引言

为了应对能源供应和气候恶化的问题，亟需构建安全高效可持续发展的能源体系。在多项政策支持与信息物理条件逐渐满足的新环境下，综合能源系统IES（Integrated Energy System）以电为中心，集成多个能源子系统，打破不同系统间的管理壁垒，着眼于提高系统整体经济性与可靠性，已成为促进能源梯级利用、提高可再生能源消纳能力的重要手段［1］。在此基础上，为满足多能耦合、多荷交叉的能源需求，对融合多级能量流与信息流的IES 规划问题进行研究十分必要。

对于区域规模较大或跨区域的IES 通常需同时优化系统配置和网架结构［2］，而对于规模较小的园区IES 或多能互补微网通常仅需优化IES 内各类设备的容量和类型，根据优化过程中设备容量的选取（离散变量或连续变量）又可分为设备选型和设备定容2 个问题［3］。文献［2］建立了能量枢纽模型，将其分为2 层，在确定备选机组容量和型号的情况下，基于图论实现上层能源传输网络和下层机组容量及型号的整体规划。文献［3］同时考虑经济性和可靠性建立多目标的IES 优化配置模型，采用序贯蒙特卡洛法对各设备状态进行模拟，实现配置方案可靠性的量化。文献［4］研究了储能接入对IES 安全边界的影响，所提配置方法可提供经济性、安全性不同的多种配置方案。然而，上述文献将终端用户的用能情况视为恒定，并未考虑灵活需求对规划的影响。需求响应技术旨在提高新型电力系统负荷调控能力，随着IES 的发展以及新能源渗透率的提高，发电侧的波动性愈加明显，对电力系统灵活调节能力提出更高要求，传统电力需求响应逐步衍生和扩展为综合需求响应IDR（Integrated Demand Response），IDR 项目中的各类负荷不仅可以通过削减、转移的方式参与其中，也可通过转换能源消耗种类的方式扩大IDR 的响应潜力［5］。文献［6］建立了电力、热力柔性负荷精细化模型，分析IDR 的引入对储能设备配置和IES 灵活性的影响。文献［7］基于价格型需求响应分析了IDR 对系统运行效益及环境效益的贡献，且在不同碳排放约束下研究了能源价格变动对IES配置结果的影响。然而，终端用户响应行为存在灵活多变、难以控制的特点，因此考虑灵活性的负荷调控将不可避免地增加IES 不确定性，需要进一步研究能准确描述用户响应不确定性的方法。目前，针对用户响应行为不确定性的表示方法包括随机概率法［8］、鲁棒优化法［9］、区间理论［10］、模糊理论［11］等。但是随机概率法和模糊理论对数据量和原始数据的准确度要求较高，在实际案例中获得精确的概率密度函数和可靠的原始数据往往较困难；鲁棒优化和区间理论将不确定变量分别限制在最恶劣情况或一定区间内，可能导致对原始数据的不确定性分析不足或求解结果相对保守的问题。上述方法均未考虑原始建模数据的可靠性程度对所建模型的影响，且现有研究中考虑IDR 不确定性因素主要集中于IES低碳经济调度问题，但是建设前期的设备配置和实际运行调度情况相互制约、相互影响，因此有必要在规划阶段进一步考虑IDR不确定性。

综上，本文提出了一种计及灵活性需求及新能源不确定性的IES 双层协同优化配置模型。供给侧基于Frank-Copula 函数充分考虑风光出力的不确定性与相关性，采用场景生成与削减的方法得到典型日风光出力曲线；需求侧基于Z-number 的方法描述IDR 响应时间和用能形式两方面的响应特性，该方法可结合用户响应行为的天然随机性以及先验数据可信度来表示不确定性信息；同时考虑电价方案对IDR响应量的影响，建立以IES运营商年化总成本最低为目标的双层规划模型，以此优化设备选型与各机组运行出力，并通过仿真算例验证模型的有效性和经济性。

1 计及IDR的IES模型

1.1 IES结构

本文以包含小型风机WT（Wind Turbine）和光伏PV（PhotoVoltaic）机组的园区IES 为例，IES 结构如图1 所示。实际应用中，IES 大多是以冷／热／电联供系统为核心［12］，因此为了更好地描述园区IES的能流耦合关系，提高能源综合利用效率及实用性，本文所构建的IES 模型包含的能源设备具体如下：热电联供CHP（Combined Heating and Power）机组、WT、PV、燃气锅炉GB（Gas Boiler）、吸收式制冷机AC（Absorption Cooler）、电制冷机EC（Electric Cooler）、电锅炉EB（Electric Boiler）、蓄电池BT（BatTery）、储冷设备ISE（Ice-thermal Storage Equipment）及储热设备HSE（Heat Storage Equipment）。

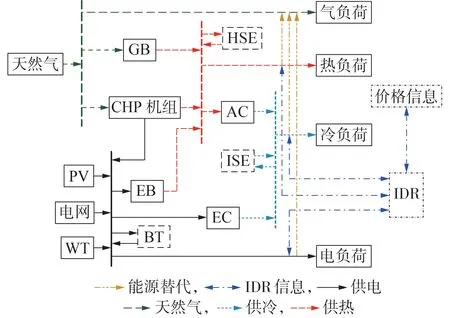
图1 计及IDR的IES结构Fig.1 Structure of IES with IDR

在供给侧，IES直接与外部配电网及天然气网络相连，对于园区内小型WT 与PV 机组，采用“自发自用、完全消纳”的运行机制，本地各类负荷需求优先由新能源满足。在需求侧，该系统中主要的终端用户分为冷、热、电、气负荷4 类：电负荷由PV、WT、CHP 机组、BT 和电网供给；热负荷由CHP 机组、GB、EB、HSE 联合供给；冷负荷需求由AC、EC、ISE 满足；气负荷则由天然气直接供应。园区内实施IDR，利用电价的变化引导需求侧调整自身用能方式与响应量，从而改变能源消耗水平并实现能源间的相互转化。

1.2 考虑IDR的负荷建模

从物理角度而言，用户的响应度主要由其负载的运行特性决定。实际上，由于用户有不同的负荷构成和用能习惯，其需求响应度差异很大。根据使用性质，IES中的用能设备可以分为基本负荷与柔性负荷。

1.2.1 基本负荷

基本负荷是指用户基本生活与生产的最低用能需求，具有较高优先级且必须即时满足。该类负荷主要包括电视、电磁炉、基本照明等，用能情况几乎不受价格信息的影响，因此不具备参与IDR 的能力。基本负荷的模型可表示为：

1.2.2 柔性负荷

本文考虑的柔性负荷主要分为3 类，分别是可削减负荷、可转移负荷、可替代负荷，这3 类柔性负荷的价格响应机理是一致的，均与柔性负荷基准值、用户价格敏感度、电价改变量有关。但是由于3 类柔性负荷响应约束不同，因此模型的具体表述形式也不尽相同。

可削减负荷是指在某个时段由于电价的改变，可以在一定范围内调整能源用量的负荷，通常包括亮度可调的照明设备、功率模式可调的采暖设备等。可削减负荷的价格响应特性可描述为：

可转移负荷是指在一个响应周期内，工作时长和工作时段皆可灵活调整，但负荷总量恒定不变的负荷。典型的可转移负荷包括洗衣机、电动汽车等，可由式（3）描述其响应特性。此外可转移负荷还需要满足转移能量守恒约束以及参与IDR 后可转移负荷的恢复与分配约束，分别如式（4）和式（5）所示。

可替代负荷是指用户能利用电能或天然气2 种能源，满足相同用能需求的负荷。不同于可削减、可转移负荷沿时间轴在不同时段间的纵向变化，可替代负荷表现为同一时段内不同能源间的横向转换［13］。由于用户的购能方式仅为电力与天然气，因此冷、热、电负荷之间的替代并非本文的研究重点，本文仅考虑冷、热、电负荷向气负荷单向转换，且由于用户侧可参与替换的冷、热负荷本应是通过电价收费的，因此，可通过式（7）简化计算可替代负荷转为气负荷的功率值。可替代负荷主要包括电／气两用的家用厨具、空调、热水器等，用户通过比较不同能源的价格信息来决定替代型负荷的运行模式，可替代负荷参与IDR后的响应特性可描述为：

2 计及IDR的IES不确定性分析

2.1 基于Z-number的IDR不确定性描述方法

由于区域内不同用户的行为偏好、用能习惯、价格敏感度、环境作用等因素存在不确定性偏差，因此柔性负荷模型中的价格-需求弹性系数ζn，t属于复杂不确定性变量，难以精确描述。为此，本文引入Z-number［15］模型对价格型IDR 不确定性进行建模。一方面，采用模糊约束刻画变量不完备的信息；另一方面，由于不完备信息也并非完全可靠，因此需加入一些额外特征来表征可靠程度，可运用自然语言进行描述。

Z-number 模型可表示为Z=(X，A，B)，其中A是对变量X的不确定性约束，即对X可能取值的限制，B被认为是可靠度，是对A不确定信息的可靠性度量，即同时结合认知结果与认知过程两方面因素来表示不确定性信息。以价格-需求弹性系数ζn，t为例，假设某个用户对价格信息不敏感，ζn，t为低，且IES 运营商根据负荷调研结果认为此用户ζn，t为低的可信度较高，此时可将ζn，t的Z-number 模型记为：Z=(ζn，t，低，较高可信)。在制定实际决策中，A和B是2 个模糊数，本文假定IES 内各用户价格敏感度A为梯形模糊数，梯形隶属度函数μA(x)的数值分布区间可用1 个四元组(a1，a2，a3，a4)表示；数据可信度参数B为三角模糊数，其隶属度函数μB(x)的数值分布区间可用1个三元组(b1，b2，b3)表示。

可以看出，相比于传统模糊模型仅用1 个隶属度函数表征不确定性变量，Z-number 增加了对所采集信息可靠性的度量，考虑了原始数据可靠性对不确定性变量建模的影响。在现阶段缺乏可靠的工程实测数据的情况下，通过建立基于Z-number 的IDR模型，在考虑用户响应行为天然随机性的基础上，兼顾决策者对于不确定信息可靠程度的主观判断，可更为有效地描述相关不确定性因素的真实作用效果。

2.2 Z-number不确定性参数的概率化转换

1）利用α截集，将Z-number 变量中B部分的模糊参数转换为清晰数α，将α以权重形式加乘到约束部分A的模糊数上，如图2（a）所示。

2）通过模糊期望近似不变定理对含权重约束的不规则模糊参数归一化，将Z-number 变量转换为标准模糊数［16］，如图2（b）所示，图中Z′为归一化后的标准模糊数。

图2 Z-number参数向标准模糊数转换的示意图Fig.2 Schematic diagram of Z-number parameter converted to standard fuzzy number

3）通过式（8）利用重心法［17］将所得的标准模糊变量转化为概率形式，得到等效概率分布，由此计算用户参与IDR后的多能负荷需求。

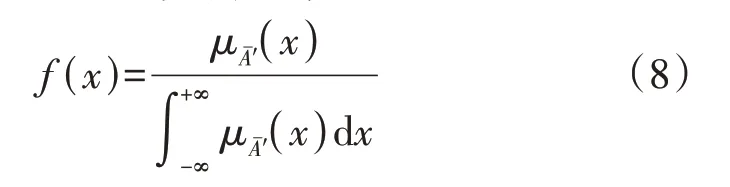
式中：μAˉ′(x)为通过步骤2）计算得到的标准模糊隶属度函数；f(x)为Z-number 参数对应的等效概率分布。

2.3 考虑风光出力相关性和不确定性的场景生成

风光出力具有不确定性和相关性，在IES 规划中，可通过具有统计特征的典型场景表征，根据前期研究成果［18］，风光出力场景生成的具体步骤如下。

3）对各时刻的风光出力联合概率分布函数进行随机采样，并通过反变换得到每个时刻WT 和PV 的采样出力。

4）为了兼顾计算的精度和速度，采用K-means方法对采样结果进行聚类，最终得到典型日场景。

3 IES双层协同优化配置

3.1 电价方案

在价格型IDR 项目中，电价水平的高低将直接影响终端用户负荷响应程度，为充分挖掘需求响应潜力，综合能源服务商只有制定合适的售电价格，才能保证IDR 的实施效果与供能经济性。本文采用文献［19］所提出的分时电价制定方法，将平均电价设为平时段电价，将峰谷时段电价上浮和下浮的比值定义为峰谷拉开比Γ，改变Γ的大小，电价方案也随之改变，进而可确定柔性负荷在不同电价方案下的用能需求，得到使IES 总成本最小的优化配置方案。为不出现峰谷倒置的情况，综合考虑用户和运营商双方利益，拉开比Γ应满足如下约束：

式中：Dv和Dp分别为谷、峰时段的用电总量。

3.2 IES双层规划模型

“双碳”目标的提出加快了能源市场的开放，在市场作用下，综合能源服务公司或园区多能源运营商多以经济利益为驱动考虑服务区域内规划问题。因此，本文以IES 运营商年化总成本最低为目标，构建上层优化不同种类能源耦合设备的型号与台数、下层优化各设备每小时出力情况的IES 双层协同配置模型。

3.2.1 上层规划模型

1）目标函数。

式中：R为所投资的固定资产残值率，取Cinve的5%；下标i指代IES 中所配置的元件种类，取1—10，与CHP 机组、GB、AC、EC、EB、WT、PV、BT、HSE、ISE 顺序一一对应；M=10；Φi为设备i的备选机组型号的集合；Cinv，ij为设备i备选型号j的单位容量安装成本；Hij为设备i备选型号j的等值年资本回收率；h为贴现率；yij为设备i备选型号j的生命周期期望值；Iij和σij分别为设备i备选型号j的安装容量和安装状态，σij为0-1 变量，σij=1 表示该设备被选中在IES 中安装，σij=0 表示该设备未被选中在IES 中安装；ε为设备维护成本系数；pc为典型日c出现的概率，下标c可指代夏季、冬季、过渡季3种典型日。

2）约束条件。

考虑到IES 运营商实际可用安装场地受限，故对所规划安装的各类能源耦合设备台数设置如下约束：

3.3 模型求解

考虑灵活性需求与新能源不确定性的IES 规划配置模型求解流程图见附录A 图A1。首先，处理新能源出力的不确定性，取全年WT 和PV 出力历史数据，利用高斯核密度函数和Frank-Copula 函数生成具有相关性的风光日出力曲线，通过聚类的方法得到典型日风光出力；然后对需求响应不确定因素进行处理，以日前多能负荷预测数据为基准，改变电价方案，计算得到不同电价方案下，用户参与IDR 后的多能负荷需求；最后将上述数据以及各设备型号参数作为基础数据输入IES 双层协同优化配置模型中。由3.2节可知，上层模型为整数非线性规划问题且决策变量数量较少，采用遗传算法进行求解；下层模型为混合整数线性规划问题，基于GAMS 建模工具［20］调用求解器进行求解，通过比较所有电价方案下总成本的最优值，输出IES 优化配置结果及优化运行方案，此时的电价方案即为最优电价方案。

4 算例仿真与分析

4.1 基础数据

本文以南方某园区IES 为例进行仿真分析，其等效结构如图1 所示。由于不同季节用能负荷的差异，分别对夏季和非夏季采取不同峰谷平时段划分方式，具体时段划分见附录A 表A1。为了提高用户参与IDR的积极性，将峰、谷分时电价比设置为5∶1。园区内各备选设备型号及参数见附录A 表A2。各典型日负荷数据见附录A 图A2—A4，其中基本负荷、可削减负荷、可转移负荷、可替代负荷占比为0.6∶0.15∶0.2∶0.05。IES 运营商外部购电价格见附录A 图A5。天然气购买价格恒为2.8 元／m3。碳排放处理成本为0.02元／kg。电能和天然气的碳排放系数μe和μg分别为0.8、0.25 kg／（kW·h）。

4.2 风光出力典型日场景

WT 和PV 的典型日出力（标幺值）曲线如图3 所示，各个场景呈现出明显的季节性与时序性，根据光照强度和风速水平将其划分为夏季、冬季和过渡季，代表相应季节典型日的风光出力情况。为满足综合能源运营商的经济效益并推动“双碳”目标的实现，本文以实际场地最大安装风光机组上限进行规划，即WT与PV容量为定值，取3台WT与2组PV电池。

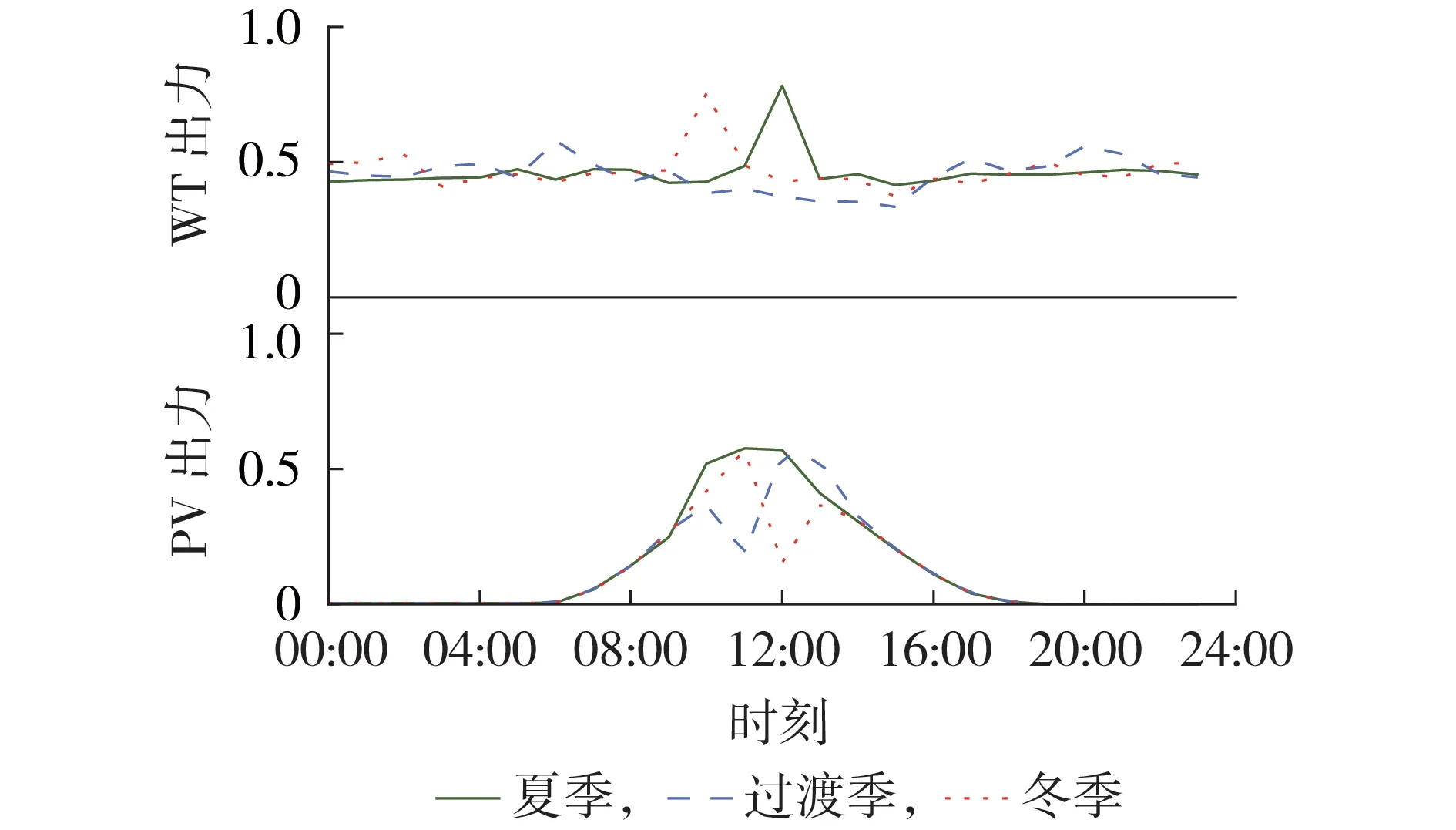
图3 风光出力曲线Fig.3 Wind power and photovoltaic output curves

4.3 风光出力及IDR 不确定性对优化配置结果的影响分析

本节设计了5种场景进行对比分析，见表1。由表可知：场景1 不考虑IDR 对规划模型的影响，即所有负荷均为基本负荷的确定性场景；场景2和场景3分别选取梯形隶属度函数中心点等于-0.2 和-0.7 的Z-number 值表示用户价格弹性水平分别为低和高，并假设其可信度均较高，即三角形隶属度函数选取（0.8，0.9，1）；场景4 选取三角形隶属度函数中心点为0.4 表示此时IDR 相关数据可信度为低；场景5 假设IDR相关数据可信度为完全可信，即忽略数据可信度对IDR的作用，由于ζn，t仅由一个模糊数表示，此时的Z-number 模型等效于传统模糊模型。通过对比场景1—3 可分析不同用户价格敏感度对IES 规划的影响，场景3—5的用户价格弹性水平均为高，但数据可信度不同，因此可对比不同数据准确度对IES配置的影响。需要注意的是，隶属度函数的参数可根据实际案例中不同自然语言的具体描述选取合适的数值分布区间，不同的参数依然适用于本文所提的IES优化配置方法，对本文的分析过程并无影响。

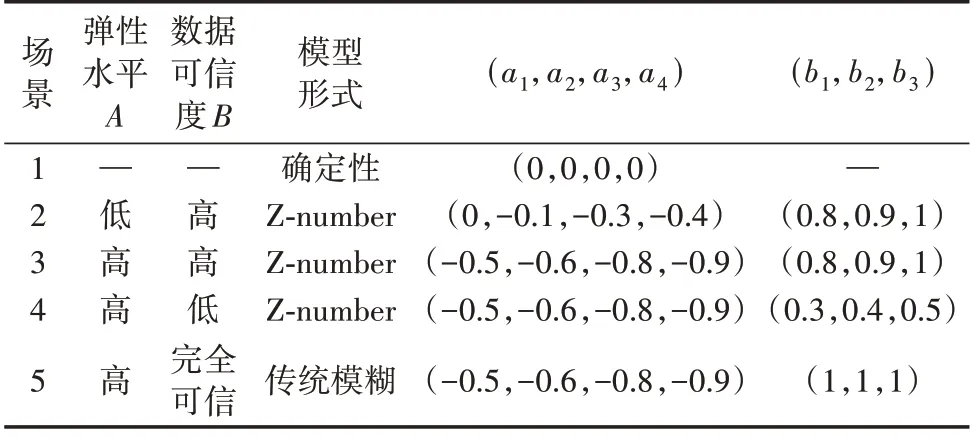
表1 场景设置情况Table 1 Scenario setting situations

应用本文所提规划模型对不同价格弹性场景和不同数据可信度场景下的IES 优化配置方案进行求解，使IES 年化总成本最小的峰、平、谷分时电价分别为1.33、0.8、0.27 元／（kW·h）。各场景优化配置方案及年化成本对比分别见表2、3。各配置方案之间并不存在孰优孰劣之分，而是使用Z-number 方法描述IDR 不确定性后的IES 经济性最优配置方案。由于ISE 和HSE 成本低，有较大盈利空间，其优化结果均为3台Ⅱ型HSE、3台Ⅱ型ISE，即等于其上限容量，因此并未在表中体现。

表2 各场景优化配置方案Table 2 Optimal configuration scheme in each scenario

表3 各场景年化成本对比Table 3 Annual cost comparison in each scenario单位：万元

4.3.1 不同用户价格敏感度对IES规划的影响

为展示IDR 不同用户价格敏感度对IES 规划的影响作用，对比场景1 与场景2，可看出供冷和供热设备总装机容量分别降低了8.84%和6.28%，且由于IDR 的加入，对BT 的需求减少，因此设备初始投资成本减少了22.63 万元。在场景2 中IDR 成本为-10.25万元，表现为收益形式，这是由于用户对价格的灵敏度不高，柔性负荷的改变量少。但峰时段负荷量与电价均处于高位，因此IES运营商考虑IDR后相较于不考虑IDR 以基准电价向用户售电将获得更多收益，但根据场景3 的计算结果可看出IDR 成本会随着用户价格弹性水平的提高，电价峰时段负荷量的降低，最终转化为成本形式。与场景1 相比，场景2 和场景3 总成本分别减少了4.98%和8.64%，这说明IDR 用户价格敏感度的增加能有效提高系统的经济性。

4.3.2 不同数据可信度对IES规划的影响

为表明不同数据可信度对IES 规划的影响，场景5 假设IDR 相关数据可信度为完全可信，此时Z-number 模型等效于传统模糊模型。场景5 的冷、热、电负荷峰值降幅最大且用能总量最少，其设备初始投资成本和外部购能成本均有所降低，即使额外增加了5.12 万元的IDR 成本，总运行成本仍然为5个场景中的最小值。场景4 的用户价格弹性水平为高，但IDR 相关数据可信度为低，负荷峰值和负荷总量的降低程度都不如场景5 明显，在上层规划设备选型时，为了保证系统可靠性，设备安装容量与系统运行成本相应增加。对比场景3—5可知，随着数据可靠程度的降低，由于考虑规划期内不确定性IDR的影响，为保证供能可靠性，各类供能设备初始安装容量增加，IES 年化总成本随之升高。然而，在实际工程中，若不考虑IES 中可能存在的响应度数据可信度问题，会导致配置结果的有效性下降，而应用本文所提方法可在规划过程中计及原始数据可靠程度的影响作用，有助于IES 运营商更加合理地规划设备配置与机组运行，评估IDR的预期效益。

4.4 机组优化出力分析

为分析IDR 参与IES 运行所带来的影响，以夏季场景3 为例，IES 典型日电功率平衡情况见图4，冷、热功率平衡情况分别见附录A图A6和图A7。

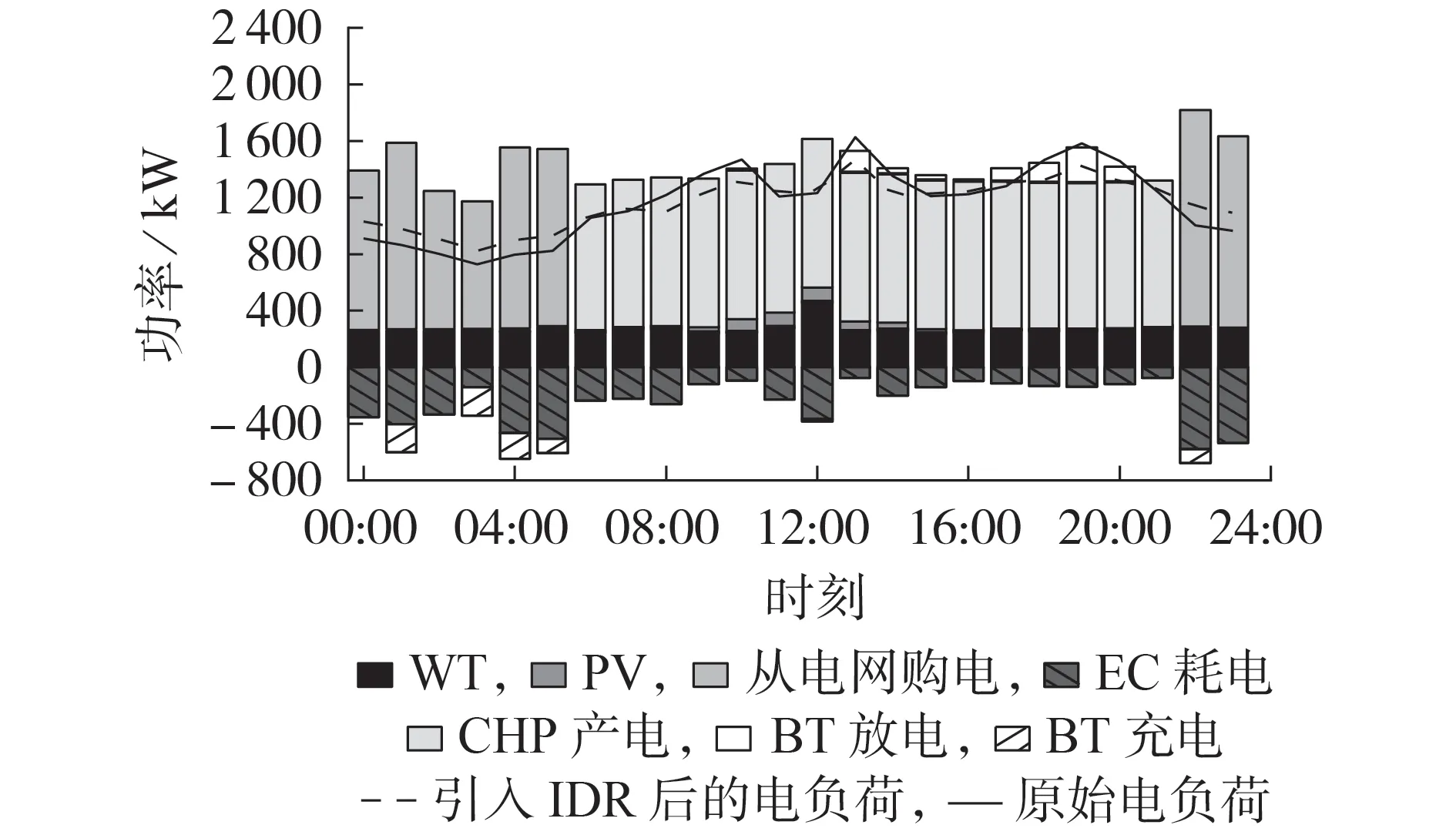
图4 夏季典型日电功率平衡Fig.4 Electric power balance of typical summer day

根据电、冷、热功率平衡情况可以看出，夏季冷负荷需求较高，且峰谷差大，电负荷需求一般，而热负荷需求很低，且波动较小。当用户对价格信息的敏感度和参与IDR 项目的数据可信度均较高时，对比IDR 前后电、冷、热负荷曲线可发现，IDR 参与系统运行可以有效减小冷、热、电负荷峰值，提升谷时段用能总量。可见，用户为减少自身用能成本，各类负荷都将电价峰时段的部分负荷向电价谷时段转移或借助能源转换设备替代为气负荷，以此满足自身用能需求。以夏季冷负荷为例，峰谷差由1 540.55 kW 减小至1 155.07 kW。相较于引入IDR前，各类负荷曲线更加平缓，有助于维持系统平稳运行。

1）在00:00—06:00、22:00—24:00 时段内，风光出力较小，此时电负荷的功率缺额通过向外部电网购电获得；冷负荷虽处于当日平值时段或谷值时段，但需求水平仍然较高，此时冷负荷由EC 和ISE 供给，确保冷负荷的供需平衡；由于夏季夜间热负荷需求很低，为减轻IES 运营商的运行成本，此时不启动CHP 机组或GB 等制热设备，热负荷由HSE 供给即可满足。

2）在06:00—22:00时段内，风光出力不断增加，此时电价处于平时段或峰时段，系统通过CHP 机组进行发电，CHP 机组满功率运行，满足电负荷与EC耗电功率的同时产生大量的热能，远远超过热负荷及HSE 的消纳能力，与此同时冷负荷又处于当日的峰值时段，因此优先利用AC 将多余热能转化为冷能，若AC 仍无法满足冷负荷需求，剩余部分再由EC或ISE 供给。可以看到，引入IDR 及配置储能系统后，储能装置的运行方式符合“低充高放”的策略，更有利于降低IES的购能成本。

5 结论

本文提出一种考虑灵活性需求与新能源不确定性的园区IES 双层协同优化配置模型，基于本文仿真结果，对比分析不同场景下的IES 配置情况，结果表明IDR 用户价格敏感度的增加可以减少能源转换设备初始安装容量与投资成本，也可影响储能装置的规划，降低IES 对储电设备的需求。应用本文所提方法可在规划过程中计及原始数据可靠程度的影响作用，有助于IES 运营商更加合理地规划设备配置与机组运行，评估IDR的预期效益。

随着未来能源市场开放程度的提高，多区域IES协同规划问题和多IES 运营商之间的利益博弈是笔者下一步的研究工作。

附录见本刊网络版（http：//www.epae.cn）。