基于改进Wasserstein生成式对抗网络的电力系统不良数据辨识
2022-09-14臧海祥郭镜玮黄蔓云卫志农孙国强赵佳伟
臧海祥,郭镜玮,黄蔓云,卫志农,孙国强,赵佳伟
(河海大学 能源与电气学院,江苏 南京 211100)
0 引言
随着“双碳”目标的提出,大量新能源并网导致电力系统需处理的数据量呈指数级增长,使得电力系统的数据结构越来越复杂[1],因此对系统运行的可靠性、安全性和稳定性提出了更高的要求。由于在实际量测信息中除了含有正常的数据噪声外,各信息采集单元所获取的量测信息中还会出现一定比例的不良数据,不良数据的存在不仅使电力系统的状态估计结果难以反映系统的真实状态,降低电力系统状态估计的收敛性能,还会对电力系统的调度造成困扰[2]。不良数据检测和辨识是电力系统状态估计的重要一环,其功能是在获取系统状态量的基础上依靠采集系统提供的冗余信息,发现和排除采集数据中偶然出现的少量不良数据,以提高状态估计的可靠性[3]。因此,不良数据辨识对状态估计以及电网状态分析具有重要的意义。
传统的不良数据辨识方法包括残差搜索法、非二次准则法、零残差法、估计辨识法[4-5]。文献[6-7]采用线性化残差方程辨识量测中的不良数据。在出现多个不良数据的情况下,上述方法经常会发生误检现象,影响辨识效果,且传统方法普遍采用估计-检测及辨识-再估计的迭代原理,计算量极大,导致在大规模系统中的计算效率很低。为此,有学者将人工智能方法引入不良数据辨识中。文献[8]利用小波系数能反映曲线突兀程度的特点,结合RGB 数值判断不良数据的位置,但该方法对偏差较小的不良数据的辨识性能较差,且在大规模系统中的计算效率较低。为了提高计算效率,文献[9]提出基于Spark 和并行K-means 算法的不良数据辨识方法,克服了易陷入局部收敛和计算时间过长的问题;文献[10]提出将双馈深度学习方法用于线性状态估计中的不良数据辨识,具有更高的辨识精度且减少了线性状态估计的迭代负担;文献[11]提取监测数据的特征量,并基于预先设置的时序变化量矩阵和时序数值矩阵进行模式匹配,实现了不良数据的实时辨识。上述方法虽然能提高辨识效率,但对关联不良数据的辨识精度较低。为此,文献[12]基于分析数据之间的加权关系,提出了可以检测偏差较小的不良数据的方法;文献[13]运用证据融合理论确定量测关联度,反映了量测数据出现残差污染和残差淹没的可能性。虽然上述辨识方法对单个不良数据具有良好的辨识效果,但是针对被残差污染的相关量测数据的检测存在一定的漏检率和误检率[14]。鉴于此,本文提出采用数据驱动方法重构实时量测数据,分析当前断面的重构误差并进行不良数据辨识。
数据驱动的基本思想是:基于试验或历史数据建立数据特征与待研究问题之间的联系。与物理建模不同,数据驱动方法避免了对研究对象内部机理的严格分析,通过大量的测试积累来反映数据特征,挖掘特征集合和目标集合之间的潜在联系,实现电力系统特征量x到代求变量y的映射。本文的数据驱动方法采用生成式对抗网络GAN(Generative Adversarial Network),利用深度学习方法对实时量测数据进行重构,进而辨识不良数据位置。
GAN[15]是一种无监督的深度学习网络,其基于无监督学习获取数据间的潜在特征联系,并生成符合相应分布规律的“伪数据”。目前已有研究将GAN 模型应用于电力系统分析中:文献[16]采用Wasserstein 生成式对抗网络WGAN(Wasserstein Generative Adversarial Network)模型和二值掩码对缺失量测数据进行有效重建;文献[17]考虑到风光资源的不确定性,提出了一种基于WGAN 的风光资源场景模拟和改进时序生产模拟的新能源电源容量配置模型。
为了提高在大电网下不良数据的辨识性能和效率,本文提出了一种基于改进Wasserstein 生成式对抗网络WGAN-GP(Wasserstein Generative Adversarial Network with Gradient Penalty)的电力系统不良数据辨识方法,主要包括以下2 个阶段:①利用历史数据库中的状态量得到多断面正常量测数据并训练WGAN-GP 模型,将量测数据输入已训练完成的WGAN-GP 模型得到对应的量测重构数据和重构误差;②基于上述得到的量测重构误差训练决策树模型以确定不良数据阈值,将实时重构误差输入已训练完成的决策树模型即可辨识1 组量测信息中的不良数据。值得说明的是,若考虑电网拓扑的时变性,则可利用文献[18]中的迁移学习方法,以解决拓扑变化后本文模型出现辨识性能下降的问题。
1 基于WGAN-GP的不良数据辨识
1.1 GAN模型
GAN 是一种深度生成模型,由判别模块和生成模块构成,其结构示意图见附录A 图A1。在训练过程中,生成器G输入与目标数据同维度的高斯噪声,判别器D 输入正常量测信息和生成器输出的伪数据,二者交替迭代训练形成博弈对抗,最终生成器和判别器达到纳什均衡,此时生成器输出重构量测数据。
1.2 WGAN-GP模型的基本原理
传统的GAN 模型采用JS(Jensen-Shannon)散度优化训练参数,其生成器的输入数据为高斯噪声,损失函数可以表示为:
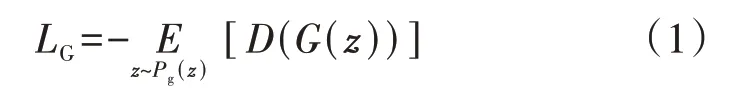
式中:LG为生成器的损失函数;E[·]为期望函数;G(·)为生成器函数;D(·)为判别器函数;Pg(·)为噪声数据分布;z为输入的噪声数据向量。
判别器的输入数据为生成的伪数据以及目标数

然而,在实际应用中WGAN 经常会出现梯度爆炸和不收敛的情况,因此本文在原网络损失函数的基础上加入惩罚项,实现Lipschitz 约束,以弥补WGAN 的缺陷。WGAN-GP 模型的损失函数L(G,D)可表示为:

在模型的训练过程中,选用Adam 优化器通过分别迭代L(G,D)和LG以优化判别器和生成器的参数。
在WGAN-GP 模型的训练过程中,生成器输入与量测信息同维度的高斯噪声,以正常量测信息作为目标数据,判别器和生成器基于式(5)所示损失函数进行博弈对抗训练。最终所得训练充分的模型可以反映正常量测数据的本质特征,在线应用时可以重构实时量测,重构后的数据分布与正常量测数据相似。
2 基于决策树的不良数据阈值确定
2.1 数据预处理
在构建决策树模型的数据集时,本文基于已获得的重构数据计算多断面重构误差,见式(7)。

2.2 C4.5决策树模型的基本流程
C4.5 决策树模型的基本原理见附录B,整体流程图如图1所示[21-22]。
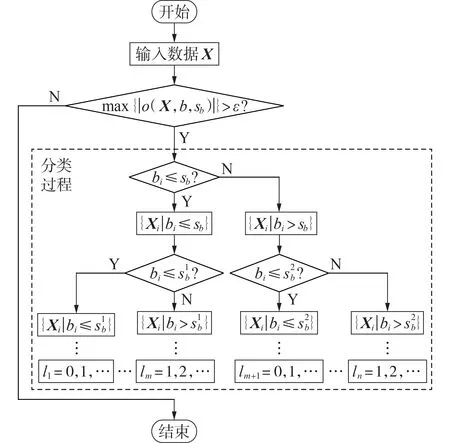
图1 决策树模型的流程图Fig.1 Flowchart of decision tree model

3 基于改进WGAN的不良数据辨识方法
大规模电力系统的运行工况复杂,现有不良数据辨识方法难以应对庞大的数据量和复杂的数据结构,容易出现较高的漏检率和误检率。为此,本文在WGAN-GP模型的基础上,加入决策树模型确定不良数据阈值。具体的不良数据辨识流程图如图2 所示,具体步骤见附录C。
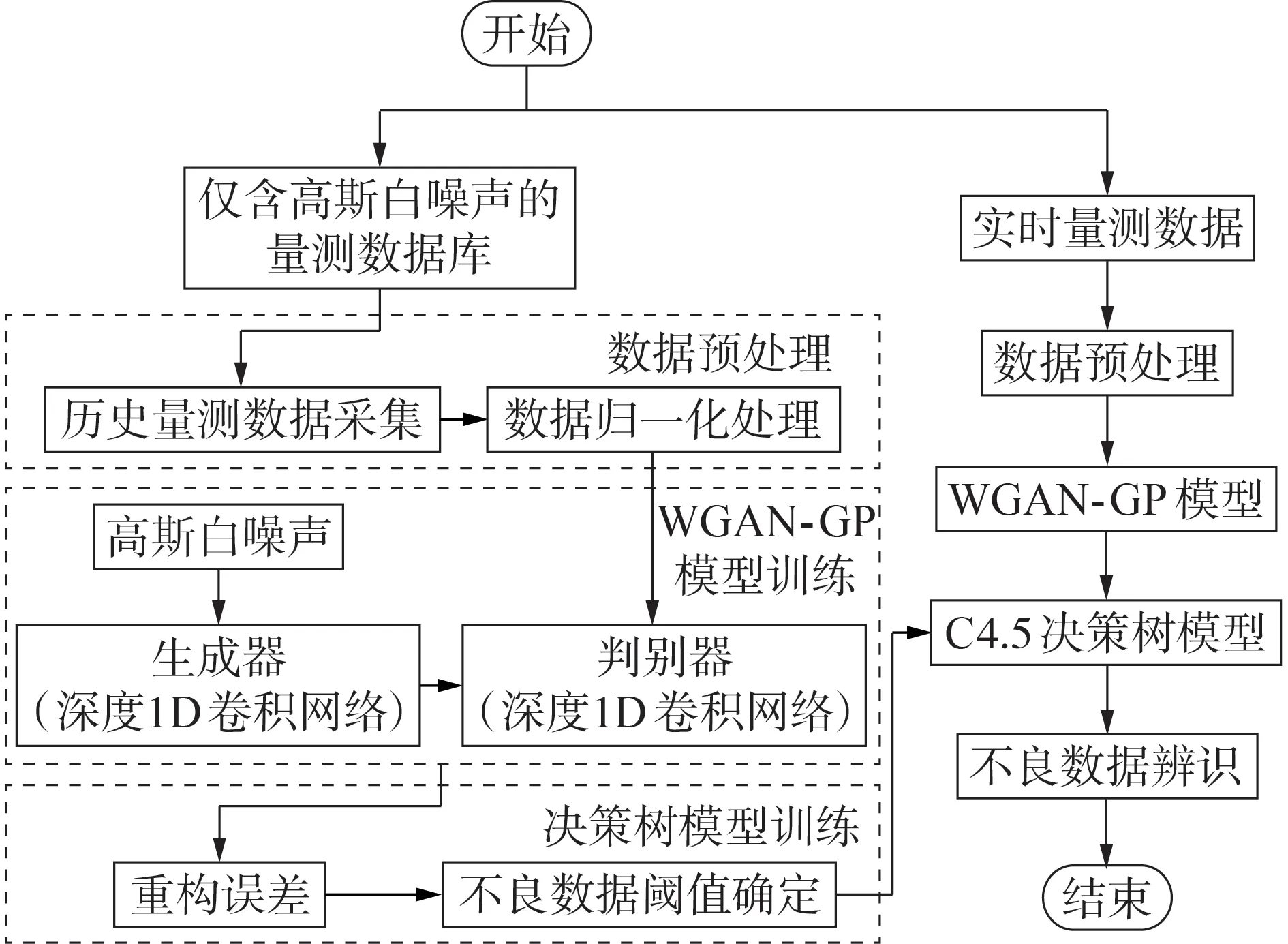
图2 不良数据辨识流程图Fig.2 Flowchart of identifying bad data
4 算例分析
为了验证本文所提方法在大规模电力系统中的优越性,基于Pytorch 搭建WGAN-GP 模型和决策树模型,模型的基本结构和参数设置见附录D 表D1和表D2。本文测试环境为PC 机,处理器为Intel®CoreTMi7-8700K CPU@3.70 GHz,内存为16.0 GB。
4.1 数据集生成
基于IEEE 118 节点系统测试本文所提方法的性能。为了能更适应系统的真实运行情况,首先利用某省网连续800 h的实际运行数据获取负荷曲线,以此模拟IEEE 118 节点系统中各节点的负荷变化,然后通过传统潮流计算方法得到多断面潮流真值,最后在潮流计算值的基础上添加高斯白噪声,生成历史多断面的量测数据,从而形成历史量测数据库。其中量测信息包括节点电压幅值及支路首/末端功率。将量测数据集按照6∶4 的比例分配为训练集、测试集,并在测试集中选择3%~10%的量测数据加入混合噪声以模拟量测不良数据。其中不良数据的模拟方式为:将正常功率量测增大或减小50%~200%,将正常电压量测增大或减小15%~25%。为了提高模型的训练效率,分别对电压幅值和支路功率进行建模,在保证模型性能的同时提高模型的训练效率。
不良数据的分布图见附录D 图D1。不良数据的位置见附录D 图D2。利用测试集数据与模型重构数据得到多断面重构误差,将重构误差按照7∶3的比例划分决策树模型的训练集和测试集,并按该比例划分历史量测数据库并进行模型训练。
4.2 WGAN-GP模型的性能测试
本文所提方法的关键是WGAN-GP 模型的重构性能,为了更直观地体现模型的性能,本文利用t-SNE 可视化算法将生成的高维数据映射到低维空间中并保留数据集的局部特征。
IEEE 118节点系统实时量测、潮流真值、重构数据基于t-SNE 可视化算法的数据分布结果见附录D图D3。由图可以看出,基于WGAN-GP 模型得到的重构数据分布与潮流真值分布接近,由于实时量测数据中包含一定比例的不良数据,在降维处理后,其数据分布与潮流真值分布差距过大,但是在训练WGAN-GP模型时,选取正常量测数据作为判别器的输入,使判别器学习得到目标数据样本的分布规律,在状态空间中生成全新有效的重构数据。为了验证WGAN-GP模型在实际电网中的性能,将其用于测试某省级电网的数据,测试结果见附录D图D4。
为了定量测试WGAN-GP 模型的性能,本文采用2-范数误差γTNE对重构数据和量测数据进行分析,其计算公式为:

不同测试系统的2-范数误差(标幺值)如表1 所示。由表可知,将测试集的量测数据输入WGAN-GP模型后,重构数据更加接近潮流真值。训练完成的WGAN-GP模型可以重构实时量测数据,得到的数据与原数据相比更接近正常量测信息,可实现量测信息的特征提取,以便后续准确辨识不良数据的位置。以某省级电网和IEEE 2 383 节点系统为例,与实时量测相比,重构数据的2-范数误差分别降低了94.67%和93.11%。

表1 不同测试系统的2-范数误差Table 1 Two-norm error of different test systems
4.3 不良数据辨识性能测试
为了更直观地体现本文所提方法的优越性,将残差搜索法、模糊C 均值FCM(Fuzzy C-means)算法、支持向量机SVM(Support Vector Machine)算法作为对比方法。由于仅靠不良数据的漏检率和误检率无法有效地评估模型的性能,本文采用查全率和查准率衡量不良数据辨识模型的性能,其计算公式分别为:

式中:μTPR为查全率,其值表示辨识为正常数据的正确结果在正常数据样本中所占的比例;μTFR为查准率,其值表示辨识为不良数据的正确结果在所有不良数据样本中所占的比例;μAcc为总体准确率;φTP为实际为正常数据且辨识结果为正常数据的样本数量;φFN为实际为正常数据但辨识结果为不良数据的样本数量;φTN为实际为不良数据且辨识结果为不良数据的样本数量;φFP为实际为不良数据但辨识结果为正常数据的样本数量。
当不良数据比例不同时,本文所提方法的辨识性能结果如表2 所示。由表可以看出,本文所提方法的查全率、查准率、总体准确率指标均在95%以上,且不良数据比例对整体模型辨识性能的影响较小,当不良数据比例达到20%时,本文所提方法依然有较高的准确性。
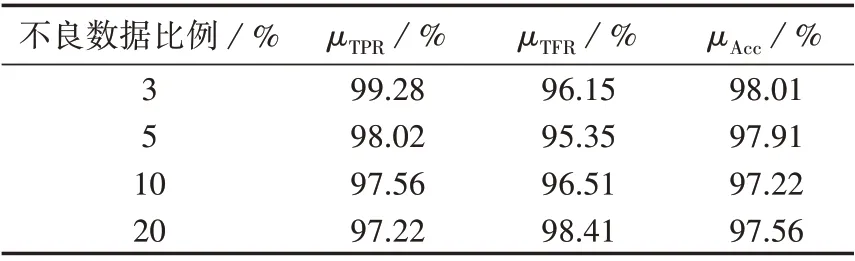
表2 本文所提方法的辨识性能结果Table 2 Identification performance results of proposed method
为了体现本文所提方法的优越性,比较各方法在不同不良数据比例下的总体准确率,如图3 所示。由图可看出:随着不良数据比例的增大,残差搜索法的总体准确率下降较为明显;FCM 算法采用相似度大小划分数据类别,随着不良数据比例的增大,会将正常数据误判为不良数据;SVM 算法无法学习所有不良数据的特征,因此在实际应用中会出现较大的漏检率;而随着不良数据比例的增大,本文所提方法的总体准确率均在95%以上。以不良数据比例为20%为例:相较于残差搜索法,本文所提方法的总体准确率提升了20.9%;相较于SVM 算法和FCM 算法,本文所提方法的总体准确率分别提升了7.67%和4.73%。

图3 不同辨识方法的总体准确率Fig.3 Overall accuracy rate of different identification methods
上述不良数据设置并没有包含由量测残差污染引起的关联不良数据。为此,人为设置多个单个不良数据和关联不良数据,不同不良数据设置下IEEE 118 节点系统的辨识结果如图4 所示。图中,节点电压幅值、支路首端有功功率、支路首端无功功率均为标幺值。
由图4 可以看出,当实时量测数据偏离正常量测区域较大时,对比方法和本文所提方法均可有效识别不良数据,但SVM 算法和残差搜索法无法识别接近正常值的不良数据,当不良数据的偏差较小时,其与正常数据密切相关,因此不良数据很容易被视为正常数据。由于FCM 算法基于相似度大小划分数据类型,当出现连续不良数据且中间数据的振幅与前后数据相似时,FCM 算法会将该数据误判为正常数据。而本文所提方法通过提取数据本质对数据类型进行划分,当出现量测残差污染时,仍具有较好的辨识性能。本文所提方法对实时量测进行重构,重构后的数据更接近不含不良数据时的量测信息,因此训练好的WGAN-GP 模型可以学习到数据特征,当量测信息中含有杠杆量测时,本文所提方法仍具有较好的辨识性能。
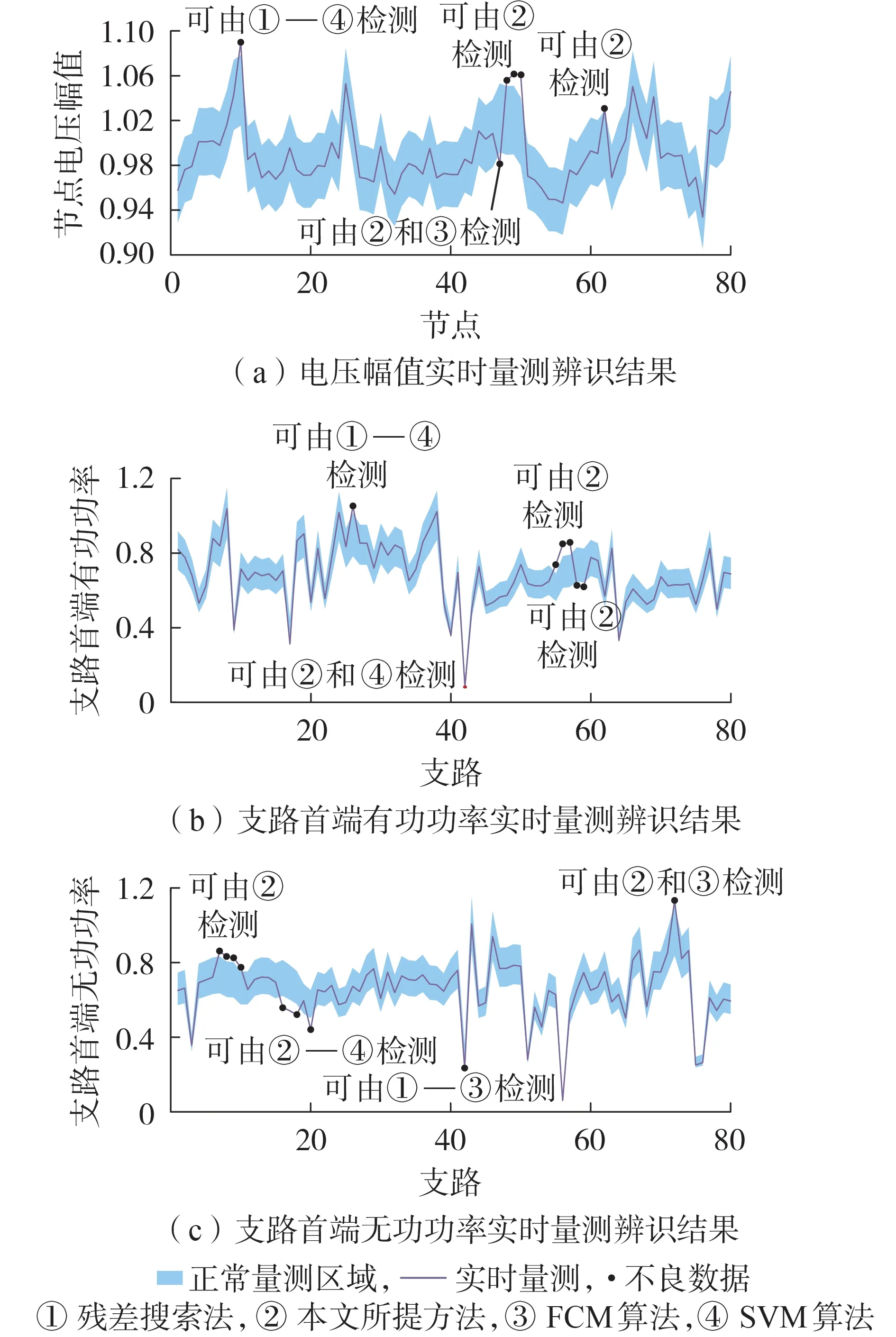
图4 IEEE 118节点系统在不同不良数据设置下的辨识结果Fig.4 Identification results of IEEE 118-bus system under different settings of bad data
为了更直观地展现本文所提方法在不同不良数据设置下的辨识精度,对IEEE 118 节点系统设置单个离群值、由量测残差污染导致的关联不良数据、杠杆量测等不良数据。不同不良数据设置下的辨识结果如表3 所示。由表可知,本文所提方法在经过数据特征提取和学习后,能够适应不同类型的不良数据,因此当含有关联不良数据和杠杆量测时,本文所提方法仍具有较高的总体准确率,避免在存在多个杠杆量测时出现漏检和误检。

表3 不同不良数据设置下的辨识结果Table 3 Identification results under different settings of bad data
为了能更直观地体现不同方法的辨识性能,图5 给出了不同辨识方法在不同不良数据设置下的查准率。由图可看出:残差搜索法在3 种不良数据设置下的查准率均低于70%,且当出现杠杆量测时,残差搜索法只能识别部分与正常数据偏差较大的量测数据;FCM算法利用模糊隶属度判别不良数据,因此FCM 算法对离群值有较好的辨识性能,但是容易将关联不良数据辨识为正常数据,且当量测信息为杠杆量测时,FCM 算法也会对部分杠杆量测造成误判;SVM算法不能学习所有不良数据特征,经常出现漏判现象;本文所提方法在3 种不良数据设置下的查准率均在80%以上,验证了在不同的不良数据情形下本文所提方法的优越性。

图5 不同辨识方法的查准率Fig.5 Precision ratio of different identification methods
为了验证本文所提方法在不同测试系统下的辨识性能,表4 给出了不同测试系统的不良数据辨识结果,其中不良数据比例为15%,节点电压幅值与支路功率按照3∶7 的比例进行分配。由表可以看出:本文所提方法在不同测试系统中的总体准确率均在95%以上;以某省级电网为例,相较于残差搜索法、FCM 算法、SVM 算法,本文所提方法的总体准确率分别提高了14.99%、11.26%、10.58%。可见,将本文所提方法应用于大规模电力系统具有较高的辨识精度。
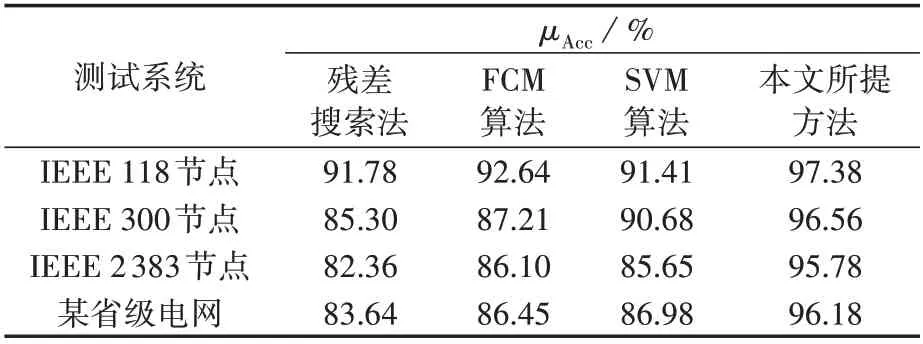
表4 不同辨识方法的总体准确率Table 4 Overall accuracy rate of different identification methods
4.4 不良数据辨识效率测试
传统不良数据辨识方法的基本原理是基于状态估计、检测及辨识、再估计的迭代过程,受系统规模和不良数据比例的影响较大,尤其是在大电网下的计算效率明显下降。但数据驱动方法仅在离线训练时受系统规模的影响较大,在线应用时受系统规模是影响较小,因此,本文所提基于改进WGAN 的不良数据辨识方法不仅能提高在大电网下的辨识性能,也能提升其辨识效率。
表5 给出了不同辨识方法在各测试系统下的辨识耗时。由于残差搜索法在大规模系统中耗时过长,将不良数据设置为2 个节点电压幅值不良数据和8个支路功率不良数据。由表5可以看出:随着系统规模增大,残差搜索法的耗时明显增长,尤其是在IEEE 13 659 节点系统中,残差搜索法的辨识效率已经超出适用范围;以某省级电网为例,本文所提方法的辨识效率相较于残差搜索法有很大的提升,与已有数据驱动算法的耗时相近,但本文所提方法可以在提升辨识性能的同时兼顾辨识效率。
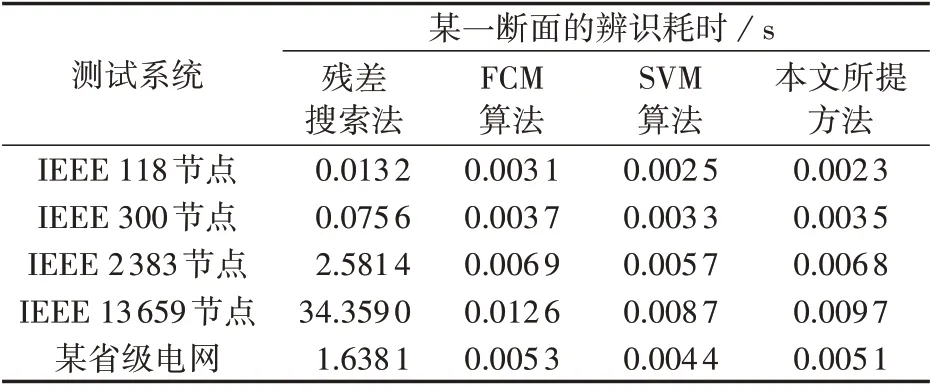
表5 不同辨识方法的辨识耗时Table 5 Identification time-consuming of different identification methods
5 结论
本文构建了改进WGAN 模型,将实时量测数据输入训练完成的WGAN-GP 模型,重构量测数据,并采用C4.5 决策树模型确定不良数据阈值。基于测试算例结果可得如下结论:
1)采用改进WGAN 模型重构量测信息,实现对正常量测信息的特征提取,基于对重构误差的辨识提高了不良数据辨识结果的查全率和查准率;
2)为了避免人为设置不良数据阈值导致的高漏检率和误检率,提出了基于C4.5 决策树模型的机器学习方法,提高了辨识精度;
3)本文所提方法在大规模电力系统中有较好的辨识性能和辨识效率。
后续工作中将考虑拓扑变化对数据驱动模型的影响,将迁移学习技术引入不良数据辨识领域,考虑拓扑信息并重构数据集,提高数据驱动模型的泛化性能。
附录见本刊网络版(http://www.epae.cn)。
