直流频率限制控制器参数多目标双层优化设计方法

2022-09-14王渝红邰克强于光远尹爱辉陈立维

电力自动化设备 2022年9期

王渝红，朱杰，曾琦，邰克强，于光远，尹爱辉，陈立维

（1. 四川大学电气工程学院，四川成都 610065；2. 国网山东省电力公司济南供电公司，山东济南 250000）

0 引言

大规模电网之间通过直流联接实现异步运行，有效改善了区域电网间的低频振荡问题。但异步联接后送端电网网架规模减小、负荷频率调节能力减弱，转动惯量大幅降低，导致异步后送端电网的频率波动远大于联网系统［1］。同时，送端电网（如云南电网、西南电网）为抑制超低频振荡，调整了大型水轮机调速器参数，削弱了水电机组的一次调频能力［2］。因此云南电网和西南电网除常规机组参与一次调频外，均启用了直流频率限制控制器（FLC）功能参与电网频率调控［3］。

直流FLC是高压直流输电系统的一种附加频率控制。送端电网启用直流FLC 功能后，直流FLC 能够根据送端电网频率变化迅速且准确地调节直流输送功率，辅助电网一次调频，极大地改善了送端电网的频率特性［4］，在工程中得到了应用。直流FLC 的控制器结构与机组调速器相类似，主要由限幅、滤波、死区和控制这4 个环节构成。其中，死区和控制环节共同决定着直流FLC的动作特性和频率调节效果，是直流FLC 设计的关键。文献［5］提出了直流FLC 死区和控制环节参数的设计原则，指出直流FLC 的参数设计应兼顾其频率调节效果和动作特性。文献［6-7］通过时域仿真的方法，针对特定的直流输电工程设计了直流FLC 的参数，但在参数整定时并未量化考虑直流FLC 的动作特性。文献［8］基于实际工程的运行经验设计直流FLC 的参数，但参数在不同工况下的适应性还有待进一步验证。文献［9］利用工程试凑法整定直流FLC的控制环节参数，并基于时域仿真方法综合考虑直流FLC对系统频率峰值的抑制程度和功率调节量设计直流FLC的死区参数。文献［10］将人工智能方法应用到直流FLC的参数设计中，但仅优化设计了直流FLC 的控制环节参数，忽略了直流FLC死区参数的设计。

以上研究表明，对于直流FLC 死区和控制环节参数的整定，工程中常利用时域仿真法选择或凭借工程经验试凑，难以保证直流FLC的控制效果最优。而且，现有的研究都侧重于直流FLC 对频率的调节效果，忽视了对直流FLC 动作特性的量化考虑。此外，直流FLC动作将给直流受端电网带来功率扰动，进而影响受端电网频率［11］。

基于以上背景，本文提出了一种直流FLC 参数多目标双层优化设计方法。首先，分析了直流FLC死区和控制环节参数对直流FLC 频率调节特性的影响。在此基础上，兼顾直流FLC的频率调节效果、动作特性以及对受端电网频率的影响程度多个目标，建立了直流FLC 参数双层优化模型。然后，利用进化算法分层递进求解双层模型，实现了对直流FLC 参数的综合最优设计。最后，基于MATLAB／Simulink平台搭建2区域4机直流异步互联模型，仿真验证了所提方法的有效性。

1 直流FLC频率调节特性分析

工程中常用的直流FLC 结构如附录A 图A1 所示［5］。直流FLC 的控制环节可基于一阶惯性环节或比例积分（PI）环节设计。无论采用哪种控制方案设计，直流FLC 的频率调节效果和动作特性都将受其参数的影响。

假设直流异步互联送端电网在t0时刻发生功率盈余扰动，忽略电网结构的影响仅考虑系统惯性中心频率，则扰动后送端电网的频率变化可由发电机转子运动方程表示［12］：

式中：Hsys为系统等效惯量；Δf(t)为系统频率偏差；ΔPm(t)和ΔPe(t)分别为系统机械、电磁功率变化量；Si和Hi分别为机组i的额定容量和惯量；N为系统内参与频率响应的机组数量。

假设在t0时刻送端电网存在的不平衡功率为Plost，则扰动瞬间送端电网的初始频率变化率R0可表示为［12］：

图1 给出了送端电网在功率盈余扰动下的频率和直流FLC功率调节量的变化过程。图中：0.033 Hz、0.050 Hz 和f+db分别为汽轮机、水轮机调速器和直流FLC 的死区上限值［13］；t1—t3为系统频率达到各死区上限值所对应的时刻；fpeak为频率峰值；tp为频率达到峰值的时刻；ΔPFLC(t)为直流FLC 的功率调节量；kFLC为直流功率变化的近似斜率，其大小与直流FLC控制环节的参数有关。由图可知，在［t0，t1］时段内，系统频率偏差还未到一次调频的最低动作门槛，此时有：

图1 直流FLC响应出力和相应的频率偏移Fig.1 Response output and corresponding frequency deviation of DC FLC

当系统频率偏差达到0.033 Hz 时，调速器将动作。实际电网中各水电、火电机组调速器性能和参数设置存在差异，使各机组并非同等程度地参与电网的频率调节。为简化分析，本文忽略同类型机组间一次调频特性的差异，将所有同类型机组视为1台机组。考虑原动机调速器在扰动发生后短时间内的频率响应出力可近似呈线性变化［14］，假设汽轮机和水轮机调速器的变化速率分别为kst和khy，则在(t1，t3]时段内式（1）可改写为：

式中：kgen为发电机调速器的总变化速率。式（6）是扰动发生后送端电网频率关于时间变化的一阶微分方程，将式（6）进行积分运算后，可得送端电网频率在(t3，tp]时段内随时间变化的代数方程为：

t3的具体计算过程见附录B。综合式（5）、（9）可以计算出(t3，tp]时段内，直流FLC的功率调节量为：

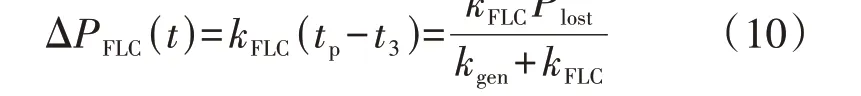
式（9）和式（10）给出了功率盈余情况下送端电网频率峰值和功率调节量与直流FLC各参数之间的关系。频率突增及频率突减工况下送端电网频率峰值和功率调节量与直流FLC各参数之间的关系见附录C。

由式（9）可知，直流FLC 死区设置越小，其调节速率越快，送端电网在大功率阶跃扰动下的频率变化峰值越小。这与已有文献［15］通过仿真分析得到“直流FLC死区与系统频率峰值基本呈线性关系”的结论相一致。由式（10）可知，直流FLC 调节速率越快，其功率调节量越大。但由于直流FLC 的功率调节量即为对受端电网的功率扰动，当直流FLC 调节速率较快时直流FLC 对受端电网频率的影响程度较大。

为分析直流FLC 各参数对频率稳态值的影响，本文对直流FLC各参数不同取值下送端电网频率的变化过程进行了仿真，仿真结果见附录D 图D1，得到如下结论：直流FLC 控制环节Kp、Ki参数大小对系统频率的稳态值没有影响；直流FLC 的死区参数和功率限幅环节参数大小将影响系统稳态频率，且直流FLC 的死区范围越大，功率限幅环节参数设置越小，系统频率的稳态值越低。

此外，死区参数作为直流FLC的启动门槛，缩小死区范围还将导致直流FLC的动作频次和动作时长增加。以云南电网为例，在云南电网异步试运行的14 d内：直流FLC 死区取［-0.14，0.14］Hz时，云南电网5 回直流FLC 动作频次为66 次；直流FLC 死区取［-0.1，0.1］Hz 时，云南电网5 回直流FLC 动作频次则高达268 次［11］。直流FLC 的频繁动作造成了直流功率长期频繁偏离额定值，直流调压设备分接头和交流滤波设备开关频繁动作，严重影响直流系统的可靠运行和直流设备的使用寿命。

直流FLC 参数与送、受端电网频率以及直流FLC 动作特性间的影响关系可总结如表1 所示，表中“√”表示参数与特征量相关，“×”表示二者无关。若在设计直流FLC参数时仅追求直流FLC对送端电网的频率调节效果，则会增大其对受端电网频率的影响，同时恶化直流FLC的动作特性，影响直流系统的稳定运行。因此，本文从协调直流FLC 的频率调节效果、动作特性以及对受端电网频率影响这3 个方面之间的冲突出发，提出了一种直流FLC 参数双层优化设计方法。

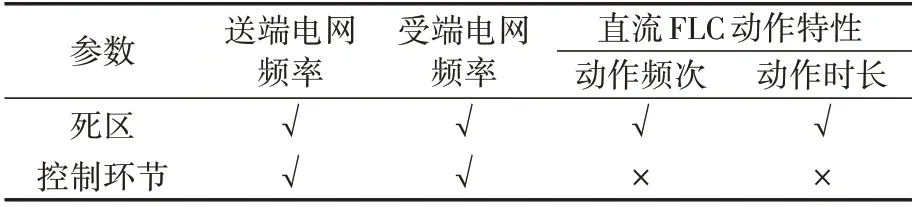
表1 直流FLC参数与各特征量之间的影响关系Table 1 Influence relationship between DC FLC parameters and each characteristic quantity

2 直流FLC参数双层优化设计方法

直流FLC 参数双层优化设计方法如附录D 图D2 所示。送端电网在遭受大功率阶跃扰动时，直流FLC 应首先保证对送端电网频率变化峰值的有效抑制，同时尽量降低直流FLC 的功率调节量以减少对受端电网频率的冲击。因此，第一层优化在大功率阶跃扰动工况下，以直流FLC 对送端电网频率的调节效果兼顾对受端电网频率的影响程度最优为目标，设计直流FLC的控制环节参数xc。

2.1 第一层——直流FLC控制环节参数优化层

2.1.1 目标函数

本节以大功率阶跃扰动下送端电网频率和直流FLC 功率调节量这2个时间绝对误差乘积积分ITAE（Integrated Time Absolute Error）指标最小为目标，建立第一层优化目标函数，如式（11）所示。

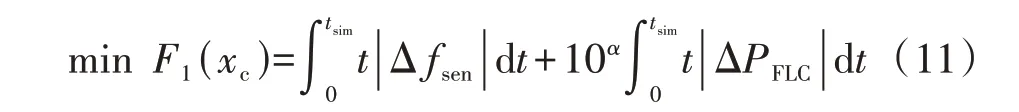
式中：tsim为仿真时长；xc为直流FLC 控制环节参数；Δfsen为送端电网频率偏差；α为数量级调节因子，其值通过考察2 个ITAE 指标的数量级来设定，以避免在优化中出现因数量级差异造成“覆盖”现象。

由于直流FLC 动作时，对受端电网频率造成影响的主要来源是直流FLC 的功率调节量，利用送端电网频率和直流FLC 功率调节量的ITAE 指标，可以综合反映直流FLC对送端电网频率的调节效果以及对受端电网频率的影响程度。

2.1.2 约束条件

第一层优化选择直流FLC的控制环节参数作为优化变量，因此直流FLC 的PI 控制器参数初值需满足如下不等式约束：

直流FLC 作为电网一次调频的辅助手段，对电网频率调节需要与常规机组协调配合完成，避免因直流FLC 动作影响常规机组一次调频的正常动作。因此在优化直流FLC 的控制环节参数时，常规机组的一次调频响应需要满足电网导则要求，即满足：

式中：g1(xc)、g2(xc)为直流FLC 的约束条件，分别对应式（12）、（13）；h(xgen)为常规机组的约束条件，对应式（14）；xgen为常规发电机组变量。

2.2 第二层——直流FLC死区参数优化层

2.2.1 目标函数

第二层优化包含3 个目标。第一个目标为直流FLC 的频率调节效果最好，目标函数为连续小负荷扰动下送端电网频率的标准差最小，如式（16）所示。

式中：Δt为采样时间间隔；ΔPFLC，k为第k次采样时直流FLC的功率调节量。

式（17）直接反映了直流FLC对受端电网频率稳定的影响程度，但受端电网频率变化受直流FLC 功率调节量的影响，所以式（17）还间接反映了直流FLC 每一次动作后引起的直流功率波动大小。式（18）主要反映直流FLC 的动作总时长，但由于直流FLC 动作次数越多，动作时间就会越长，所以式（18）还间接反映了直流FLC的动作频次。

2.2.2 约束条件

第二层优化以直流FLC 的死区参数作为优化变量。实际电网中各调频资源参与一次调频时的投入原则遵循火电机组和水电机组为主、直流FLC 为辅，因此直流FLC 的死区范围应大于火电、水电机组调速器的死区范围。一般情况下，汽轮机调速器死区参数为±0.033 Hz，水轮机调速器死区参数为±0.05 Hz，因此在优化过程中应保证FLC 死区参数绝对值大于0.05 Hz。

此外，直流FLC 死区设置过大可能导致直流FLC 无法及时参与电网频率调控，从而使送端电网在暂态过程中存在频率失稳的可能。为了使送端电网频率满足《电力系统安全稳定导则》的规定［15］，即发生最大N-1故障时保持频率稳定且不会导致低频减载或高频切机动作，本文在电网第一轮低频减载或高频切机的动作阈值的基础上预留一定裕度，设直流FLC 死区上限的最大值为0.5 Hz，死区下限的最小值为-0.5 Hz。综上，直流FLC 的死区参数需满足如下约束：

式中：g3(xc)为对直流FLC 死区参数的约束条件，对应式（19）。

2.3 模型求解方法

2.3.1 第一层模型求解

由式（15）可知，第一层优化为单目标参数优化问题，本文基于时域仿真分析结果，采用粒子群优化（PSO）算法对第一层模型进行求解。

2.3.2 第二层模型求解

由式（21）可知，第二层优化本质上为多目标优化问题。基于分解的多目标进化算法（MOEA／D）与传统基于Pareto的进化算法相比，具有Pareto前沿分布均匀程度高、计算效率高、收敛效果好等优点，近年来被广泛应用于多目标问题的求解［16-17］。因此，本文首先利用MOEA／D 求解第二层死区参数优化模型的Pareto 前沿，再利用基于主观权值修正的熵权贴近度排序法选择最佳折中解。具体求解步骤如下。

1）建立第二层直流FLC死区参数多目标优化模型，如式（21）所示。

2）基于时域仿真分析结果，利用MOEA／D 求解第二层直流FLC 死区参数多目标优化模型的Pareto前沿，MOEA／D的具体步骤参见文献［16］。

3）利用式（22）计算第j（j=1，2，3）个目标的熵权值λj［18］。

式中：Fj，max、Fj，min分别为boj的最大、最小值。

5）利用逼近理想解排序法（TOPSIS）［19］对综合赋权后的各Pareto 解进行排序，选择贴近程度最大的解作为最佳折中解。

3 算例分析

3.1 仿真模型

为了验证本文所提方法的有效性，基于MATLAB／Simulink仿真平台搭建如附录E 图E1 所示的2 区域4 机直流异步互联电网模型。送端电网包含1 台装机容量为900 MW 的水电机组G1和1 台装机容量为300 MW 的火电机组G2，受端电网包含2台为装机容量900 MW 的火电机组G3、G4。水轮机、汽轮机的调速器结构分别见附录E 图E2、E3。异步互联直流系统额定功率为1 000 MW，在整流侧启用基于PI 环节设计的直流FLC 功能。模型其余参数见附录E表E1—E3。

3.2 直流FLC参数优化模型求解

首先针对上述模型建立如式（15）所示的直流FLC 控制环节参数优化模型。在优化过程中，大功率阶跃扰动工况下的阶跃负荷设置为400 W，并利用PSO算法求解。根据待优化模型的决策变量个数可确定粒子群的维度为2，并设粒子群初始规模为50，惯性权重w=0.8，粒子学习因子c1=0.5、c2=0.5，最大迭代次数dmax=100，PI控制器参数的初值Kp，0=Ki，0=2。经过粒子群在不同初始值条件下的多次迭代搜索后，得到直流FLC 的PI 控制器最优控制参数为Kp，optimal=6.40，Ki，optimal=1.55。

完成第一层优化模型的求解后，建立如式（21）所示的直流FLC死区参数优化模型。优化过程中，设连续小负荷扰动下的负荷变化范围为-5%S～5%S（S为送端电网装机容量），持续时间为1 440 min，利用MOEA／D 求解。为验证MOEA／D 的优越性，本文同时利用基于Pareto 进化的优秀算法——快速非支配排序遗传算法（NSGA-Ⅱ）［20］求解FLC 死区参数优化模型，2种算法的种群规模均设置为100，迭代次数均设置为200。经迭代计算后，得到2种算法对应的Pareto 前沿分布分别如附录E 图E4（a）、（b）所示。

与NSGA-Ⅱ相比，MOEA／D 利用权重向量将多目标问题转化为多个协同优化的单目标问题，权重向量在迭代过程中保持均匀分布，能够有效保障最优解在目标空间上的均匀程度。其次，MOEA／D利用外部集合（EP）保存迭代过程中所有的非支配解，避免了迭代过程中最优解的丢失。因此，在图E4（a）、（b）所示的Pareto 前沿的分布上，MOEA／D 的最优解数量明显多于NSGA-Ⅱ，而且分布也更加均匀。除此以外，在计算复杂程度方面，NSGA-Ⅱ的计算复杂程度可表示为O(mN2p)（m为目标函数的数量，Np为种群数量），MOEA／D 的计算复杂程度则为O(mNpTp)（Tp为邻居数量）。由于Tp远小于Np，所以MOEA／D 的计算复杂程度远低于NSGA-Ⅱ，优化过程中在缩短模型求解时间方面具有较大优势。在相同条件下完成对直流FLC死区参数优化模型的求解，采用NSGA-Ⅱ需17 h，采用MOEA／D 则仅需4.5 h。为进一步证明MOEA／D 在计算速度的方面的优越性，本文利用第三代非支配排序遗传算法（NSGA-Ⅲ）和多目标粒子群优化（MOPSO）算法求解直流FLC 死区参数优化模型，求解结果分别见附录E图E4（c）、（d），2种算法所需计算时间分别为19.6 h和11.5 h，与MOEA／D相比，求解速度仍然较慢。

利用熵权法分别计算MOEA／D 和NSGA-Ⅱ下对应的熵权值，MOEA／D中每个目标对应的熵权值分别为λ1=0.291 5、λ2=0.354 1、λ3=0.354 4，NSGA-Ⅱ中每个目标对应的熵权值分别为λ1=0.311 7、λ2=0.342 6、λ3=0.345 7。由2 种算法对应的熵权值可知，F3、F4所包含的决策信息更多。完成熵权值计算后，在主观权值的修正下利用TOPSIS分别对MOEA／D和NSGA-Ⅱ加权后的Pareto 解进行排序，得到2种算法对应的最佳折中解及目标函数值如表2所示。表中，M、N分别表示MOEA／D、NSGA-Ⅱ的最佳折中解。

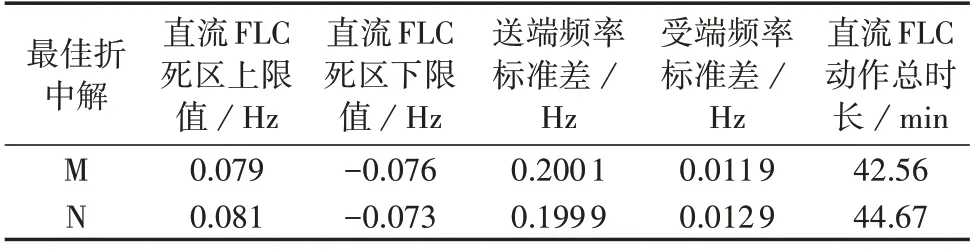
表2 不同算法下的最佳折中解对比Table 2 Comparison of optimal solution under different algorithms

首先从目标函数值来看，2 种方法求解的最佳折中解关于送端电网频率标准差的求取结果相差不大，但关于受端电网频率标准差和FLC 动作总时长这2 个求取结果，最佳折中解M 比最佳折中解N 分别减少了0.001 Hz和2.11 min，可见最佳折中解M对受端电网频率和直流系统造成的附加影响更小。其次，最佳折中解N对应的死区上、下限绝对值之差为0.008 Hz，最佳折中解M 对应的死区上、下限值的绝对值之差则仅为0.003 Hz，可见最佳折中解M 能够在一定程度上保证对频率升高和跌落的均衡抑制，更有利于对系统的频率特性的均衡改善。

综上所述，MOEA／D 在模型求解速度和Pareto解质量上均优于NSGA-Ⅱ。选择MOEA／D 对应的最佳折中解M 作为FLC 的最优死区参数，结合第一层优化的结果，可以得到直流FLC 参数的优化结果如附录E表E4所示。

3.3 大功率阶跃扰动工况

在系统中加入300 MW 的阶跃负荷扰动，在保持直流FLC 限幅及滤波环节参数一致的前提下，采用本文优化设计的直流FLC死区和控制环节参数与文献［15］中基于工程实验试凑法整定的直流FLC死区和控制环节参数（具体参数见附录E 表E4）进行仿真对比，分析直流FLC 在大功率阶跃扰动工况下的频率调节特性。图2 给出了大功率阶跃扰动工况下，送、受端电网实测频率（fsen、frec）和直流FLC 功率调节量的变化趋势，表3 给出了送、受端电网频率变化峰值、直流FLC功率调节量的峰值和稳态值。

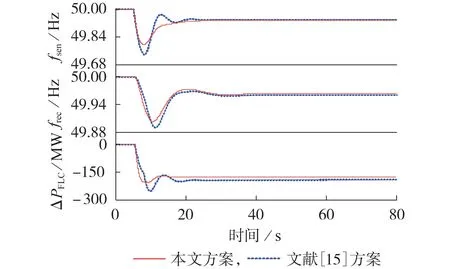
图2 大功率阶跃扰动下仿真结果Fig.2 Simulative results under large power step disturbance

表3 大功率阶跃扰动下不同直流FLC参数优化方案的特征量对比Table 3 Comparison of characteristic quantities of different optimal schemes of DC FLC parameters under large power step disturbance

由表3 可知，与文献［15］中基于工程实验试凑法整定的直流FLC 参数相比，采用本文优化设计的直流FLC 参数时，在大功率阶跃扰动工况下送端电网的频率峰值减小了0.07 Hz，受端电网的频率峰值减小了0.02 Hz，直流FLC 功率调节量的峰值和稳态值分别减少了46.57、13.39 MW。可见，利用本文方法优化设计直流FLC 参数后，直流FLC 在大功率阶跃扰动工况下对送端电网频率峰值的抑制能力有明显提升，同时直流FLC功率调节量有所减小，因此对受端电网频率的影响程度也有所降低。采用不同直流FLC参数设计方案时，在大功率阶跃扰动工况下，送端电网经过一次调频作用后的稳态频率均能恢复至频率允许波动范围以内，即fN±0.2 Hz。

图3 给出了大功率阶跃扰动下，送端电网G1、G2的一次调频响应出力变化。由图可知，相较于文献［15］方案，采用本文所提参数优化方案后G1、G2一次调频响应出力ΔPG1、ΔPG2的峰值均较小，这是由于采用本文所提方案后直流FLC 的响应更加迅速，此时对送端电网频率变化峰值的抑制主要由直流FLC来完成。而且由于直流FLC 响应迅速，缓解了水轮机因突然增加出力造成的水锤效应。此外，在优化过程中直流FLC的死区参数始终保持大于常规机组一次调频死区的约束，根据仿真结果，火电机组、水电机组和直流FLC 参与一次调频的动作时间分别为5.14、5.23、5.40 s，故电网一次调频依旧保持以常规机组为主、直流FLC为辅的配合关系。

图3 大功率阶跃扰动下发电机一次调频出力Fig.3 Output of generator primary frequency regulation under large output step disturbance

为分析直流FLC 功率限幅环节参数对直流FLC频率调节特性的影响，本文在上述仿真分析的基础上增加了不同直流FLC 有功功率限幅参数情况（见附录E 表E5）的仿真对比，仿真结果如附录E 图E5所示。由图可知，由于减小了有功功率限幅参数，不同直流FLC参数设计方案下的直流FLC的功率调节量均被限制在了150 MW，无法完全释放其调节能力。因此，不同直流FLC参数设计方案下的受端电网频率变化峰值较之前相比均有所减小，送端电网频率峰值变化量较之前均有所增加，但采用本文所提方案对送端电网频率峰值的抑制效果仍优于文献［15］方案。不同直流FLC参数设计方案下的送端电网在一次调频后的频率稳态值均为49.92 Hz，可见，本文所提直流FLC参数优化方案在有功功率限幅参数减小的情况下依旧能够保持较好的频率调节性能。

3.4 连续小负荷扰动工况

在系统中加入如附录E 图E6 所示的连续小负荷扰动，波动范围为-6%S～3%S，持续时间为200 s。在保持直流FLC有功功率限幅及滤波环节参数一致的前提下，将本文优化设计的直流FLC 死区和控制环节参数与文献［15］中基于工程实验试凑法整定的直流FLC 死区和控制环节参数进行仿真对比，分析直流FLC 在连续小负荷扰动工况下的频率调节特性。图4 给出了连续小负荷扰动下，送、受端电网频率和直流FLC 功率调节量的变化趋势，表4 给出了各特征参量的对比情况。

图4 连续小负荷扰动下仿真结果Fig.4 Simulative results under continuous small load disturbance

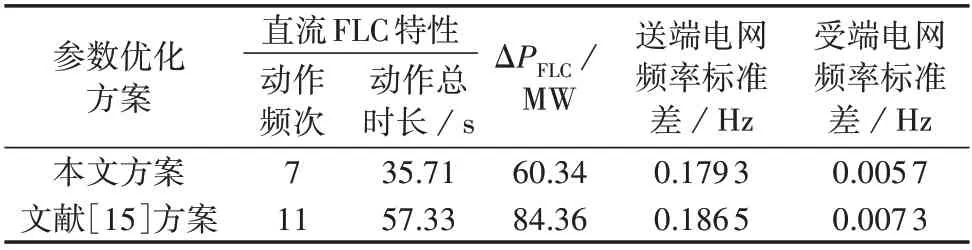
表4 连续小负荷扰动下不同直流FLC参数优化方案的特征量对比Table 4 Comparison of characteristic quantities between different DC FLC parameters optimization schemes under continuous small load disturbance

由表4可知，利用本文所提直流FLC参数优化设计方案，在连续负荷扰动下，送、受端电网频率标准差较文献［15］方案分别降低了0.007 2、0.001 6 Hz。可见利用本文所提直流FLC 参数优化设计方案后，在连续小负荷扰动工况下直流FLC能够保持对送端电网频率的有效调节，同时降低对受端电网频率的影响程度。此外，与文献［15］方案相比，本文所提直流FLC参数优化设计方案中直流FLC的动作频次和动作总时长分别减少了4、21.26 s，改善程度分别为36.36%和37.08%；直流FLC 功率调节量减少了24.02 MW，改善程度为28.47%。可见，利用本文所提直流FLC 参数优化设计方案，能够大幅降低直流FLC 的动作频次和动作时长，减少直流FLC 的功率调节量，使直流FLC的动作特性得到充分改善。