基于自适应干扰观测器的永磁球形电机连续非奇异终端滑模控制

王群京， 刘中阳， 李国丽， 文彦

(1. 安徽大学 电气工程与自动化学院，安徽 合肥 230601；2. 安徽大学 高节能电机及其控制技术国家地方联合实验室，安徽 合肥 230601；3. 安徽大学 工业节电与用电安全安徽省重点实验室，安徽 合肥 230601；4.安徽大学 工业节电与电能质量控制安徽省级协同创新中心，安徽 合肥 230601； 5.安徽大学 互联网学院，安徽 合肥 230601)

0 引 言

传统的多自由度伺服运动装置通常由多台单自由度电机和各种齿轮传动机构组成，这会导致这类多自由度运动系统结构复杂、体积庞大。而永磁球形电机是一种能够在单台电机上实现多自由度运动的特种电机。它具有体积小、响应速度快等优点，在机器人、航空航天等领域具有广阔的应用前景[1]。

为了能够实现永磁球形电机的工业应用，其轨迹跟踪控制问题逐渐成为了研究热点。永磁球形电机作为一个多变量、强耦合的非线性系统，不仅存在建模的误差，还受摩擦、外部扰动等影响[2]。这些未知不利因素使永磁球形电机的高精度轨迹跟踪控制变得十分困难。文献[3-4]把经典的PD控制算法运用到了永磁球形电机轨迹跟踪控制中。虽然PD控制器结构简单且容易设计，但是其动态响应和稳态精度易受未知干扰的影响。为了提高永磁球形电机的跟踪精度，文献[5]提出了一种针对永磁球形电机的计算力矩控制策略。然而，计算力矩控制策略的性能依赖于永磁球形电机名义动力学模型的精确程度。为了降低对永磁球形电机名义动力学模型的依赖，智能算法被逐渐用于永磁球形电机的轨迹跟踪控制中。文献[6]提出了一种永磁球形电机的单神经元自适应控制器和基于粒子群算法的神经网络辨识器。文献[7]在永磁球形电机动态解耦控制中增加了模糊控制器和神经网络辨识器。然而，神经网络虽然提高了永磁球形电机的轨迹跟踪性能，但却需要大量的样本训练时间，不利于永磁球形电机的实时控制。而模糊控制虽然具有较强的鲁棒性，但控制信息的模糊化会降低永磁球形电机的跟踪精度。

近年来，滑模控制器由于结构简单、易物理实现、对系统参数变化和外部扰动的低灵敏性，可以较好地保证了系统鲁棒性[8]，被逐渐用于永磁球形电机的高精度轨迹跟踪控制中。文献[9]将基于干扰观测器的永磁球形电机鲁棒滑模控制与模糊控制器相结合，采用模糊逻辑逼近干扰观测器的观测误差和不可观测部分。文献[10]将鲁棒自适应滑模控制与反演控制相结合，并将其运用到永磁球形电机的轨迹跟踪中，提高了永磁球形电机的跟踪性能。文献[11]提出了一种永磁球形电机的鲁棒滑模自适应动态面控制策略，避免了反演控制中的微分爆炸现象。文献[12]在永磁球形电机鲁棒自适应滑模控制的基础上引入了延时补偿。然而，上述这些用于永磁球形电机的滑模控制均采用传统的线性滑模面，这使得系统状态到达滑模面后沿着滑模面是渐近收敛的。近年来，终端滑模控制因具有较高的稳态精度和较强的鲁棒性，被广泛应用于各种高精度的非线性控制系统中[13-15]。终端滑模控制利用非线性滑模面使得系统状态到达滑模面后沿着滑模面是有限时间收敛的[16-18]。本文则针对永磁球形电机提出了一种连续非奇异终端滑模控制，在保证控制率连续非奇异的情况下，实现了永磁球形电机的高精度轨迹跟踪。

在滑模控制中，为了抑制未知复合干扰对控制系统的影响，往往假设复合干扰具有未知的上界并采用保守的切换增益来确保控制系统的稳定性。这会使得控制器的切换增益过大，导致初始控制量过高，增加硬件系统负担，并影响系统的性能[19-20]。为了处理这样的问题，本文首先提出一种改进的自适应干扰观测器来估计永磁球形电机的复合干扰。然后，将复合干扰观测值在连续非奇异终端滑模控制器的前端进行补偿，有效地降低连续非奇异终端滑模控制器的保守性，避免永磁球形电机饱和输出，提高永磁球形电机轨迹跟踪的性能。

1 永磁球形电机的动力学模型和转矩模型

永磁球形电机的CAD模型如图1所示。图2展示了永磁球形电机的实验样机。由图1和图2可知，永磁球形电机主要由定子线圈、定子壳、永磁体、转子体和输出轴构成。转子体是一个半径为65 mm的不导磁球体，并有40个永磁体镶嵌其中。这40个永磁体在转子体上分为4层，且相邻永磁体遵循N、S磁极交替排列。定子线圈与转子体之间具有1 mm的空气气隙。此外，定子壳上共有24个1 200匝的定子线圈，分为两层，关于赤道面对称排列。转子输出轴用来进行力矩传递，根据不同的通电策略可以实现永磁球形电机的横滚、偏航和俯仰3个自由度的运动。

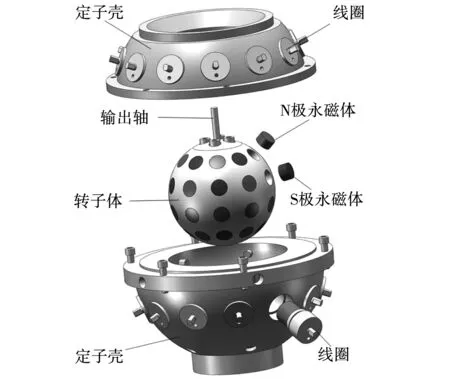
图1 永磁球形电机的整体结构Fig.1 Overall structure of the PMSA

图2 永磁球形电机的样机Fig.2 Prototype of the PMSA

1.1 永磁球形电机的动力学模型

图3展示了定转子坐标变换示意图。利用图3所示的定子坐标系到转子坐标系的旋转变换方式，可以得到描述转子相对定子位置的欧拉角q=[α,β,γ]T。进而，旋转变换矩阵为

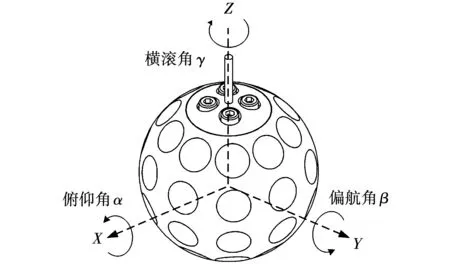
图3 旋转变换Fig.3 Coordinate transformation

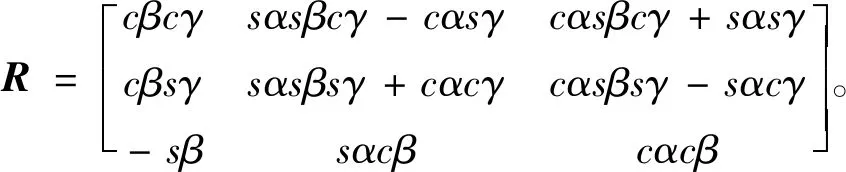
(1)

其中：s表示sin(*)；c表示cos(*)。

因此，可得转子角速度w=[w1,w2,w3]T与欧拉角速度具有转换关系为

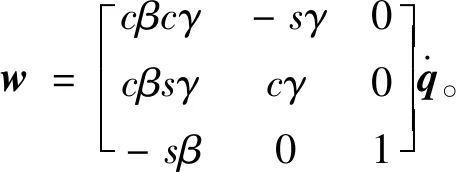
(2)

考虑永磁球形电机的外界干扰，摩擦力矩和模型误差等未知的复合干扰，通过式(2)和拉格朗日第二方程可以获得永磁球形电机动力学方程为

(3)

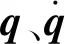
M0(q)的形式为

(4)

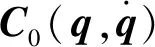
(5)

其中：

(6)

其中：J1=J2=J12=0.015 48 kg·m2和J3=0.015 71 kg·m2是永磁球形电机转子的名义转动惯量，其名义值可由仿真软件得到。

1.2 永磁球形电机的转矩模型

在本节中，由于上述永磁球形电机的转子体采用非导磁材料，以及定子线圈无铁心的设计，使得整个永磁球形电机的转矩模型可以通过单对永磁体线圈的最小转矩模型表示。

首先，在永磁球形电机上，建立单对永磁体线圈的轴线夹角和其转矩的函数关系。通过拟合有限元仿真数据获得单对永磁体线圈的矩角函数关系。然后，根据线性叠加原理，在此函数关系基础上，建立第i定子线圈和第j永磁体的最小转矩模型为

(7)

其中：Ii表示第i定子线圈的电流大小；xsi和xrj∈R3分别表示第i定子线圈和第j永磁体的位置向量；f(Γij)表示第i定子线圈(Ii=1 A)和第j永磁体之间的矩角函数关系，如图4所示；τij表示第i定子线圈和第j永磁体之间产生的转矩。

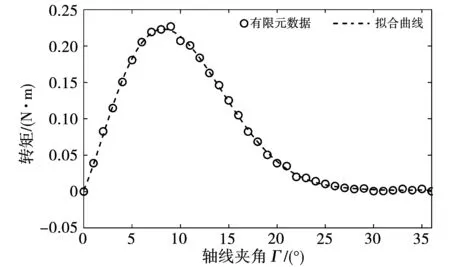
图4 单对永磁体线圈的矩角函数Fig.4 Function of torque and angle between a PM pole and a coil

最后，根据最小转矩模型(7)，便可以得到永磁球形电机的转矩模型为

(8)

将式(8)写成矩阵形式可得

(9)

其中：I∈R24表示24个定子线圈的电流；G∈R3×24表示转矩贡献矩阵，它随着转子位置的变化而变化；τ∈R3表示施加在永磁球形电机转子上的转矩。

由永磁球形电机的转矩模型可知，在控制策略给出控制转矩τ后，依据传感器所提供的转子位置信息[21]，便可以确定40个转子永磁体与24个定子线圈的相对位置关系。进而，确定力矩贡献矩阵G。则24个定子线圈的电流I便可由下式确定：

I=GT(GGT)-1τ。

(10)

考虑到永磁球形电机复杂的电磁关系和转矩建模过程中存在的不确定性。在永磁球形电机的复合干扰中引入一个转矩建模误差τT。

综上所述，复合干扰可以被定义为

(11)

则式(3)中的永磁球形电机的动力学方程可以转化为系统状态方程，即

(12)

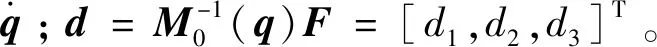
2 自适应干扰观测器的设计

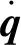
假设2：永磁球形电机的复合干扰和其一阶导数，二阶导数是有界的。

基于永磁球形电机的系统状态方程(12)，对状态变量x2进行如下状态估计：

(13)

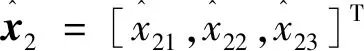
本文采用饱和函数替代符号函数，改进文献[22]的自适应干扰观测器，得到改进后的自适应干扰观测器如下：

(14)

(15)

其中εi>0表示边界层，根据式(12)和式(13)，可以得到

(16)

定义如下的线性滑模函数：

(17)

则由式(14)、式(16)和式(17)可得

(18)

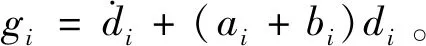
由假设2知，存在一个正常数Li满足

(19)

定义一个Lyapunov函数为

(20)

对时间t求导，可得

(21)

将式(14)和式(18)代入式(21)，根据饱和函数的定义，可得,对于∀|ei|≥εi，

(22)

对时间t积分可得，对于∀|ei|≥εi，

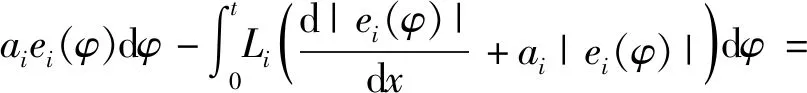
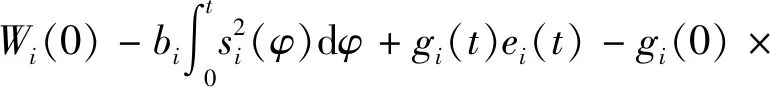
(23)

根据式(19)和式(23)可得，对于∀|ei|≥εi，

Wi(t)≤Wi(0)-gi(0)ei(0)+Li|ei(0)|。

(24)

则,对于∀|ei|≥εi，

|si|≤pi=

(25)

解下面的微分不等式：

(26)

可得，对于∀|ei|≥εi，

(27)

因此，

(28)

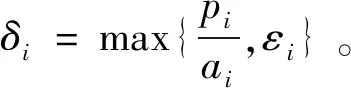
当t→∞时，

|ei|≤δi。

(29)

根据不等式(26)，有

(30)

可得

(31)

因此，当t→∞时，

(32)

3 基于自适应干扰观测器的非奇异终端滑模控制器的设计

本节提出一种基于自适应干扰观测器的连续非奇异终端滑模控制策略，将自适应干扰观测器对复合干扰的观测值在终端滑模控制器的前端进行补偿，图5为本文提出控制算法的系统框图。

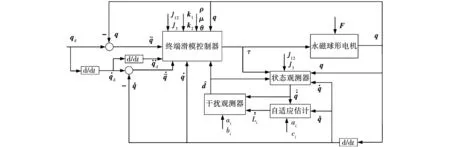
图5 控制系统框图Fig.5 Block diagram of the control system

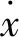
(33)

其中x0表示达到滑模面s=0时的初始状态[22]。

针对永磁球形电机，设计如下的终端滑模函数：

(34)

(35)

永磁球形电机的连续非奇异终端滑模控制律设计如下：

(36)

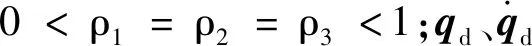
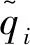
(37)

(38)

(39)

证明：定义一个Lyapunov函数

(40)

对Lyapunov函数求导，得到

(41)

并将式(12)代入，可得

(42)

将控制律(36)代入上式，可得

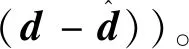
(43)

从而可以得到：

(44)

(45)

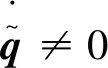
|si|≤Δ1i=(pi+aiδi)/k1i。

(46)

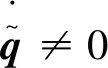
|si|≤Δ2i=((pi+aiδi)/k2i)1/ρi。

(47)

综上所述，滑模函数si渐近收敛到如下有界邻域内：

|si|≤Δi=min{Δ1i,Δ2i}。

(48)

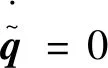
(49)

那么，

(50)

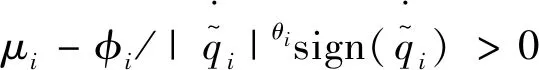
(51)

进而根据式(49)，永磁球形电机的欧拉角位置误差将在有限的时间内收敛到下面的有界邻域内：

(52)

证毕。

4 仿真结果与分析

影响永磁球形电机轨迹跟踪性能的主要因素有外部扰动、摩擦力矩和模型误差。因此，本节从这3个方面进行仿真比较。

设置外部扰动如下形式：

τd1=r1[sint,cost,1]T。

(53)

其中r1表示外部扰动系数。

永磁球形电机的动力学模型误差被设置为

(54)

其中r2表示模型误差系数。

永磁球形电机的转矩模型误差设置为

τT=[0.002,0.002,0.002]T。

(55)

永磁球形电机的3个轴向摩擦力矩，采用库伦+粘滞摩擦力矩模型，形式如下：

(56)

其中：τC表示库伦摩擦力矩；τV表示粘滞摩擦力矩系数。

给定的期望轨迹为

(57)

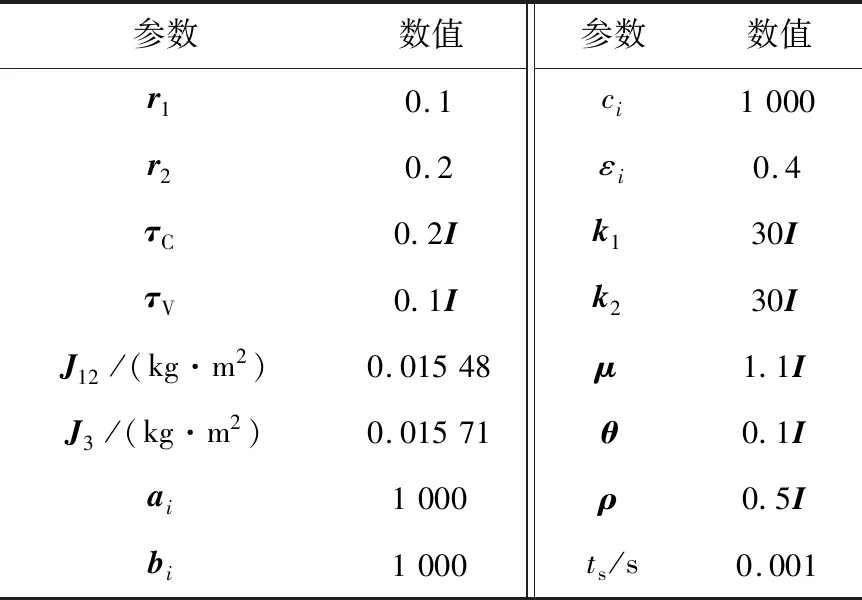
表1 仿真参数Table 1 Simulation parameters

图6为r1=0.1,r2=0.2时，线性滑模控制算法和本文所提出的控制算法的轨迹跟踪误差曲线。从图6可以看出，当系统达到稳态后，用本文所提出的控制算法在跟踪期望欧拉角α、β、γ过程中的稳态误差更小。图7为r1=0.1,r2=0.2时，连续非奇异终端滑模控制算法和本文所提出的控制算法的轨迹跟踪误差曲线。从图7可以看出，本文所提出的控制算法依然保持更小的稳态误差。表2为3种控制算法下，轨迹跟踪误差的均方根值。从表2可以直观地看出，所提出的控制算法具有更小轨迹跟踪误差的均方根值。

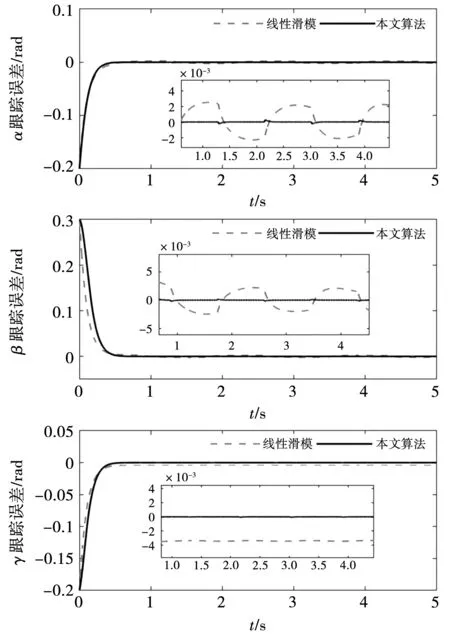
图6 跟踪误差Fig.6 Tracking error

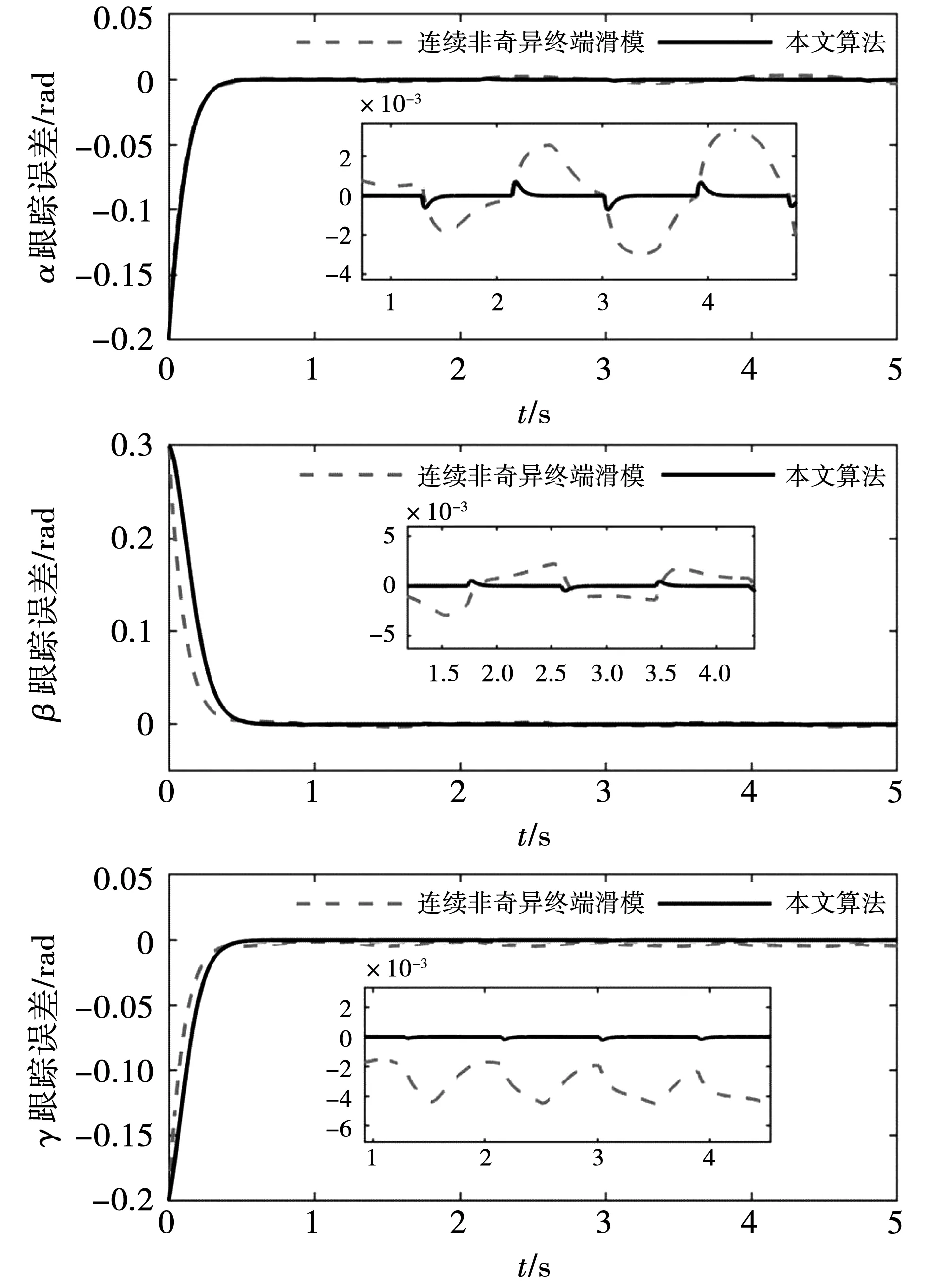
图7 跟踪误差Fig.7 Tracking error

表2 跟踪误差的均方根值(r1=0.1,r2=0.2)Table 2 Root mean square value of tracking error(r1=0.1,r2=0.2)

图8比较了永磁球形电机在线性滑模控制算法和本文所提出的控制算法下的控制转矩。图9比较了永磁球形电机无自适应干扰观测器的连续非奇异终端滑模控制算法和本文所提出的控制算法的控制转矩。从图8和图9可以看出，本文所提出的控制算法与采用边界层的线性滑模控制算法、连续非奇异终端滑模控制算法一样具有连续的控制转矩。但是，所提出的控制算法采用了自适应干扰观测器，使得永磁球形电机在保持高精度轨迹跟踪的性能下，在起动时具有更小的初始控制转矩。

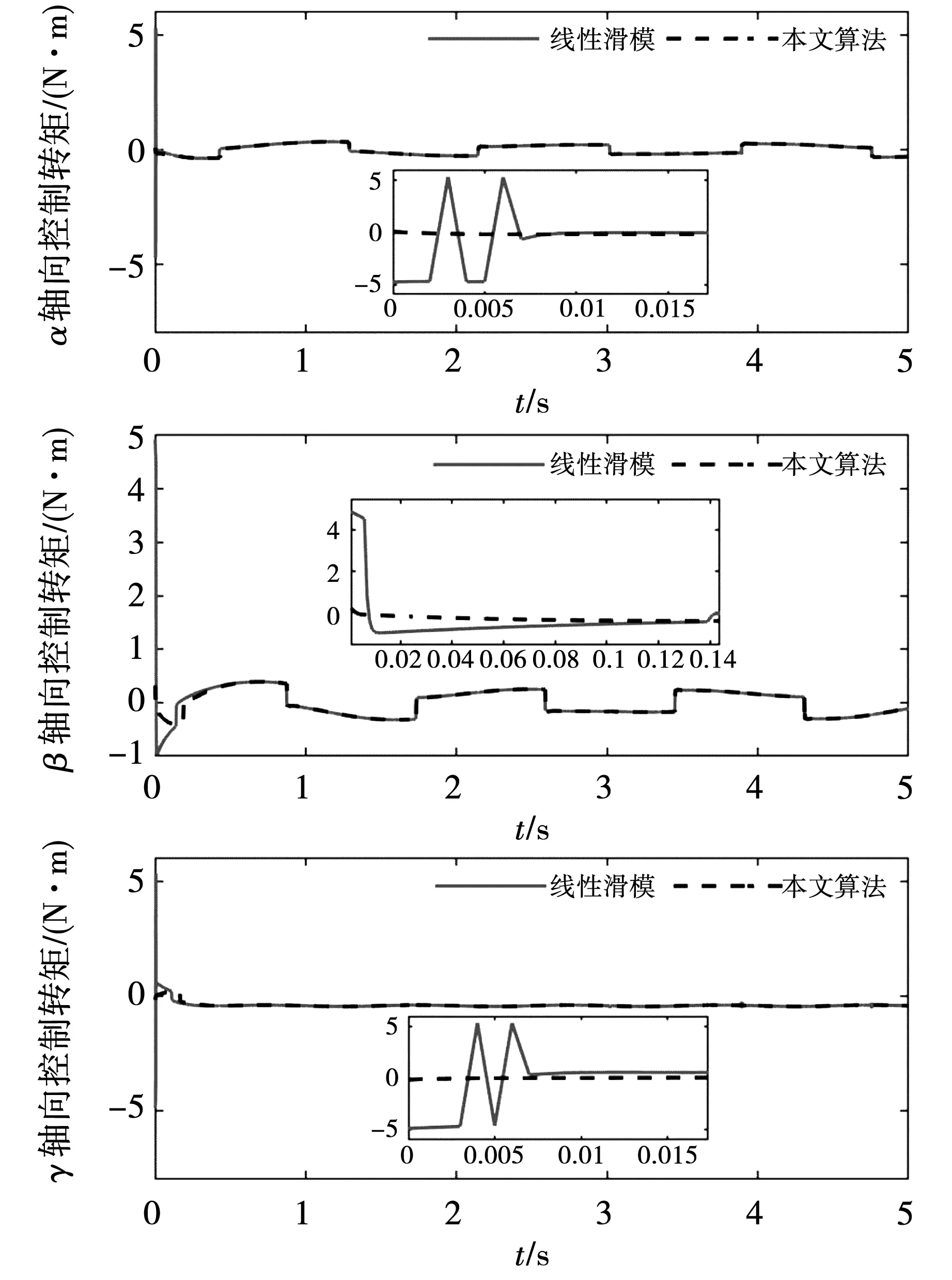
图8 控制转矩Fig.8 Control torque

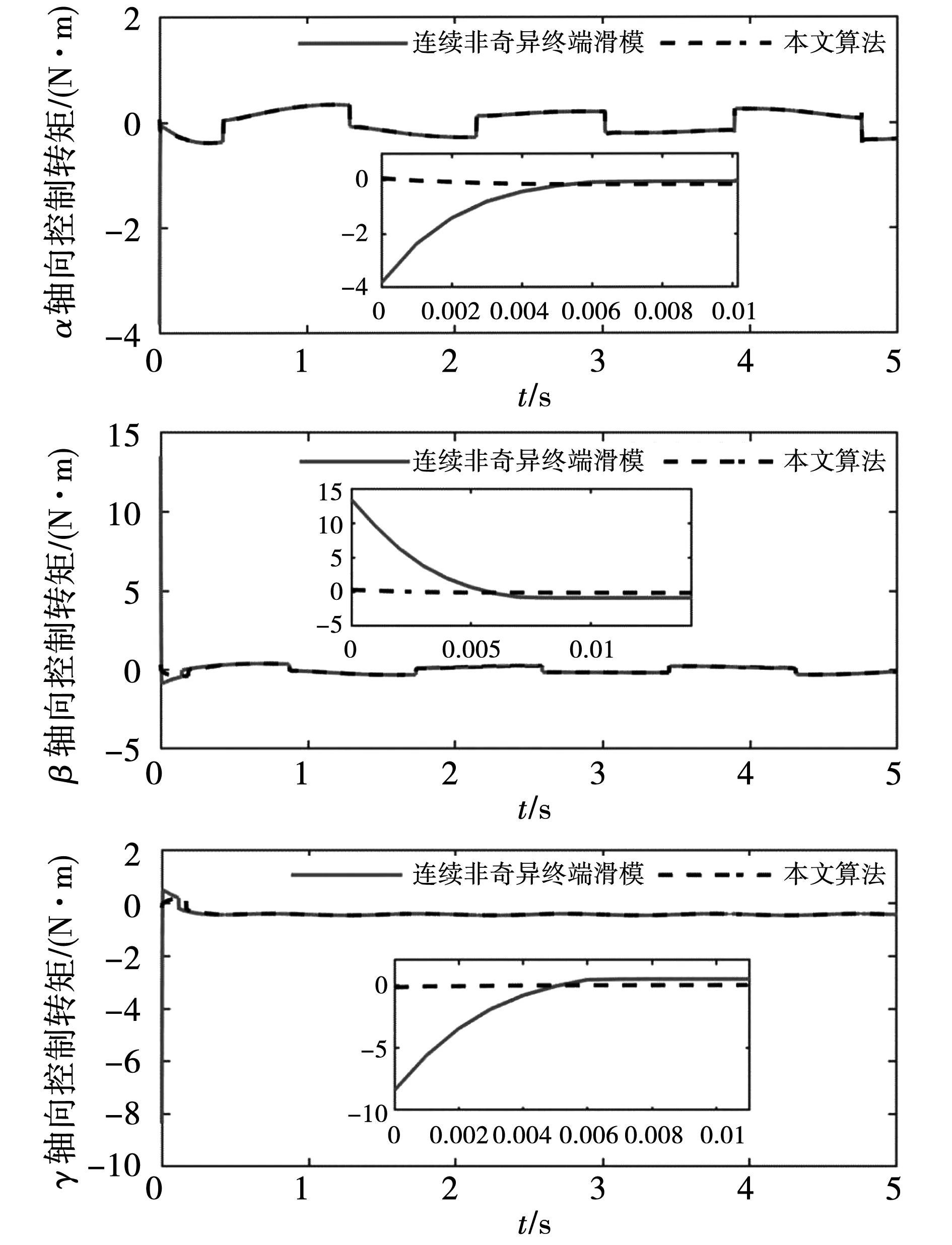
图9 控制转矩Fig.9 Control torque

为了验证所提出控制算法的低灵敏性和强鲁棒性，将外部扰动提高10倍，即r1=1，将永磁球形电机的动力学模型误差从20%提高到50%，即r2=0.5，进行了3种控制算法的仿真比较。表3为3种控制算法的轨迹跟踪误差均方根值。对比表2和表3，可以看出，所提出的控制算法对系统参数和复合扰动变化具有更低的灵敏性和更强的鲁棒性。

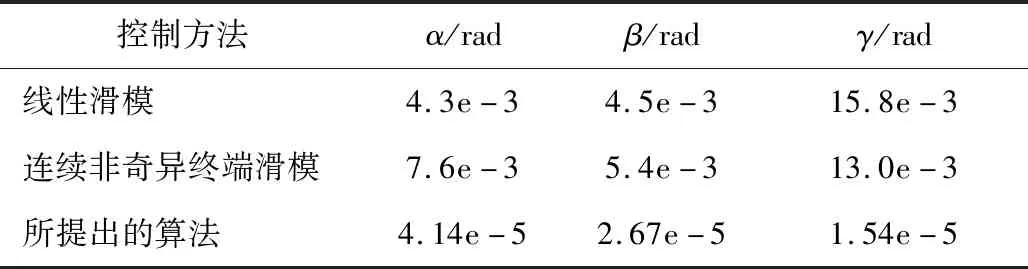
表3 跟踪误差的均方根值(r1=1,r2=0.5)Table 3 Root mean square value of tracking error(r1=1,r2=0.5)

为了验证干扰观测器中自适应率对永磁球形电机轨迹跟踪控制性能的影响，本文进行了有无自适应估计的干扰观测器仿真比较。图10为r1=0.1,r2=0.2时，在无自适应估计的干扰观测器和本文所提出的自适应干扰观测器两种情况下，永磁球形电机在跟踪期望轨迹时所产生的轨迹跟踪误差曲线。从图10可以看出，在相同的连续非奇异终端滑模控制下，运用本文所提出的自适应干扰观测器能够明显降低永磁球形电机轨迹跟踪时欧拉角α、β、γ的跟踪误差。进一步分析可知，相比运用无自适应估计的干扰观测器，本文所提出的控制算法可以使欧拉角α、β、γ的最大轨迹跟踪误差降低30%左右。

图11为自适应干扰观测器在改进前和改进后对永磁球形电机的3个轴向复合干扰的估计。从图中可以看出，改进后的自适应干扰观测器对永磁球形电机的复合干扰具有更好的观测效果。改进前的自适应干扰观测器，在观测永磁球形电机复合干扰时，观测值会产生严重的高频抖振。因此，当改进前的干扰观测值在控制器前端进行补偿时，会使得控制转矩产生同样的振动现象，这会激发永磁球形电机未建模的高频动态，影响永磁球形电机控制系统的稳定性和轨迹跟踪控制的效果，且容易导致永磁球形电机饱和输出，甚至危害控制器和驱动器的寿命。

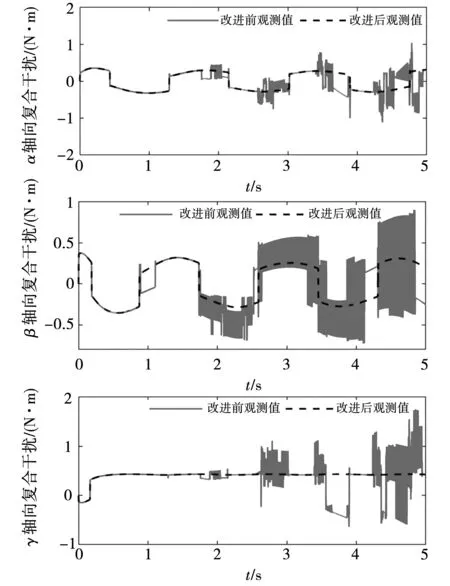
图11 复合干扰及其观测值Fig.11 Lumped disturbance and its observed value

5 实验结果与分析

在本节中，为了验证所提出的控制算法有效性，搭建了永磁球形电机闭环控制系统的实验平台。图12给出了永磁球形电机的滑模控制系统框图。从图12中可以看出，首先，利用滑模控制算法获得理想的控制转矩信号。然后，再根据逆转矩模型，获得永磁球形电机24个定子线圈的电流，从而驱动永磁球形电机按期望轨迹运动。

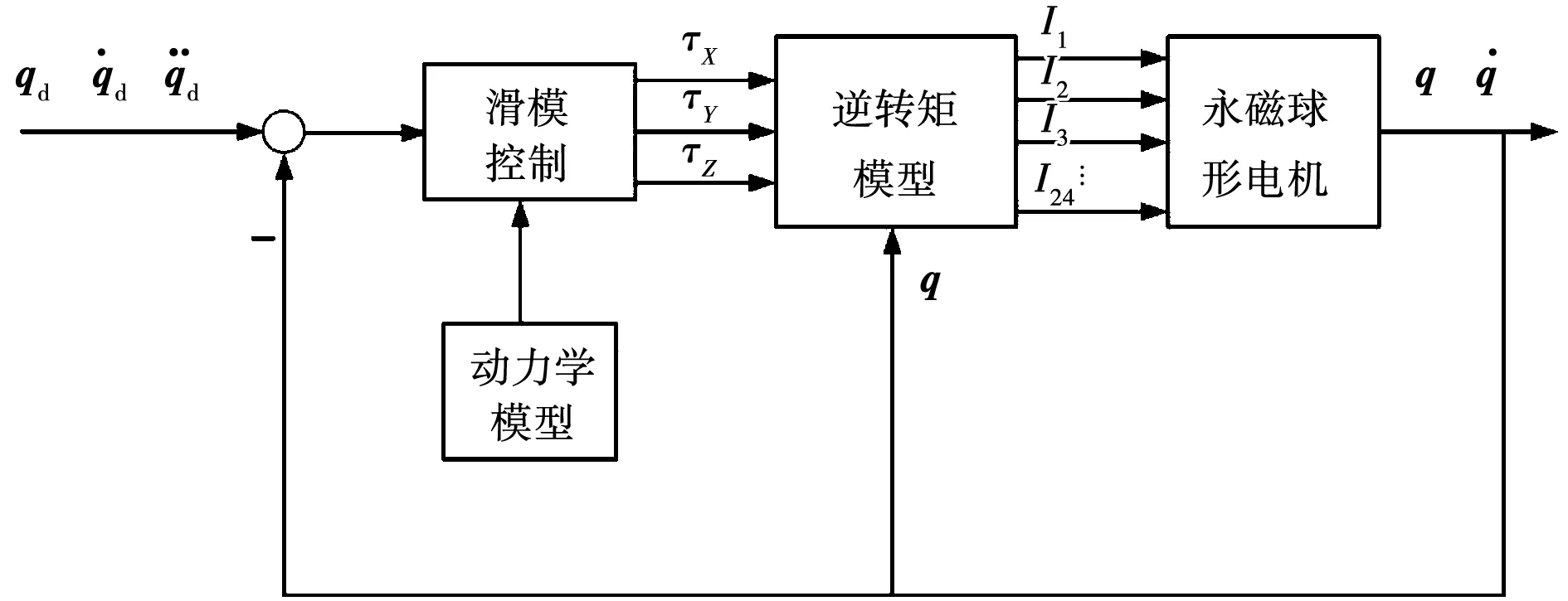
图12 永磁球形电机滑模控制的系统框图Fig.12 System block diagram of sliding-mode control for PMSA

实验平台如图13所示，主要由5个部分组成，分别是作为上位机的计算机、直流电源、电压-电流变换装置、永磁球形电机样机和位置检测传感器MPU6050。图14为永磁球形电机闭环控制系统的实验框图，其中上位机主要进行控制算法的实现，转矩模型的解算,接收永磁球形电机姿态信息以及发送24个定子线圈电流信息给电压-电流变换装置。直流电源主要给电流-电压变换装置供电。电压-电流变换装置主要是根据上位机提供的电流信息来给永磁球形电机的24个线圈提供驱动电流。MPU6050包含了三轴陀螺仪和三轴加速度计，主要检测永磁球形电机转子的位置和速度。

图13 实验平台Fig.13 Experimental platform

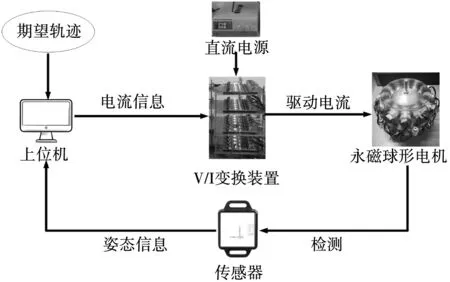
图14 永磁球形电机闭环控制系统的实验框图Fig.14 Experimental block diagram of closed loop control system for PMSA

5.1 倾斜运动实验

为了验证本文算法的有效性，进行了本文所提出的控制算法和线性滑模控制算法的实验比较。设给定的期望轨迹为qd=[20°,20°,0]T，即永磁球形电机的输出轴倾斜到指定点位置。

图15和图16分别为2种控制算法的跟踪轨迹。从图15可以看出，在线性滑模控制下，α和β到达稳态的时间大约为1.76 s和2.05 s。此外，在永磁球形电机到达稳态后，α、β、γ的最大稳态误差分别为2.13°、1.65°和1.70°。而从图16可以看出，在本文所提出的控制算法下，永磁球形电机能够更快地到达稳态,α和β到达稳态的时间大约为0.72 s和1.06 s。且稳态误差更小，α、β、γ的最大稳态误差仅约为0.28°、0.42°和0.21°。

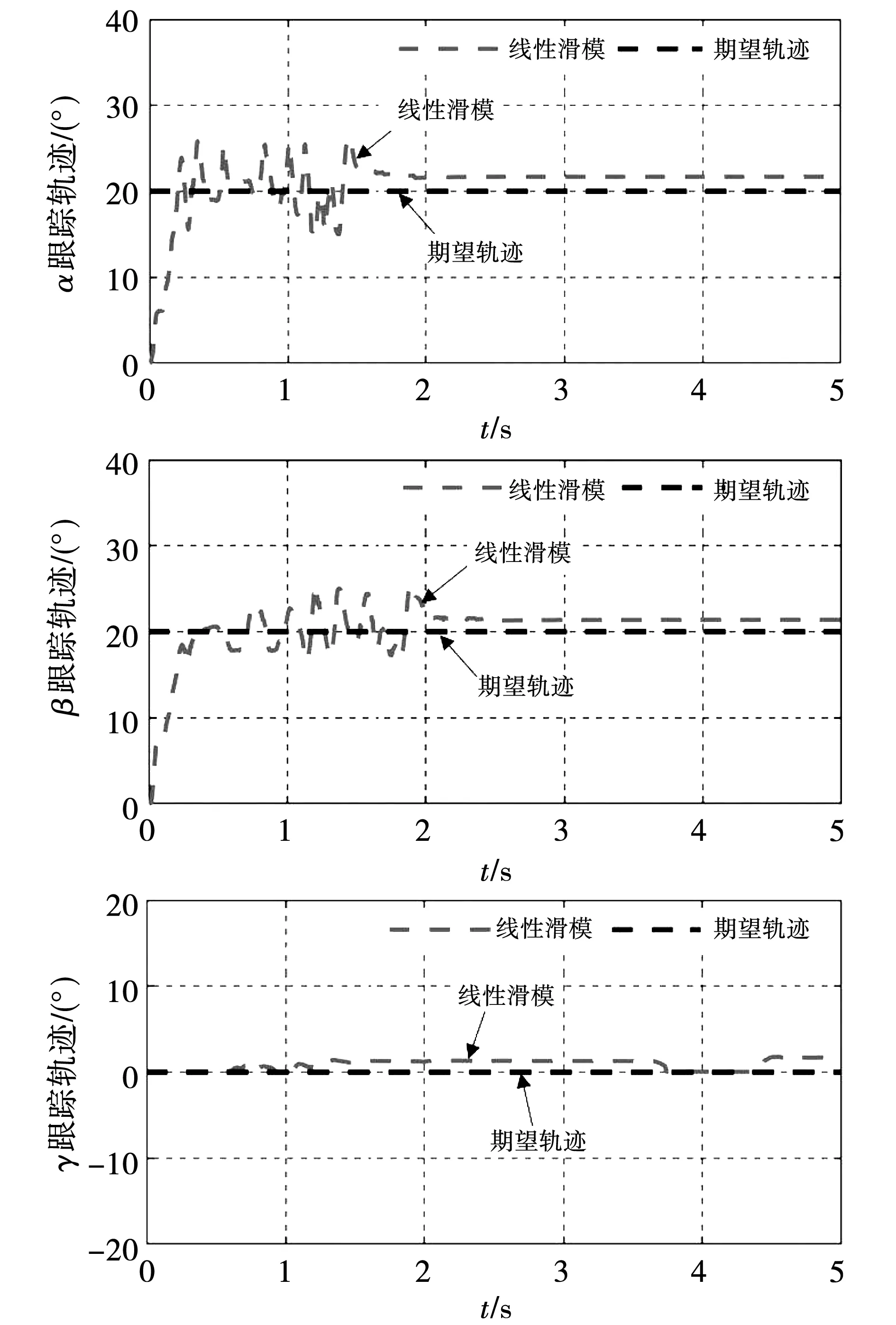
图15 线性滑模控制算法下的轨迹跟踪Fig.15 Trajectory tracking under linear sliding-mode control algorithm

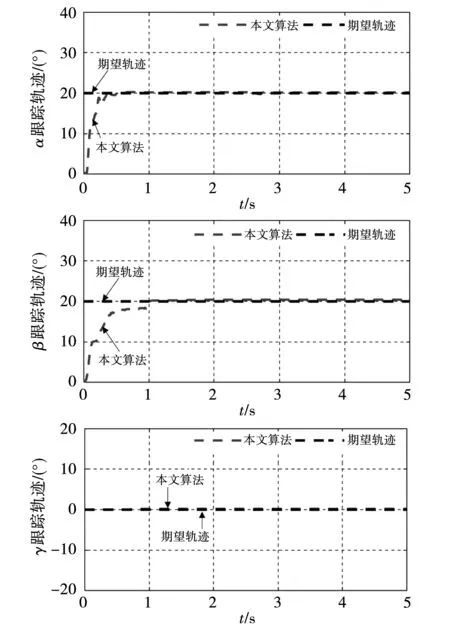
图16 所提出的控制算法下的轨迹跟踪Fig.16 Trajectory tracking under the proposed control algorithm

5.2 自旋运动实验

为了进一步验证本文算法的精确性，本节将期望轨迹设置为qd=[0,0,(36t)°]T，即永磁球形电机的输出轴以恒定角速度做自旋运动。

图17和图18分别展示了线性滑模控制算法和本文所提出的控制算法在进行自旋运动时欧拉角γ的跟踪轨迹。对比图17和图18可以看出，所提出的控制算法更接近给定的期望轨迹。此外，在整个轨迹跟踪过程中，使用线性滑模控制算法的最大跟踪误差为5.84°，而使用所提出的控制算法，其最大跟踪误差仅为2.17°。

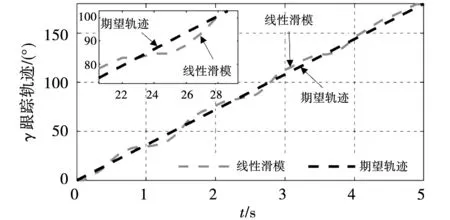
图17 线性滑模控制算法下的轨迹跟踪Fig.17 Trajectory tracking under linear sliding-mode control algorithm

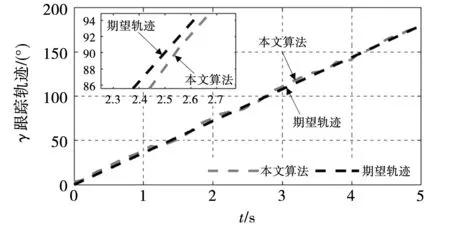
图18 所提出的控制算法下的轨迹跟踪Fig.18 Trajectory tracking under the proposed control algorithm

上述两个实验的结果表明，在实际的永磁球形电机控制系统中，由于信号传递过程中的延时、永磁球形电机的结构并非严格对称而造成的转子振动以及MPU6050传感器的测量精度不够理想等一系列问题的存在，导致了永磁球形电机在本文所提出的算法下仍然具有一定的跟踪误差，特别是进行自旋运动时，由于传感器在Z轴方向具有累计误差，导致其跟踪误差比倾斜运动时更高。但从实验结果不难看出，在摩擦、外部干扰、模型误差等未知复合干扰的影响下，所提出的控制算法相比于传统的线性滑模控制算法，减小了永磁球形电机轨迹跟踪的误差，提高了其轨迹跟踪的精确度。

6 结 论

本文针对永磁球形电机提出了一种基于自适应干扰观测器的连续非奇异终端滑模控制策略，提高了永磁球形电机的轨迹跟踪性能。考虑到永磁球形电机的外部扰动，摩擦力矩和模型误差等在内的复合干扰对永磁球形电机轨迹跟踪控制的影响，提出了一种改进的自适应干扰观测器，实时地估计永磁球形电机的复合干扰。并将复合干扰的观测值在连续非奇异终端滑模控制器的输入端进行补偿。仿真结果表明，在复合干扰下，所提出的控制算法具有连续非奇异的控制转矩，并且比传统线性滑模控制和连续非奇异终端滑模控制具有更小的轨迹跟踪误差和初始控制转矩。实验结果表明，在轨迹跟踪过程中，所提出的控制算法使得永磁球形电机更快地到达稳态，并且比线传统性滑模控制具有更小的跟踪误差。综上所述，后续可以考虑从以下两个方向进行改进来改善永磁球形电机的轨迹跟踪效果：

1)可以考虑利用延时观测器来处理实际永磁球形电机控制系统的时滞现象。

2)可以考虑利用速度观测器来实时估计永磁球形电机的角速度，从而避免传感器信号的延迟。