缺资料地区降雨量空间插值方法比较

李治军，王华凡，侯 岳，黄佳俊

(1.黑龙江大学 水利电力学院，黑龙江 哈尔滨 150080;2.黑龙江大学寒区地下水研究所，黑龙江 哈尔滨 150080)

降雨量数据是进行产汇流计算的重要基础，是进行地区水文循环规律研究、水资源供需平衡分析和旱涝灾害预警机制建设的重要支撑[1-2]。我国幅员辽阔，气候条件复杂多样，水文气象观测站点少且分布不均，存在许多县区仅拥有一个水文气象观测站点的现象。

本文以无资料流域水文预报(PUB)计划为切入点，探讨适用于缺资料地区降雨量求算的空间插值方法，以位于黑龙江省同江县等9个偏远县区的9个气象观测站点2000—2014年的降雨量数据为基础，在考虑高程和样本点间距离等影响因素的情况下，采用反距离权重法(IDW)，薄板样条函数插值法(Splines)，全局多项式插值法(GPI)，局部多项式插值法(LPI)，普通克里金插值法(OK)和协同克里金插值法(CK)，借助地理信息系统(GIS)的地理空间分析工具，对研究区进行年降雨量、各年7月降雨量及次降雨量的空间插值计算，经交叉验证分析，优选出针对不同降雨量大小的精确度最高的空间插值方法，为缺资料地区降雨量空间插值提供理论指导，为产汇流计算研究提供降雨量数据获取的方法参考。

1 研究方法

1.1 分类

空间插值是根据已有的一定数量的反映空间某种要素分布特征的样本，对未知空间进行预测的一种算法。按照推求的空间范围，可分为内插和外推。空间内插通过已知点数据推求同一区域未知点的数据，而空间外推则通过已知区域的数据推求同域外未知点的数据。按照插值结果实现的数学原理，可分为确定性插值法和地统计插值法(又称克里金插值)，确定性插值法以研究区内部相似程度或平滑度为基础，由已知样本点创建插值表面。地统计插值法在量化样本点之间的空间自相关的基础上，利用频率分布、方差和均值等统计特性，进一步解释说明了采样点在预测区域的空间分布情况[3-5]。张莉莉等基于海南岛18个观测站点的气象数据，应用GIS中的插值工具，通过交叉验证，对比分析，得出混合插值法最优于海南岛气象要素空间插值的结论[6]。蒋育昊等考虑高程、坡向和距离等影响降雨量大小的因素，利用PRISM模型对北京西北山区的月降雨量进行插值分析，论证了在复杂地形条件下PRISM插值方法相对于其他方法，能够更加准确地描述降雨的空间分布[7]。陈雅婷和刘奥博以中国1915个气象站30年的平均降水量为数据基础，利用经验贝叶斯克里金法、泛克里金法和多项式法等插值方法进行全国范围内的降雨量插值精度分析，经误差分析验证，结果表明，通过估计基础半变异函数来表示数据误差的经验贝叶斯克里金法插值效果最好，输出表面最为光滑[8]。降雨量空间插值方法众多，不同方法得出的插值输出表面效果差异较大，输入数据聚类情况、样本点数量和研究区地形地貌类别等因素都直接影响插值的精度。本文对上述各类插值方法的特点进行归纳，有助于进一步决策选取何种方法进行插值计算，见表1。

表1 常用插值方法特点归纳

1.2 插值方法

反距离权重插值法(IDW)基于相近相似的地理学原理，利用样本点被赋予的不同权重，进行插值计算。该法假定插值表面特性取决于局部变化，如采样点均匀分布，不存在聚类现象，则插值效果最佳。

薄板样条函数插值法(Splines)基于使经过所有样本点的预测表面达到最小曲率的思想，进行插值点的数据预测。该法要求采样点数据准确，预测表面在短距离内各点数据值不能相差太大。

全局多项式插值法(GPI)依据多项式拟合的一个插值表面，形成具有数值分布的采样区，结合最小二乘法原理，利用采样区地理坐标(x,y)，推求降雨量z的数值，以此进行数据拟合并估计待测点值。该法计算简便，结果精度较低。

局部多项式插值法(LPI )使用位于指定重叠领域的多个多项式进行插值表面拟合，对具有多种形状的拟合表面，多个多项式的拟合效果会明显优于单个多项式。

普通克里金插值法(Ordinary Kriging)基于变量的空间相关性，依赖于克里金法的将感兴趣变量空间自相关作为距离的函数，利用样本点的原始数据与变异函数的结构特点，对待插点进行无偏，最优化估计。该法要求观测数据服从正态分布，参数较多，确定最佳参数形成最佳插值表面相对复杂。

协同克里金插值法(Co-Kriging)将区域化变量从单一属性发展至两个及以上的协同属性，可在降雨预测模拟中纳入风向和地形等影响因子，进一步认识降雨的潜在空间特征，提高降雨插值精度，引入高程影响因素的协同克里金插值法。

1.3 交叉验证

交叉验证将样本点分为训练集和验证集，使用训练集做插值分析，利用验证集测试插值效果，通过比较预测值与观测值的误差，进而评估插值结果和方法的优劣。本文采用交叉验证方法中的平均误差、均方根误差和标准化均方根误差综合优选不同雨量条件下的插值方法。

2 应用实例

2.1 研究区概况

本文的研究区位于黑龙江省东北部的三江平原，选取位于集贤县、宝清县、绥滨县、同江市、富锦市、双鸭山市、饶河县、密山市和虎林市的9个气象站点。

根据实测的气象站点的降雨量数据，在整个考察年份内，9个气象站点记录的多年平均年降雨量值大多在500.0 mm左右，最大值位于虎林市，为610.8 mm，最小值位于富锦市，为488.3 mm。

为进一步考察各气象站点记录的降雨量年内分布情况，对考察年份内的月降雨量进行统计分析，结果表明，年内降雨多集中在7月和8月，其中7月份的多年平均月降雨量年内占比最大，9个气象站点均超过20.00%，最大值为宝清县的25.75%。

2.2 样本点相关性分析

空间插值分析主要包括获取原始数据、分析数据、选择合适的预测模型和验证插值结果的合理性，其中分析数据部分包括检验数据是否服从正态分布、全局趋势性分析和各向异性分析等。本文运用ArcGIS软件地理统计分析模块对各气象站点的年降雨量、各年7月降雨量及选取的场次降雨量数据进行相关性分析，利用QQ plot 分布图检验数据的正态分布情况，验证是否存在离群值，利用全局趋势分析，对数据的趋势效应进行分析。通过对各站点年、月和场次降雨量进行正态分布及趋势分布检验。分析结果表明，除部分站点某年或某月降雨量值存在离群点，其他数据均具有良好的正态分布和趋势分布效果。本文立意于缺资料地区降雨量插值计算研究，样本数据较为稀缺，且各站点数据均为气象台站观测所得，故在插值处理时不剔除离群点和引起趋势变化较大的点，节选的样本点不同雨量下的趋势分布和正态分见图1～图3。

图1 年降雨量

图2 月降雨量

图3 场次降雨量

3 插值结果分析

通过ArcGIS软件中的地理统计分析工具，运用上文提到的各种插值方法，对研究区的降雨数据进行插值分析，经交叉验证，并对结果进行转换分析，得到各种方法在不同雨量情况下的误差情况，具体结果见表2。

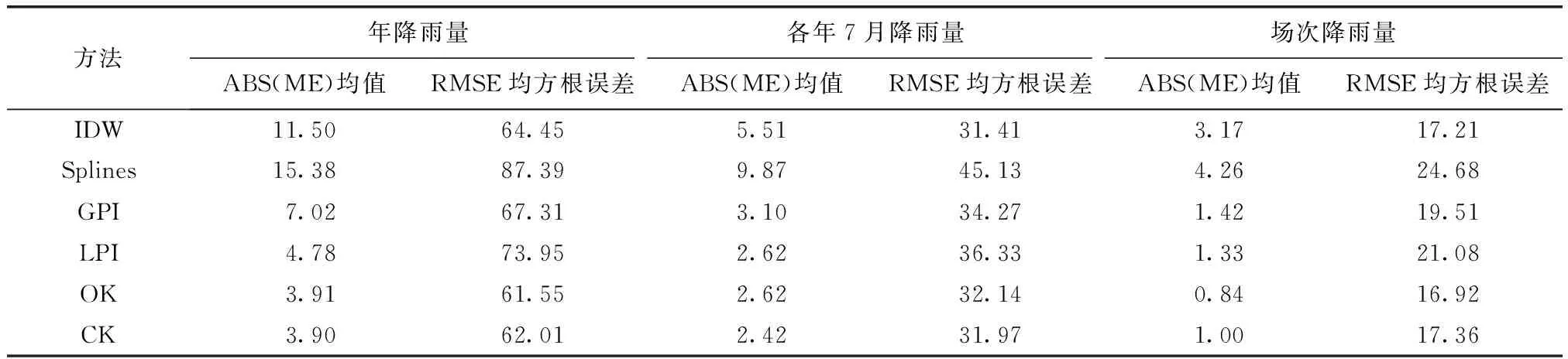
表2 不同雨量情况下插值方法误差结果 mm

由表2可知，在数值较大的年降雨量插值模拟中，OK法和CK法得出的插值误差结果优于其他方法。为进一步优选出各雨量情况下最好的插值方法，对OK法和CK法的插值结果进行均方根误差标准化的计算，进一步预测标准误差的有效性，经计算，OK法的结果为0.95，CK法的结果为1.17，参照数值结果与1越近效果越好的判断标准，可得出OK法最适合缺资料地区年降雨量的空间插值计算。在数值大小居中的各年7月降雨量插值模拟中，CK法得出的插值误差结果优于其他插值方法，在样本点数据较少并结合研究区高程数据的情况下，该法可充分考虑地形地貌对降雨量数据的影响，避免了插值时同一组样本数据过于分散造成插值误差较大的结果。在数值较小的场次降雨量插值模拟中，OK法得出的插值结果优于其他插值方法。本文采用考察期内各气象站点每年夏季第一场连续三天的降雨数值为样本，雨量值集中分布在50 mm以下，各气象站点数值差较小，OK法在场次降雨量的插值计算中，相对于确定性插值方法，该法利用样本点拟合的线性方程来推求未知点的降雨量数值时，加权值不仅考虑了观测点与未知点的距离，同时考虑了位置和空间结构关系，拟合精度更高，插值误差更小。

4 结 论

(1) 在充分考虑研究区地形地貌和样本点数据空间自相关的情况下，普通克里金法和协同克里金法的插值结果明显优于其他方法，误差较小，插值结果图更加平滑美观。

(2) 在年降雨量插值模拟分析中，降雨量大小呈现由研究区东南向西北递减的趋势；在各年七月和场次降雨量插值模拟分析中，降雨量大小呈现由东北向西南递减的趋势。由此可见，同一研究区域在不同降雨量情况下的插值结果有很大区别，地形地貌及气候条件对地区降雨量大小的影响较大。

(3) 因插值样本点较少，反距离权重法得出的插值结果表面具有明显的“牛眼”现象，观测点数据对全局性的插值结果影响较大，多项式法和薄板样条插值法得出的插值结果表面分层现象严重，平滑度较低，普通克里金法和协同克里金法得出的插值结果表面存在个别图像存在较小范围内的“牛眼”和分层现象，但全局平滑性整体优于确定性插值方法得出的插值表面。

(4) 本文因插值样本点较少，故无法考虑不同样本点情况下的各种插值方法的优劣，随着降雨量空间插值分析的不断深入，多尺度和多要素地对降雨量影响因子分析的愈加全面，缺资料地区降雨量空间插值计算结果将更加精确。