波形钢腹板UHPC组合梁开孔波折板连接件有限元分析

刘志

（湖北交投十巫高速公路有限公司，湖北 十堰 442000）

0 引言

在波形钢腹板组合梁中，连接件是保证混凝土与钢材共同受力的关键。目前已有文献针对开孔波折板连接件展开了破坏机理、承载力及滑移特性的研究[1-2]，但是，在国内外很少采用超高性能混凝土（Ultra-High Performance Concrete,UHPC）作为此类连接件的灌注材料，对连接件的各部分的抗剪贡献研究较少。本文通过ABAQUS模拟推出试验，得到该类型的连接件的荷载—滑移曲线及其破坏形态，研究波高、波角、波长、开孔位置对连接件承载力的影响，并分析混凝土榫、贯穿钢筋和键齿各组成部分的抗剪贡献。

1 有限元模型的建立

目前，探讨连接件抗剪性能的主要试验方法有推出试验和梁试验，Slutter等通过研究得出推出试验结果是梁式试验结果下限的结论[3]，认为将推出试验结果应用于组合梁设计将更加安全。其基本操作过程是，将焊接在工字钢上的连接件嵌入混凝土立方体中，然后对工字钢进行单向加载，使连接件能够承受剪切荷载。为简化计算，根据对称性，可取半模型进行计算。

推出试件尺寸如图1所示。

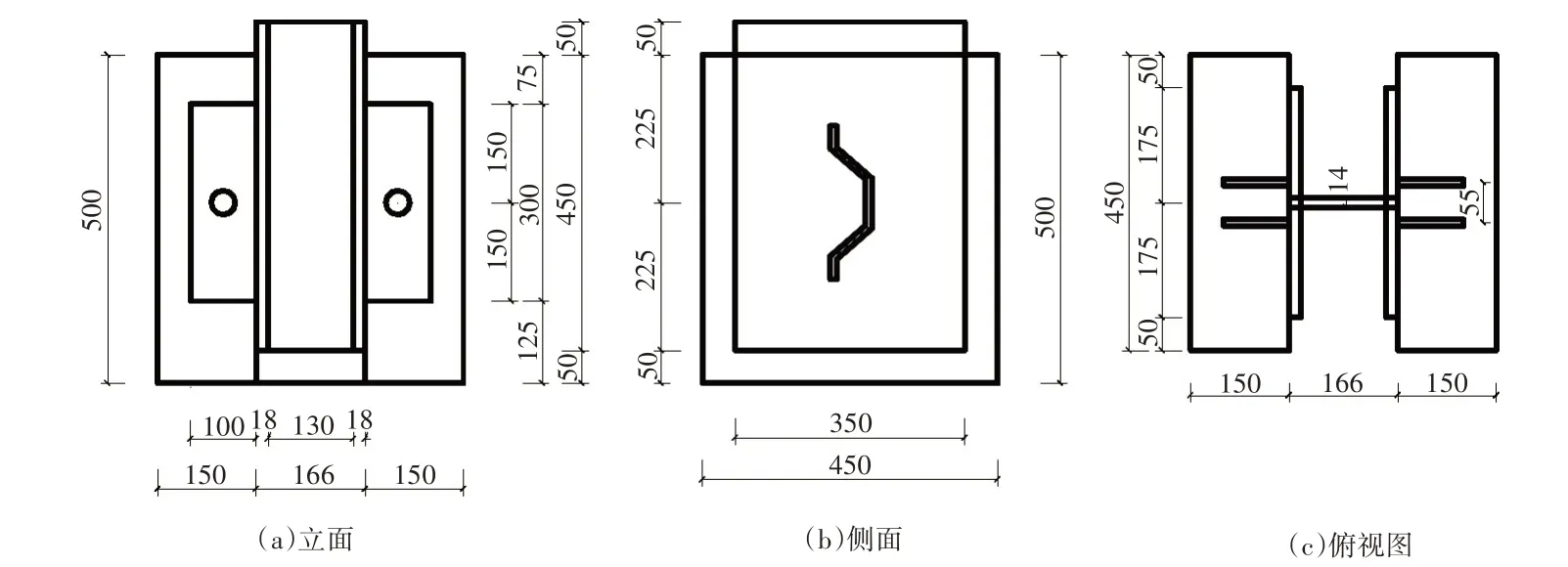
图1 推出试件示意图（单位：mm）

1.1 材料本构关系

（1）UHPC材料参数

弹 性 模 量 取42.6GPa[4]，泊 松 比 为0.2，采 用ABAQUS中的混凝土损伤塑性（Concrete Damage Plasticity,CDP）模型来模拟UHPC的受力，相关参数均按照ABAQUS推荐取值[5]：膨胀角为36°，偏心率为0.1，fcb/fb0取1.16，K取0.666 7，黏性系数取0。

UHPC的受拉应力—应变关系采用张哲等人[6]提出的公式：

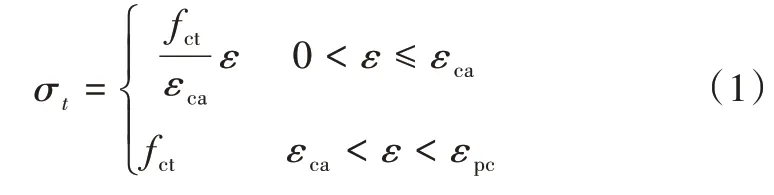
式（1）中：fct为应变硬化阶段平均应力；εca为弹性阶段峰值应变；εpc为极限应变。

本文中：fct=8.0MPa，εca=2×10-4，εpc=1.941×10-3。

UHPC的受压应力-应变关系采用杨剑[7]提出的公式：

式（2）中：fc为圆柱体抗压强度；n=Ec/Es；Ec为初始弹性模量；Es为峰值点的割线模量；ε0=3.5×10-3,ξ=ε/ε0。

研究表明，UHPC圆柱体抗压强度与立方体抗压强度之间的换算系数约为0.95[8]，故取fc=0.95fcu=127.5MPa。由式（1）、式（2）可得UHPC本构关系，如图2所示。

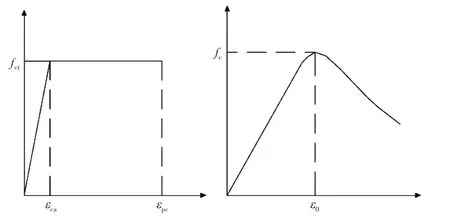
图2 UHPC本构关系曲线

（2）钢材材料参数

贯穿钢筋采用HRB400钢筋，钢板采用Q345钢材。大量的试验研究表明，工字钢在推出试验中处于弹性状态，为了便于计算，本文采用理想弹塑性来表征工字钢和钢筋的本构。其中，钢筋弹性模量为2×105MPa，屈服强度为400MPa；钢板弹性模量为2.06×105MPa，屈服强度为345MPa；泊松比为0.3。

1.2 单元类型的选取

由于贯穿钢筋在抗剪过程中承受弯拉作用[9]，因此贯穿钢筋采用实体单元模拟。钢板、混凝土和贯穿钢筋采用8节点缩减积分的三维实体单元（C3D8R）模拟，箍筋采用两节点线性三维桁架单元（T3D2）模拟。通过ABAQUS自带的“内置区域”，将钢筋单元整体嵌入混凝土主单元中，不考虑主从单元间的相对滑移，而通过计算主从单元节点间的相对位移及转动，有效避免了接触界面模拟所需要的大量且耗时的迭代过程，大幅简化了计算分析。

1.3 钢与UHPC的相互作用

根据李嘉[10]的研究，在推出试验中，钢与UHPC之间的黏结作用对抗剪的贡献约为100kN，考虑到加载至破坏时，黏结作用已失效，故在本文计算时忽略二者之间的黏结作用，钢与UHPC界面的摩擦系数取0.4[11]

1.4 边界条件

约束混凝土下表面x,y,z方向的平动自由度，在工字钢腹板中间施加x方向的对称约束。

2 受力过程分析

在有限元数值计算模型中，通过提取UHPC结构层与工字钢间界面相对滑移以及混凝土底面所有节点的竖向反力之和可以得到剪力连接件的荷载—滑移曲线，如图3所示，该曲线反映了开孔波折板连接件的抗剪性能及受力形态。

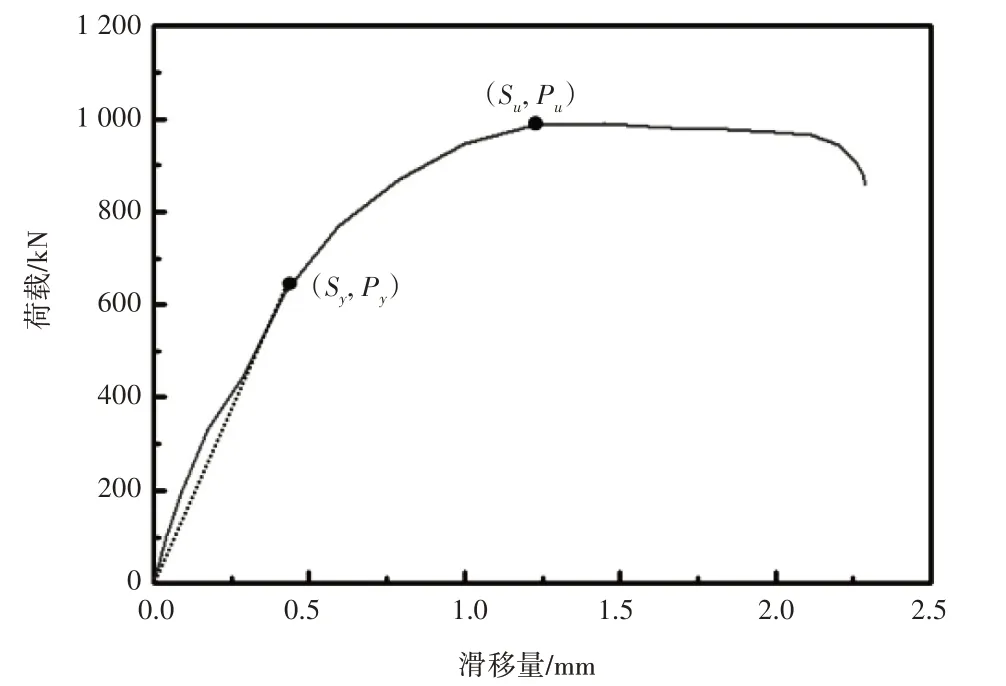
图3 荷载—滑移曲线

在加载初期，工字钢和混凝土的滑移较小（在0.4mm左右），荷载—滑移曲线基本呈一条直线，将此阶段定义为弹性阶段，荷载定义为屈服承载力Py（为0.6Pu左右），Py所对应的滑移量为Sy，抗剪刚度K=Py/Sy；此后，曲线斜率开始缓慢变小，呈现出明显的非线性，剪力连接件的抗剪刚度大幅退化，将此阶段定义为塑性发展阶段，荷载定义为极限承载力Pu，对应的滑移为极限滑移量Su；当荷载达到极限值后，稳定一小段后，滑移量不断增大，荷载开始减小，将此阶段定义为下降阶段。

3 影响因素分析

考虑到目前针对PBL连接件的参数研究已经比较完善，因此本节将针对开孔波折板连接件一些特殊的主要参数进行分析。与普通的PBL连接件不同的影响因素主要有波高、波角、波长以及开孔位置等，具体参数见图4、表1。各影响因素的荷载—滑移曲线如图5~图8所示。

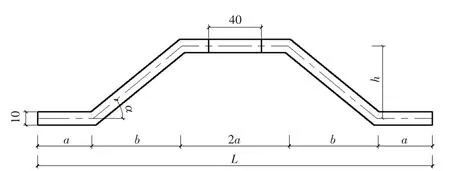
图4 开孔波折板参数示意图（单位：mm）

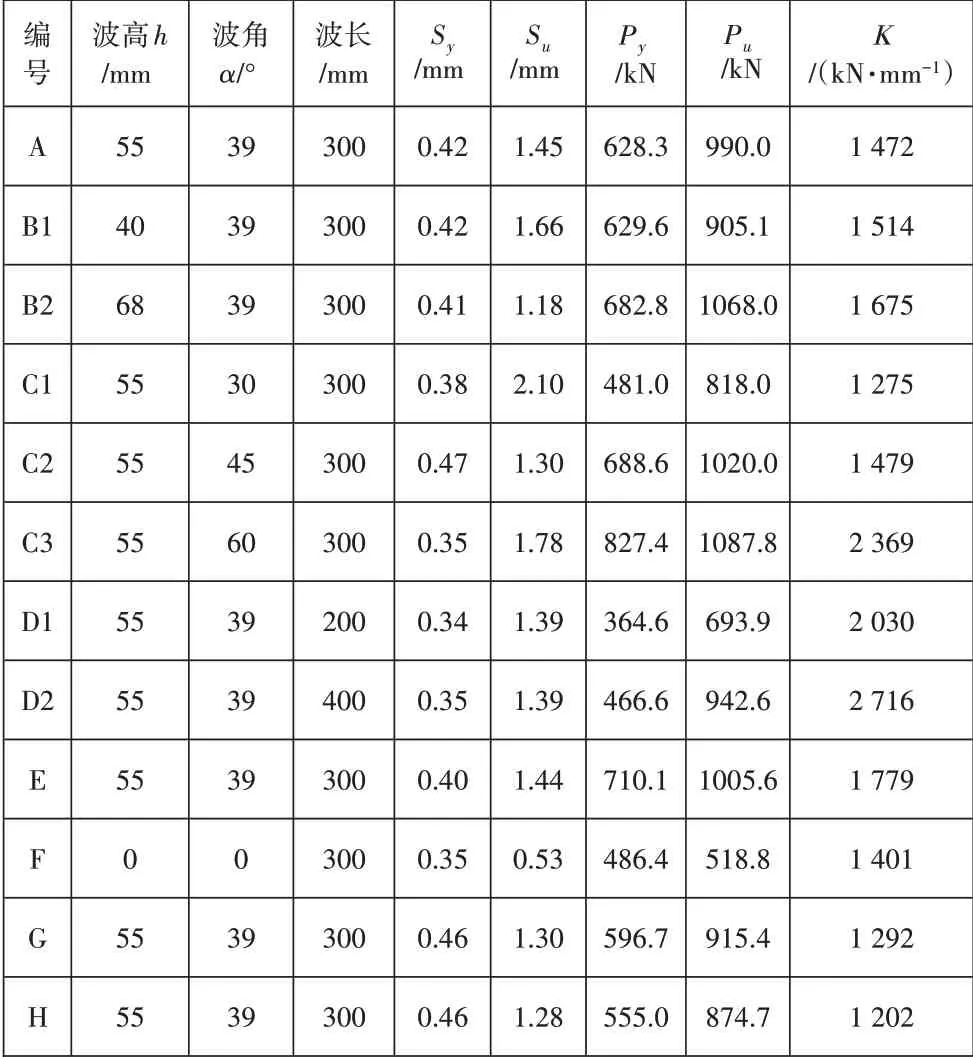
表1 开孔波折板参数分析结果

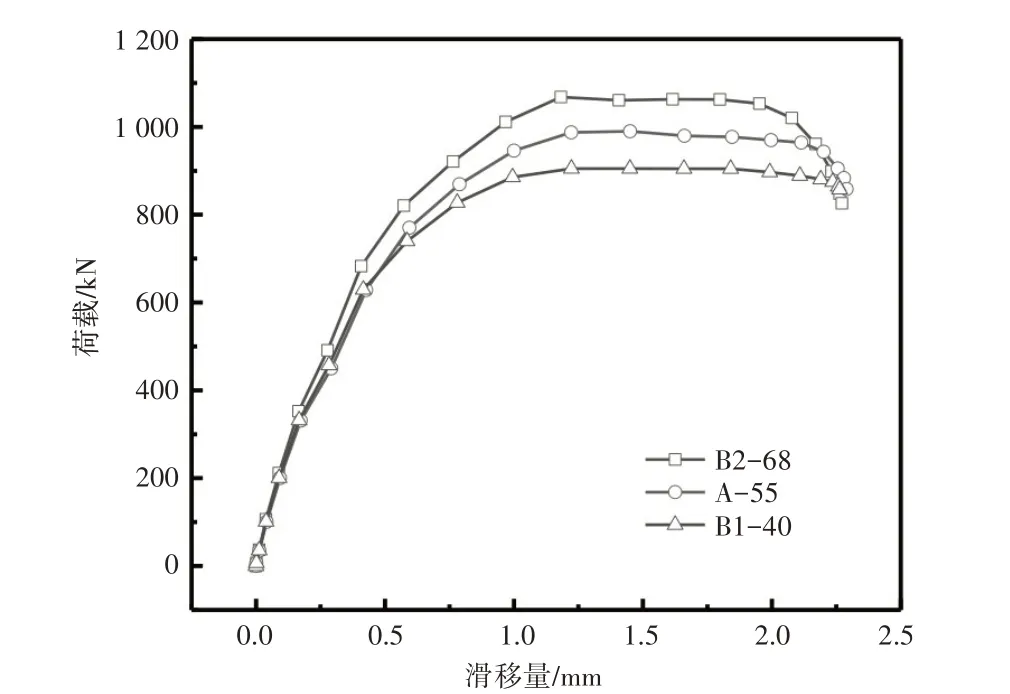
图5 波高的影响

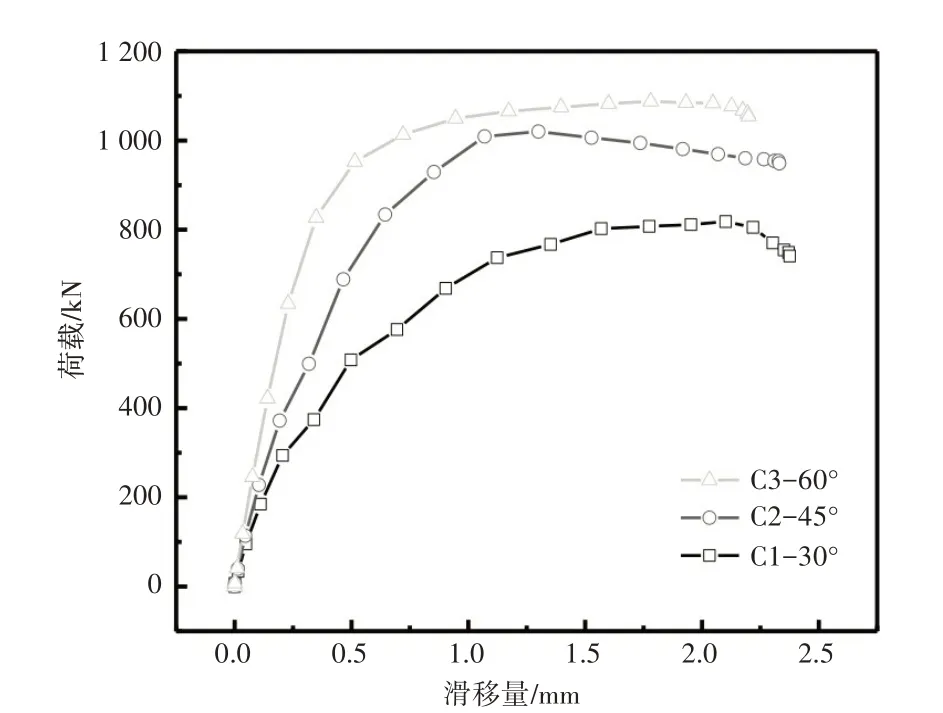
图6 波角的影响

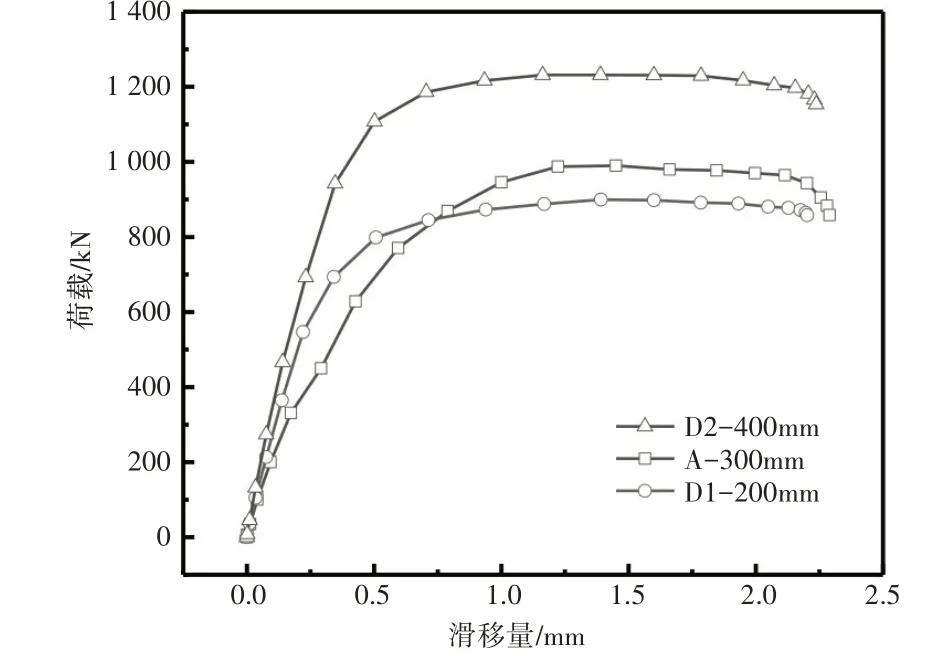
图7 波长的影响

图8 开孔位置的影响

由图5~图7可知：波高对抗剪刚度的影响不大，但极限承载力随着波高的增加而增大；增大波角可以显著提高抗剪刚度，且极限承载力随之增大；这3个模型的斜板的投影面积相同，证明斜板的投影面积并不影响连接件的抗剪能力；增加波折板的波长可以增加极限承载力，波长越长，直板长度越长，由斜折板受压传递给直板的压力扩散得越均匀，因此抗剪能力越强。

由表1和图8可知，斜板开孔的极限荷载为990.0kN，直板开孔的极限荷载为1 005.6kN，看似斜板开孔承载力更高，实际上，在斜板开孔的方案中有两个贯穿孔，而直板开孔只有一个贯穿孔，如果折算为有效抗剪长度，则直板开孔承载力高于斜板开孔方案。

4 受力机理分析

由图9可知，在弹性阶段，三者的荷载—滑移曲线基本重合，说明在线性阶段，贯穿钢筋基本不承受剪力，混凝土键齿承担了绝大部分的剪力；在塑性发展阶段，混凝土榫抗剪比例逐渐增大；在达到极限承载力之后，由于波折板开孔并贯穿钢筋，波折板相对于无孔波折板表现出更好的延性。

图9 开孔与贯穿钢筋的影响

由图10可知，开孔波折板连接件相对于PBL连接件具有更优越的抗剪性能，其抗剪承载力约是同等条件下PBL的1.9倍。

图10 与PBL的对比

5 结论

（1）开孔波折板连接件的荷载—滑移曲线可大致分为3个阶段：弹性阶段、塑性发展阶段和下降段；弹性阶段的滑移量基本在0.4mm左右，屈服承载力大约是极限承载力的60%。

（2）开孔波折板抗剪能力的影响因素主要有波高、波角、波长。波高对抗剪刚度影响较小，增加波高可提高极限承载力；增大波角可以显著提高抗剪刚度，且极限承载力随之增大；波长越长，则极限承载力越大。

（3）斜板开孔受力不合理，承载力低于直板开孔，开孔位置宜选择在直板上，受力更合理且抗剪能力更强。由于斜板承受较大的压力，因此，建议在斜板附近增加箍筋，以改善斜板下方的混凝土受力。

（4）开孔波折板连接件抗剪机理为：在弹性阶段，主要由混凝土齿键承担剪力；在塑性发展阶段，贯穿钢筋可提高极限承载力并增加延性。

（5）同等条件下，开孔波折板连接件的极限承载力约为PBL连接件的1.9倍。