基于Fano 共振的金属-绝缘体-金属-石墨烯纳米管混合结构动态可调折射率传感器*

祁云平 贾迎君 张婷 丁京徽 尉净雯 王向贤

1) (西北师范大学物理与电子工程学院,兰州 730070)

2) (四川大学电子信息学院,成都 610041)

3) (兰州理工大学理学院,兰州 730050)

为了解决传统金属-绝缘体-金属(metal-insulator-metal,MIM)波导结构传感器不可动态调控的问题,本文将石墨烯纳米管引入MIM 波导耦合圆环谐振腔结构,设计了一种动态可调的MIM-石墨烯纳米管混合结构折射率传感器.采用有限元法对系统的传输特性、电场分布和磁场分布进行数值研究,并通过多模干涉耦合模理论进行分析验证.结果表明,Fano 共振源自于TM10 腔共振模式和石墨烯等离子体电共振模式之间的相干耦合.通过改变石墨烯的化学势可以在较大波长范围内动态调谐Fano 共振的谐振波长和线宽,从而实现折射率传感器的动态调控.在最佳结构参数下,传感器灵敏度可达1250 nm/RIU.与传统的MIM 波导结构相比,该器件具有结构简单、动态可调、易于加工且工作波段范围大等诸多优点,对设计可动态调控的高性能纳米光子集成器件具有一定的指导意义.

1 引言

近年来,现代光学器件不断趋向于高度集成化和小型化,这一趋势的发展瓶颈是亚波长结构光学器件无法突破衍射极限[1].表面等离子体激元 (surface plasmon polaritons,SPPs) 是由光子与金属表面的自由电子相互作用所形成的一种高度局域化的倏逝波[2].SPPs 能突破衍射极限且在深亚波长尺寸范围内具有强局域性,由此可以设计出众多高度集成化且小型化的亚波长光学器件[3,4].此外,SPPs 激发出的不同等离激元模式会相互耦合、杂化和干涉,从而产生不同的现象和效应.其中,Fano 共振就是一种典型的源于不同等离激元模式连续态和离散态之间的相干耦合效应,其在光谱中表现为尖锐且不对称的线型,即是由一种连续态和一种离散态的振幅干涉形成[5-7].Fano 共振首次被发现并验证是在原子系统中,现在已经在等离子体纳米结构中实现[8,9].在众多等离子体纳米结构中,金属-绝缘体-金属(metal-insulator-metal,MIM)波导结构因具有易于集成,可靠性高,性能好等优点而被广泛关注[10,11].因此,基于Fano 共振的MIM 波导结构已经成为了微纳集成光子器件领域的一个研究热点[4,12-17].2016 年,Zhang 等[15]提出了一种MIM 波导耦合双矩形腔的等离子体纳米传感器,透射光谱表现为非对称的Fano 共振线型,其灵敏度可达596 nm/RIU (refractive index unit,RIU);2018 年,Liu 等[16]报道了一种基于可调谐Fano 共振的等离子体折射率传感器,由于该结构的对称破缺和明暗模式间的相干耦合而形成了尖锐的Fano 峰,其灵敏度可达600 nm/RIU;2021 年,Xiao 等[17]研究了一种基于Fano 共振的倒U 型谐振腔的高灵敏度等离子体传感器,最大的灵敏度为840 nm/RIU.传统的MIM 波导结构通常是通过改变结构的几何参数来调谐共振峰的谐振波长和线宽,从而实现该器件的性能调节.但是,这类器件一经制备其性能便被固化不可调谐.在实际应用中,动态可调的光学传感器件更受欢迎.相对于金属材料,石墨烯对SPPs 的局域限制力更强且传输损耗更低,因此新型石墨烯材料逐渐被引入了光学器件的研究[18,19].

石墨烯作为二维材料的典型代表,其结构是由碳原子经过SP2杂化后按照蜂巢晶格严密排列形成的六角形阵列,是一种零带隙半导体材料.石墨烯的电导率取决于带内跃迁和带间跃迁,通过外加偏置电压或化学掺杂可以实现表面电导率的动态调控[20-22].由于石墨烯内部碳原子独特的排布形式且作为导电性能最好的材料之一,其一经提出,便引起了国内外学者的广泛关注.目前,石墨烯已经迅速渗透到各个研究领域,如能源、电子、环境和化工等[23-26].在光电领域基于石墨烯材料的众多器件近年来也相继被报道.2018 年,Chen 等[19]提出了一种由单层石墨烯覆盖金属层的介质柱阵列构成的三维石墨烯超材料结构,该结构可实现太赫兹波入射下多个等离子体共振模式的有效激发.2019 年,Xiao 等[20]研究了一种可调谐交叉领结形石墨烯阵列结构等离子体折射率传感器,在中红外波段可获得双透射共振峰.2021 年,Dai 等[21]设计了一种由周期性单层石墨烯纳米带和多层电介质结构组成的混合结构,该结构中不同模式之间相干耦合产生的Fano 共振可应用为自参考折射率传感器.由文献[19-21]可知石墨烯已经被应用到纳米结构中,但他们所设计的结构都是二维石墨烯材料和三维腔体的结合.如果将二维石墨烯带卷曲为三维石墨烯纳米管结构,再与三维腔体结合,则可以使石墨烯材料与腔体在维度上更契合.

根据以上思路,本文提出了一种基于Fano 共振的MIM-石墨烯纳米管混合结构的动态可调折射率传感器.该器件不仅在维度上使石墨烯材料和腔体结构更加契合,而且在器件加工制备后可动态调节其共振峰的谐振波长和线宽,从而实现该器件的动态调控.通过有限元法 (finite element method,FEM) 对折射率传感器进行数值研究,并利用多模干涉耦合模理论 (multimode interference coupled mode theory,MICMT) 对该系统进行理论分析,其理论计算结果与FEM 数值仿真结果表现出高度一致性.结果表明,Fano 共振是由TM10腔共振模式和石墨烯电共振模式相干耦合形成的.通过改变石墨烯纳米管的化学势可以在较大波段范围内实现该系统共振峰的动态调控.本文还研究了腔体的几何参数对折射率传感器的性能影响.相比于以往报道的等离子体折射率传感器[15-17],该系统灵敏度可达1250 nm/RIU.研究结果为今后设计结构简单、动态可调的高性能纳米传感器提供了新思路.

2 模型建立和理论分析

本文提出的MIM-石墨烯纳米管混合结构示意图如图1 所示,由两个MIM 波导和一个内嵌石墨烯纳米管的圆环谐振腔组成.图1(a) 为三维模型结构,其中上层蓝色部分和橙色圆环部分分别表示Ag 和石墨烯纳米管,下层绿色部分为硅基底.由于仿真三维模型对计算设备的硬件配置和网格剖分有较高要求,而本文所研究的模型结构具有高度对称性,可以在柱坐标系下通过分离变量法降低求解的维度,即可将三维建模转化为二维建模[27-29].因此,采用FEM 方法进行二维几何建模与仿真计算.图1(b)为二维模型结构,其中橙色部分表示石墨烯纳米管,可以清楚地看出石墨烯纳米管将圆形腔分成内外两部分: 外部浅灰色圆环部分用空气填充;内部蓝色圆形部分用金属Ag 填充.这里Ag材料的一个重要作用是可以很好地支撑并固定石墨烯纳米管.入射波导S1和出射波导S2由空气填充且宽度相等,为确保该混合结构仅支持基本横向磁 (transverse magnetism,TM) 模式,其宽度固定为w=50 nm.石墨烯纳米管的厚度始终为d=3 nm,圆环腔半径为R,石墨烯纳米管外半径为R1,内半径R2=R1-d.两波导和内嵌石墨烯纳米管的圆环谐振腔之间的狭缝宽度相等,其宽度固定为g=10 nm.

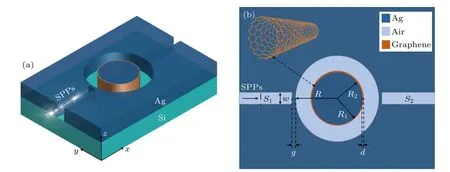
图1 MIM-石墨烯纳米管混合结构示意图 (a) 三维模型;(b) 二维模型Fig.1.The schematic of designed MIM-graphene nanotube: (a) 3D model;(b) 2D model.

在数值仿真过程中金属Ag 的相对介电常数可以由Drude 模型表示[3,17]

式中,无穷介电常数ε∞=3.7,等离子体振荡频率ωp=9.1 eV,阻尼系数Γ=0.018 eV,ω表示入射波的角频率.

石墨烯被视为一种单碳原子厚度约为0.34 nm的薄膜[21].在本文所研究的模型结构中,石墨烯纳米管厚度始终为3 nm,即约为9 层石墨烯薄膜.在数值计算过程中,工作范围为可见光到近红外波段,则带间跃迁对石墨烯电导率的贡献不可忽视.因此,石墨烯的光学电导率是由带间跃迁和带内跃迁共同决定,即σ(ω)=σintra+σinter.在石墨烯所处的环境温度T=300 K 下,kBT= 0.025852 eV,本文最小的石墨烯的化学势µc=0.5 eV,所以满足条件|µc|≫kBT.此时,石墨烯的带内跃迁电导率和带间跃迁电导率可以简化为[20,30,31]

式中,e为基本电荷量,kB为玻尔兹曼常数,为约化普朗克常数,τ为弛豫时间.

本文利用MICMT 分析验证该系统输入-输出的关系,共振模式之间的干涉会受到不同共振模式耦合相位的影响,因此需要考虑到耦合相位之间的关系.根据能量守恒,该多模耦合混合系统的相位方程满足[14,17,26]:

式中,φm是第m个谐振模式的总耦合相位差,ϕm为第m个谐振模式输入和输出端口之间的相位差.因为该混合结构中的输入波导S1和输出波导S2的几何参数相同,则τm=τm1=τm2且θm1=θm2.因此,该混合系统的透射率表达式可以简化为

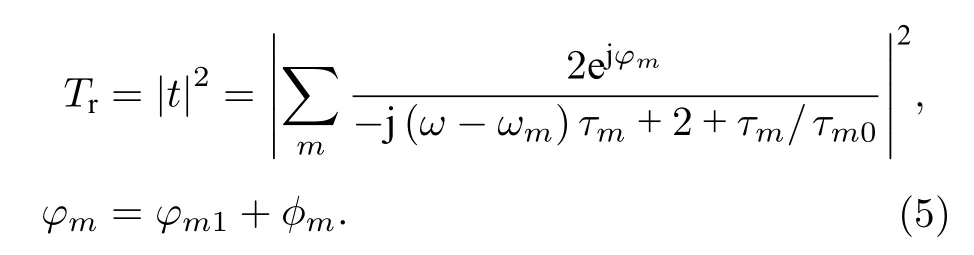
3 结果与讨论

为了说明所提出的混合结构的物理机制,将石墨烯的化学势设定为0.75 eV[26],其余未知参数分别设为R=180 nm,R1=90 nm.我们通过FEM分别对未加石墨烯纳米管 (将原石墨烯纳米管部分设置为Ag 材料) 和加入石墨烯纳米管的结构进行仿真分析,对比结果如图2(a)所示.当结构中未加入石墨烯纳米管时,其透射光谱如图2(a)蓝色实线所示,出现了两个Lorentz 峰,分别为峰IV 和峰V.波长是556 nm 的峰IV 透射率约为86.3%,该峰处的磁场图和电场图分别为图2(c),(e).波长是1054 nm 的峰V 透射率约为74.1%,其磁场图和电场图分别为图2(i),(m).当结构中加入石墨烯纳米管时,透射光谱如图2(a)紫色点划线所示,出现了两个Lorentz 峰和一个尖锐的Fano 峰,分别为峰I,峰II 和峰III,在峰II 和峰III 之间的波谷为Dip.波长是558 nm 的峰I 透射率约为63.3%,该峰处的磁场图和电场图分别为图2(b),(d)所示.波长是1042 nm 的峰II 透射率约为70.1%,其磁场图和电场图分别为图2(f),(j)所示.波长是1114 nm 的峰III 透射率约为47.2%,该峰处的磁场图和电场图分别为图2(h),(l)所示.波长是1096 nm 的波谷透射率约为0.016%,该波谷处的磁场图和电场图分别为图2(g),(k)所示.

图2 (a) 加入石墨烯纳米管结构前后的透射光谱对比;(b)—(m) 不同波长对应波峰、波谷处的磁场图(上)和电场图(下)Fig.2.(a) Comparison of transmission spectra with and without incorporated graphene nanotube structures;(b)—(m) magnetic field distribution (top) and electric field distribution (bottom) at the corresponding peaks and troughs at different wavelengths.

由图2(a)可知峰I 的透射率峰值比峰IV 的峰值低了约20%,起因是石墨烯纳米管对光的吸收.在可见光到近红外波段,单层石墨烯的光吸收率为2.3%[32].石墨烯层数较少时,由于其受周边层干扰非常小,因此总的光吸收率可以等效为互不作用的单层石墨烯吸收率的叠加,即石墨烯层的光吸收率与层数成比例[22].因此,该结构中加入石墨烯纳米管时,由于石墨烯纳米管的厚度约为9 层石墨烯薄膜,即石墨烯纳米管对光的吸收率约为20%,其与峰I 相比于峰IV 透射率的降低值相符合.

由峰II 和峰V 谐振波长处的磁场图和电场图可以看出其共振模式相同,均为TM10共振模式.将石墨烯纳米管引入MIM 波导耦合圆环谐振腔结构后,系统出现了一个非对称的Fano 峰 (峰III).这是因为石墨烯纳米管激发出了SPPs,其可由电场图2(k)中石墨烯纳米管的驻波共振现象得以验证.显然,石墨烯纳米管中激发出的等离子体共振模式是电模式.通过图2(k)可以看出,此时混合结构中的输出波导S2几乎无能量输出.因此,系统的透射光谱中出现了波谷.由以上分析可知,Fano 共振源自TM10腔共振模式与石墨烯电共振模式之间的相干耦合[26].

当MIM 波导耦合圆环谐振腔结构中加入石墨烯纳米管后,MIM-石墨烯纳米管混合结构成为了一个典型的多模干涉谐振器系统.通过对Fano 共振的物理分析,可知在800—1500 nm 的入射光波段内该系统存在TM10腔共振模式和石墨烯电共振模式,两种模式相互耦合形成了峰II 和峰III 两个透射峰.本文使用MICMT 对该混合结构的输入-输出关系进行理论分析.该系统利用FEM 仿真计算的结果和MICMT 理论计算的结果对比如图3所示,两条透射光谱表现出良好的一致性.在FEM仿真的基础上,利用MICMT 进行理论计算所得到的拟合参数结果如表1 所列.

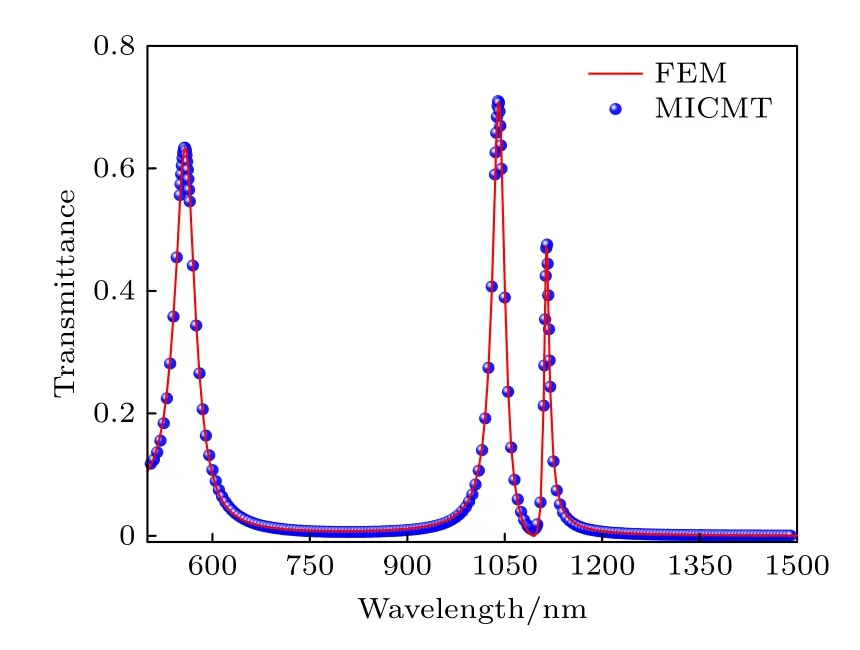
图3 MIM-石墨烯纳米管混合结构的仿真计算和理论分析对比Fig.3.Comparison of simulation calculation and theoretical analysis of MIM-graphene nanotube hybrid structure.

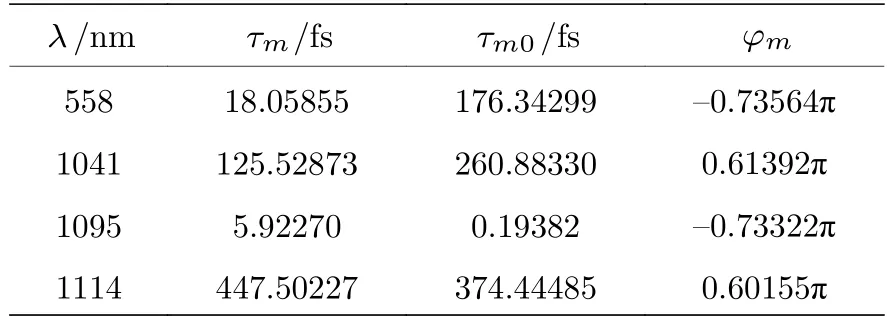
表1 拟合参数数值Table 1. Fitting parameter values.

通过外加偏置电压或化学掺杂等方式可以调节石墨烯纳米管的化学势µc,以此来实现MIM-石墨烯纳米管混合谐振腔系统的动态可调.当R=180 nm 和R1=90 nm 时,图4(a)为µc从0.65 eV以0.1 eV 为步长增大到0.95 eV 的透射光谱.由计算结果可以看出随着µc的增加,峰I 的谐振波长及透射强度基本不发生变化,而峰II 和峰III 的变化比较复杂,单独讨论图4(b)—(e).图4(f)为透射强度随入射波长和µc变化的关系图,可以看出TM10腔共振模式与石墨烯电共振模式之间的相干耦合而形成了两种混合模式.随着化学势的增加,一种混合模型移向了更低的波段,另一种混合模式移向了更高的波段,然而这两种混合模式之间并不交叉.随动态改变石墨烯的化学势,图4(b)—(e)中出现了这两种混合模式强耦合的拉比分裂(Rabi splitting),随着µc的增加峰III 在较宽波段范围内发生了蓝移且透射强度先增加后降低;此外,峰II的位置及透射强度基本不变,这是因为µc对石墨烯纳米管的电共振模式有较大影响,对腔内TM10共振模式几乎无影响.另外,已有研究表明石墨烯的化学势可以在近红外波段内动态调控等离子体结构的Fano 共振,改变其位置和寿命[33].而图4(c)中的峰II 相比于图4(b),(d),(e)中的峰II 发生了轻微蓝移,这是因为随着µc增加,波谷发生了蓝移,而µc=0.75 eV 时波谷刚好占据了部分峰II 的位置,进而使峰II 被迫产生了蓝移.

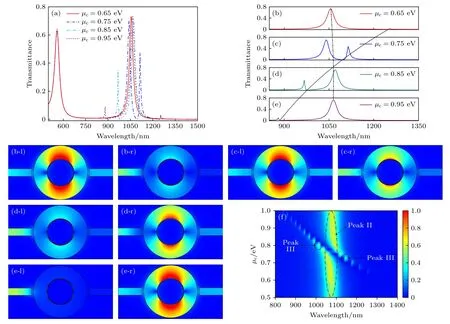
图4 (a) 随石墨烯化学势 µc 变化的透射光谱图;(b)—(e) 改变 µc 时仅峰II 和峰III 的透射光谱对比图; µ c=0.65 eV,峰II (b-l)和 峰III (b-r) 的电场图; µ c=0.75 eV,峰II (c-l) 和 峰III (c-r) 的电场图; µ c=0.85 eV,峰III (d-l) 和峰II (d-r) 的电场图;µc=0.95 eV,峰III (e-l) 和峰 II (e-r) 的电场图;(f) 透射强度随入射波长及 µc 变化的光谱图Fig.4.(a) Transmission spectra when changing the chemical potential of graphene;(b)—(e) comparison of transmission spectra of Peak II and Peak III only when changing the chemical potential of graphene;the electric field diagram of Peak II (b-l) and Peak III(b-r) at µ c=0.65 eV ;the electric field diagram of Peak II (c-l) and Peak III (c-r) at µ c=0.75 eV ;the electric field diagram of Peak III (d-l) and Peak II (d-r) at µ c=0.85 eV ;the electric field diagram of Peak III (e-l) and Peak II (e-r) at µ c=0.95 eV ;(f) spectra of the transmitted intensity with the variation incident wavelength and the chemical potential of graphene.

图4(b-l),(b-r),(c-l),(c-r)分别为µc=0.65 eV和 0.75 eV 时峰II 和峰III 的电场图,而图4(d-l),(d-r),(e-l),(e-r)分别为µc= 0.85 eV 和0.95 eV时峰III 和峰II 的电场图.由上述中的电场图可以看出峰II 均表现出更强的TM10腔共振模式特征,峰III 则均表现出更强的石墨烯电共振模式特征.因此,具有较宽透射带宽的峰II 是一种类似TM10腔共振的混合模式,而具有较窄透射带宽的峰III是一种类似石墨烯电共振的混合模式.显然,峰II和峰III 透射光谱的变化表明了这两种混合模式的转换过程.随着µc的增加,石墨烯电共振模式的能量增加并接近于TM10腔共振模式,因此,这两种模式之间的耦合会变得更强,TM10腔共振模式的更多特征被加入到类似石墨烯电共振的混合模式中,从而使得峰III 的透射峰展宽.当µc进一步增加时,尽管石墨烯电共振模式的能量也增强但其远离了TM10腔共振模式,则这两种模式之间的耦合会变弱,从而会使得峰III 的透射峰尖锐化.由以上分析可知,新型石墨烯材料的引入解决了传统MIM 波导结构传感器无法动态调控的问题.

灵敏度是衡量折射率传感器性能的重要指标,其表达式为[34]

式中,Δλ为共振峰波长的偏移量,Δn为空气折射率的变化量.图5 是R=180 nm,R1=90 nm 时共振峰的灵敏度S与µc的关系图,可以看出石墨烯纳米管的化学势对该系统传感性能的影响.显然,随着µc的增加,峰I 的灵敏度较稳定,然而峰II 和峰III 的灵敏度仅在µc=0.75 eV 附近时有较大的浮动.这是因为该系统在µc=0.75 eV 附近时峰III跨越峰II 发生了较大幅度的蓝移,即从峰II 的右侧蓝移到了峰II 的左侧.

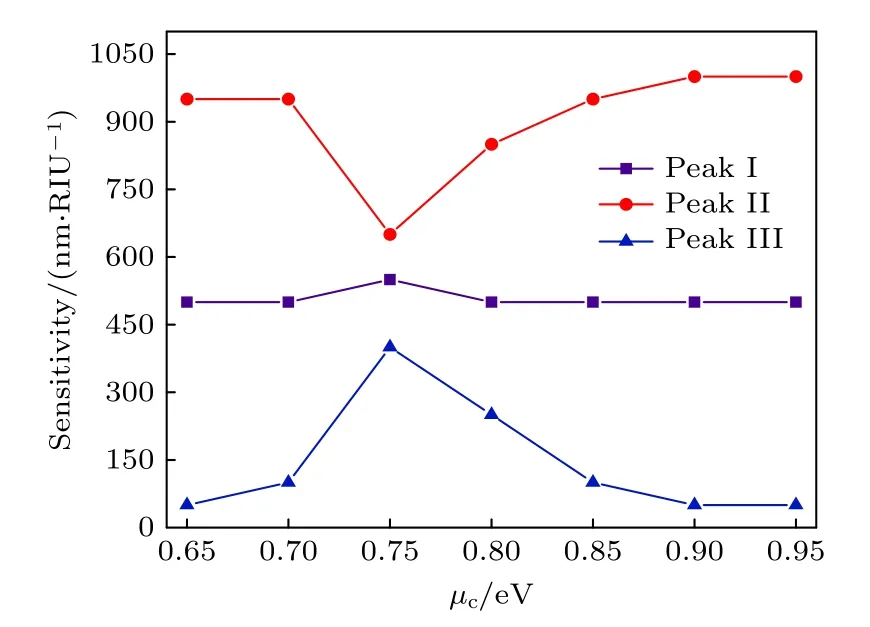
图5 3 个峰的灵敏度随 µc 的变化Fig.5.Sensitivity trends of three peaks when changing µc .

通常结构的几何参数对折射率传感器的性能有重要影响[15,16].接下来研究几何参数R和R1对该器件传感性能的影响,此时石墨烯的化学势固定为µc=0.75 eV .由图2(m)可看出仅在TM10腔共振模式下该系统透射强度高且在圆环谐振腔内能量集中,由此可预测到参数R和R1均对该模式有很大的影响.由图2(k)可以看出仅在石墨烯电共振模式下,该系统透射强度极低且电场能量主要被限制在石墨烯纳米管内,因此可预测到该模式几乎不受参数R的影响但受R1的影响.当研究R对传输特性影响时,令R1=90 nm.图6(a)为R由160 nm 以10 nm 为步长增大到200 nm 的透射光谱,峰I 发生了红移,其透射强度先增加后降低.这是由于该系统经历了欠耦合、临界耦合、过耦合三种状态[35].峰II 和峰III 也均发生了红移.峰II 的透射强度逐渐下降且尖锐化趋于Fano 共振的特性,峰III 透射强度逐渐增大且展宽趋于Lorentz共振的特性,而波谷的位置固定不变.当研究R1对传输特性影响时,令R=180 nm.图6(b)为R1由80 nm 以10 nm 为步长增大到110 nm 的透射光谱,随着R1的增加,峰I 发生了红移且透射强度越来越低,透射率降低主要是由于石墨烯纳米管半径增加使其对光的吸收率增加引起的.而峰II 和峰III 变化趋势较复杂,如图6(c)所示,峰II 和峰III 均发生了红移.这是因为石墨烯纳米管半径增大使得石墨烯的占空比变大,而谐振波长与石墨烯的占空比呈正相关[20],即.同时由图6(c)可以看出峰II 的透射强度逐渐下降且尖锐化呈Fano 共振的特性,峰III 的透射强度逐渐增大且展宽呈Lorentz 共振的特性.图6(a),(b)对比发现,相比于参数R,R1对峰II 和峰III的影响更大.这是因为R1对TM10腔共振模式和石墨烯电共振模式均有很大的影响,而R仅对TM10共振模式有很大的影响.所以R1对由TM10腔共振模式与石墨烯电共振模式相干耦合形成的峰II 和峰III 影响更大,该结论与上述预测一致.

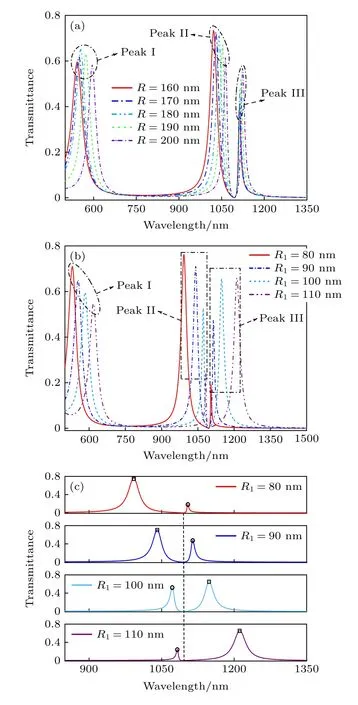
图6 (a),(b) 改变R 和R1 的透射光谱;(c) 改变R1 时仅峰II 和峰III 的透射光谱(矩形框为Lorentz 峰,圆形框为Fano 峰)Fig.6.(a),(b) Transmission spectra with different parameters R and R1;(c) transmission spectra of Peak II and Peak III only with different parameters R1 (Rectangular frame is Lorentz peak,round frame is Fano peak).

图7(a)是R1=90 nm 时共振峰的灵敏度S与R的关系图,图7(b)是R=180 nm 时共振峰的灵敏度S与R1的关系图,此时µc=0.75 eV .通过图7(a),(b)可以清楚地看出几何参数变化对该系统传感特性的影响.随着R或R1的增加,3 个共振峰灵敏度的趋势表现出一致性: 峰I 的灵敏度较稳定,峰II 的灵敏度呈降低趋势,峰III 的灵敏度呈增加趋势.峰I 的灵敏度呈现较稳定的趋势,是因为峰I 仅发生了透射强度的变化,并没有Fano 共振和Lorentz 共振之间的转化.而峰II 和峰III 的灵敏度之所以随着R或R1的增加呈现出相反的变化趋势,是由于峰II 和峰III 会受R或R1的影响而实现Fano 共振和Lorentz 共振之间的相互转化.由图6(a),(b)可以看出随着R或R1的增加,峰II 由原本的Lorentz 共振逐渐呈现出了Fano 共振的特性,然而峰III 由原本的Fano 共振逐渐呈现出了Lorentz 共振的特性.

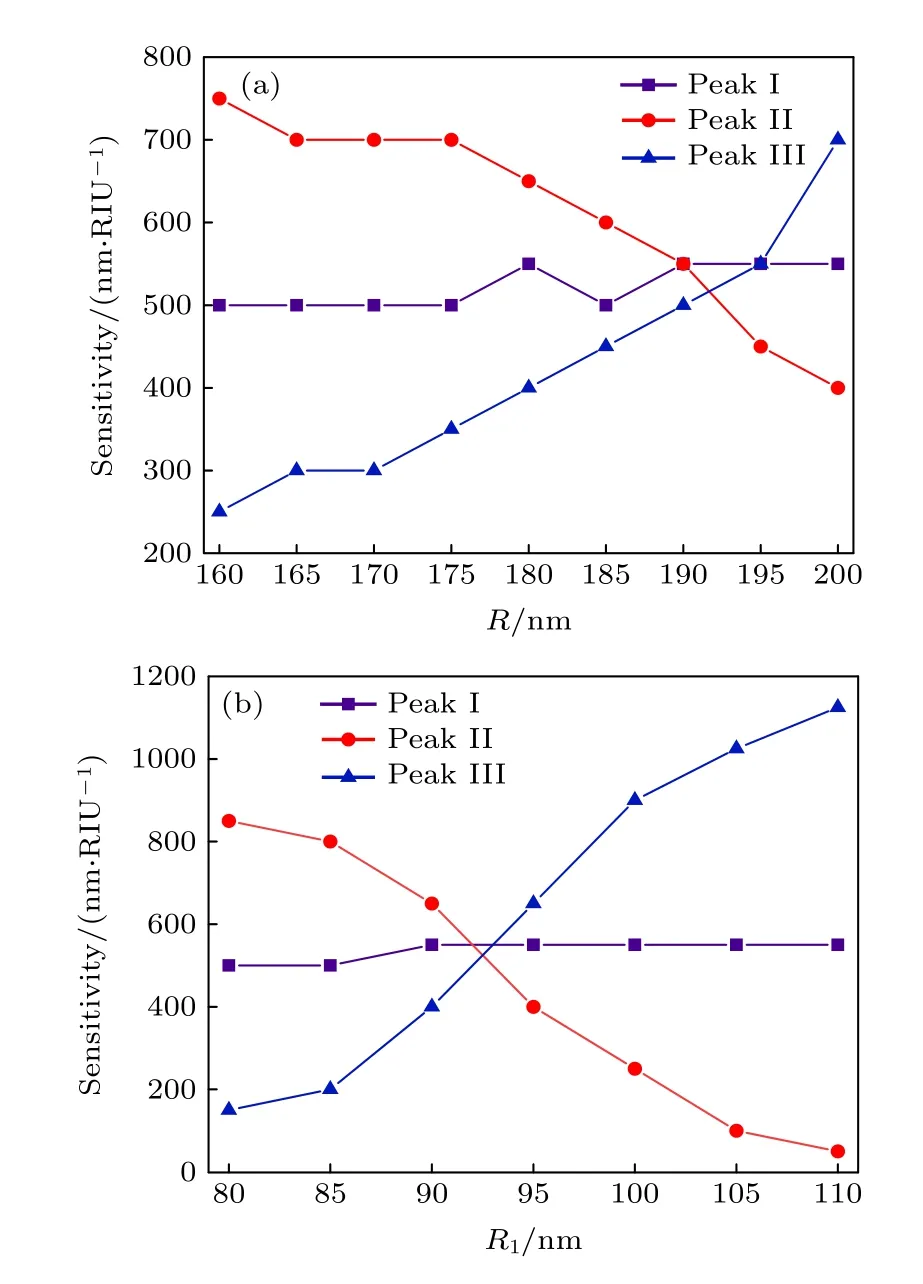
图7 3 个峰的灵敏度随参数R 和R1 的变化Fig.7.Sensitivity trends of the three peaks with different parameters R and R1.

此外,品质因数 (figure of merit,FOM) 也是衡量传感器性能的重要指标,其表达式为[36]

式中,S为折射率传感器的灵敏度,F WHM 为共振峰的半峰全宽.FOM 数值越大,说明传感器的性能越好.

通过对折射率传感器各个参数分析研究,可以知道该传感器的最佳参数为R=180 nm,R1=110 nm,µc=0.75 eV .在最佳参数设置下,峰II转化为了标准的Fano 峰,而峰III 则转化为了标准的Lorentz 峰.本文所设计的折射率传感器主要是针对气体传感.在最佳参数设置下,可以将图1混合结构中的空气换成其他待测气体环境,则该外部气体环境折射率n以0.02 RIU 为步长由1.00 增加到1.10 的透射光谱对比如图8 所示.由计算结果可以看出,随着n的增加,峰I 和峰III 均发生了明显的红移且透射峰峰值基本不变,而峰II 发生了轻微的红移且 F WHM 越来越窄.由(6)式可以计算出共振峰峰I,峰II 和峰III 的折射率灵敏度分别为500,250,1250 nm/RIU.由(7)式可以计算出共振峰峰I,峰II 和峰III 的品质因数分别为12.5,42.4,41.7 RIU—1.由此可见,该系统具有良好的传感性能.

图8 改变折射率 n 的透射光谱对比图Fig.8.Comparison of transmission spectra with different refractive indexes n.

虽然本文只是数值模拟和理论计算的结果,并没有进行实验研究,但是该系统的结构制备和实验演示是可以预期的.该折射率传感器结构可以利用聚焦离子束刻蚀技术和化学气相沉积法进行制备.具体制备过程如下: 首先,利用聚焦离子束在无粘附层的银金属薄膜上按照所设计的MIM 波导耦合圆环谐振腔金属纳米结构的轮廓刻蚀得到密闭的纳米沟槽,然后利用透明胶带有选择地剥离掉沟槽中对该金属结构来说多余的金属膜部分,最终在硅衬底上得到分离的MIM 波导耦合圆环谐振腔金属纳米结构[37].之后利用化学气相沉积法制作出管径合适的石墨烯纳米管[38].接下来,将石墨烯纳米管与其生长的催化剂金属分离并将其转移到MIM波导耦合圆环谐振腔金属纳米结构中的银柱外侧.最后,样品可以通过光谱测试系统进行实验测试.

4 结论

本文提出了一种动态可调的MIM-石墨烯纳米管混合结构传感器系统.通过有限元数值仿真和MICMT 理论验证相结合的形式,对该系统进行了深入研究.结果表明,石墨烯材料的引入,使该系统形成了一个Fano 峰.该共振峰源自于TM10腔共振模式和石墨烯等离子体电共振模式之间的相干耦合.通过改变石墨烯的化学势可在较大波段范围内实现共振峰的动态调谐,从而解决了传统的等离子体折射率传感器不可动态调控的问题.此外,还详细研究了结构的几何参数对该系统传感性能的影响.最佳参数设置下,该系统的灵敏度可达1250 nm/RIU,品质因数可达42.4 RIU—1.本文所设计的结构用作折射率传感器不仅具有很高的实际应用价值,还为设计动态可调的新型亚波长纳米传感器提供了设计思路与理论参考.