宇称-时间对称与反对称研究进展*

唐原江 梁超 刘永椿

1) (清华大学物理系,低维量子物理国家重点实验室,北京 100084)

2) (教育部量子信息前沿科学中心,北京 100084)

在标准量子力学中,描述物理系统的哈密顿量一般是厄米的,以保证系统具有实能谱及系统演化的幺正性.近些年来,研究发现具有宇称-时间(parity-time,P T)对称特性的非厄米哈密顿量也具有实能谱,并且在PT 对称相和 PT 对称破缺相之间存在一个新奇的非厄米奇异点,这是厄米系统所不具有的.最近,人们在各种各样的物理系统中实现了 PT 对称和 PT 反对称的非厄米哈密顿量,并演示了新奇的量子现象,这不仅加深了对基本量子物理规律的理解,也促进了应用技术的突破.本综述将介绍 PT 对称和 PT 反对称的基本物理原理,总结在光学系统和原子系统中实现 PT 对称和 PT 反对称的方案,并回顾利用 PT 对称系统非厄米奇异点进行精密传感的研究.

1 引言

标准的量子力学对系统进行描述时引入了一条基本假设: 系统的哈密顿量为厄米的.这一基本假设保证了系统的能量本征值为实数,同时也保证了系统的量子态在演化过程中的概率守恒.一直以来,非厄米的哈密顿量仅被用来唯象地描述耗散系统,然而,研究者们在非厄米哈密顿量中找到了大量具有实数本征值的算符,这引发了对非厄米哈密顿量的极大关注[1].1998 年,Bender 和Boettcher[2]提出空间反演(P)和时间反演(T)共同作用下不变的非厄米哈密顿量也可以有实数本征值(此类算符被简称为PT算符).随着系统参量的变化,PT算符描述的系统可以处于PT对称相或者PT破缺相,处于PT对称相的系统具有实数的本征值,处于PT破缺相的系统有一对共轭的本征值,两个相的分界点为非厄米系统特有的奇异点(exceptional point,非厄米奇异点)[3],在该点处系统的本征态和本征值同时合并在一起.

PT对称性的研究引领了理论物理各个领域的新发展,包括量子场论[4]、李代数[5]等.PT对称的概念被引入光学系统后,很快成为了研究的热点.随着PT对称光学系统的构建和对其特性的深入研究,发现了基于PT对称的大量新奇效应和应用,例如双折射[6]、功率振荡[7-9]、非互易性光传播[10-12]、单向不可见性[13-15]、单模激光器[16,17],轨道角动量激光器[18,19]等.除了光学系统外,人们也在其他各种系统中对PT对称展开了广泛的研究,如原子系统[20,21]、电子学系统[22-24]、NV 色心系统[25]、光力学系统[26,27]、声学系统[28,29]和微波系统[30]等.

随着对PT对称系统研究的深入,人们又提出了具有PT反对称特性的新系统[31-41].PT对称系统的哈密顿量在P和T的联合操作下形式不变,作为与PT对称相对偶的概念,PT反对称系统的哈密顿量在P和T联合操作下形式与原来相反,出现一个负号.PT反对称系统呈现出与PT对称系统对偶的特性,例如PT对称系统中的无损耗传播对应到PT反对称系统中就是无折射传播,这为光的控制提供了崭新的概念和技术手段,大大扩展了非厄米光学的研究范围.

目前已有许多相关综述,例如,光学和光子学中的PT对称综述[42-47]、利用相干原子实现PT对称综述[48],基于PT对称的人工合成激光综述[49]、PT对称中的非线性综述[50,51]等.本文的侧重点主要是综合PT对称和PT反对称两种系统,以展现两者的诸多类似之处以及各自的独特性质.

本文首先介绍了PT对称与PT反对称哈密顿量,然后介绍在光学系统和原子系统中PT对称的实现,进而介绍光学系统和原子系统PT反对称的典型研究,以及基于PT对称系统中非厄米奇异点的精密传感研究.

2 PT 对称与反对称哈密顿量

在量子力学中,可观测物理量需要用厄米算符来表示,因此系统的哈密顿量也需要用厄米算符表示,这不仅可以确保其本征值为实数,而且可以确保波函数随时间的演化过程中的模值不变[52].1998 年,Bender 和Boettcher[2]提出空间反演P和时间反演T共同作用下不变的非厄米哈密顿量也可以有实数的本征值.在空间反演变换下,坐标和动量算符有如下变换:

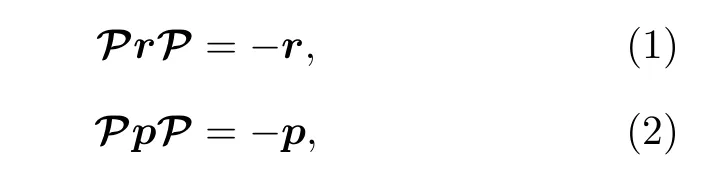
其中,r和p分别为坐标算符和动量算符.在时间反演变换下:

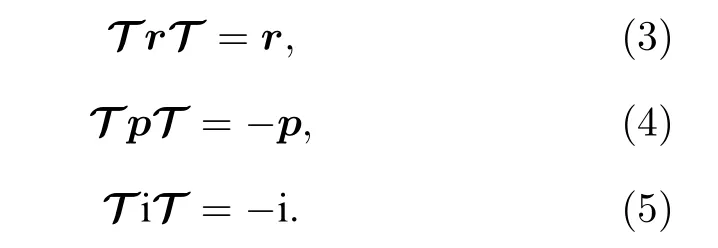
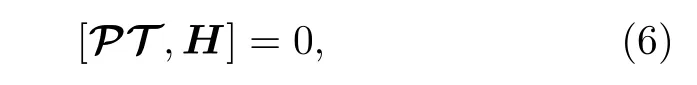
则系统的哈密顿量满足PT对称性.由以上对易关系系统的哈密顿算符满足PT对称的一个必要条件,是其中的势能项满足:

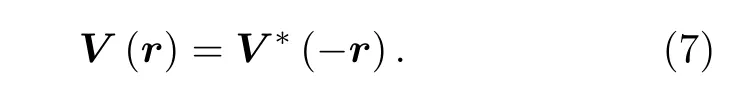
考虑二能级(模式)系统,如图1(a)所示,两个模式耦合构成的系统可以被如下PT对称哈密顿量描述:

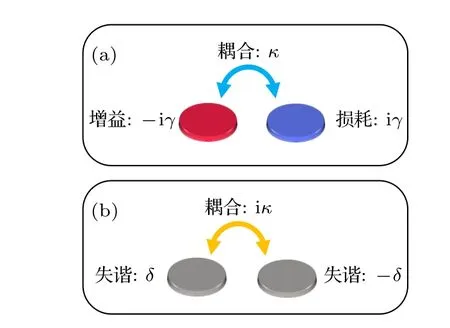
图1 P T 对称系统(a)与 PT 反对称系统(b)示意图Fig.1.Schematic diagram of PT -symmetric system (a)and anti-P T symmetric system (b).

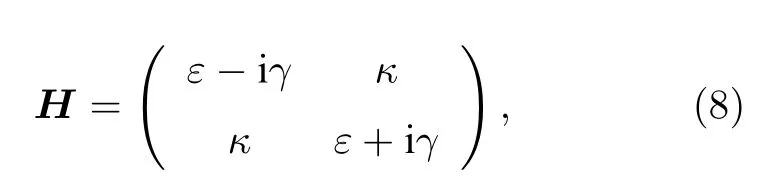
其中,两个共振模式的能量由能级ε描述,两个模式分别为增益和耗散模式,增益和耗散速率由γ描述,两个模式间的耦合系数为κ.

与PT对称系统相比,PT反对称系统的非厄米哈密顿算符H满足如下反对易关系:

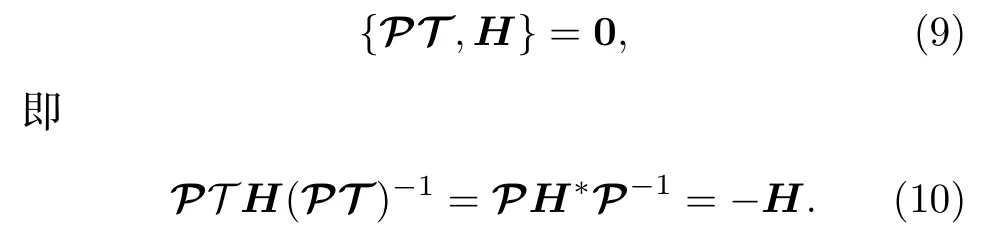
以二能级(模式)系统为例,如图1(b)所示,相应的PT反对称哈密顿量为

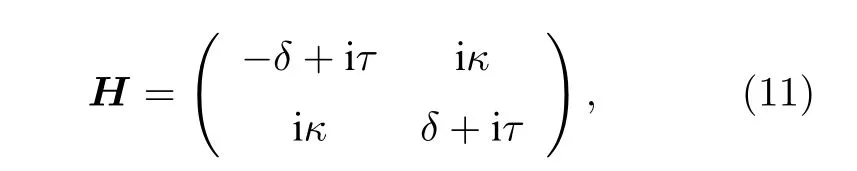
其中,两个模式的能级偏移分别为-δ和δ,增益或者耗散速率由|τ|描 述,两个模式间的耦合系数为 iκ.

3 光学系统中的 PT 对称

基于光学傍轴波动方程和量子力学薛定谔方程之间的形式等价性,人们提出了在光学框架内实现PT对称势的方案[6,14,53].例如,考虑光波导中的光场传输方程:

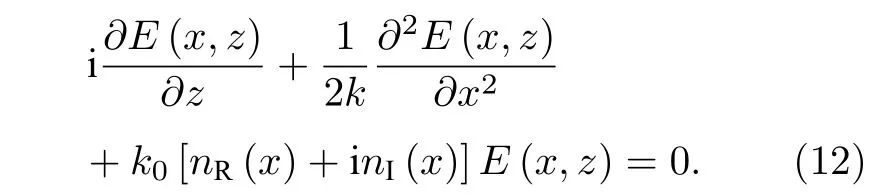
其中,E(x,z) 为电场强度的慢变振幅,k=k0n0为介质中的波矢,k0=2π/λ0为真空中的波矢,λ0为真空中的波长,n0为介质折射率(系统的折射率分别为n0+nR(x)+inI(x)).方程(12)与如下薛定谔方程具有相同的形式:

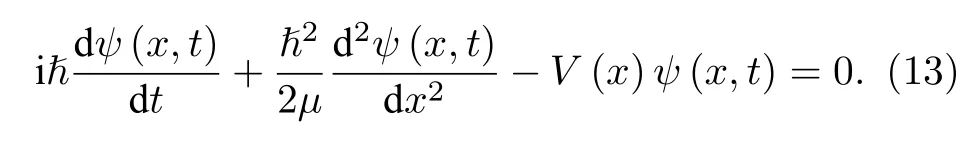
其中ψ(x,t) 为波函数,ℏ 为普朗克常数,µ为粒子质量,V(x) 为势能函数.对比两个方程得到对应关系为

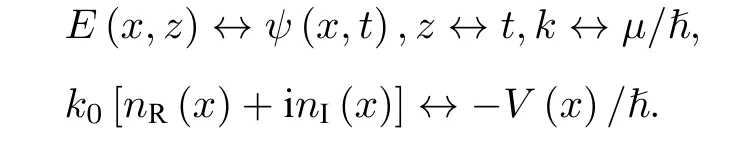
由于折射率分布与量子力学的势能部分相对应,由方程(7)中PT对称系统的势能项满足的关系可以得出,PT对称光学系统的折射率实部为坐标x的偶函数,折射率的虚部为坐标x的奇函数:

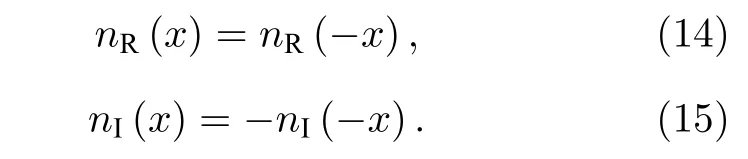
2010 年,Rüter 等[9]提出了PT对称的耦合波导光学系统并进行了实验研究.如图2 所示,系统为两波导耦合系统,其中一个波导中的光具有大小为γ的损耗系数,对另一个波导进行泵浦,使该波导中的光获得大小为γ的有效增益系数,从而构造出了满足PT对称的复折射率分布.通过耦合模方法,两个耦合波导中的光场动力学可以用下面的方程描述:

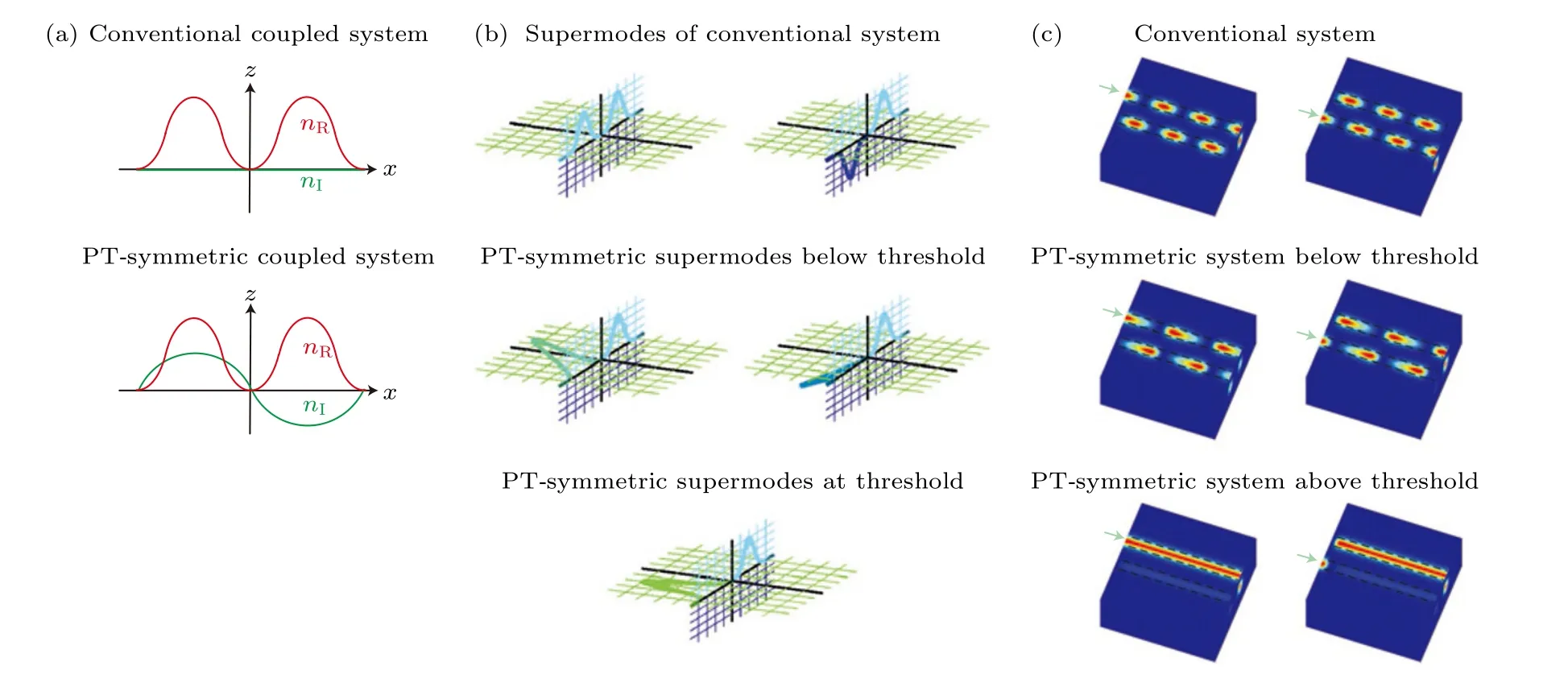
图2 传统和 PT 对称耦合光学系统 (a) 复折射率的实部(n R,红线)和虚部(nI,绿线)分布;(b) 传统和PT 对称系统的叠加态;(c) 对于传统和 PT 对称系统,当系统在通道1 或通道2 处被激发时的光波传播情况 [9]Fig.2.Conventional and PT -symmetric optical systems: (a) The distribution of real part (n R,red line) and imaginary part (nI green line) of the complex refractive index;(b) superposition state of conventional and PT-symmetric systems;(c) light wave propagation when the system is excited at channel 1 or channel 2 [9].

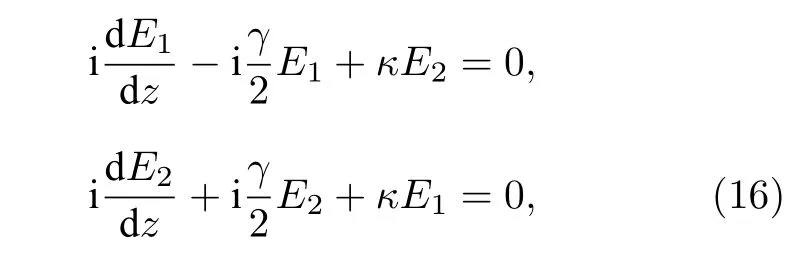
其中E1和E2分别表示波导1 和波导2 中模式场的幅值,κ为两个波导模式的耦合系数.系统可以用如下的哈密顿量描述:

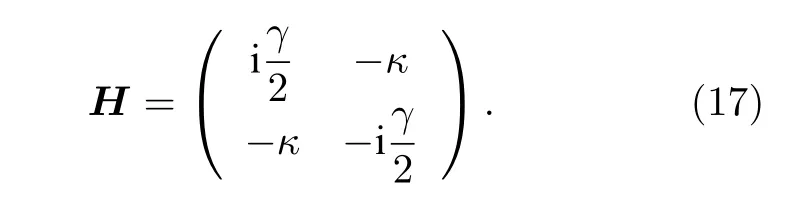
当γ＜2κ时,系统处于PT对称相,系统的本征值为

其中 s inθ=γ/2κ.此时两个本征值的虚部为零,实部劈裂,相应的本征态为

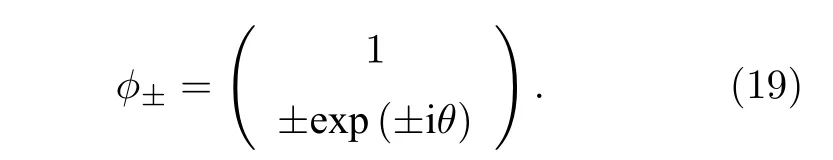
显然,处于PT对称相的模式满足|E1|=|E2|,这意味着本征态的强度在两个波导中均匀分布,因此模式经历了平衡的增益和损耗,导致其本征值的虚部为零.此外,随着γ/2κ从0 增大到1,θ从0 逐渐增大到 π /2 .

当γ＞2κ时,系统处于PT对称破缺相,系统的本征值为

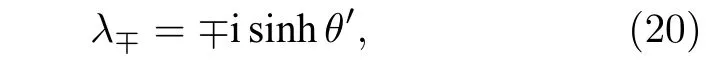
其中 c oshθ′=γ/(2κ) .此时两个本征值的实部相等,虚部劈裂,相应的本征态为

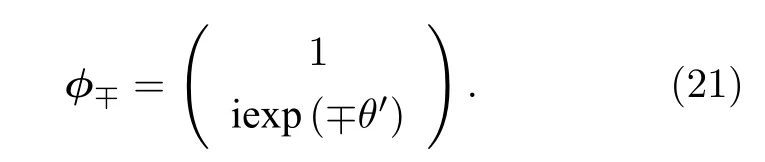
处于PT对称破缺相的系统,随着γ/(2κ) 从1 开始逐渐增大,θ′从0 开始逐渐增大,显然,|E12|,这意味着一个本征态主要局域在增益波导,另一个本征态主要局域在损耗波导,导致本征值的虚部劈裂.

当γ=2κ时,系统处于PT对称相与PT对称破缺相的相变点,即为非厄米奇异点,系统的本征值为

此时本征值的实部和虚部同时合并,相应的本征态为

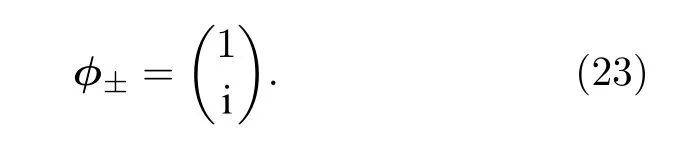
处于非厄米奇异点的系统,不仅本征值合并在一起,本征态也合并为同一个模式.

与厄米系统不同,这些本征模不再是正交的,这对光束动力学有重要影响,例如会产生非对称传输特性和功率振荡等现象.对于传统的厄米系统,两个本征模(对称和反对称,见图2(b))的任何叠加都会导致对称的波传播: 显然,图2(c)的上部分图中的光场分布具有左右对称性.当耦合系统涉及增益/损耗时,系统的特性与厄米系统的特性不再相同.在PT对称相,随着γ/(2κ) 从0 开始增大,本征态的两个模式分量之间的相对相位差分别从0 和 π 处的初始值逐渐增大,当γ/(2κ) 增大到1 时,系统处于非厄米奇异点.此时光传播表现出非对称传输特性: 将输入通道从波导1 交换到波导2 时,获得了完全不同的输出状态.在PT对称破缺相,无论光从波导1 输入还是从波导2 输入,光总是从波导1 输出,再次表现出了非对称传输的特性(见图2(c)底部的图).这是因为系统的本征值为复数,相应的模式振幅指数增大或者耗散,只有一个模式存留下来.

4 原子系统中的 PT 对称

近年来,研究发现在原子系统中也可以实现PT对称.中山大学罗乐课题组[54]与中国人民大学张威、张翔课题组[55]分别利用超冷原子和单个囚禁离子构造了PT对称系统,并对其量子演化过程进行了测量,同时引入周期性的含时系统哈密顿量,对系统的相图等进行研究,如图3 所示.下面将以在单个囚禁离子系统中的实现方案为例进行说明.

考虑具有PT对称性的单量子比特非厄米哈密顿量:

囚禁离子系统是量子模拟、量子计算等研究平台之一,具有与环境耦合小、参数可控性高等优点,可以进行量子态层析投影测量,能够测量态占据数和密度矩阵相干项的演化(见图3(c)).由此出发,该课题组发现了两组和实验参数无关的初态和测量态,可以直接由体系演化测量结果得到体系的能量值,而体系能量值为零的点对应该体系的非厄米奇异点.在此基础上,课题组引入周期性的驱动和耗散,将定态哈密顿量扩展为含时哈密顿量,并测量了系统的能量和相图(图3(d)),而且观测到系统哈密顿量的周期与量子态耦合强度满足一定条件下发生的多光子共振现象.

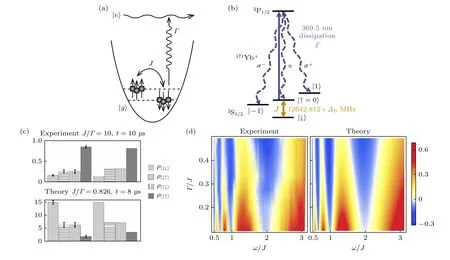
图3 (a) 在冷原子系统中实现 PT 对称的示意图[54];(b) 在单个囚禁离子系统中实现 PT 对称的镱离子 1 71Yb+ 的能级示意图[55];(c) 系统密度矩阵测量图[55];(d) 系统的相图[55],红色和黄色区域对应 PT 对称相,蓝色区域对应 PT 对称破缺相Fig.3.(a) Schematic diagram of realizing PT symmetry in cold atom system[54];(b) schematic diagram of energy levels of ytterbium ion 1 71Yb+ for realizing PT symmetry in a single trapped ion system[55];(c) system density matrix measurement diagram[55];(d) the phase diagram of the system[55].The red and yellow areas correspond to the PT -symmetric phase,and the blue area corresponds to the PT -symmetry-broken phase.

5 光学系统中的 PT 反对称

PT反对称光学系统有很多奇特的性质,如连续谱激光[34]、光完全单向无反射传播[33]、模式选择的光放大[32]和散射中心决定的散射特性[40,41]等.2017 年,清华大学尤力、刘永椿课题组[31]提出了利用间接耗散耦合在光学系统中实现PT反对称哈密顿量的方法.2019 年,吉林大学张旭霖课题组、香港科技大学陈子亭课题组[37]利用该方法在波导系统中实现了光的手性传输.

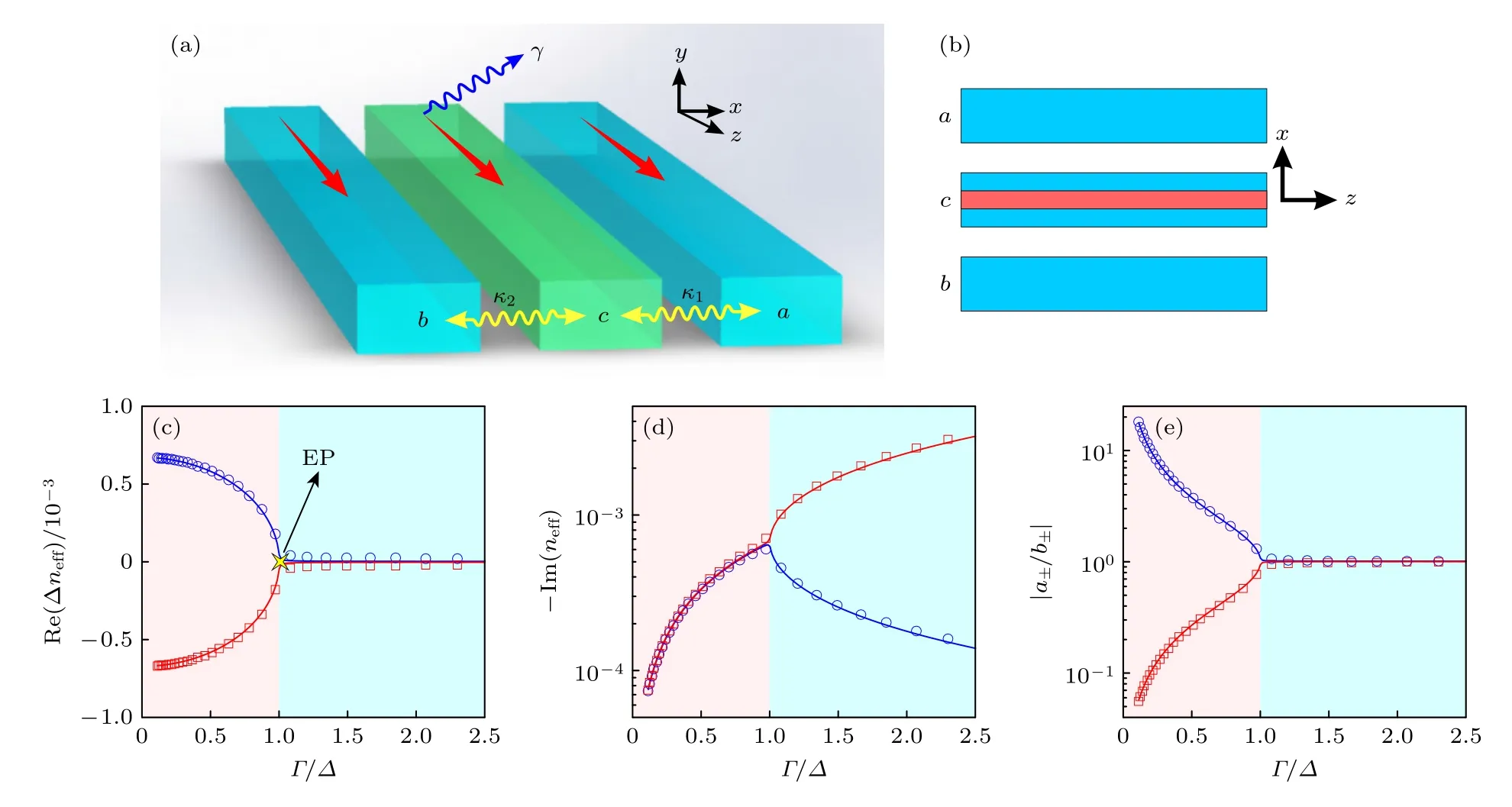
图4 (a) 耦合波导示意图;(b) 耦合波导的截面示意图,波导 c 红色部分表示存在较大耗散;(c),(d) 波导本征模式的特性;(e) 波导场强的特性;数据点是有限元模拟结果,实线是理论计算结果[31]Fig.4.(a) Schematic diagram of coupled waveguide;(b) cross section diagram of coupled waveguide,the red part of waveguide c indicates large dissipation;(c),(d) characteristics of waveguide eigenmodes;(e) property of waveguide field strength.Data points are finite element simulation results,and solid lines are theoretical calculation results[31].

PT相变过程会显著改变系统的传输特性,利用演化算符U(z)=e-iHz可以得到在两个相中的分束比例随着光沿z方向传播的变化:

时域的PT反对称同样可利用间接耦合在光学微腔(如图6(a),(b))中进行构建.用来描述系统的状态,系统的演化方程可以写成i∂tΨ=HΨ,其中

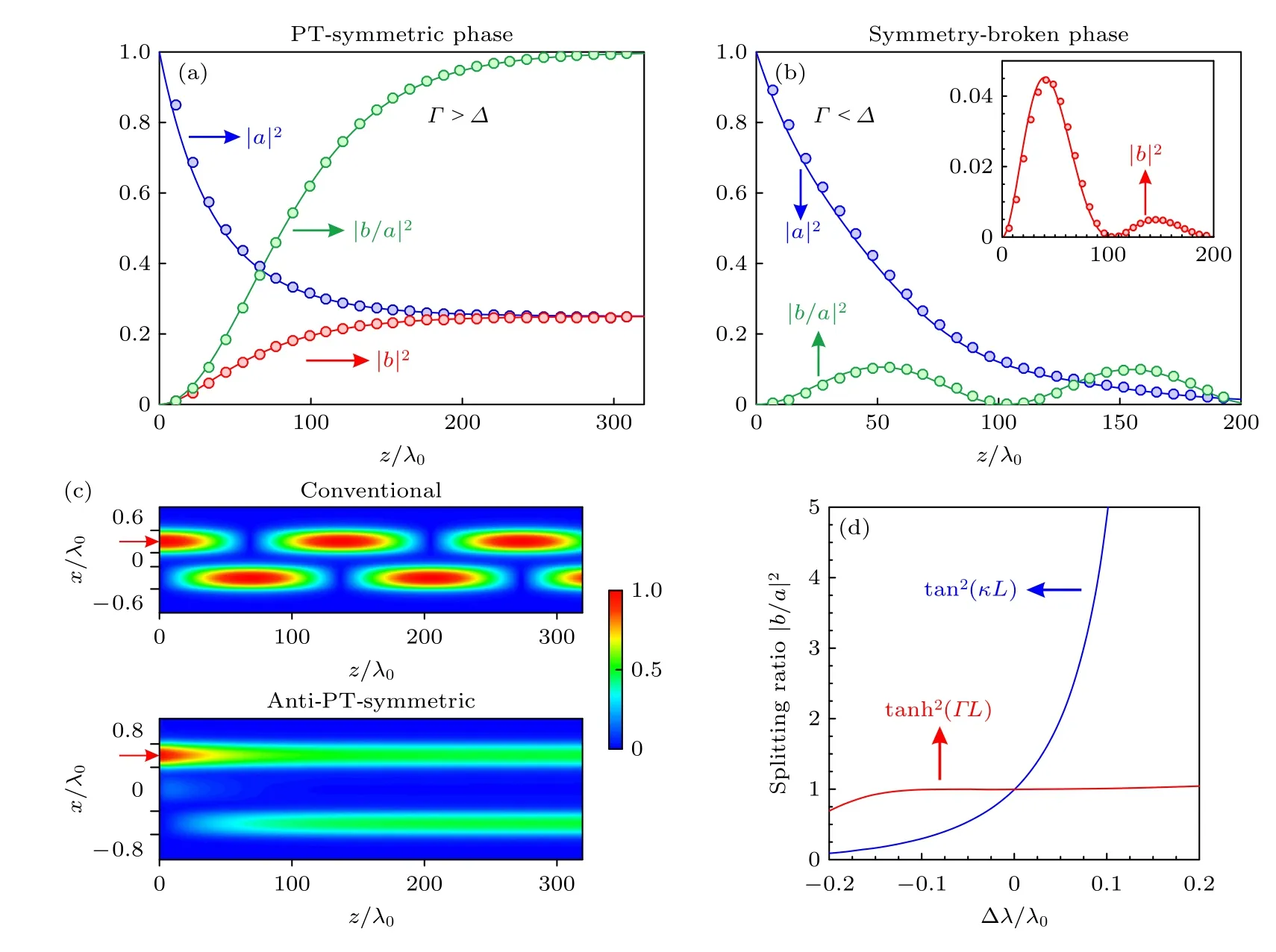
图5 波导内的光场演化图 [31] (a),(b) PT 对称相和 PT 对称破缺相的传播特性,数据点是有限元模拟结果,实线是理论计算结果;(c) 传统厄米系统和 PT 反对称系统的光场分布对比图;(d) 分束比例对波长的依赖特性,红色线是 PT 反对称系统,蓝色线是传统厄米系统Fig.5.Evolution diagram of light field in the waveguides[31]: (a) (b) The propagation characteristics of PT -symmetric phase and PT-symmetry-broken phase,respectively,the data points are the result of finite element simulation,and the solid lines are the result of theoretical calculation;(c) comparison diagram of light field distribution between traditional Hermitian system and anti-PTsymmetric system;(d) the dependence of beam splitting ratio on wavelength,the red line is the anti-P T -symmetric system,and the blue line is the traditional Hermitian system.

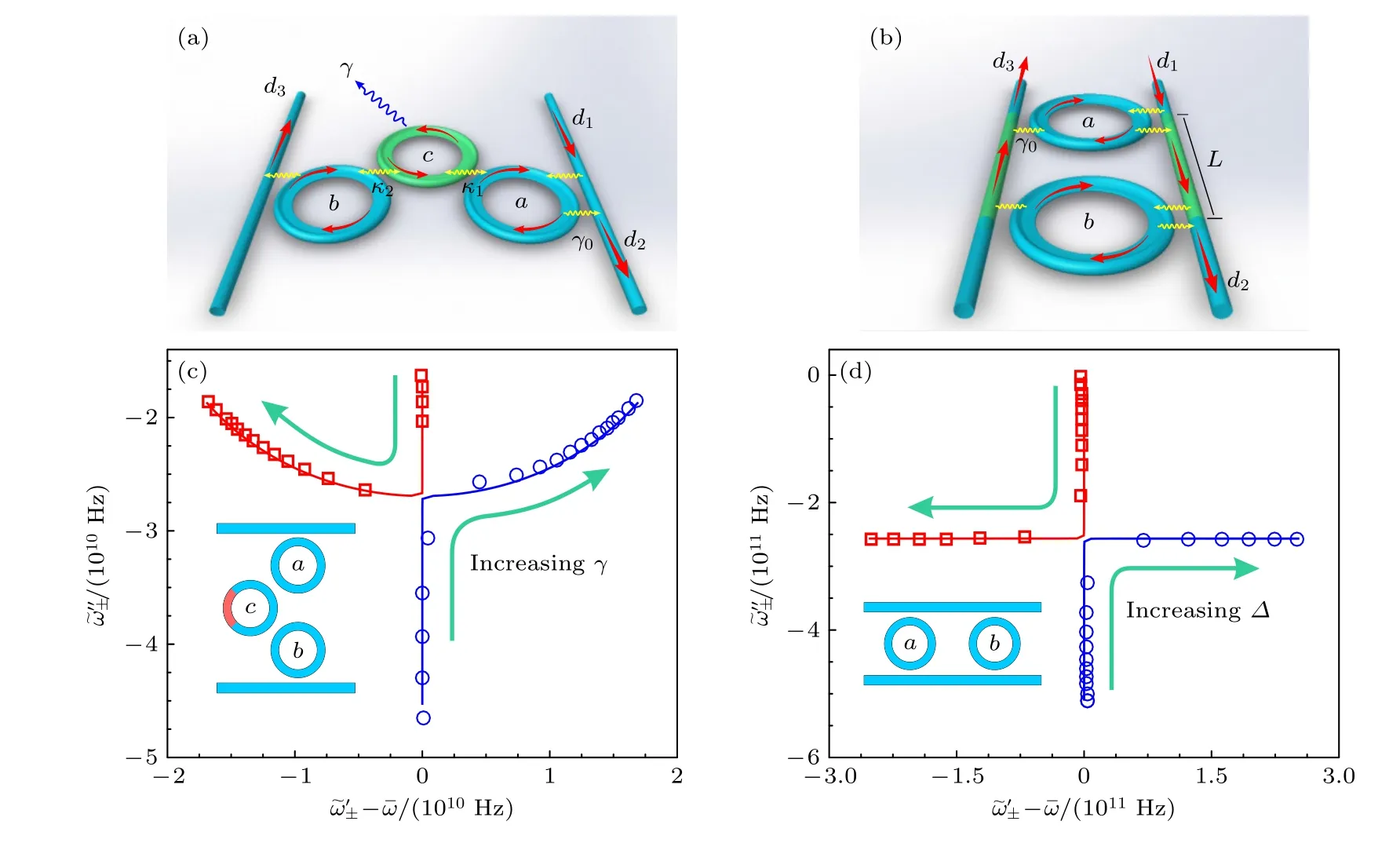
图6 光学微腔构型I (a)和构型II (b)及相应本征频率在复平面上的演化(c)(d),数据点是有限元模拟结果,实线是理论计算结果 [31]Fig.6.Optical microcavity configuration I (a) and configuration II (b) and the corresponding eigenfrequencies on the complex plane.Data points are finite element simulation results,and solid lines are theoretical calculation results[31].

6 原子系统中的 PT 反对称

2016 年,复旦大学肖艳红课题组[38]在原子系统中实现了宇称-时间反对称的哈密顿量.在该研究中,利用原子的热运动构建了光学模式之间的耦合.如图7(a)所示,实验在87Rb 原子气室中进行,温度约为40 ℃.气室的内表面覆盖着不破坏量子态相干的石蜡,这使原子能够经受数千次与壁的碰撞,而不会破坏其内部量子态.原子蒸汽室被封装在一个四层屏蔽层内,从而屏蔽环境磁场.在屏蔽层内部,利用螺线管产生均匀的磁场,该磁场可诱导一个塞曼位移δB到双光子失谐上.利用半波片(HWP)和偏振分束器(PBS)将来自腔外半导体激光器(ECDL)的一束激光分为4 束.探测光和控制光(具有正交线性偏振)首先通过1/4 波片(QWP)重新组合并转换为圆偏振,然后被引导到两个相距1 cm 的光学通道(称为Ch1 和Ch2).Ch1 和Ch2的能级结构如图7(b)所示,Ch1 和Ch2 中的右旋圆偏振控制场分别与跃迁|1〉→|3〉共振;而Ch1 和Ch2 中的左旋圆偏振控制场分别与跃迁|2〉→|3〉近似共振,但与共振频率在相反方向上偏移了相同的大小|Δ0|,其中Δ0是探测光和控制光频率之间的差值.Δ0利用声光调制器产生,为了稳定探测光和控制光之间的相位关系,所有声光调制器都由彼此间相位固定不变的振荡器驱动.在每个通道中,共同传播的探针光和控制光构建了 Λ 型EIT 效应,并产生了寿命约为100 ms的基态相干性.一个光通道中的光和原子相互作用,改变了原子的量子态,然后该原子通过热运进入另外一个光通道,与另一个通道的光相互作用,将之前通道内的光的信息传递给这束光,从而实现了两个通道内的光模式之间的间接耦合.两个自旋波通过气室中87Rb 原子的运动自然耦合,在一些特定的近似下,两个集体自旋波激发的动力学可以由以下非厄米哈密顿量Heff来描述:

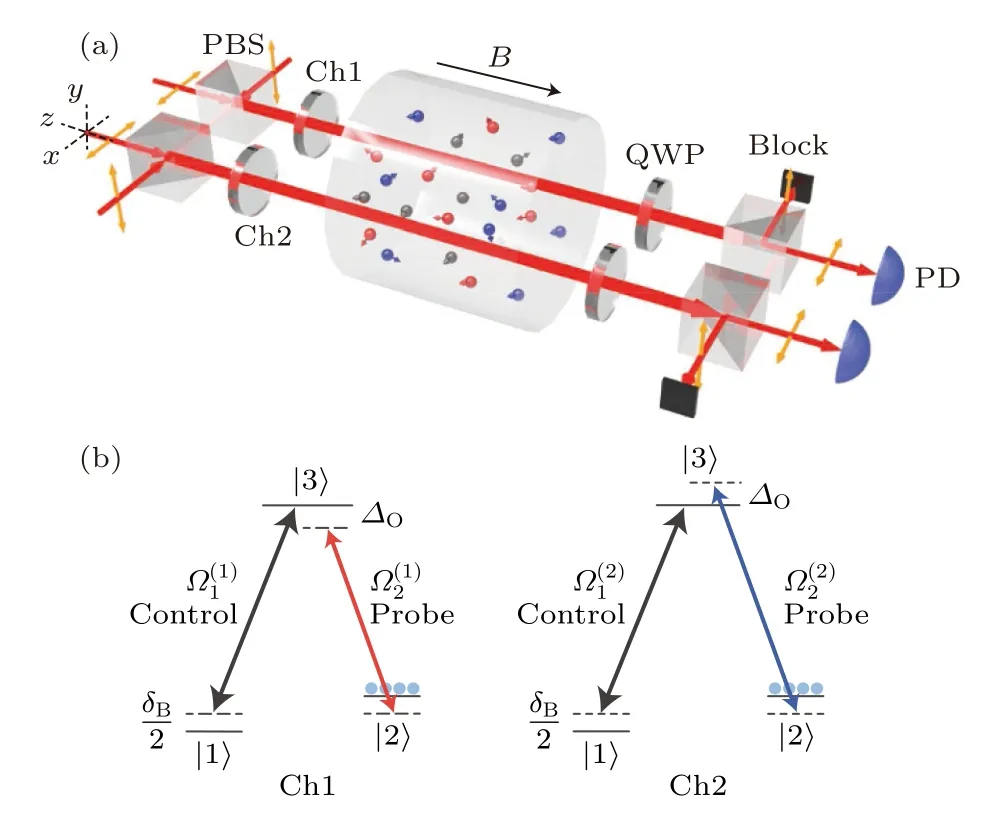
图7 (a) 通过热 87Rb 蒸汽池中的快速原子相干传输,实现 PT 反对称 性的示意图;(b) 两个通道中的三能级Λ型EIT 构型 [38]Fig.7.(a) Schematic diagram of realizing anti-P T -symmetry through fast atomic coherent transmission in hot 87Rb vapor cell;(b) three level Λ-type EIT configuration in two channels[38].

此 2×2 哈密顿量H满足{PT,H}=0,为PT反对称的哈密顿量.

该工作在实验上能观察到了相变现象,在对称相,两个光模式的谐振峰位置完全重合;在对称破缺相,两个光模式的谐振峰位置劈裂.由于原子的量子态寿命较长,因此相变的观测精度达到了1 Hz 级别.在此PT反对称系统中,在体系对称性破缺前,虽然两束光经过的介质的折射率不同,但实现了无折射传播.

7 基于非厄米奇异点的传感

由于PT对称与反对称系统中存在非厄米奇异点,因此在精密传感领域有重要的应用价值.在厄米系统中,微扰(|ε|≪1)引起的本征谱的偏移或劈裂最多与微扰ε自身在一个阶次上.对于N个模式合并所对应的N阶非厄米奇异点,本征频率分裂 Δω对外界微扰具有ε1/N的依赖关系.当外界微扰|ε|≪1 时,与厄米系统相比,在非厄米系统的奇异点附近可以极大地提高对外界微扰的探测灵敏度.理论与实验结果表明,二阶非厄米奇异点可以增强谐振模式对外部扰动的敏感性[56,57],而使用更高阶非厄米奇异点在原则上可以进一步提高系统对外界微扰响应的灵敏度.

2017 年,美国Khajavikhan 课题组[58]利用耦合腔构造了具有3 个模式的PT对称系统,实验证明了系统中存在高阶非厄米奇异点,且系统对外界微扰的响应表现出对微扰强度的立方根特性.如图8 所示,系统由3 个谐振腔组成: 增益腔和损耗腔被无增益和损耗的中性腔隔开,两侧的环形腔的增益和损耗强度相等,环形腔之间以相同的耦合强度交换能量.此PT对称系统的模场的演化由如下方程决定:

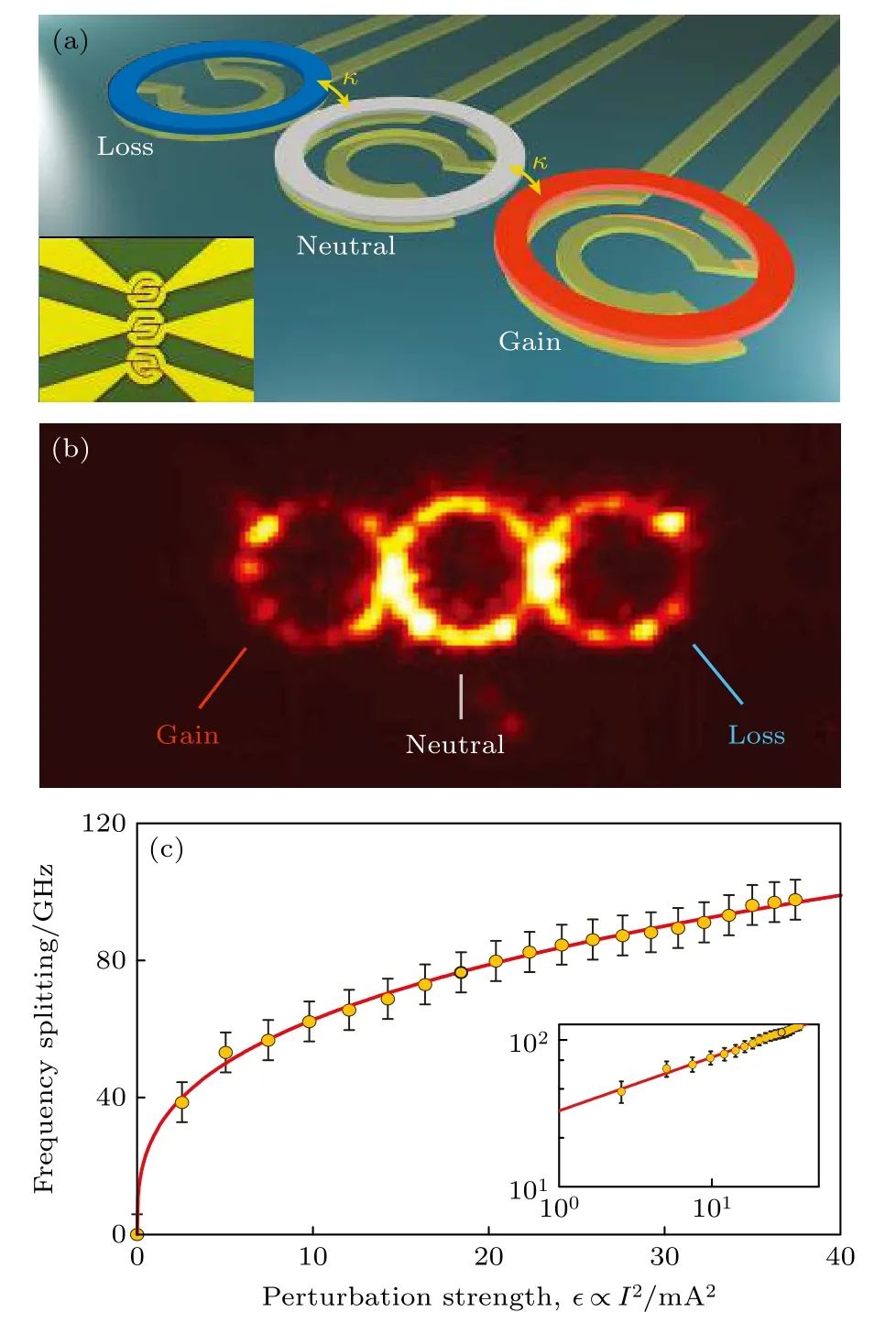
图8 (a) 3 个等距微环腔构成的 PT 对称系统示意图,两侧的谐振腔具有平衡的增益和损耗,而中间的谐振腔是中性的;(b) 系统处于三阶非厄米奇异点的激光模式的强度分布;(c) 相邻激光谱线之间的分裂随微扰强度 ε 的变化,数据点是实验测量结果,实线是理论计算结果[58]Fig.8.(a) Schematic diagram of PT -symmetric system composed of three equidistant micro-ring cavities,the resonators on both sides have balanced gain and loss,while the resonators in the middle are neutral;(b) the intensity distribution of the laser mode with the system at the third-order non-Hermitian exception point;(c) splitting between adjacent laser spectral lines with perturbation intensity ε .Data points are experimental measurement results,and solid lines are theoretical calculation results[58].

其中,g和-g分别描述增益和损耗,ε为在增益环形腔上加的外界微扰.

当系统不存在微扰时(ε=0 ),假设V对时间的依赖关系为,则系统本征频率可以通过求解如下方程得到:

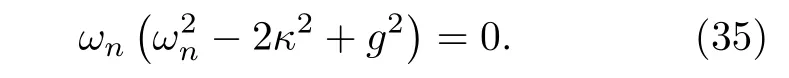
当系统环形腔的增益和损耗强度g和环形腔之间的耦合强度κ满足时,系统的3 个本征频率合并为相同的ωn=0,与此同时,系统3 个本征矢量合并为相同的其中A0为归一化常数.此时系统处于三阶非厄米奇异点,当系统受到微扰ε时,系统的本征频率频率发生劈裂,该课题组求解得到了系统本征频率对外界微扰依赖关系的近似解析表达式,并进行了数值求解验证,在此基础上,该课题组实验证明了系统相邻本征频率的劈裂与微扰强度之间具有三次方根的形式.这表明,与传统的微腔传感器相比,此系统对足够小的微扰的探测灵敏度有极大提高.

尽管这些实验已经证明在奇异点处可以获得劈裂增强,但没有仔细考虑噪声的变化.之后的一些分析显示奇异点附近的噪声也得到了增强,因此对于信噪比来说并没有提高[59].目前,相关方面的研究仍然在进行中,例如在文献 [60]中通过发展量子噪声理论来计算奇异点传感器的信噪比性能,利用量子Fisher 信息来确定信噪比的下限,结果表明奇异点传感器是有可能改善信噪比的,在实验方面,基于奇异点探测器增强的Sagnac 效应[61],基于六阶奇异点PT对称电路的灵敏度增强传感[62],基于奇异点增强信噪比的加速度计[63]等实验也已经实现.

8 总结与展望

本文介绍了PT对称和反对称的基本物理原理,主要回顾了PT对称和反对称在光学系统和原子系统中的理论和实验实现,并介绍了基于非厄米奇异点的精密传感研究.在未来,关于PT对称和反对称的研究有望进一步加深对相关基础理论的理解,以及在多个领域获得应用.

在理论方面,尽管PT对称量子力学的数学形式已经比较完善,但大部分研究中只考虑了经典区域,例如将经典波动方程写成类似于薛定谔方程的形式.如果进一步考虑更一般性的量子效应,有可能揭示更加丰富的物理.例如,由于PT对称与反对称系统中具有增益和耗散,这与量子涨落-耗散定理、量子噪声等有本质联系,因此可以探索系统中的量子涨落和噪声等[64,65].

PT对称的相关变体也PT大的研究价值.例如,PT对称中的操作可以被另一种空间操作(例如旋转)所取代[66,67].这将进一步扩展相关领域.此外,基于PT对称启发的对称范式,如超对称性、非厄米粒子-空穴对称性[68]等也是一个重要的发展方向.例如,超对称性可为设计光学结构提供有效的工具[69],在光通信等领域有广泛应用[70].不仅如此,近年来,在光学系统中非PT对称复势(即的研究也引起了关注,在这种情况下也可以保证哈密顿量具有实能谱[71-73],可以实现单向无反射的光传输[74],非局域孤子[75]等.

除了在理论方面的发展,在具体应用方面,PT对称的光子系统可能为未来集成光子学器件的实现提供一条新的途径.实际应用的物理器件不可避免地与环境有耦合导致耗散的存在,而PT对称系统可以巧妙地设计增益模式,可以有效地补偿损耗或者放大光脉冲,也可以设计高效可集成的新型光开关、单向非反射光学器件[11,12]、CPA 激光器[49]、声子激光器[76]等新型器件.除了在光学系统中的应用外,在原子系统中,利用PT对称原理实现耦合调控,也为构造新型光子器件和原子器件提供了新的思路.