石英晶体板非线性高频振动的拓展伽辽金法分析

吴荣兴，王晓明，张青艳，王 骥

(1.宁波职业技术学院应用力学研究所，宁波 315800；2.宁波大学机械与力学学院,宁波 315211)

0 引 言

随着现代电子行业和物联网技术的不断发展，石英晶体谐振器作为稳定频率和选择频率的关键元件，在通信、医疗传感、航天航空、工程检测等领域有着广泛的应用[1-4]。石英晶体谐振器高频振动分析的方法有Mindlin、Lee和Peach等提出的各种板理论和基于这些理论的有限元分析[5-8]。在石英晶片的小变形和不考虑高阶材料常数的情况下，Mindlin等[5]板理论将位移展开为厚度坐标的幂级数从而将三维弹性问题转化为二维问题。随着电子元器件尺寸的不断微型化和工作频率的不断提高，尺寸效应和高阶材料常数的影响也逐渐体现[9-10]。

Tiersten等[11-12]首先建立了考虑材料非线性的压电板高频振动方程，并引入了高阶材料常数和偏场效应，用摄动法等解析法对简化后的方程进行了求解。Yang等[13]建立了考虑大变形情况下石英晶体谐振器的非线性高频振动方程，并用伽辽金法和摄动法等对非线性方程进行了求解。Abe等[14]分别利用Mindlin板理论和有限元法对压电晶体板的非线性高频振动进行了分析。Wu等[15-17]建立了考虑几何和材料非线性的石英晶体板的高频振动方程，但是仅对单一厚度剪切振动方程进行了求解。Wang等提出了扩展伽辽金法(extended Galerkin method, EGM)和扩展瑞利-里兹法(extended Rayleigh-Ritz method, ERRM)，其主要思路就是对非线性方程在时间上取一个振动周期的平均，从而将微分方程化为代数方程，根据非线性问题的周期平均特性实现近似和相应的简化[18-21]。在此基础上，本文利用扩展伽辽金法对石英晶体板非线性高频振动方程组进行了转化和求解。

1 非线性方程求解

随着压电声波器件尺寸的微型化和振动频率的高频化，高阶材料常数和几何大变形对压电声波器件振动特性的影响也越来越明显[10,14]。Wu等[15-17]建立了考虑几何和材料非线性的石英晶体板的厚度剪切振动模态和弯曲振动模态的控制方程，具体表达式如下:

(1)

和

(2)

Wu等[15-17]建立的石英晶体板高频振动非线性方程组不仅考虑了几何和材料非线性，而且考虑了电场的影响，无法直接求解。Wang和Wu等利用传统的伽辽金法对单一厚度剪切振动的非线性振动方程式(2)进行转化，接着分别利用摄动法和同伦分析法等对该非线性方程进行了求解[15-17]。对于强烈耦合的非线性方程组式(1)和式(2)，Wang等利用逐次逼近法对方程进行了求解，获得的结果不是特别理想[15-17]。本文希望用拓展伽辽金法对强烈耦合的石英晶体板高频振动方程组进行联合求解。

可以定义两个残差为:

(3)

和

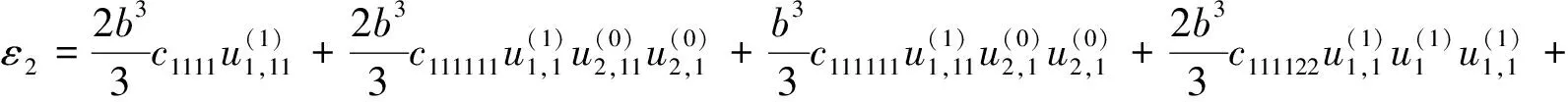
(4)

传统的伽辽金法利用线性解的正交性将非线性偏微分方程转化为时间变量的常微分方程[24]，Wang等提出的拓展伽辽金法在平衡方程的加权函数中添加简谐函数并对一定周期内进行积分，可以得到振动特性的代数方程[18-21]。具体表达式如下[18-21]:

(5)

式中:a和T分别为石英晶体板的半板长和一个周期。

根据石英晶体谐振器的位移和电势的直峰波假设[13]，可以假设:

(6)

式中:A(B)、m(n)、ω和V分别是两个模态的振幅、波数、振动频率和石英晶体谐振器的驱动电压。根据Wang等石英晶片的最佳长厚比尺寸选取，这里可以设定两个模态的波数为m=14,n=1。

基于位移假设，重写式(5)为：

(7)

拓展伽辽金法可以提供对不同周期的时间函数积分，得到低阶和高阶的频幅关系，并通过振幅迭代获得更为精确的位移解和频率表达式[19]。

将位移表达式(6)代入残差表达式(3)和式(4)，最后代入式(7)，可以得到:

(8)

和

(9)

式中：

(10)

重写式(8)和式(9)，可以得到：

(11)

和

(12)

2 数值算例

式(11)和式(12)就是考虑几何和材料非线性的石英晶体板的厚度剪切振动模态和弯曲振动模态强烈耦合的频率响应方程组。为了避免两种模态的强烈耦合，选取最佳尺寸为b=0.827 3 mm,a=21.2b。为了计算简单，定义归一化振动频率为Z=ω/ωTSh0。根据石英晶体材料常数和选取的石英晶片尺寸，通过Matlab程序对式(11)和式(12)进行数值求解，分别绘制弯曲振动模态和厚度剪切振动模态的频率响应关系如图2和图3所示。

图2和图3都表明厚度剪切振动模态和弯曲振动模态的位移均为纳米级别，这与试验观测到的结果一致[3]。图2表明随着归一化振动频率Z的增加，弯曲振动模态方程首先观察到弯曲振动模态达到谐振状态，在归一化振动频率1附近，可以观察到厚度剪切振动模态的谐振状态。图3表明厚度剪切振动模态在归一化振动频率1附近达到谐振状态，没有观察到弯曲振动模态的谐振，主要原因是弯曲振动的振幅相对于厚度剪切振动的振幅较小，大约为厚度剪切振动模态振幅的量级，因此观察不到该振动的谐振[15-17]。

可以对式(12)进行改写，省略纯弯曲振动模态的部分且保留耦合部分可以得到[15-17]：

(13)

式中：P1=D3+αD4+α2D5+α3D6，α=A/B为新定义的振幅比。

根据Yang提出的电位移近似理论[25]，流经石英晶体板上下电极的单位面积的电流可以表示为:

I=e26BωTSh0

(14)

根据式(14)，可以得到:

(15)

这样就获得了石英晶体板厚度剪切振动模态的频率响应方程。可以进一步绘制不同振幅比和不同驱动电压情况下的频率响应曲线如图4和图5所示。这里需要指出的是图4和图5的横坐标为厚度剪切振动模态基频的百万分之一(parts per million)，因此没有单位[15-17]。

图4为不同振幅比情况的石英晶体板非线性厚度剪切振动模态的频率响应曲线，其驱动电压V为1 V。图4表明随着振幅比α的增加，频率响应曲线整体向右弯，出现了硬弹簧特性的趋势[13,15-17]。因此在实际石英晶体谐振器高频振动分析过程中，必须考虑弯曲振动模态的耦合，也就是利用Wang等提出的最佳长厚比尺寸来避免两种模态的强烈耦合[22-23]。这里的结果表明过去对石英晶体板单一厚度剪切振动的求解存在一定缺陷，因为弯曲振动模态的振幅对厚度剪切振动的影响非常明显，只有利用拓展伽辽金法对石英晶体板高频振动非线性方程组进行联合求解才能获得精确的振动特性分析[13,15-17]。

图5为不同驱动电压下石英晶体板厚度剪切振动模态的频率响应曲线，其振幅比为α=0.02。表明随着驱动电压的增加，石英晶体谐振器的频率漂移也将更加明显，也就是石英晶体谐振器的激励电平效应开始出现[14]。例如当I=100 A/m2时，各驱动电压之间的频率漂移普遍在30×10-6左右，实际压电谐振器的允许频率漂移值一般在10×10-6以内[15-17]。因此在石英晶体谐振器的实际使用过程中，必须对驱动电压进行精确控制。

3 结 论

利用扩展伽辽金法对考虑几何和材料非线性的石英晶体板厚度剪切振动和弯曲振动的方程组进行了转化和求解，分别获得了强烈耦合的弯曲振动模态和厚度剪切振动模态的频率响应关系，绘制了不同振幅比和不同驱动电压影响下的频率响应曲线图。数值计算结果表明，当选取石英晶片的最佳长厚比尺寸时，厚度剪切振动模态是石英晶体谐振器的主要模态，而弯曲振动模态的耦合较小。当选取其他不同石英晶片的长厚比尺寸时，振幅比的影响将较为明显。同时发现不同驱动电压对石英晶体谐振器厚度剪切振动的振动频率影响极为明显，频率漂移值超出了压电声波器件的允许值。这里得到的结果可以部分解释石英晶体谐振器的激励电平效应，在实际石英晶体谐振器的工作过程中，必须保持驱动电压的稳定性。