基于Auto CAD二次开发的露天矿DTM曲面快速构建计算研究*

2022-09-14范振华李角群付信凯卢皎旭程相琛

现代矿业 2022年8期

范振华李角群付信凯卢皎旭高松程相琛

（1.中钢集团山东富全矿业有限公司；2.西安建筑科技大学资源工程学院；3.陕西省矿产资源综合利用工程技术研究中心）

我国露天矿设计是对拟建露天矿的开拓、开采等主要生产系统、辅助环节、配套设施和安全措施等进行全面设计［1-2］，而露天矿终了境界设计是露天矿设计的核心，其第一步就是露天矿基础境界优化设计，即一次境界设计。目前国内一次境界主要的获取方法有传统的作图法［1］、近似优化的浮锥法［2］、优化的LG 法等［3］。后2 种需要建立矿床模型、经济模型，再由相关专业软件自动圈定，完成露天矿境界优化设计［4］。林友等［5］描述了人工完成终了境界设计过程，阐述了凹陷短露天矿境界出入沟的设计方法与技巧，并结合设计实例在AutoCAD 软件中实现。张中雷等［6］利用3Dmine 软件建立矿区的数字表面模型，并进行运输道路优化设计、首采工作面布置以及开拓工程量计算等。目前可以完成露天矿终了境界设计的软件包括 SURPAC、MICROMINE、DIMINE、3DMINE 等［7］，但在实际设计应用中并不尽善尽美，对于复杂的二次境界设计显得无能为力，还需繁重的人工作图。AutoCAD 作为一款优秀计算机辅助设计软件，自从其诞生以来就有非常强的影响力，到目前为止，其已经成为三维矢量绘图建模软件的国际标准。

借助AutoCAD 软件强大的功能以及开放的二次开发技术，以露天矿终了境界设计为研究对象，对于露天矿终了境界设计绘图中DTM 曲面的快速构建及切割技术进行研究，目标是构建基于AutoCAD 平台的DTM 曲面构建程序模块，解放设计人员的繁琐作图劳作，能够快速、准确完成绘图任务，提高工作效率和质量。

1 露天矿基础境界设计

露天矿基础境界优化设计即一次境界设计，其设计基础是地质矿床模型，首先需要设定境界设计原则，之后再依据某些优化算法完成露天矿的境界优化设计。通常采用净现值最大原则，依据浮锥法、LG 法等进行一次境界优化设计圈定［1-4］。一次境界设计中并没有考虑开拓运输系统，境界边坡角也是在满足边坡安全条件下取最大值，其最大成果是获取露天矿底部位置与形态。在一次境界优化设计基础上，通过对露天矿底部周界（可以是多底）、境界边坡角布置整理，构建出一次境界DTM 曲面，以此切割出各个台阶境界线，为后续开拓布线提供依据，再结合地表DTM 模型，将二者进行一系列的剪切运算即可得到露天矿终了境界模型。

1.1 基础数据准备

（1）绘图比例设定。露天矿终了境界图一般绘图比例为1∶1 000，考虑到打印出图，也可以看到绘图为1∶2 000 的比例。事实上，只要有坐标网格的图纸，在AutoCAD软件中永远采用1∶1 000比例绘制。

（2）露天矿底部周界处理。经过境界优化设计确定的底部周界线仅仅是确定了底部标高和大致形态，底部周界线需要局部修匀处理，为使终了境界线尽可能平滑，底部周界线采用样条曲线。样条曲线优点在于其平滑性。

（3）境界边坡角布置。由于露天矿开采面积较大，终了境界所处矿岩物理力学性质也不尽相同，因此通过岩石力学模拟计算或矿山类比，可以在一次境界优化设计确定境界边坡角分布信息。通过在平面图上绘制出各个区域多边形以确定境界边坡角的位置，再以图形扩展数据技术将境界边坡角存储在各个区域多边形中，以备后续二次境界设计应用，见图1。

1.2 一次境界顶部与底部周界绘制

如前所述，底部周界最初整理为样条曲线，其目的是为绘制顶部周界而准备，而最终底部周界应为多段线，因此就存在样条曲线转换多段线的问题。在AutoCAD 中没有提供多段线、三维多段线、样条曲线等不同线图元之间转换命令，但提供了所有线图元的定数等分（divide）和定距等分（measure）命令，通过程序编制借助定距等分命令，将样条曲线按指定间距及标高自动生成多段线，形成境界底部周界。一般底部周界多段线拐点密度取3～5 m。

在绘制顶部周界之前需要首先进行底部周界平行线的绘制，即绘制顶部周界的基础是底部周界的样条曲线。根据境界底部和顶部标高以及境界边坡角可以计算放平行线间距，在高差不变情况下，不同边坡角区域所放平行线间距也不同。对新生成的样条曲线按底部周界绘制方法，生成顶部周界多段线，然后截取本分区内的线段。一般顶部周界多段线拐点密度取3～5 m。

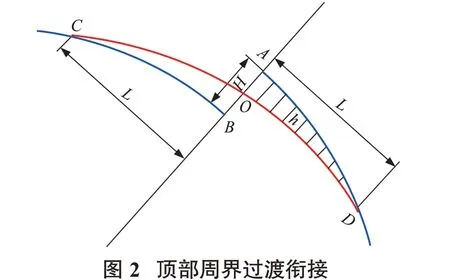
接着就是顶部周界过渡衔接，如上所述，通过底部周界放平行线获得多条顶部周界多段线，相邻线之间需要平滑过渡衔接才能形成顶部周界，如图2所示。解决此问题思路：首先计算A、B两端点间距H值及中点O位置；然后选取适当的L/H比值计算出L值，找到C、D点位置；最后通过比例插值计算出AD及BC线段中各个拐点的h 值，再将拐点坐标重新定位，完成2 条线的过渡衔接。将放平行线与过渡衔接技术组合在一起，即完成了露天矿台阶“仿平行线”放线问题。

1.3 一次境界台阶位置境界线绘制

采用顶部周界绘制方式完全可以获得任意台阶位置的境界线，但选取满意L/H 比值往往需要多次调试，不能实现2 条线自动过渡衔接，因此采用上述方法获得各个台阶境界线将会产生很大的工作量。为此，解决此问题思路：首先依据顶部周界与底部周界，采用控制线技术构建出一次境界DTM 曲面，然后采用DTM 曲面切割技术，一次性自动获取所有台阶位置境界线。

控制线组网技术旨在采用控制线将空间中2 个闭合曲线分解成多组两两对应的空间多段线，再采用空间中2 条多段线组网技术完成多组多段线的组网。如图3 所示，通过3 条控制线（A1A2，B1B2，C1C2）将2 条闭合曲线分解成3 组两两对应的空间多段线，分别是多段线A1B1与多段线A2B2、多段线B1C1与多段线B2C2、多段线 C1A1与多段线 C2A2。

空间中1条多段线组网有很多方法，最常见的是最短对角线法。如图4 所示，空间中2 条多段线A 和B 组网，首先以A1和B1作为起始三角形的2 个顶点，然后比较线段A1B2与线段B1A2长度，线段B1A2长度小于线段A1B2长度，则选择A2为三角形第三个顶点建立三角形（顶点为A1，B1，A2），再以线段 B1A2的2 个端点作为起始三角形的2 个顶点，比较线段A2B2与线段B1A3长度，选择长度小的线段A2B2，建立新的三角形（顶点为B1，A2，B2），以此类推，直至最后组网结束。

境界DTM 曲面构建依据控制线将境界底部周界与顶部周界联系在一起，采用空间2条线组网技术完成境界DTM 曲面构建，如图5 所示。通过控制线将境界底部周界与顶部周界分成上下2 组对应线段，2组对应线段采用最短对角线法分别完成各自组网。与单底境界构建技术一致，通过控制线技术分步构建出多底境界DTM曲面。

1.4 由境界DTM曲面生成台阶位置境界线

如上所述，境界DTM 曲面是由无数将境界顶部周界与顶部周界连接在一起的三角面组成。此三角形特点是其中1 条边与顶部周界（或底部周界）中的线段重合，另外2 条边则连接顶部周界与底部周界。依据台阶标高计算出三角面与标高水平面的交线，再将所有交线连接在一起形成台阶位置境界线。循环重复上面操作，可以一次性自动切割出所有台阶位置境界线。绘制台阶位置境界线实质是建立等高线的过程。

由三角面绘制等高线段，如图6 所示，已知三角面3 个顶点坐标分别为P1（x1,y1,z1），P2（x2,y2,z2），P3（x3,y3,z3），求标高z位置等高线段端点A（xɑ,yɑ,z）和B（xb,yb,z）的坐标。其中：z1为顶部周界标高，z2为底部周界标高，z为台阶位置标高，即AB线段标高。

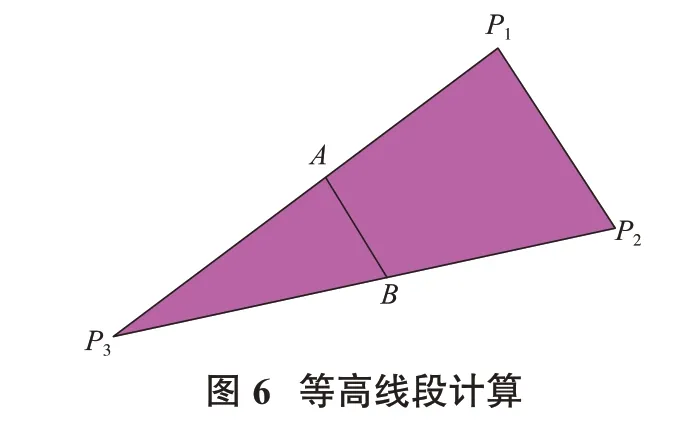
A点坐标计算：

B点坐标计算：

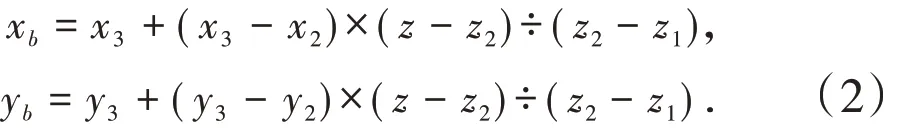
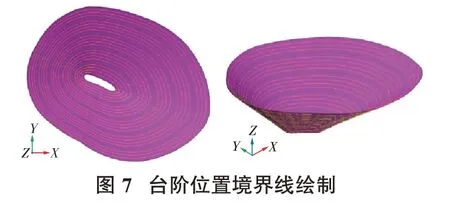
当所有三角面完成某标高交线计算后，会形成无数条等高线段，将所有线段连接在一起形成等高线，即台阶位置境界线。首先建立以坐标点为数组元素的双向链表，任选1 个等高线段放入链表，链表首端为线段的起点，链表尾端为线段的终点。接下来搜索所有链表以外的线段，如果线段某一端点与链表端点重合，则链表中加入此线段，链表端点变为线段的另一个端点，直到链表不再增加（或链表首、尾端点重复）为止，形成了1 条完整等高线。循环往复，直到等高线段集合中所有线段都进行了线段连接，最终会自动形成1 条或多条等高线，如图7 所示。

2 矿区现状DTM地表模型构建

2.1 Delaunay三角剖分算法

Delaunay三角剖分具有最小角最大化特性，使得剖分结果是最接近于规则化的三角网，同时三角网还具有唯一性（任意4 点不能共圆）。因此，Delaunay三角剖分被认为是最理想的构筑三角网方法。Delaunay 三角剖分算法包括逐点插入法、生长法、分治法、随机增量法、扫描线法等，最经典的是逐点插入法，该算法思路简单，易于编程实现，其基本原理：首先虚拟构建1个超级三角形，所有离散点均在该三角形内，然后逐一插入离散点，每插入1 个点都进行空外接圆检查，同时采用LOP 局部优化过程进行优化，直至所有离散点插入完成，最后删除与超级三角形顶点相关的所有三角形。

当离散点数目适中时，逐点插入法是不错的选择，从构筑三角网过程可知，该方法构网算法理论严密、唯一性好，三角网满足空外接圆特性，较为理想。因此该方法适合露天矿地表模型构建。

2.2 地形线重复、骑跨、交叉快速检测

由于在露天矿境界设计时，无论原始地表模型或是终了境界模型，其基础数据都是三维地形线。因此，此类三角网构筑属于有约束三角剖分，即地形线与三角形的边完全重合。

对于有约束三角剖分，要求地形线不许出现重复、骑跨、交叉等情形，因此，在构筑三角网之前要进行基础数据检测，将不符合条件的地形线找出并修正。由于地形线的数据较多，无法用肉眼识别错误，应采用程序进行快速检测。

地形线不准许重复、骑跨、交叉等情形与离散点数目不是特别多时，逐点插入法较合适。从构筑三角网过程可知，该方法构网算法理论严密、唯一性好，三角网满足空心圆特性，较为理想，该方法适合露天矿地表模型构建。

线段检测方法：假设线段L1的端点为A 和B，线段L2的端点为C 和D，如果端点A 和B 分别在线段L2两侧，同时端点C 和D 分别在线段L1两侧，则线段L1与线段L2骑跨或交叉；如果端点A 和B 都与线段L2共线，且线段L1与线段L2有交集，则线段L1与线段L2重合（局部重合或完全重合）。

2.3 DTM地表模型构建

如前所述，DTM 地表模型构建属于有约束三角剖分，首先提取所有地形线拐点，组成离散点集合，然后采用逐点插入法进行Delaunay三角剖分，构筑出初始三角网，最后分解地形线组成线段集，并逐个线段进行检验，当线段骑跨多个三角形时，删除骑跨三角形重新完成局部三角剖分，直至所有线段检验结束，DTM 地表模型构建完成。在构建DTM 地表模型中，需要构建点集合、线段集合、三角形集合和三角形顶点与边的对应关系。

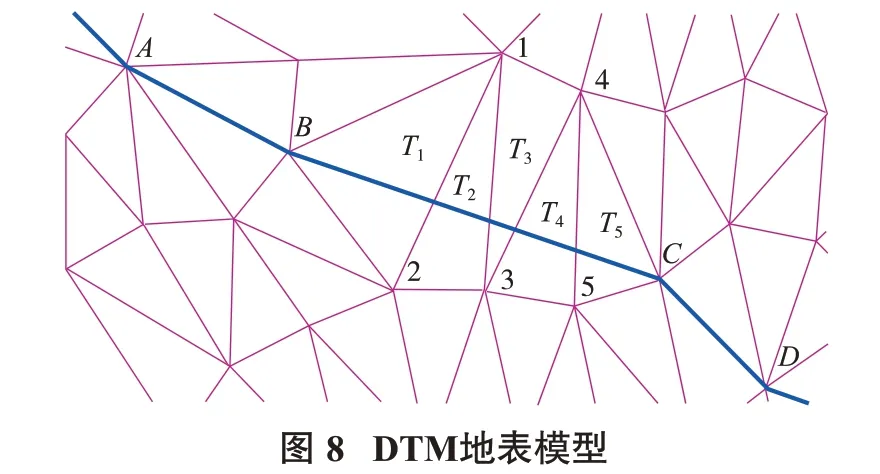
有以上拓扑关系可以看出，主要以点作为纽带，通过点可以找到与点对应的所有对应边及所在三角形。当采用Delaunay三角剖分构建出初始三角网后，即可形成上述拓扑关系数据。在做约束线段检查时，首先根据线段起点标号找到包含此点的所有三角形，以及其对应边。判断约束线段与对应边的关系，如果约束线段终点与对应边某个端点重合，则约束线段是三角形的边，满足要求不做处理；如果与对应边骑跨，则此三角形为骑跨三角形，进一步判断对应边2 个端点的对应边与约束线段关系，如此往复，找出所有骑跨三角形。如图8 所示，线段AB 和CD 与三角形边重合，满足要求不做处理。线段BC 骑跨三角形T1～T5，删除所有骑跨三角形，线段在BC 分别与左侧多段线（B，1，4，C）、右侧多段线（B，2，3，5，C）重新组网，并修正三角网拓扑关系。

3 工程实例

蒙库铁矿床位于阿勒泰市南东75 km 处，矿区总长10 km，宽1 km，面积为20 km2；工作区长4 000 m，宽500 m，面积为2 km2，属新疆维吾尔自治区富蕴县管辖。矿区交通比较方便，由阿勒泰市、北屯镇、富蕴县均有公路通达矿区，其中由富蕴县至蒙库铁矿的公路可通行重型运输卡车，路程为100 km。

蒙库铁矿中段矿体形态简单，厚度较大，大面积出露地表，因此该矿床推荐露天开采。设计根据境界剥采比小于经济合理剥采比原则，圈定了露天矿的开采境界。设计台阶坡面角为70°，本次设计最终境界台阶高度为10 m，出入沟宽度为9 m，每布置2个安全平台就布置1个清扫平台，安全平台宽5 m，清扫平台宽10 m；露天矿最小底宽为22 m；露天矿上盘最终坡面角为42°；下盘最终坡面角为43°；采场最大长度为1 105 m，最大宽度为606 m，最终开采底部标高为920 m，开采深度最深为330 m。

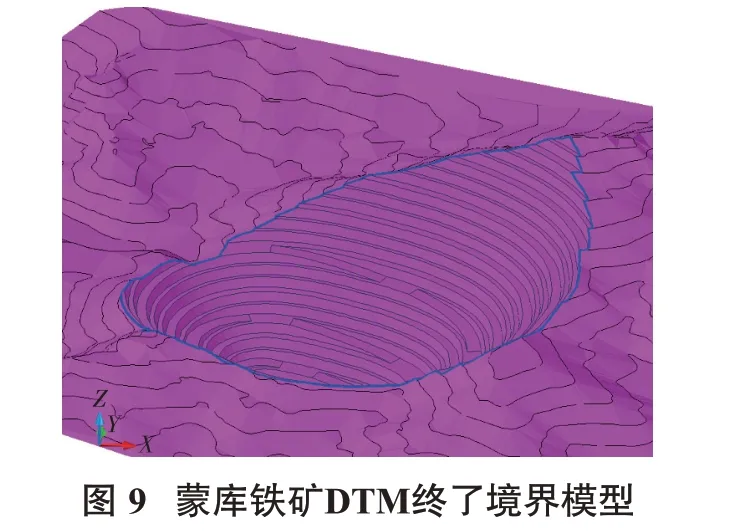
依据露天矿终了境界设计的原则，在Auto CAD平台下开发一次境界DTM 曲面快速构建和曲面剪切运算模块，最终完成蒙库铁矿终了境界图的绘制，见图9。