胶印配色光学常数求解方法优化

史太川 吕 伟

深圳劲嘉集团股份有限公司 广东 深圳 518105

0 引言

越来越多的印刷企业采用计算机配色软件进行专色油墨配色，以提高配色的准确性与效率。计算机配色的关键是建立准确的、与模型相匹配的配色基础数据库。大部分配色模型是以Kubelka-Munk理论（K-M理论）为依据[1]。构建基于K-M单常数理论配色模型的基础数据库时，配色光学常数（吸收系数K和散射系数S）的求解会直接影响配色效率、颜色预测精度。目前，基墨配色光学常数求解方法主要有基墨色调阶梯法和数学算法[2]。

基墨色调阶梯法是将制备于不透明基底上的基墨纯色样本的光谱反射率R代入K-M理论简化方程即K/S=(1-R)2/(2R)，或将制备于透明薄膜（假设透射率为1）的基墨纯色样本分别背衬黑白的光谱反射率R、R0及白背衬的光谱反射率Rg代入公式[3-4]a=1+K/S=1/2[R+(R0-R+Rg)/(R0Rg)]，求得基墨光学常数。但多数纯色基墨光吸收能力强、反射率相较不高，导致基墨光学常数求解结果误差较大。Cairns色调阶梯法[5]通过制备多组不同质量配比的基墨与冲淡剂混合样本，使用最小二乘法[6-7]求解基墨光学常数。因基墨混合样本的质量配比与吸收散射比的关系用Duncan色料混合光学模型的线性加和定律描述不准确，故常选取8～12个色调阶梯[8-9]，以降低各质量配比所求光学常数的差异对配色精度的影响。此外，根据样本配比与吸收散射比的关系曲线，可选取少量曲线特征点求解光学常数，但目前特征点的选取并无量化依据[10]。

数学算法是对线性显著的低配比段进行线性内插求解光学常数[11]，或将各配比段所求光学常数的均值代入非线性拟合关系函数得到初步配比，再对初步配比的相邻两基准配比段的光学常数进行内插，得到接近实际的光学常数[12]。前者预测精度不高，后者仅理论上成立。两种算法得到的光学常数难以综合表征基墨在质量配比范围内的光学特性。此外，随着质量配比的增加，曲线振荡越大[13]。

针对基墨色调阶梯法中色调阶梯选取不当、建库工作量大等问题，本研究拟先分析胶印配色数据库中基墨混合样本的质量配比与吸收散射比的关系，再用两种色调阶梯法选取色调阶梯，缩减制样数量，提高配色建库效率。

1 K-M单常数理论和光学常数求解

1.1 K-M单常数理论

K-M单常数理论由K-M理论和色料线性加和定律组成。任一波长处，混合色料膜层的吸收系数K与散射系数S适用线性加和定律，即将各单组份色料光谱间复杂的非线性关系转换为吸收与散射系数间简单的线性关系（见公式（1））。若色料混合介质膜层不透明，通过Saunderson修正[4]光谱反射率，再求吸收散射比。

部分情况下（如印刷呈色），色料以分子形态附着于基底表面，其尺寸远小于可见光波长，故其对光的散射作用可忽略不计。基于此，色料配比变化对S影响不大，S可视为基底散射系数。将记为，式（1）可简化为

1.2 光学常数

基于K-M单常数理论的光谱配色模型中，光学常数即为单组份基墨的吸收散射比。多数纯色基墨的光吸收能力强、反射率相对不高，导致光学常数的求解结果误差较大。为解决此问题，将基墨与冲淡剂混合以减弱纯色基墨的光吸收能力。已知混合样本的基底在波长λ处的吸收散射比，则混合样本的吸收散射比为

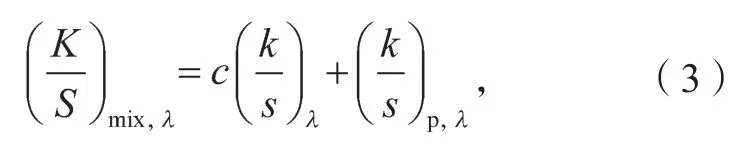
式中：c为基墨质量配比；为单组份基墨在波长λ处的吸收散射比。

通过单个混合样本求解光学常数，易受制备工艺误差影响，且混合样本的配比与吸收散射比并非理想线性关系。因皮，根据式（3），利用多组不同配比的混合样本联立方程组求解光学常数，即

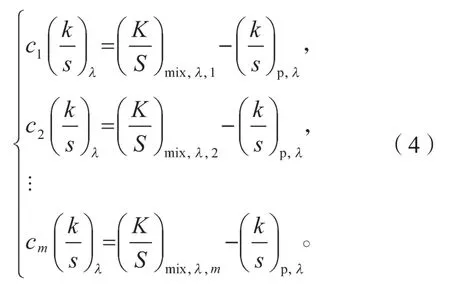
式中：m为混合样本个数；cm为第m个混合样本的基墨质量配比；为第m个混合样本在波长λ处的吸收散射比；为混合样本的基底在波长λ处的吸收散射比。

式（4）为多个方程对应一个未知变量（单组份基墨吸收散射比）的超定方程组，故可通过线性最小二乘法求解。

令

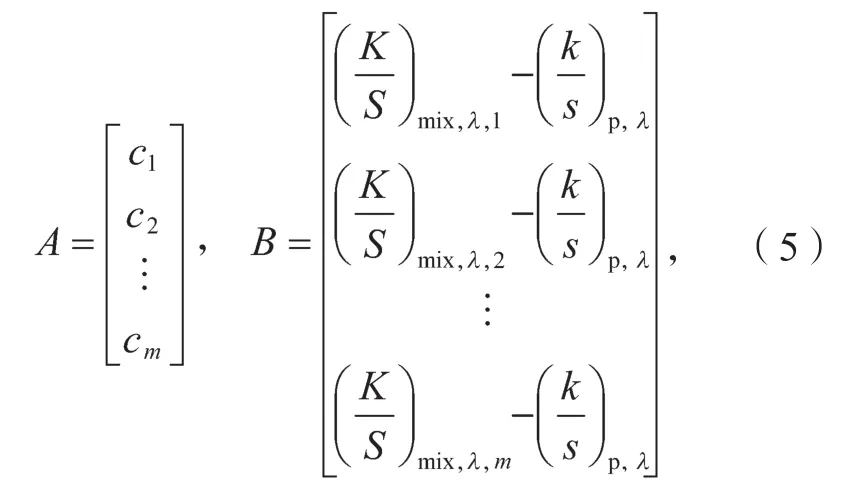
则波长λ处单组份基墨的吸收散射比为

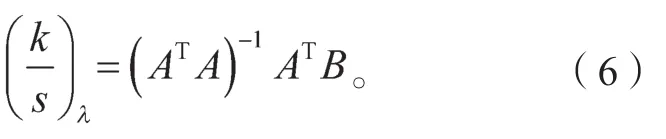
2 色调阶梯实验

2.1 混合样本制备及其光谱获取

混合样本中胶印基墨的质量配比为5%～100%，间隔为5%，即为基础配比。实验均在恒温恒湿环境（温度为22～24 ℃；相对湿度为50%～55%）下进行，承印物为金太阳定量200 g/m2单面涂布白卡纸，无荧光效果；基墨为盛威科耐折系列黄（Y）、红（M）、蓝（C）、黑（K）。实验主要仪器如表1所示。

表1 实验仪器Table 1 Experimental apparatus

在不同的打样速度、打样压力及上墨量下，用印刷适性仪打印黑色样张。经密度测量，得到当打样条件为：打样速度0.2 m/s、打样压力500 N、上墨量0.08 g时，黑色样张的密度能达到胶印实地密度控制标准，且与胶印印张基色黑色标密度匹配。故不同浓度梯度的基墨混合样本均是在此打样条件下制备，如图1所示。

图1 印刷样张Fig. 1 Printing proofs

彩图

为确保基墨混合样本光谱反射率的测量结果有效，测量时采用自体背衬（若干张相同白卡纸）[14]。以一半的印刷样张为例，其光谱反射率如图2所示。

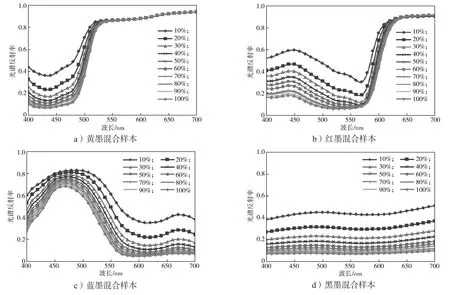
图2 印张光谱反射率Fig. 2 Spectral reflectivity of printing proofs

彩图

2.2 样本配比与吸收散射比的关系

用Saunderson修正光谱反射率后，利用公式（1）得到基墨混合样本及基底的吸收散射比，并利用公式（3）得到单组份基墨混合样本的吸收散射比。以混合样本中半数为例，通过线性最小二乘法求解单组份基墨吸收散射比，并将其进行极差归一化变换，结果如图3所示。

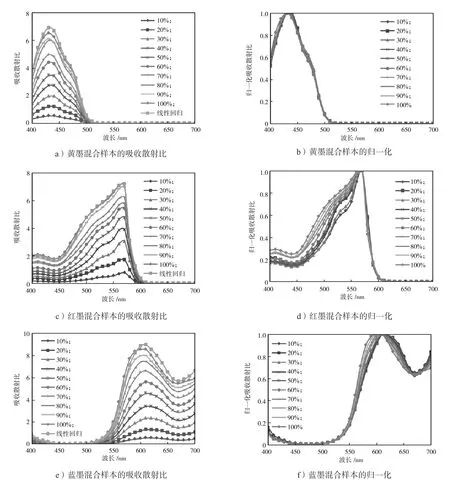
图3 印张吸收散射比与其归一化图Fig. 3 The absorption and scattering ratios of printing proofs and its normalization

彩图

由图3可以看出，随波长的增加，各基墨混合样本的吸收散射比与光谱反射率的变化趋势相反。理论上，任一质量配比的基墨混合样本中单组份基墨散射吸收比应相同，但实际却存在一定偏差；基墨混合样本吸收散射比归一化后的曲线应完全重合，但实际上除黄墨混合样本外，其他三种基墨混合样本的归一化曲线并未完全重合，亦即吸收散射比与质量配比呈非线性关系。因此，选择合适的质量配比基墨混合样本是提高配色模型光谱预测精度的关键。

2.3 求解光学常数的样本数量优化

基墨混合样本的吸收散射比峰值与光谱反射率谷值相对应，此处波长对基墨混合样本吸收散射性能的影响较大，故称之为主吸收波长。因此，本研究分析主吸收波长处基墨混合样本的质量配比与吸收散射比的关系。

将主吸收波长处基墨混合样本的质量配比与吸收散射比进行非线性最小二乘法拟合，即

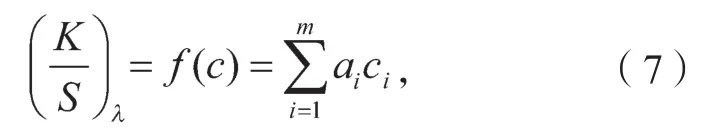
式中：ai为待定系数，具体数值见表2；m为多项式最高次数，m=3。

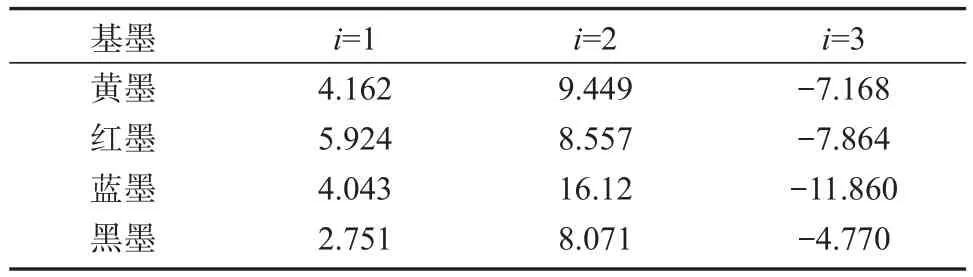
表2 4种基墨混合样本的多项式拟合系数aiTable 2 Polynomial fitting coefficient ai of 4 based ink mixed samples

拟合结果见表3。由表可知，和方差（sum of squares for error，SSE）与均方根误差（root mean square error，RMSE）皆接近0，决定系数（R-square，R2）与校正决定系数（adjustedR-square）皆接近1。可见，当m=3时，4种基墨混合样本的拟合优度最佳。

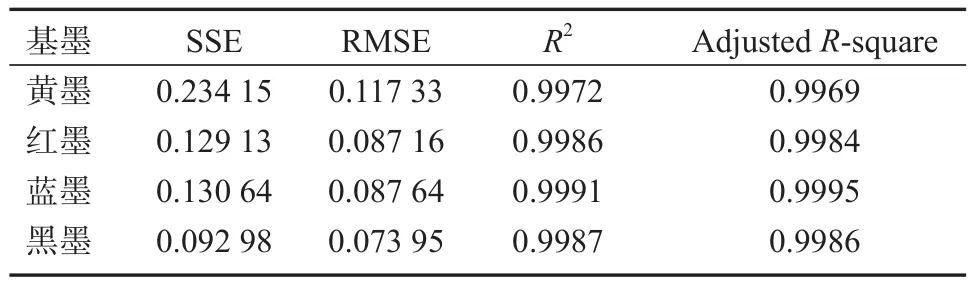
表3 4种基墨混合样本的多项式拟合优度Table 3 Polynomial goodness of fit of 4 based ink mixed samples

分别用线性最小二乘法和非线性最小二乘法对主吸收波长处基墨混合样本的质量配比与吸收散射比进行拟合，结果如图4所示。

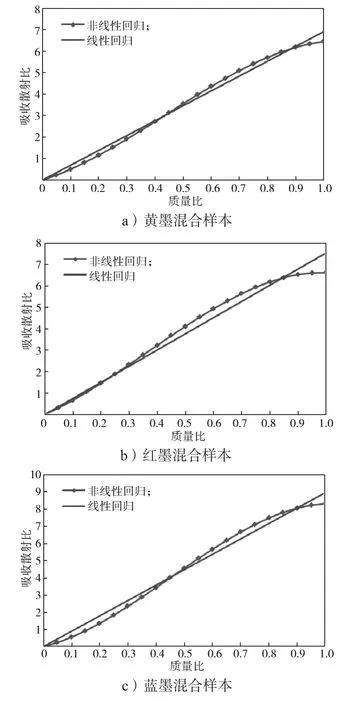
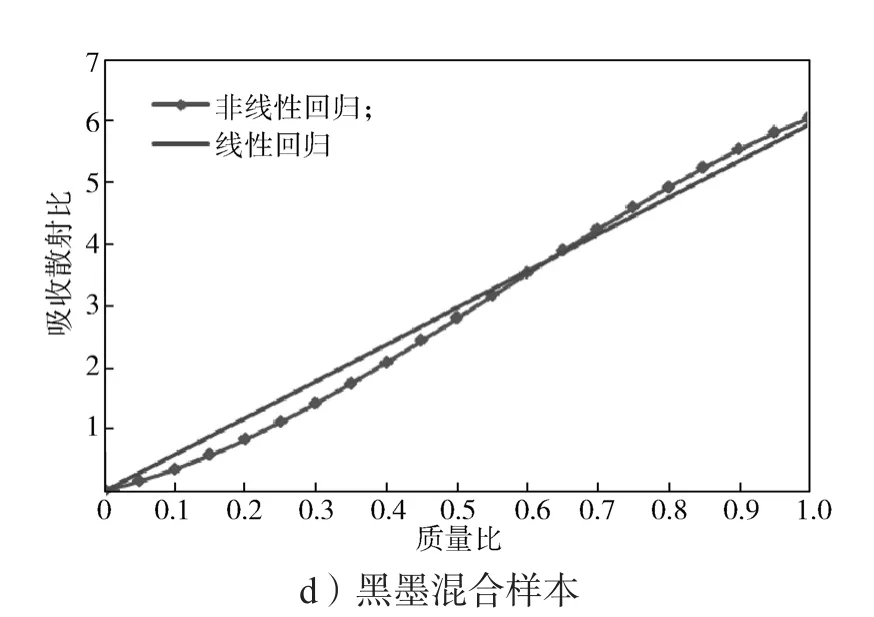
图4 4种基墨混合样本的拟合结果图Fig. 4 Fitting result of 4 based ink mixed samples

图4中，黄墨、红墨、蓝墨、黑墨的线性回归直线斜率分别为其在主吸收波长处的吸收散射比，即6.91, 7.54, 8.96, 5.95。因去除了基底光学特性，故线性回归直线过坐标原点。用线性回归直线与非线性回归曲线交点处的质量配比求解光学常数，此配色模型的光谱预测精度最好。因而求解光学常数的质量配比只需1～2个。但实际上，若仅选1～2个质量配比求解光学常数，则样本制备工艺误差易导致光学常数求解不准，故需增加求解光学常数的质量配比数量。在保证正反向预测模型精度前提下，本研究提出用一阶导和误差排序两种色调阶梯法分别优化求解光学常数的质量配比数量。

1）一阶导色调阶梯法

基墨混合样本的线性回归直线与非线性回归曲线的位置关系（见图4）符合拉格朗日中值定理几何意义，故求式（7）一阶导数（见式（8）），并选取一阶导数与线性回归直线斜率最接近的两个质量配比及其左右相邻的质量配比各1（见表4）。各基墨混合样本均选取6个质量配比，用带约束的线性最小二乘法求解单组份基墨吸收散射比。

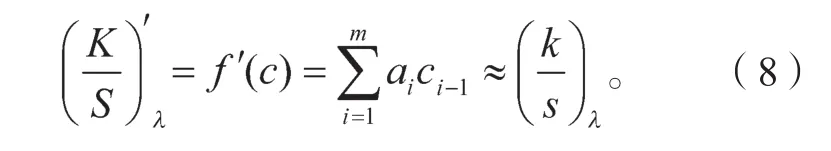
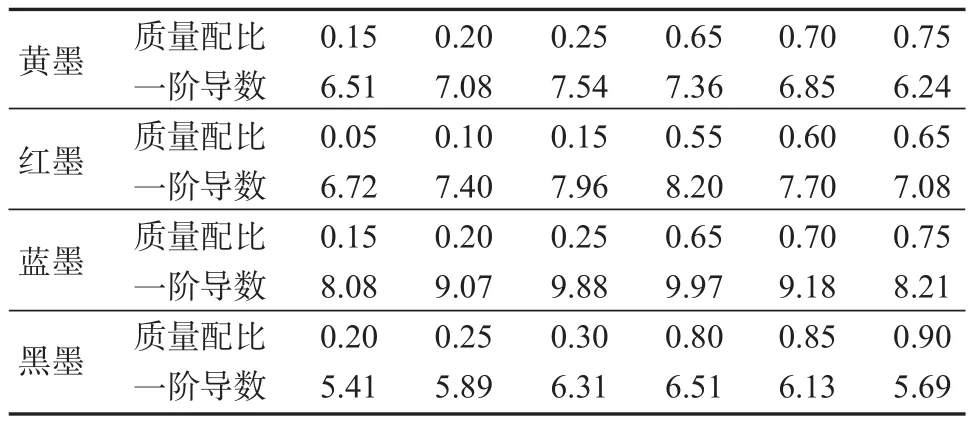
表4 基墨混合样本非线性回归曲线的一阶导数表Table 4 First derivative of nonlinear regression curve of based ink mixed samples

2）误差排序色调阶梯法

计算基墨混合样本在线性回归直线与非线性回归曲线中同一质量配比对应的吸收散射比绝对误差，并将其从小到大进行排序。综合来看，各基墨混合样本的较小绝对误差值主要位于较小质量配比、中等质量配比及较大质量配比处。为降低样本制备工艺误差的影响，进一步选取与此3种质量配比差异最小的配比各1个，则每种基墨各选出绝对误差较小的前6个质量配比（见表5）。将6个质量配比进行带约束的线性最小二乘法拟合，求解单组份基墨吸收散射比。

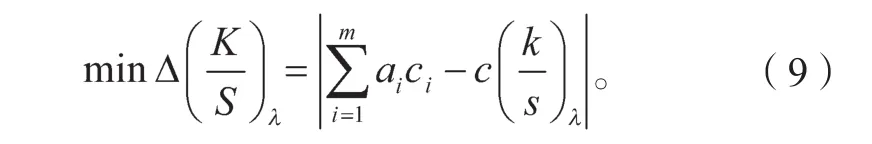
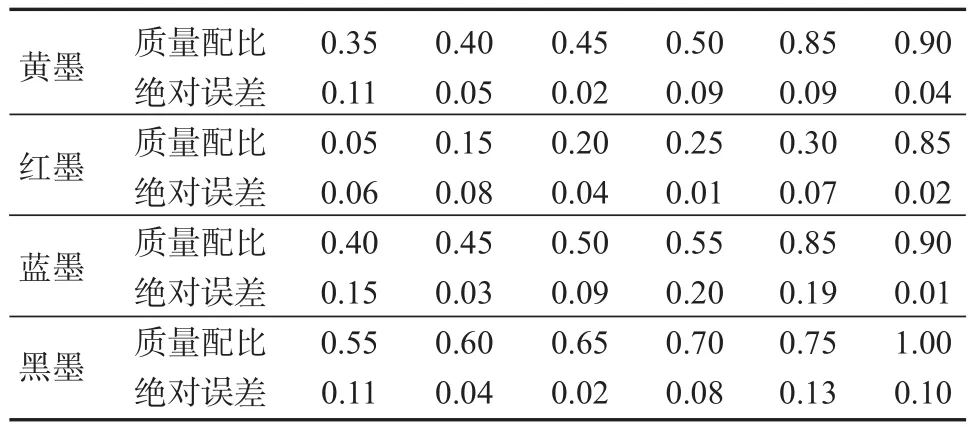
表5 基墨混合样本线性与非线性回归曲线的绝对误差表Table 5 Absolute error of linear and nonlinear regression curve of based ink mixed samples

3 结果与分析

3.1 光学常数

为验证一阶导色调阶梯法与误差排序色调阶梯法的合理性与准确性，将色调阶梯法与混合样本基础配比分别得到的单组份基墨吸收散射比进行比较，如5图所示。

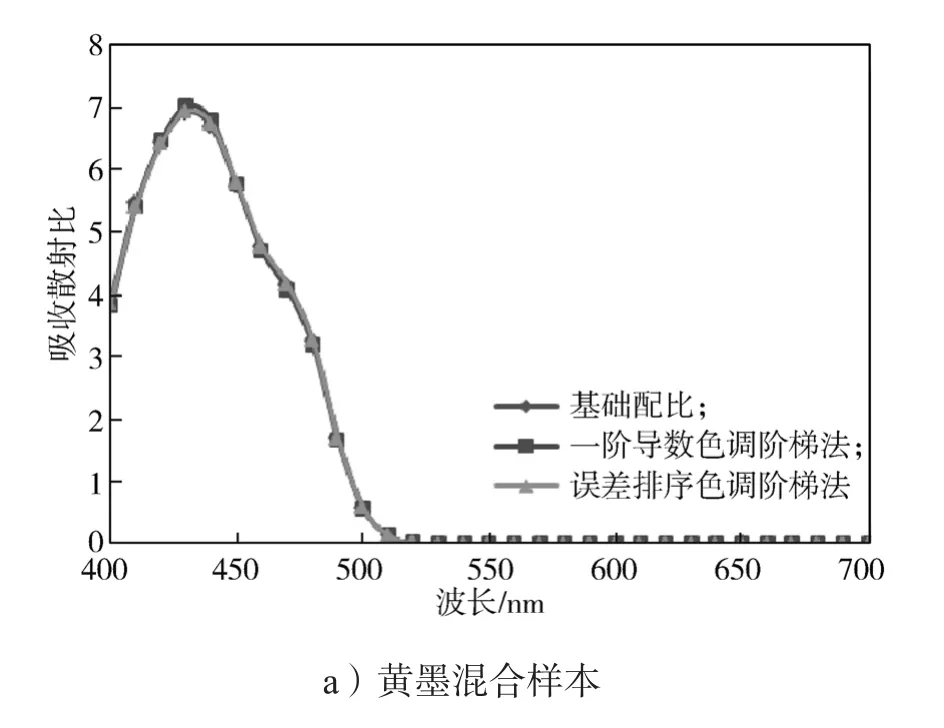
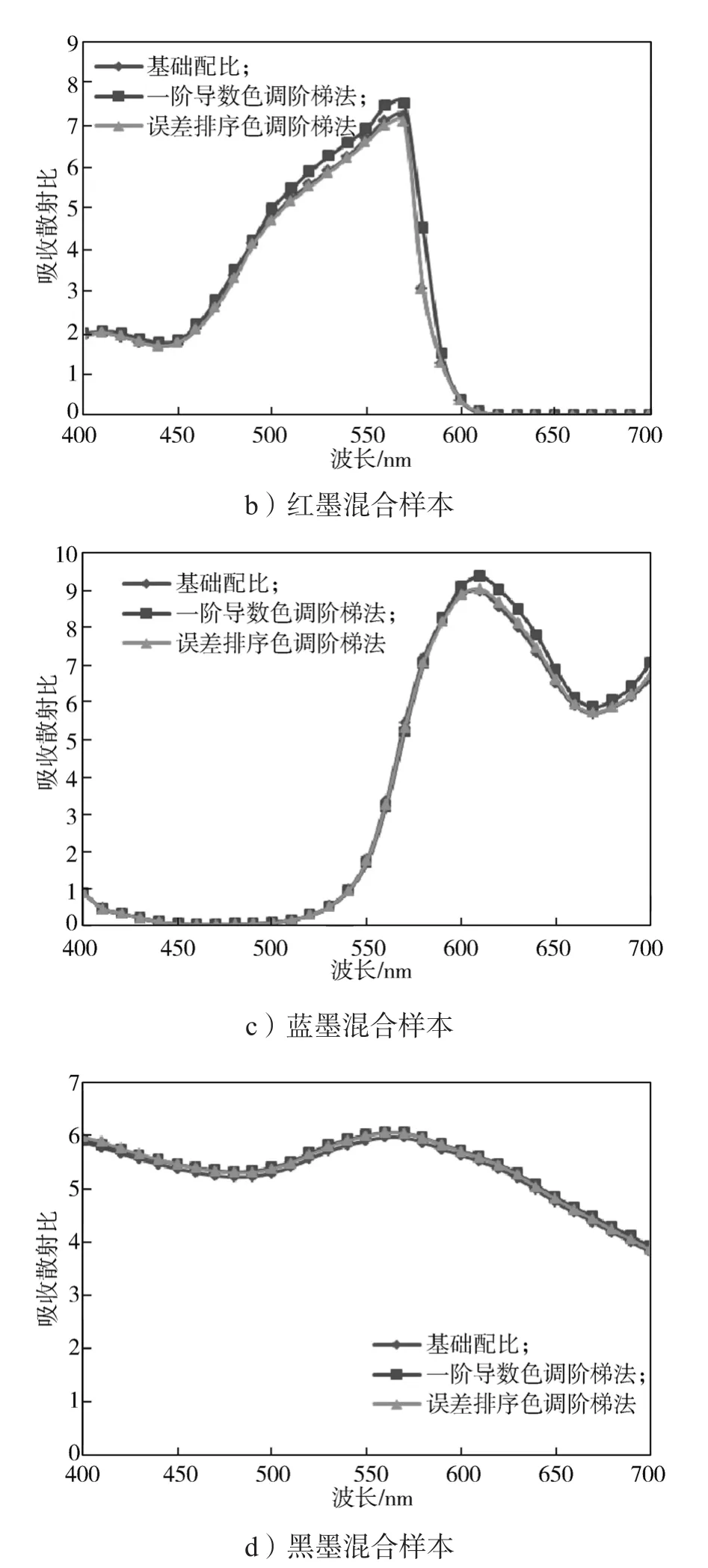
图5 3种方法所得吸收散射比比较Fig. 5 Comparison of the absorption and scattering ratios calculated by 3 methods

从图5可以看出，各波长处黄墨和黑墨混合样本由色调阶梯法得到的单组份基墨吸收散射比均与基础配比得到的单组份基墨吸收散射比较为接近；而对于红墨和蓝墨混合样本而言，在主吸收波长附近，用误差排序色调阶梯法得到的单组份基墨吸收散射比与基础配比得到的单组份基墨吸收散射比更接近，但两种色调阶梯法求解效果的差异不显著。

3.2 颜色预测精度

根据光学常数分析结果，选取胶印印张中三拼色专咖啡与双拼色专红两个目标色（见图6）进行颜色预测精度验证分析。已知专咖啡的基墨配比m黄:m红:m黑=0.5563:0.3042:0.1395，专红的基墨配比m黄:m红=0.3356:0.6644，分别用一阶导色调阶梯法和误差排序色调阶梯法色阶求解的基墨光学常数，对两个目标色进行正向光谱预测和反向配比预测，并分析预测的配比差、光谱误差及色差。

图6 胶印印张专咖啡与专红色标Fig. 6 Brown and red spot color batches of offset printed sheet

正向光谱预测模型建立了从单组份基墨的配比到输出光谱反射率之间的预测模型，而反向配比预测模型是在已知复制光谱反射率的前提下，反向求解各单组份基墨配比。由于正向光谱预测模型通常无法求解反函数，故常视反向配比预测模型为带约束的非线性优化问题。通过带约束优化问题函数对目标函数进行迭代寻优，即寻找最小光谱匹配误差。目标函数为预测光谱rpre与目标色混合样本光谱rtar的误差，即

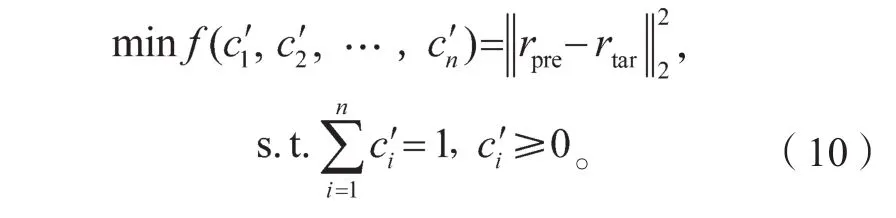
分别用一阶导色调阶梯法、误差排序色调阶梯法的光学常数预测目标色，并与基础配比的光学常数预测目标色的结果进行比较，配比差（欧几里得距离）、光谱误差（RMSE）及色差（D65/2°条件下ΔEab）如表6所示。

表6 两种色调阶梯法的预测结果Table 6 Predictions of two tint ladder methods

由表6可知，一阶导色调阶梯法、误差排序色调阶梯法及基础配比混合样本的光学常数对专咖啡的预测，在配比差、光谱误差及色差上均差异不大；三者对专红的预测，光谱误差与色差差异不大，但一阶导色调阶梯法的配比差明显大于另外二者。

3种配比样本光学常数对两个目标色的预测光谱如图7所示。

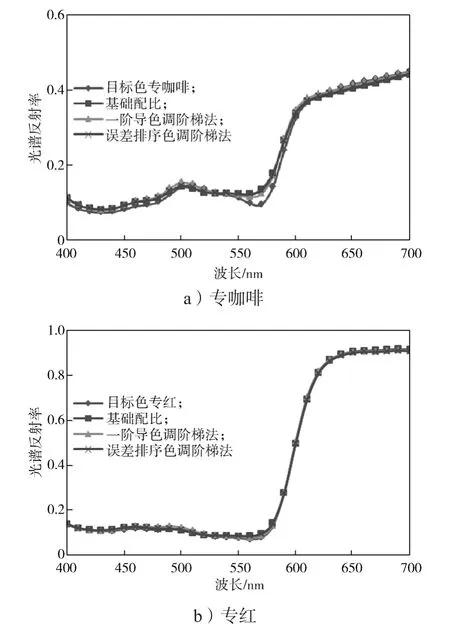
图7 3种配比样本光学常数的预测光谱与目标色光谱图Fig. 7 Prediction spectrum of the 3 ratio samples optical constants and target color spectrum

由图7可知，一阶导色调阶梯法、误差排序色调阶梯法及基础配比混合样本的光学常数对专咖啡的预测光谱较接近，但与目标色光谱存在一定偏差；三者对专红的预测光谱也较接近，且与目标色光谱较为吻合。

4 结论

为构建基于K-M单常数理论的胶印配色数据库，本研究选取胶印基墨与冲淡剂混合样本，基墨质量配比在5%～100%之间，间隔为5%，对基墨质量配比与吸收散射比之间的关系进行理论与实验分析，并提出了一阶导和误差排序两种色调阶梯法，以选择适量的质量配比求解光学常数。通过基础配比混合样本、一阶导色调阶梯法及误差排序色调阶梯法建立的数据库进行颜色预测，结果表明：两种色调阶梯法的颜色预测精度（最大光谱误差为0.0137，最大色差为1.73）均满足实际生产应用需求。可见，本研究所提配色光学常数求解法可在保证颜色预测精度前提下，提高配色数据库建立效率，对印刷包装企业应用计算机配色具有一定指导意义。