Stewart式六维力传感器轻量化设计
2022-09-13王晨,高波,杨旭
王 晨,高 波,杨 旭
(1.陕西工业职业技术学院航空工程学院,陕西 咸阳 712000;2.中国航天科技集团公司陕西电器研究所,陕西 西安 710065;3.北京空间飞行器总体设计部,北京 100094)
六维力传感器能实现对空间力学环境的实时监控,有效地解决空间复合力测量问题。常见的六维力传感器按结构可分为Stewart式和一体式。其中,Stewart式六维力传感器具有量程大、精度高和质量小等优点,被广泛应用于航空航天领域。
2003年,燕山大学的赵现朝[1]对Stewart式六维力传感器的性能指标定义、样机设计及静力标定等进行了详细研究。2008年,浙江大学的王宣银等[2]提出了一种新型的Stewart式六维力传感器标定方法。2009年,燕山大学的姚建涛等[3]设计了一种大量程预紧式六维力传感器。2017年,陕西电器研究所的刘晓宇等[4]、高波等[5]设计了一款基于局部去耦的重载型Stewart式六维力传感器。然而,目前针对Stewart式六维力传感器的研究主要集中在其精度、各同向性等方面[6-9],虽有关于其质量方面的理论分析,但缺乏工程应用层面的研究。
鉴于高强度、轻量化为航空航天设备的重要技术目标,笔者拟通过理论推导、数值仿真及实验验证相结合的方式,在满足Stewart式六维力传感器灵敏度和刚度要求的基础上,设计一种新型的减重结构,以实现其轻量化设计。
1 Stewart式六维力传感器各向同性优化设计
Stewart式六维力传感器是由上、下加载盘和6个支路传感器(通常每个支路传感器均看作“二力杆”)组成的装配体。其中,上、下加载盘为主要支撑部件,支路传感器为弹性敏感元件。如图1所示,决定Stewart式六维力传感器性能的主要参数为支路传感器与上、下加载盘的铰接点到对应加载盘中心的距离R2、R1,支路传感器在上、下加载盘上的定位角φ2、φ1以及上、下加载盘中心之间的距离Hc[10-12]。图中:ui、Ui(i=1,2,…,6)为各支路传感器与上、下加载盘的铰接点。
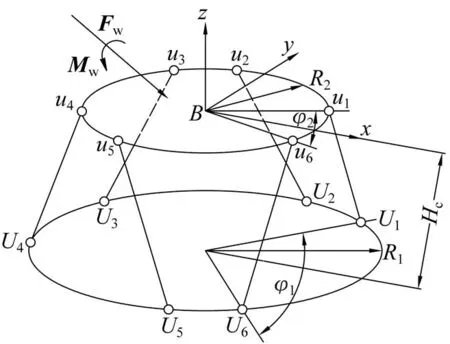
图1 Stewart式六维力传感器结构简图Fig.1 Structural diagram of Stewart type six-axis force sensor
根据螺旋理论,建立各支路传感器的轴向力与作用于上加载盘中心的力和力矩的平衡方程:
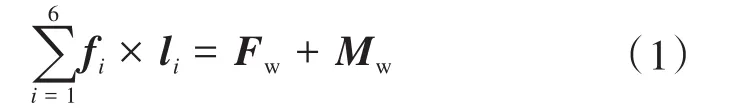
式中:fi为第i个支路传感器的轴向力;li为第i个支路传感器轴线指向坐标系原点(以上加载盘中心为原点构建坐标系)的单位矢量;Fw、Mw分别为作用于上加载盘中心的力和力矩,
将式(1)简化为矩阵形式,可表示为:

式中:F为广义外力矢,F=[FwMw];G为Stewart式六维力传感器的一阶静力影响系数矩阵;f为支路传感器反作用力矩阵。
研究表明,Stewart式六维力传感器的一阶静力影响系数矩阵G仅与其结构参数R2、R1、φ2、φ1及Hc有关。若G非奇异,则G可逆,即有:
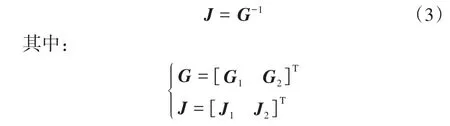
式中:J为Stewart式六维力传感器的雅克比矩阵;G1、G2和J1、J2分别为Stewart式六维力传感器的一阶力/力矩影响系数矩阵和力/力矩雅克比矩阵。
则广义外力矢F与支路传感器反作用力f的关系可表示为:

由此可得,Stewart式六维力传感器所受力/力矩的各向同性度及其灵敏度的各向同性度为:
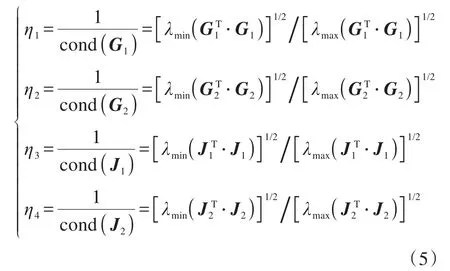
式中:η1、η2和η3、η4分别为Stewart式六维力传感器所受力/力矩的各向同性度及其灵敏度的各向同性度。
以Stewart式六维力传感器所受力/力矩的各向同性度及其灵敏度的各向同性度为主要参数,建立其综合性能目标函数:
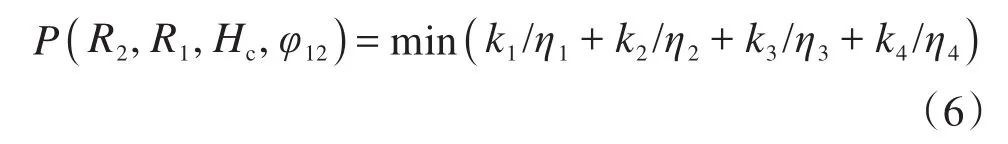
式中:k1、k2和k3、k4分别为力/力矩的各向同性度η1、η2及其灵敏度的各向同性度η3、η4的权重系数,权重矩阵k=[k1k2k3k4];φ12为支路传感器在上、下加载盘上的定位角之差。
结合式(7)所示的Stewart式六维力传感器各结构参数的约束条件,利用MATLAB工具箱对所构建的综合性能目标函数[13]进行优化求解,得到该传感器各向同性度理论最优时的结构参数。

表1所示为Stewart式六维力传感器各向同性度理论最优时的结构参数,其理论最优各向同性度如表2所示。

表1 Stewart式六维力传感器各向同性度理论最优时的结构参数Table 1 Structural parameters of Stewart type six-axis force sensor with optimum theoretical isotropy

表2 Stewart式六维力传感器的理论最优各向同性度Table 2 Theoretical optimum isotropy of Stewart type sixaxis force sensor
根据表1所示的结构参数以及表3所示的量程,制作Stewart式六维力传感器的初始样机,其主要由上加载盘、下加载盘和支路传感器(铰座、弹性体及去耦件)组成(不计外部滤波放大组件),如图2所示。

表3 Stewart式六维力传感器量程Table 3 Range of Stewart type six-axis force sensor

图2 Stewart式六维力传感器初始样机Fig.2 Initial prototype of Stewart type six-axis force sensor
2 Stewart式六维力传感器有限元模型构建
鉴于Stewart式六维力传感器为装配体,其组件数量较多且约束关系复杂,故采用Pro/E软件建立其三维模型,并以SAT文件格式导入ABAQUS有限元分析软件。在ABAQUS软件中进行约束关系设置时,为更接近实际Stewart式六维力传感器各组件间的连接方式,采用Tie约束。
网格设置会直接影响数值仿真的可靠性。由于所设计的Stewart式六维力传感器的组件均以圆柱体或圆槽形结构为主,其尺寸为30~100 mm,为提高数值仿真的计算时效性和准确性,选取四面体二次单元C3D10M作为各组件的主要单元。对传感器整体采用自由网格划分技术,对弹性体应变测量区采用扫琼网格划分技术。上、下加载盘的材料为超硬铝7A04,支路传感器(铰座、弹性体及去耦件)的材料为钛合金TB9。为满足计算精度要求,对Stewart式六维力传感器有限元模型进行网格密度影响无关性分析,结果如图3所示。
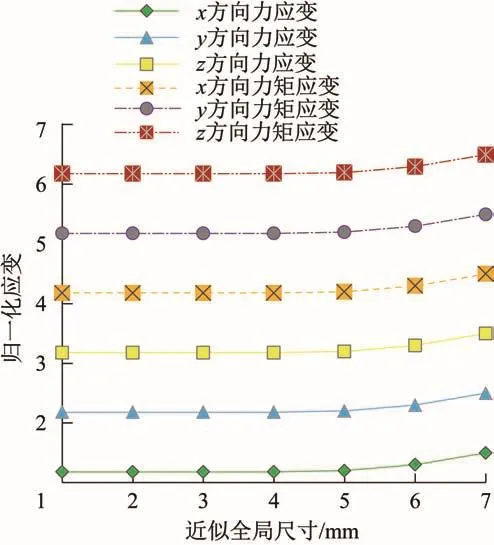
图3 Stewart式六维力传感器有限元模型的网格密度影响无关性分析结果Fig.3 Analysis results of grid density influence independence of Stewart type six-axis force sensor finite element model
由图3可知,当近似全局尺寸小于4 mm时,Stewart式六维力传感器有限元模型的计算精度不受网格密度的影响,最终共生成150万个C3D10M网格单元,划分效果如图4所示。此外,外力矢的传导是通过上、下加载盘的螺孔和销孔实现的,为更接近真实的力矢传导,采用梁约束方式进行等效,并在下加载盘的螺纹处施加固支约束,完成荷载状态设置。

图4 Stewart式六维力传感器有限元模型Fig.4 Finite element model of Stewart type six-axis force sensor
3 Stewart式六维力传感器初始样机性能分析
利用所构建的Stewart式六维力传感器有限元模型,计算其初始样机在不同工作荷载下的强度、刚度和灵敏度,同时参照设计要求对其刚度和灵敏度进行测试,对比结果如表4所示。表中:σmax为最大应力,εmax为最大应变,σeav为弹性体工作区的平均应力,KF为拉压刚度,KM为扭转刚度,T为灵敏度。值得注意的是,相同荷载工况下,上、下加载盘的应力仅为弹性体应力的7%~12%,故不计入统计。由表4可知,通过数值仿真得到的Stewart式六维力传感器初始样机的最大应力远小于材料的屈服极限1 050 MPa,无论是仿真刚度还是实测刚度均远大于设计要求,灵敏度远小于最佳灵敏度2 mV/V。
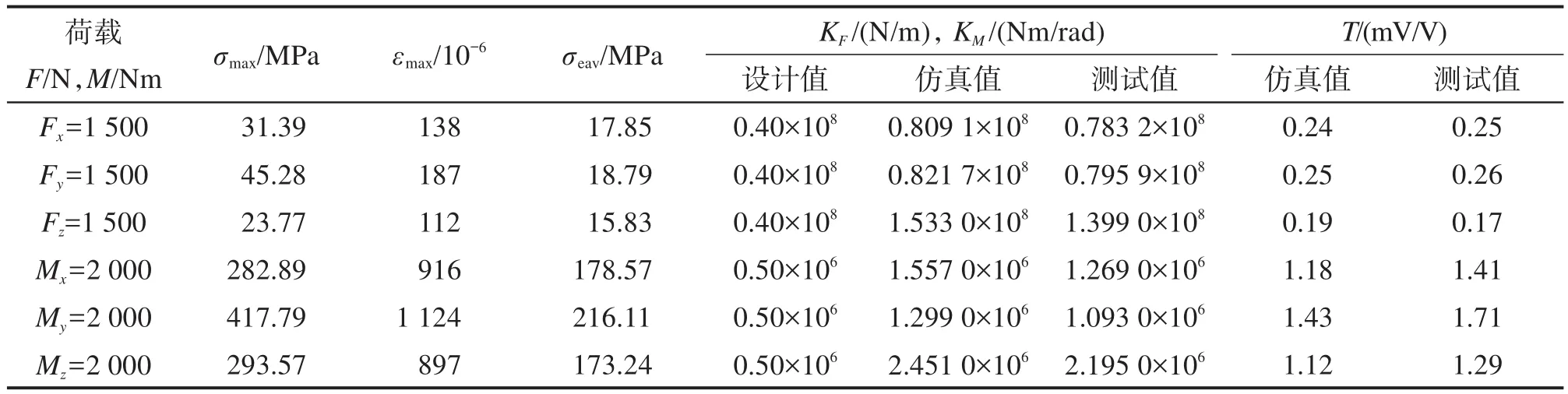
表4 Stewart式六维力传感器初始样机的性能对比Table 4 Performance comparison of initial prototype of Stewart type six-axis force sensor
经实测,Stewart式六维力传感器初始样机的质量为6.437kg,其质量分布如表5所示。由表5可知,Stewart式六维力传感器初始样机的上、下加载盘质量占总质量的77.54%,而支路传感器(铰座、弹性体及去耦件)和标准件(螺钉、螺母)的质量仅占22.46%。
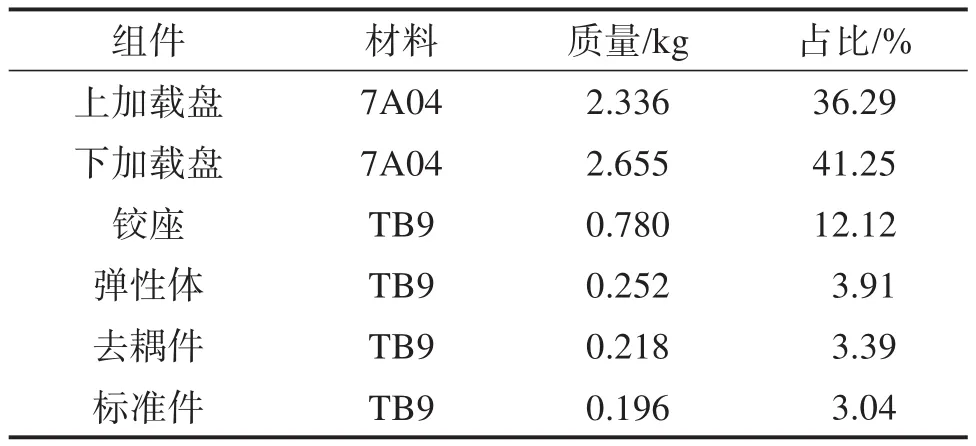
表5 Stewart式六维力传感器初始样机的质量分布Table 5 Mass distribution of initial prototype of Stewart type six-axis force sensor
综上可知,Stewart式六维力传感器初始样机的刚度过大、灵敏度欠佳且加载盘质量占比高。考虑到支路传感器结构复杂,结合溅射工艺、加工工艺和生产成本,选取上、下加载盘作为传感器轻量化设计的主体。
4 Stewart式六维力传感器加载盘轻量化设计
4.1 加载盘尺寸参数优化
Stewart式六维力传感器初始样机中上、下加载盘的主要尺寸参数如图5和图6所示。

图5 上加载盘半剖视图Fig.5 Half-section diagram of upper loading plate

图6 下加载盘半剖视图Fig.6 Half-section diagram of lower loading plate
由图5和图6可知,上加载盘的可优化参数为通孔直径φ1(初始值为182 mm)及沉台深度H1(初始值为2.5 mm),下加载盘的可优化参数为通孔直径φ2(初始值为202 mm)及沉台深度H2(初始值为2.5 mm)。因此,下文主要分析加载盘尺寸参数φ1、φ2、H1和H2对 Stewart式六维力传感器强度、刚度及质量的影响。
由于机械接口、制造工艺等因素的影响,尺寸参数φ1的可优化范围为182~188 mm,φ2的可优化范围为202~212 mm,H1的可优化范围为2.5~8.0 mm,H2的可优化范围为2.5~5.0 mm。经分析计算可知,φ1、φ2对Stewart式六维力传感器质量的影响不到2.2%,对刚度的影响不到1.5%,而H1、H2对质量的影响达13%~15%。因此,设定φ1=188 mm,φ2=212 mm,分析H1、H2对 Stewart式六维力传感器强度、刚度和质量的影响规律。为便于分析,定义K1和K2分别为:
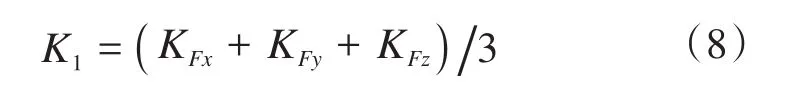
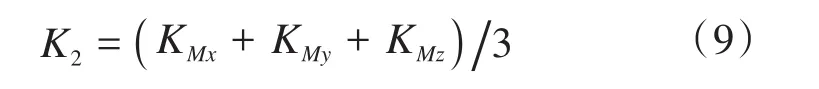
式中:KFx、KFy、KFz分别为沿x、y、z方向的拉压刚度;KMx、KMy、KMz分别为沿x、y、z方向的扭转刚度。
根据H1、H2的可优化范围,利用ABAQUS软件对Stewart式六维力传感器在不同H1、H2下的强度(满量程、全荷载作用下的最大应力)、刚度(拉压刚度K1和扭转刚度K2)和质量进行数值仿真分析,结果如图7至图10所示。
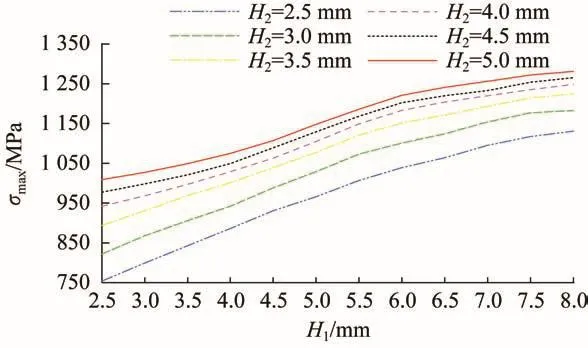
图7 H1、H2对Stewart式六维力传感器最大应力的影响Fig.7 Effect of H1,H2on maximum stress of Stewart type six-axis force sensor
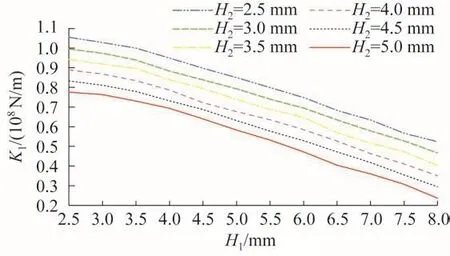
图8 H1、H2对Stewart式六维力传感器拉压刚度的影响Fig.8 Effect of H1,H2on tension stiffness of Stewart type six-axis force sensor
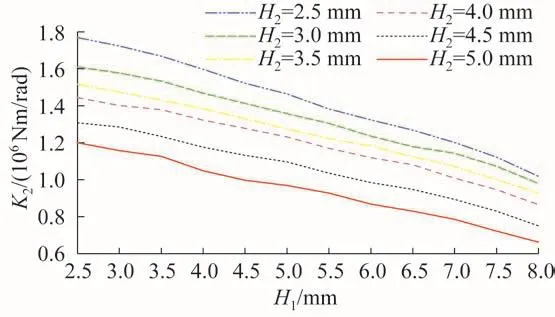
图9 H1、H2对Stewart式六维力传感器扭转刚度的影响Fig.9 Effect of H1,H2on torsional stiffness of Stewart type six-axis force sensor
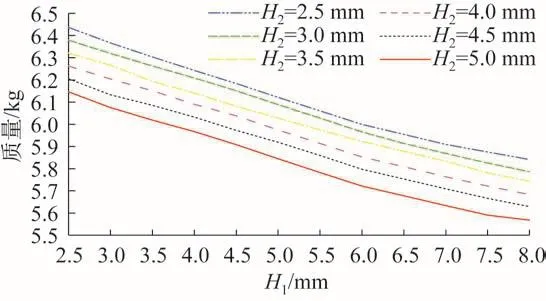
图10 H1、H2对Stewart式六维力传感器质量的影响Fig.10 Effect of H1,H2on mass of Stewart type sixaxis force sensor
由图7至图10可知,随着H1、H2的增大,Stewart式六维力传感器的最大应力不断增大,而其刚度和质量不断减小。根据其设计要求,H1、H2可分别优化为4.5 mm和4.0 mm。优化后Stewart式六维力传感器的最大应力为987.6 MPa,拉压刚度KFx=0.672 5×108N/m,KFy=0.653 1×108N/m,KFz=1.057 7×108N/m,扭转刚度KMx=1.167 5×106Nm/rad,KMy=1.003 1×106Nm/rad,KMz=1.756 8×106Nm/rad,质量为5.991 kg。
4.2 加载盘减重结构优化设计
Stewart式六维力传感器上、下加载盘的原减重结构如图11所示。
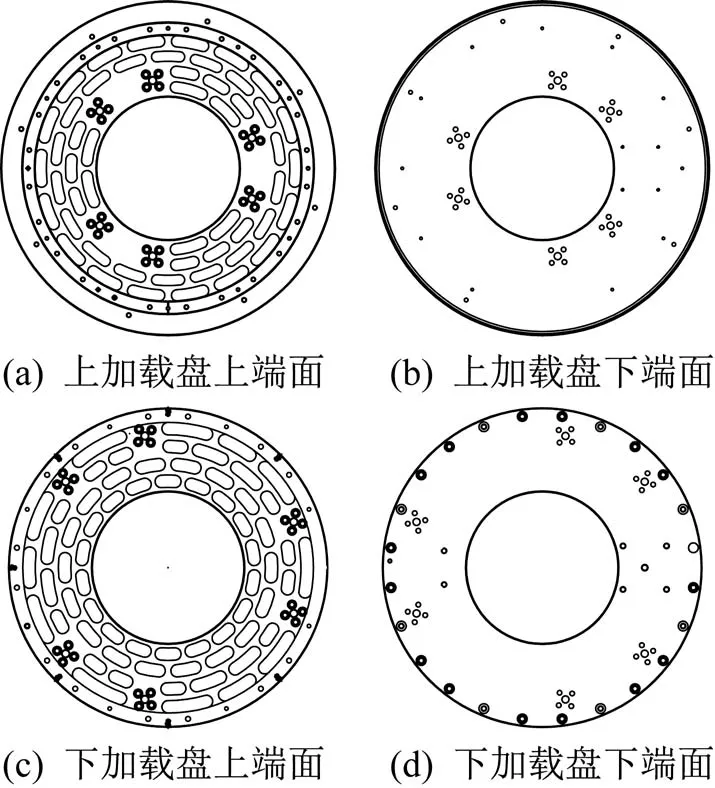
图11 原加载盘减重结构示意Fig.11 Schematic diagram of original weight reduction structure of loading plate
由图11可知,Stewart式六维力传感器加载盘减重结构为分布于加载盘上端面的单层矩形槽,该结构可加工性较好且抗拉压能力强,但抗扭转性较差、质量分布均匀性欠佳及质量利用率低。为改善上述问题,须对加载盘减重结构进行优化设计。鉴于球形结构具有良好的抗拉压/抗扭转能力且抗各向变形的同性度高,以及正四面体具有良好的结构稳定性,设计了一种具有一定对称性的“半球形”减重结构,如图12所示,即以半球形区域(半径为R)作为材料移除部位,4个半球形区域位于正四面体的4个顶点处,共同构成一个半球形减重单元,正四面体的高度等于优化区域厚度。半球形减重结构除具有球形结构和正四面体的优点外,还可改善加载盘的质量分布状态,提高了其质量分布的均匀性。
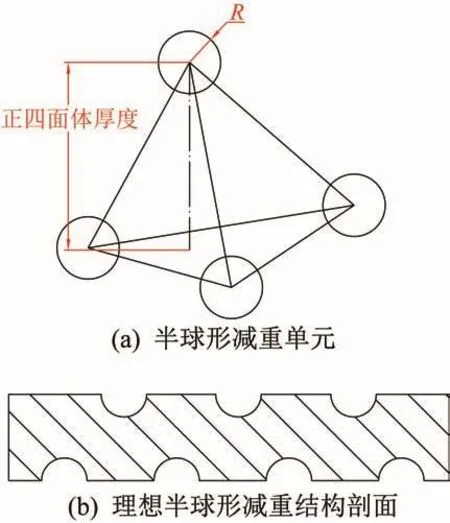
图12 半球形减重结构示意Fig.12 Schematic diagram of hemispherical weight reduction structure
由加载盘结构可知,上、下加载盘可优化区域为圆环形区域,考虑到工艺需求及加工的可行性,上加载盘可优化区域为直径等于182~308 mm的圆环状区域,下加载盘可优化区域为直径等于202~364 mm的圆环状区域。结合加工效率,针对上、下加载盘各提出2种优化方案。为方便分析,在加载盘端面环形区域标记等间距圆(定义为位置圆),如图13所示。半球形区域的球心均布于位置圆上,同时为保证半球形减重单元的正四面体特性,加载盘上、下端面位置圆的数量相差1。将位置圆1(基准)定义在位置圆个数为奇数的加载盘端面上,其半径等于环形优化区域最小半径与最大半径之和的一半;相邻位置圆之间半径差等于正四面体边长。同理,可确定位置圆个数为偶数的加载盘端面上的减重结构。
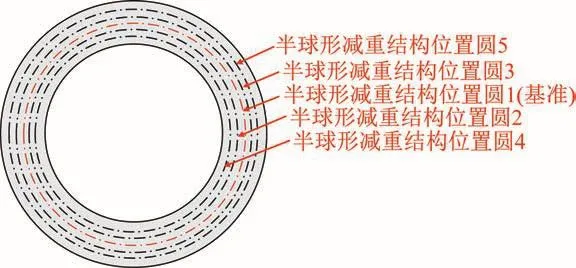
图13 半球形减重结构位置圆定义Fig.13 Definition of position circle of hemispherical weight reduction structure
1)上加载盘优化方案1。
上加载盘的优化方案1为:上加载盘上端面设置3列等间距半球形减重单元,下端面设置4列等间距半球形减重单元,如图14所示。
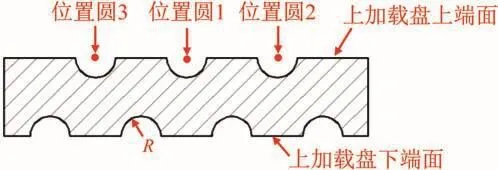
图14 上加载盘优化方案1Fig.14 Optimization scheme 1 of upper loading plate
2)上加载盘优化方案2。
上加载盘的优化方案2为:上加载盘上端面设置4列等间距半球形减重单元,下端面设置5列等间距半球形减重单元,如图15所示。
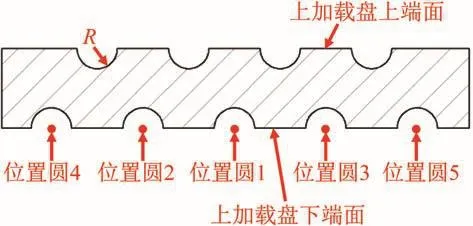
图15 上加载盘优化方案2Fig.15 Optimization scheme 2 of upper loading plate
3)下加载盘优化方案1。
下加载盘的优化方案1为:下加载盘上端面设置4列等间距半球形减重单元,下端面设置5列等间距半球形减重单元,如图16所示。
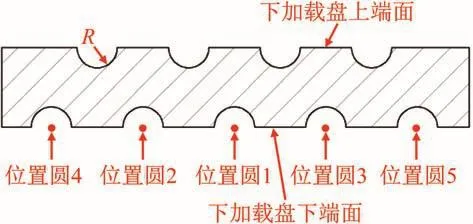
图16 下加载盘优化方案1Fig.16 Optimization scheme 1 of lower loading plate
4)下加载盘优化方案2。
下加载盘的优化方案2为:下加载盘上端面设置5列等间距半球形减重单元,下端面设置6列等间距半球形减重单元,如图17所示。
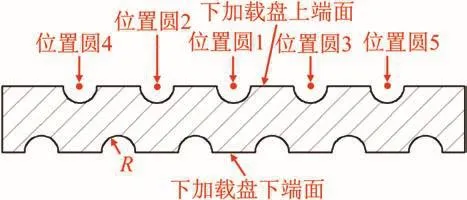
图17 下加载盘优化方案2Fig.17 Optimization scheme 2 of lower loading plate
取半球形区域半径为设计变量,参照4个优化方案,依据设计要求建立Stewart式六维力传感器加载盘结构参数的优化数学模型:

式中:V为加载盘体积。
根据上、下加载盘的优化方案,利用ABAQUS软件对加载盘减重结构不同的Stewart式六维力传感器进行仿真分析,具体过程如图18所示。
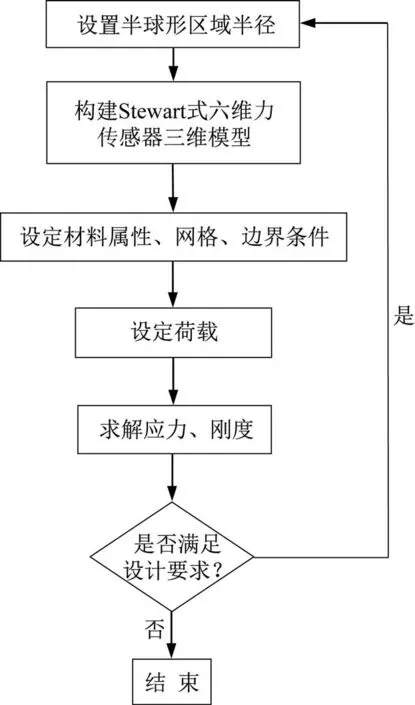
图18 加载盘减重结构优化设计过程Fig.18 Optimization design process of loading plate weight reduction structure
设半球形区域半径的初始值为10 mm,以0.1 mm为间隔依次递减;加载盘材料为7A04,网格单元为C3D10M,网格单元尺寸为4 mm;螺钉、销钉处施加固定约束,利用MPC模块中的梁约束进行外荷载施加等效设置,荷载值参见表2,仿真至最大应力、刚度不满足设计要求时结束。经反复验证,最终确定上加载盘采取优化方案1,下加载盘采取优化方案2,即上加载盘半球形区域半径取8.2 mm,下加载盘半球形区域半径取7.8 mm。优化后上、下加载盘的端面结构如图19所示。
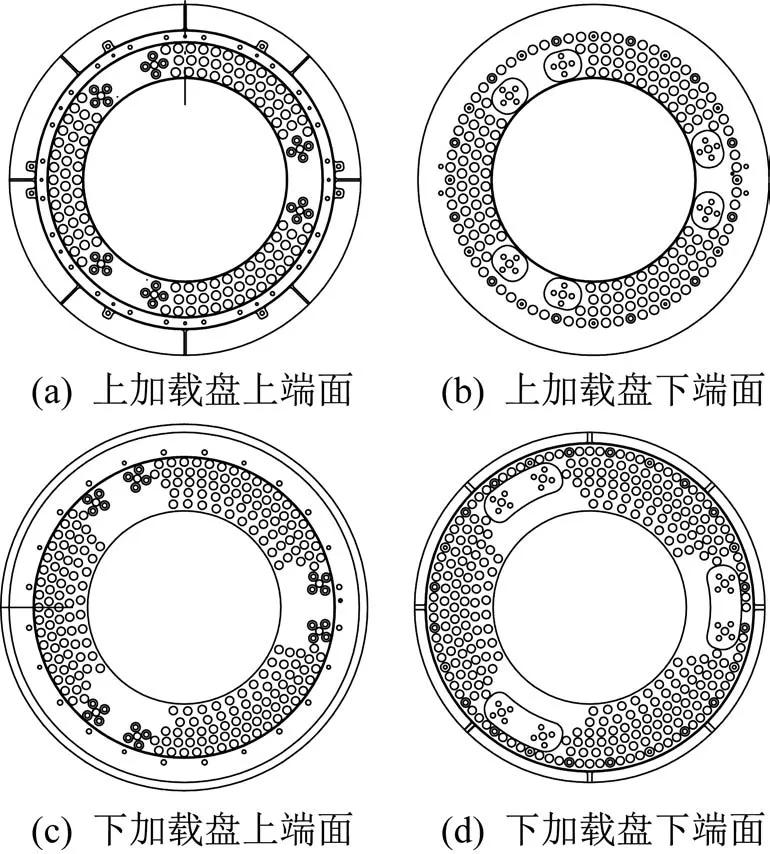
图19 优化后的加载盘端面结构示意Fig.19 Schematic diagram of end face structure of loading plate after optimization
优化后Stewart式六维力传感器的质量为5.216 kg,相较于优化前下降了18.97%。通过仿真可得其主要性能如表6所示。
由表 6 可知,在单向力/力矩(Fx、Fy、Fz、Mx、My、Mz)作用下,相较于优化前,优化后Stewart式六维力传感器,最大应力依次变化了11.98%,10.89%,10.43%,14.96%,-5.17%和8.64%,平均应力依次变化了8.46%,12.13%,8.91%,13.19%,-3.31%和8.12%,刚度依次变化了-7.42%,-5.84%,-16.57%,-12.07%,-7.16%和-10.53%,灵敏度依次变化了12.50%,16.00%,15.71%,20.34%,-2.79%和12.51%。
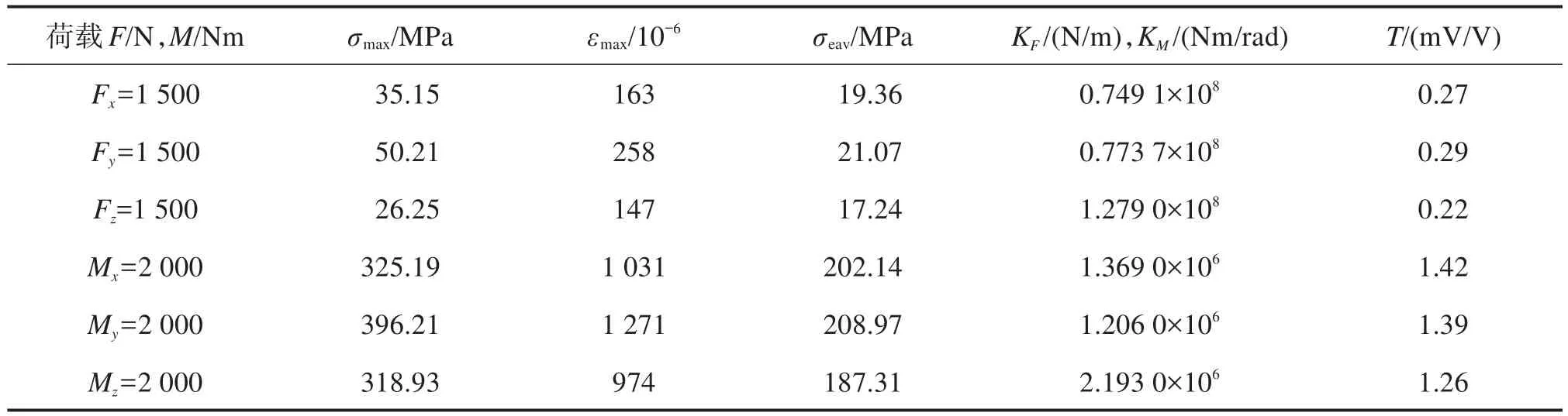
表6 优化后Stewart式六维力传感器的性能Table 6 Performance of Stewart type six-axis force sensor after optimization
图20所示为优化后Stewart式六维力传感器在满量程、全荷载作用下的应力云图。由图可知,优化后其最大应力为930.4 MPa,满足设计要求(小于1 000 MPa)。

图20 优化后Stewart式六维力传感器的应力云图Fig.20 Stress cloud diagram of Stewart type six-axis force sensor after optimization
5 Stewart式六维力传感器优化样机性能实验与分析
参照优化结果,制作Stewart式六维力传感器优化样机,如图21所示。

图21 Stewart式六维力传感器优化样机Fig.21 Optimized prototype of Stewart type six-axis force sensor
5.1 质量分析
对Stewart式六维力传感器优化样机进行整机质量测定,可得优化后的整机质量为5.738 kg,相较于初始样机(整机质量为6.967 kg,含约0.530 kg的外部放大组件)下降了17.65%,满足设计要求(小于6.000 kg)。
5.2 静态标定及测量误差分析
假设Stewart式六维力传感器为线性系统,则其静态标定实质上是利用施加的广义力F和通过采集卡采集的6个输出信号所构成的向量组U求得标定矩阵C[14-15],C=F(UTU)-1UT。
为此,研制了专用的Stewart式六维力传感器标定装置(满足宇航产品技术指标实验要求),如图22所示,其主要由校准中心台、S型力传感器、滑轮、螺纹加力组件及加载盘构成。

图22 Stewart式六维力传感器标定装置Fig.22 Calibration device of Stewart type six-axis force sensor
在特制的标定装置上对Stewart式六维力传感器优化样机进行标定,具体步骤如下[16]:
1)参照校准中心台上的位置标记,使用力矩扳手将传感器优化样机安装至校准中心台上。
2)传感器优化样机按规定激励电源供电(±12 V)并预热30 min,显示仪表等预热15 min以上。
3)在传感器优化样机量程范围内选6个测量点(包含零点和满量程点)。
4)针对6个方向(沿x、y、z轴向和绕x、y、z轴旋转方向),完成传感器优化样机的加载与记录,每个方向上需完成3次有效加载与记录。加载方式为:将荷载按测量点从零逐渐加载至满量程,然后减小至零,再逐渐增加至负方向满量程,然后减小至零,完成一个测试循环。到达各加载点时保持5~10 s后记录相应的输出值(每个方向正式标定前须按上述方法预加载3次)。
5)采用最小二乘法求解得到3组标定矩阵并进行平均化处理,最终得到平均标定矩阵。
6)参照不同使用工况进行耦合补偿,得到各工况下的(标准)标定矩阵。
式(11)为求解得到的常温常压状态下优化后Stewart式六维力传感器样机的标定矩阵C:

通常以Stewart式六维力传感器的标定误差矩阵作为其单维精度和维间耦合的度量。单维精度由Ⅰ类误差表示,即测量力/力矩与实际施加力/力矩的差值,其为标定误差矩阵中的对角线元素;维间耦合由Ⅱ类误差表示,由非对角线元素表示不同维间耦合程度。标定误差矩阵δ[17-18]可表示为:
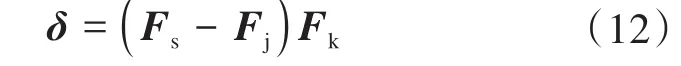
式中:Fs为施加于Stewart式六维力传感器的6×6维标定力/力矩矩阵;Fj为基于标定数据理论计算得到的6×6维力/力矩矩阵;Fk为由各维满量程力/力矩构成的6×6维对角矩阵。
结合式(2)、式(11)和式(12),求得Stewart式六维力传感器优化样机的标定误差矩阵δu:
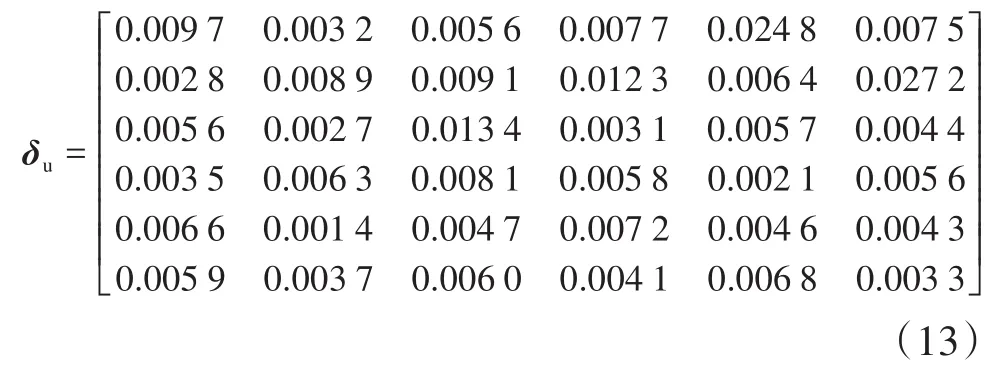
由式(13)可知,对于Stewart式六维力传感器优化样机,其x、y、z方向的力测量精度分别为0.97%,0.89%和1.34%,其x、y、z方向的力矩测量精度分别为0.58%,0.46%和0.33%,最大I类误差为1.34%,出现在z方向上。其中:当加载My时,x方向上产生的维间耦合误差为2.48%;当加载Mz时,y方向上产生了2.72%的维间耦合误差,维间耦合较明显。综上可知,Stewart式六维力传感器优化样机的测量精度为2.72%,满足设计要求。
5.3 刚度及灵敏度分析
按照国家军用测试标准,对Stewart式六维力传感器优化样机进行刚度及灵敏度测试,结果如表7所示。由表7可知,相较于初始样机,Stewart式六维力传感器优化样机在单向力/力矩(Fx、Fy、Fz、Mx、My、Mz)的作用下,其刚度依次变化了-7.34%,-5.61%,-16.15%,-12.13%,-6.31%和-10.61%,灵敏度依次变化了8.00%,11.54%,17.65%,19.85%,-3.51%和7.76%,这与仿真结果基本吻合。
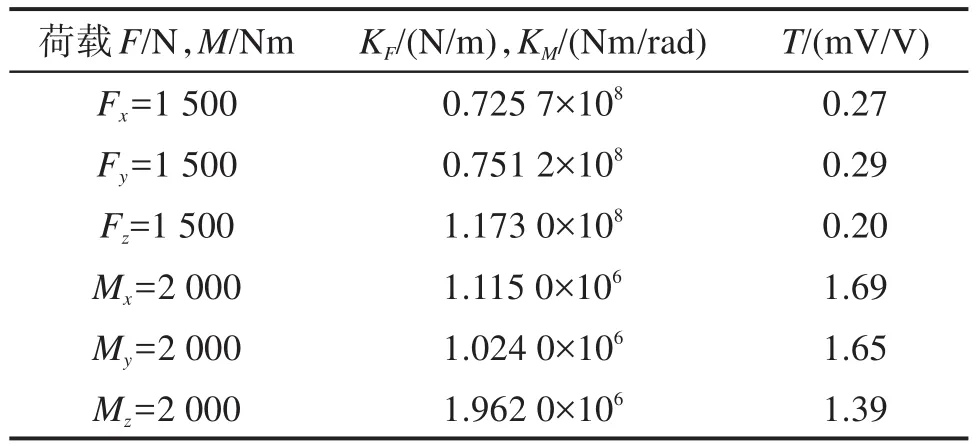
表7 Stewart式六维力传感器优化样机的刚度、灵敏度Table 7 Stiffness and sensitivity of optimized prototype of Stewart type six-axis force sensor
5.4 工作带宽分析
对Stewart式六维力传感器优化样机进行整机工作带宽测试。通过测量得到,优化后整机的工作带宽约为1 kHz,与优化前的基本相同,符合设计要求。由此可见,轻量化设计并未对Stewart式六维力传感器整机的工作带宽产生明显影响。
6 结论
本文对Stewart式六维力传感器进行了轻量化设计,所得结果如下。
1)基于螺旋理论,建立了Stewart式六维力传感器的力映射模型,并结合多目标综合性能优化函数,有效解决了该传感器多项力学性能难以综合优化的问题,极大地减少了仿真分析的运算量,并能获取特定约束条件下传感器的最优结构参数。
2)设计了一种具有正四面体特征的半球形减重结构,其具备良好的抗拉压/抗扭转能力且抗各向变形同性度高、结构稳定性好及可加工性强,可有效改善Stewart式六维力传感器上、下加载盘质量分布不均以及质量利用率低的问题。
3)经理论推导、数值仿真及实验验证结果可知,优化后Stewart式六维力传感器的整机质量下降了17.65%,灵敏度提升了7.76%~19.85%,且测量精度、刚度、强度及工作带宽均符合设计要求。
研究结果可为Stewart式六维力传感器性能的综合优化提供一定的参考。
