变排量非对称轴向柱塞泵抗扰控制及并行整定方法

宁志强，卫立新，权 龙，赵美卿，高有山

（1.太原科技大学机械工程学院，山西 太原 030024；2.山西工程技术学院机械电子工程系，山西 阳泉 045000；3.太原理工大学机械与运载工程学院 山西 太原 030024）

电液控制系统可分为阀控和泵控（无阀）两类。其中，阀控系统节流会造成较大的功率损失，减少或消除节流损失可以显著降低电液控制系统的能量消耗［1］。与阀控系统相比，泵控系统在节能方面具有较大优势。目前，泵控对称缸技术比较成熟，但对于泵控差动缸技术而言，因差动缸的两腔（有杆腔和无杆腔）结构不对称，其应用受到了一定的限制。为解决泵控差动缸系统因结构不对称而导致流量不相等的问题，太原理工大学的Zhang等［2-3］、Huang等［4］提出了并联型三配流窗口轴向柱塞泵，并利用该泵控制单出杆差动缸，同时对其进行了系统的仿真分析和试验研究；太原科技大学的高有山等［5］对变排量非对称轴向柱塞泵的特性进行了研究，通过控制斜盘角度来改变该泵的排量。但变排量非对称轴向柱塞泵在运行过程中存在瞬时流量脉动，导致油液压力变化较大，因此有必要进一步解决该泵的压力冲击、流量脉动和斜盘变量阻力矩较大的问题。太原理工大学的杨伽迪等［6］提出，通过在变排量非对称轴向柱塞泵中增加阻尼孔来减少斜盘振荡，以提高其控制性能，但阻尼孔的增加会加剧油液泄漏，造成功率损失。

目前，液压伺服控制系统常采用常规PID（proportion integration differentiation，比例积分微分）控制算法，但其抗扰能力较差，因此须采用其他抗扰控制算法来提高系统的控制性能。例如：王慧等［7］研究了阀控变量泵系统的动态特性及抗扰特性；吴斌等［8］设计了泵阀并联驱动液压缸的抗扰控制器。抗扰控制算法为解决变排量非对称轴向柱塞泵的斜盘振荡问题提供了一种新思路，即可将变量阻力矩视作干扰信号，通过补偿变量阻力矩来减小斜盘振荡。常见的抗扰控制算法有指数收敛干扰观测器控制、自抗扰控制、非线性PID控制和滑模控制等，但各抗扰控制算法对不同频率干扰信号的补偿效果不同。因此，有必要研究不同抗扰控制算法对变排量非对称轴向柱塞泵斜盘振荡的抑制性能，以得到最合适的抗扰控制算法。

针对以上问题，笔者通过仿真对比了常规PID控制、指数收敛干扰观测器控制、非线性PID控制、自抗扰控制和滑模控制的抗扰性能，以得到适用于改善变排量非对称轴向柱塞泵斜盘振荡的抗扰控制算法。同时，在此基础上，提出基于粒子群优化（particle swarm optimization，PSO）的并行整定方法，以对主要控制参数进行快速、并行整定，并利用SimulationX平台进行二次开发，以实现抗扰控制算法的性能优化，即减小最大超调量和跟踪误差。

1 变排量非对称轴向柱塞泵的控制原理

变排量非对称轴向柱塞泵的主要结构如图1所示［9］，其具有3个油口（A口、B口和T口）。当该泵用于势能回收系统时，其A口与差动缸的无杆腔相连，B口与差动缸的有杆腔相连，T口与蓄能器相连。

图1 变排量非对称轴向柱塞泵的结构示意Fig.1 Structure diagram of variable displacement asymmetric axial piston pump

变排量非对称轴向柱塞泵是通过变排量机构控制斜盘角度来实现排量变化的，其控制原理如图2所示。其中：变排量机构主要包括变量缸、比例伺服阀和dSPACE控制器等［9］。将角位移传感器固定在斜盘上，实时采集斜盘角度并计算其与给定目标角度的偏差，通过dSPACE控制器的输出信号来驱动比例伺服阀，从而达到控制斜盘角度的目的。

图2 变排量非对称轴向柱塞泵的控制原理Fig.2 Control principle of variable displacement asymmetric axial piston pump

变排量非对称轴向柱塞泵中斜盘所承受的力矩的来源较为复杂，主要包括变量缸对斜盘的转矩，滑靴组件对斜盘的力矩，斜盘的惯性力矩以及滑靴与球铰之间、斜盘与支撑轴承之间的摩擦力矩。推导得到斜盘的运动方程，可表示为：

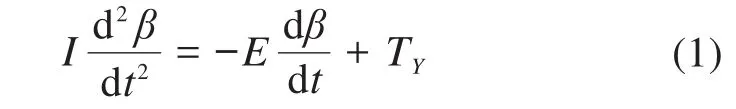
式中：I为斜盘相对于自身转轴的转动惯量；β为斜盘角度；E为斜盘的黏性阻尼系数；TY为滑靴组件对斜盘转轴的合力矩（斜盘绕Y方向转动），即变量阻力矩。

由此可得，斜盘的变量阻力矩TY为：

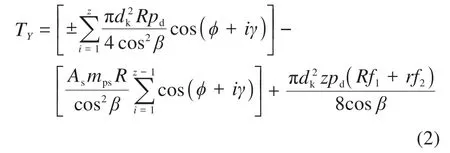
式中：dk为柱塞直径；R为柱塞的分布圆半径；pd为供油压力；z为柱塞个数；φ+iγ为第i个柱塞的转角，其中φ为某特定柱塞的转角，γ为柱塞孔之间的夹角；As为滑靴副相对于缸体的角加速度；mps为柱塞和滑靴的质量；r为滑靴副球头半径；f1为斜盘与滑靴间的滑动摩擦系数；f2为斜球铰的滑动摩擦系数，润滑充分条件下取f2=0.08。

将比例伺服阀的输入电压u1和斜盘的变量阻力矩TY视作干扰信号，则变排量非对称轴向柱塞泵控制系统的闭环控制框图如图3所示［10-11］。

根据图3，构建变排量非对称轴向柱塞泵控制系统的开环传递函数G（s）以及其干扰信号的传递函数D（s），可分别表示为：

图3 变排量非对称轴向柱塞泵控制系统的闭环控制框图Fig.3 Closed-loop control block diagram of control system of variable displacement asymmetric axial piston pump

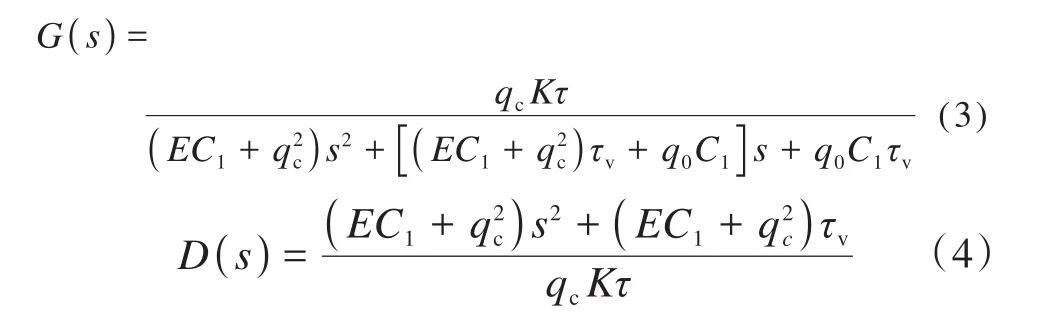
式中：q0为与变量缸弹簧刚度和力臂有关的参数；qc为与作用力臂有关的参数；C1为变量缸总泄漏系数；τ和τv为与比例伺服阀时间常数有关的参数；K为比例伺服阀的流量增益。

2 常规PID控制下变排量非对称轴向柱塞泵的控制试验

在常规PID控制下变排量非对称轴向柱塞泵的控制试验中，通过dSPACE控制器控制比例伺服阀来驱动变量缸，以改变斜盘角度，从而实现变排量的目的。试验用变排量非对称轴向柱塞泵如图4所示［5］，控制试验主要设备的参数如表1所示。其中：角位移传感器用于获取实时的斜盘角度；比例伺服阀用于控制油液流量的大小和方向；流量压力传感器用于测量B口和T口的流量和压力。

图4 变排量非对称轴向柱塞泵实物Fig.4 Physical object of variable displacement asymmetric axial piston pump

表1 变排量非对称轴向柱塞泵控制试验主要设备的型号和参数Table 1 Models and parameters of main equipment for control test of variable displacement asymmetric axial piston pump

在控制试验中，PID的控制参数设置如下：比例系数P=2，积分时间常数I=0.9，微分时间常数D=0.01。令电机的转速为1 000 r/min，设定斜盘的目标角度为±5°。当电动机启动后，在0—20 s阶段，斜盘的目标角度保持为0°；在20—46 s阶段，斜盘的目标角度为5°；46 s后将斜盘的目标角度调整为-5°；62 s后再次调整斜盘的目标角度，调整为5°；86 s后又一次调整斜盘的目标角度，调整为-5°。图5所示为常规PID控制下斜盘的目标角度和响应角度。

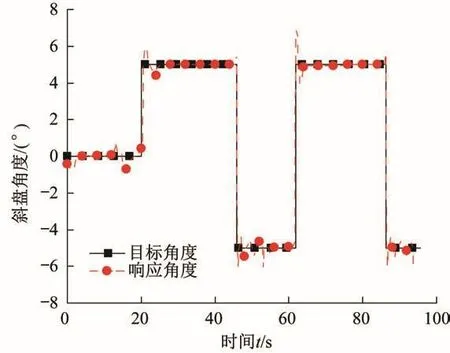
图5 常规PID控制下斜盘的目标角度和响应角度对比Fig.5 Comparison of target angle and response angle of swash plate under conventional PID control

由图5可知，变排量非对称轴向柱塞泵斜盘的响应角度与目标角度存在较大差异，说明斜盘存在振荡，这是由较大的变量阻力矩TY引起的。由式（2）可知，变量阻力矩TY的幅值和频率较难确定，故不易对干扰直接进行补偿。虽然常规PID控制系统具有原理简单和实用面广等优点，但其性能在有干扰信号时较差。因此，应采用抗扰控制算法来解决斜盘振荡问题。

3 变排量非对称轴向柱塞泵的抗扰控制

3.1 常用的抗扰控制算法

3.1.1 指数收敛干扰观测器

干扰观测器是基于估计输出与实际输出的差值来对估计值进行补偿的。指数收敛干扰观测器可设计为［12］：

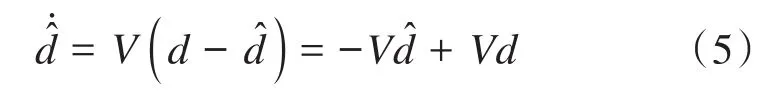
3.1.2 非线性PID控制器

常用的非线性PID控制器ῶ设计为：

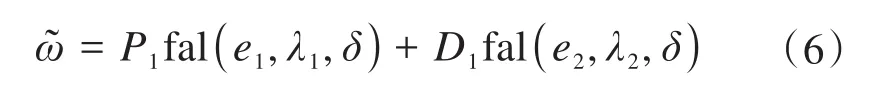
式中：P1、D1分别为比例系数和微分时间常数；λ1、λ2为设计参数；e1为被控对象期望位置与输出位置之差；e2为被控对象期望位置的微分与输出位置的微分之差；δ为线性段的区间长度；fal（）为幂函数。

为避免高频振荡现象，将幂函数设计为饱和函数，可表示为：

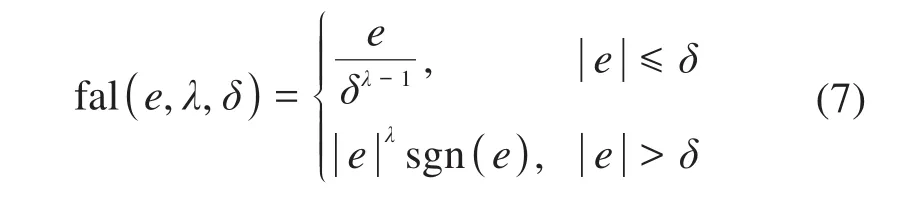
3.1.3 自抗扰控制器

自抗扰控制的非线性微分跟踪器设计为［13-15］：

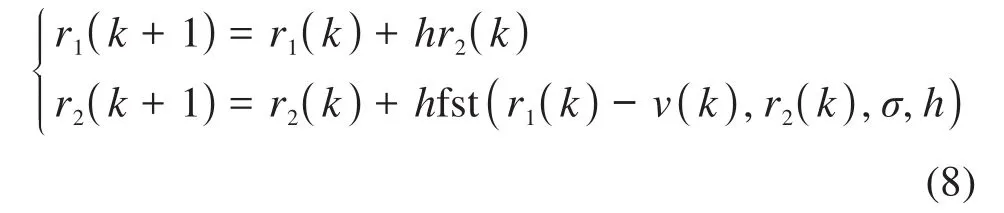
式中：r1（k）、r2（k）分别为k时刻输入信号v（k）及其微分v̇（k）的跟踪信号；h为采样周期；σ为决定跟踪速度的参数；fst()为最速控制综合函数。

在自抗扰控制中，利用微分跟踪器实现过渡，利用线性扩张观测器实现扰动估计和补偿。线性扩张观测器设计为：

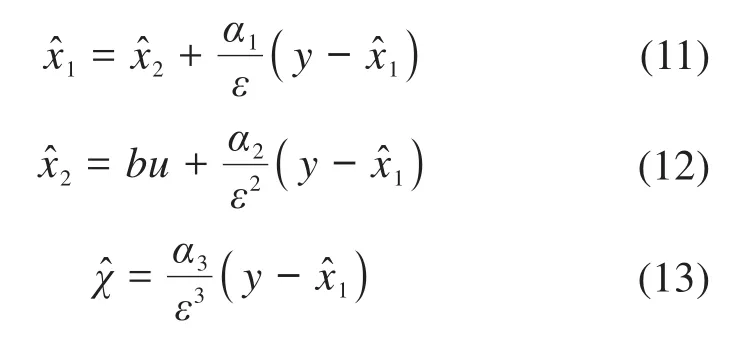
自抗扰控制器也采用非线性PID控制，非线性PID控制器设计参见3.1.2节。

3.1.4 滑模控制器

为减少滑模抖动，采用准滑动模态滑模控制算法。与理想滑模控制不同的是，准滑动模态滑模控制可使一定范围内的状态点均被吸引至某一邻域内，从根本上避免或削弱了抖振，其在实际中得到了广泛应用［12］。

在准滑动模态滑模控制器中，用连续函数θ（ψ）取代常规滑模控制算法中的sgn（ψ）：

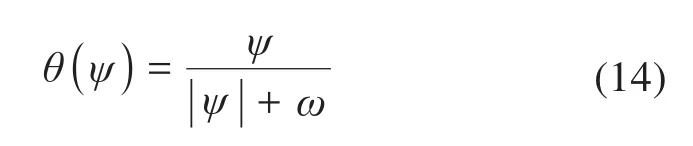
式中：ω为滑模切换面边界层参数，其为很小的正常数；ψ为滑模函数。

准滑动模态滑模控制器设计为：

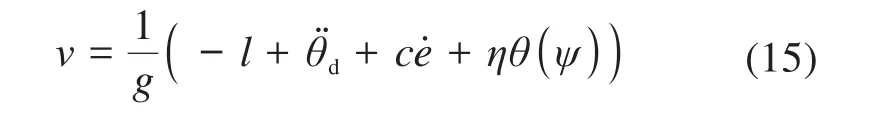
式中：v为滑模控制器输出；θd为目标角度；e为误差，e=θd-θ；c为滑模切换面参数；ψ=ė+ce；η为切换项增益；g、l为与控制对象传递函数相关的参数。

3.2 抗扰控制仿真

SimulationX平台是一款适用于多学科领域建模、仿真和分析的通用CAE（computer aided engineering，计算机辅助工程）工具，其元件库包括1D力学、3D多体系统、动力传动系统和液力学等。采用SimulationX平台建立变排量非对称轴向柱塞泵控制系统的仿真模型如图6所示。

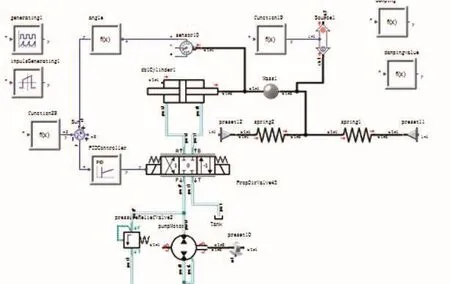
图6 变排量非对称轴向柱塞泵控制系统的仿真模型Fig.6 Control system simulation model of variable displacement asymmetric axial piston pump

Simulink平台具备与SimulationX平台联合仿真的功能，故本文采用Simulink平台搭建抗扰控制器。构建的自抗扰控制器和非线性PID控制器如图7所示。

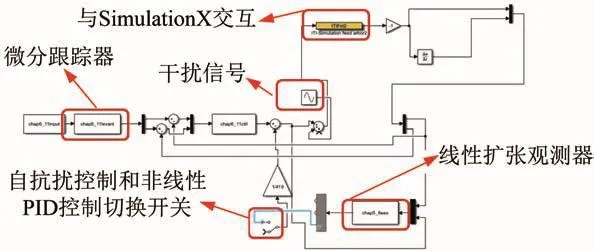
图7 自抗扰控制器和非线性PID控制器Fig.7 Active anti-interference controller and nonlinear PID controller

取干扰信号为正弦信号，其频率依次取10，20和100 Hz，幅值均为0.05。联合利用SimulationX平台构建的变排量非对称轴向柱塞泵控制系统的仿真模型和利用Simulink平台构建的抗扰控制器，通过仿真得到不同干扰信号作用下斜盘角度（目标角度为8°）的响应特性，结果如图8所示。对应条件下斜盘角度的波动量如表2所示。

从图8和表2可以看出：相比于常规PID控制，非线性PID控制具有较强的抗扰性能。随着干扰信号频率的增大，指数收敛干扰观测器控制的抗扰性能下降，说明该方法仅适用于对低频干扰信号的补偿，鉴于其在100 Hz干扰信号下的抗扰性能较差，结果不计入统计。在10 Hz和20 Hz干扰信号下，自抗扰控制的抗扰性能良好，但比滑模控制稍差，且其对高频干扰信号的抑制效果也不理想，此时斜盘角度的波动量较大。相比于其他抗扰控制算法，滑模控制的抗扰效果明显；在10，20和100 Hz干扰信号的作用下，常规PID控制下斜盘角度的波动量分别为1.700°，1.300°和0.080°，而滑模控制下分别为0.030°，0.029°和0.019°，仅为常规PID控制下的1.7%，2.2%和23.0%。

图8 不同干扰信号作用下采用不同抗扰控制算法时的斜盘角度响应曲线对比Fig.8 Comparison of swash plate angle response curves with using different anti-interference control algorithms under the action of different interference signals

表2 不同干扰信号作用下采用不同抗扰控制算法时的斜盘角度波动量对比Table 2 Comparison of swash plate angle fluctuation with using different anti-interference control algorithms under the action of different interference signals

斜盘振荡会直接影响变排量非对称轴向柱塞泵输出流量的稳定性。提取采用滑模控制、常规PID控制和自抗扰控制时B口流量的仿真结果并进行对比分析，结果如图9所示（20 Hz干扰信号作用下）。由图9可知，从整体上来看，B口流量的波动趋势与斜盘角度的波动趋势基本一致；滑模控制下B口流量输出平稳，其次是自抗扰控制下，常规PID控制下波动最大。

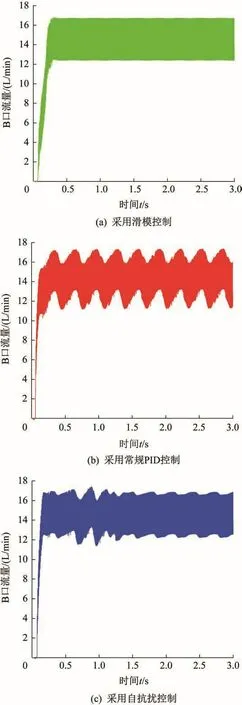
图9 20 Hz干扰信号作用下采用不同抗扰控制算法时的B口流量对比Fig.9 Comparison of B-port flow with using different antiinterference control algorithms under the action of 20 Hz interference signal

为分析滑模控制的性能，在不施加任何干扰的条件下，对滑模控制下斜盘角度的响应特性进行分析，结果如图10所示。从图10中可以看出，虽然没有施加干扰，但由于所采用仿真平台自带的物理对象建模法充分考虑了时间上的延迟和空间上的滞后，使得滑动模态呈抖动形式，即在光滑的滑动面上叠加了抖振，而抖振问题是影响滑模控制广泛应用的主要障碍。合理地设置滑模控制参数有助于改善其控制性能，因此有必要对滑模控制参数进行整定。

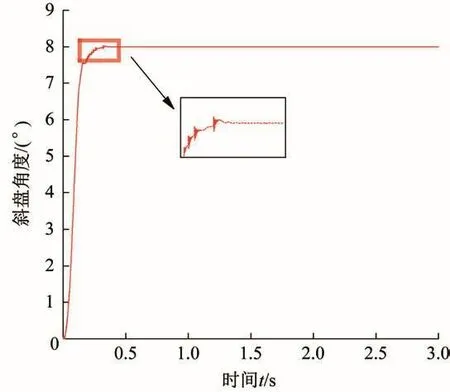
图10 滑模控制下斜盘角度的响应特性（无干扰）Fig.10 Response characteristics of swash plate angle under sliding mode control(without interference)

4 基于PSO的滑模控制参数并行整定方法

针对液压系统仿真时耗时较长和效率较低，且受仿真平台限制的问题，提出一种脱离仿真平台的基于PSO的控制参数并行整定方法。该方法将SimulationX仿真模型转换为后缀为exe的仿真程序，其能够独立运行于任何Windows操作系统，解决了依赖于仿真平台的问题。此外，exe仿真程序由C代码生成，其运行效率较高。每个exe仿真程序分配一组设计变量，同时开启多个程序即可实现并行整定［16］。同时，采用PSO协调分配每个exe仿真程序的参数，以实现特定目标函数最优化［17-19］。基于PSO的控制参数并行整定方法的整体框架如图11所示。

图11 基于PSO的控制参数并行整定方法的整体框架Fig.11 Overall framework of parallel tuning method of control parameters based on PSO

基于PSO的控制参数并行整定方法的伪代码程序如下：

1开始；

2初始化PSO参数：并行仿真的程序数量Npop，仿真最大迭代次数MAXITER，计数器t=0；

3随机初始化仿真参数；

4并行运行Npop个exe仿真程序，计算目标函数（跟踪误差）；

5完成初始化；

6 While（不满足结束条件）

7 Do

8 PSO根据目标函数数值（跟踪误差）更新仿真参数，输出到Npop个参数文件中；

9并行运行Npop个exe仿真程序，计算目标函数；

10 t=t+1；

11输出最优仿真参数和最优目标函数值；

12结束；

在本文中，优化目标为滑模控制下变排量非对称轴向柱塞泵斜盘角度的跟踪误差μ=∫||e dt，其中|e|为绝对值误差；设计变量为滑模切换面参数c，切换项增益η，滑模切换面边界层参数ω。取斜盘的目标角度为8°，施加频率为100 Hz、幅值为0.05的正弦干扰信号。采用C++语言编写基于PSO的滑模控制参数并行整定程序，以实现人机交互界面的可视化和参数化，并显示斜盘角度响应曲线。所设计的滑模控制参数并行整定程序的人机交互界面如图12所示。

鉴于滑模控制参数并行整定程序采用PSO进行寻优，不同迭代次数对其整定效果和仿真耗时会有一定影响：迭代次数越多，寻优效果越好，但仿真耗时越长。因此，需要得到合理的迭代次数，既能获得良好的整定效果，又能使仿真耗时在可接受范围内。图13所示为迭代次数不同时滑模控制参数的整定效果。其中：图13（a）为迭代20次和50次时滑模控制的跟踪误差，图13（b）为滑模控制参数整定前后斜盘角度的响应对比。由图可知，随着迭代次数的增加，滑模控制的跟踪误差呈减小趋势，即斜盘角度的实际响应值与目标值的偏差变小，但迭代20次和50次时斜盘角度的偏差并不大，而迭代50次的耗时更长；滑模控制参数整定后，斜盘振荡明显小于整定前，且迭代50次的整定效果略优于迭代20次的。经50次迭代整定后，滑模切换面参数c=42.9，切换项增益η=100，滑模切换面边界层参数ω=0.012 3；整定后最大超调量明显减小，为0.021，相较于整定前的0.168减小了87.5%。

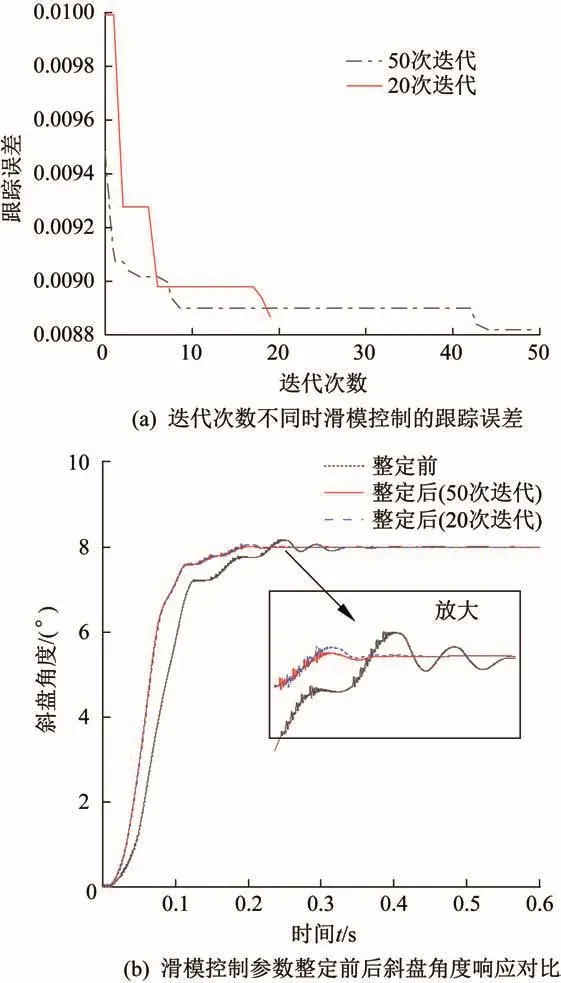
图13 基于PSO的滑模控制参数并行整定效果对比Fig.13 Comparison of parallel tuning effect of sliding mode control parameters based on PSO

利用SimulationX平台整定控制参数时需要反复手动调整仿真模型的参数，直到获得满意的结果。而手动调参方法依赖于经验，多个参数并行整定经常需调整几十次，甚至更多。经二次开发后的exe仿真程序采用Cvode外部求解器，该求解器的算法基于C代码编译，其对复杂模型的求解速度较快［20］。在对滑模控制参数进行整定时，单次SimulationX平台仿真耗时420 s，20次仿真则需耗时8 400 s；而并行整定程序进行20次迭代共耗时2 160 s左右，其同时运行200个exe仿真程序，每个exe仿真程序的平均耗时仅为10.8 s。由此可知，所设计的并行整定程序可利用多核计算机的多进程性能同时运行多个exe仿真程序，充分利用了多核CPU（central processing unit，中央处理器）的计算性能，与SimulationX平台相比，其计算效率提高了10倍以上。

5 结论

本文提出将变量阻力矩视作干扰信号并采用抗扰控制算法来提高变排量非对称轴向柱塞泵斜盘角度的响应性能。与常规PID控制、指数收敛干扰观测器控制、非线性PID控制和自抗扰控制相比，滑模控制能大幅减小斜盘振荡和流量脉动。在10，20和100 Hz干扰信号作用下，常规PID控制下斜盘角度的波动量分别为1.700°，1.300°和0.080°，而滑模控制下则为0.030°，0.029°和0.019°，仅为常规PID控制的1.7%，2.2%和23.0%。滑模控制参数经整定后，抖振得到抑制，跟踪误差和最大超调量均有效减小，整定后最大超调量为0.021，较整定前减小了87.5%。此外，提出的基于PSO的控制参数并行整定方法能够在任何Windows操作系统下独立运行，解决了液压动态仿真依赖于专业仿真软件的问题，且相比于专业仿真平台，其运行效率提高了10倍以上，该方法可为常规液压系统的并行仿真优化提供一定的借鉴。