基于机器视觉的轨道交通自动测距研究

毕嘉桢，沈 拓，2，张轩雄

(1.上海理工大学 光电信息与计算机工程学院，上海 200093； 2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室，上海 201804)

随着世界经济以及科学技术的高速发展，中国城市轨道交通规模也在逐年增加。随着轨道交通客流量的增大以及行车速度的提高，列车制动距离也随着惯性的增大而增大。由于制动距离不足而造成的列车追尾事故时有发生。城市轨道交通运行的安全性是保障居民平安出行的关键，行驶中前后列车之间的距离已成为列车运行安全的首要衡量标准，列车间距测量精度以及速度也尤为重要。

当列车行驶过程中出现信号灯故障或调度问题时，列车的高速度和远距离的特性导致通过人眼来准确估计与前方列车尾部的距离较为困难。为了保障列车在特殊情况下仍能安全行车，需要列车测距系统来测量与前方列车车尾的距离，并将其转化为可视化数据向驾驶员发出预警。

传统的测距手段有激光[1]、雷达[1-4]、超声波[5]等传感器技术。相对于传统的测距手段，视觉信号[6]的探测范围更广，目标信息更完整，成本也相对更低。文献[7]提出了一种基于融合雷达(用于距离测量)和图像传感器(用于障碍物检测)的铁路障碍物检测系统。随着机器视觉技术的发展，不仅可以从图像中获取障碍物信息，还可以利用图像实现距离的测量，因此更应该使用机器视觉技术获得更多适合于系统集成的信息。文献[8]预测智能交通系统(Intelligent Traffic System，ITS)可通过机器视觉来感知环境条件。在过去的几年里，机器视觉测距系统也被广泛使用于汽车领域。文献[9]通过安装在车尾的两个摄像头来捕捉立体图像，并进行图像处理，从而计算与后面车辆之间的距离，并将汽车之间的距离数据实时显示给后方车辆。虽然该方法对距离的计算值是准确的，但由于双目摄像头测距算法复杂且标定困难，使得双目测距系统延迟较大。文献[10]使用汽车尾部的单个监控摄像头来对驾驶环境进行分析，通过图像处理计算出与后方车辆之间的相对距离、速度和加速度。但该方法得到的测量量程和测量精度远不能达到城市轨道交通的行驶需求。

本文基于机器视觉提出了一种简单而精确的方法。目前基于单目视觉测距的方法在列车轨道领域还未见报道，并且传统单目测距的方法是利用物体的实际被拍摄面积和该物体在图像中被拍摄的图像面积作比值，从而得出相机与被拍摄物体之间的距离。在列车轨道环境下，利用传统单目测距的算法难以计算其面积特征，所以提出利用轨道的特殊环境，即轨道之间的距离始终为1 435 mm来优化距离计算式。本文经过实验验证了该系统能够在200 m内有效检测前方列车距离，可以满足城市轨道交通安全行驶的要求。

1 轨道检测

为了获得行驶列车前方的信息，在列车车头安装了一个相机。将收集到的视频数据传输到处理单元中，并将图像分割成单帧图片，然后利用卷积神经网络(Convolutional Neural Network，CNN)对图片中的轨道进行有效检测。

该方法包括两个阶段：(1)在第1阶段中，利用卷积神经网络实现轨道环境图像的像素级分类[11-12]。本文的网络主要包括编码层和解码层。编码层包括3个基本单元，其中两个核为3且步长为1的卷积层和一个降采样层为一个基本单元。通过3个最大值池化层得到原图像的1/8尺寸，然后使用空洞卷积增强特征图的感受野，从而对轨道进行有效提取。解码层则使用反卷积层，将1/8尺寸的特征图逐步还原到原始图像的大小。将在反卷积过程中还原的图像分别与编码层降采样所得到的同等尺寸的特征图片进行融合，以提高检测精度。整个过程如图1所示；(2)第2阶段采用多边形拟合方法来优化提取的轨道轮廓[11-14]。将两条轨道始终平行这一特性作为有效的参考信息来优化轨道检测结果。图2是在距离前方列车车尾40 m处采集的数据。通过卷积神经网络对其进行轨道检测，其中图2(a)和图2(b)分别为原始图像和检测图像。

图1 卷积神经网络示意图Figure 1. Schematic diagram of convolutional neural network

(a)

(b)图2 原始图像与检测图像对比图 (a)原始图像 (b)检测图像Figure 2. Comparison between original image and detected image (a) The original image (b) The detected image

在轨道检测实验当中，所有的精度结果都使用平均交并比(Mean Intersection Over Union，MIOU)和平均像素准确率(Mean Average Precision，MAP)来度量。MIOU与MAP的计算式如下

(1)

(2)

式中，k+1为类别的总个数(包含空类)；pii是第i类预测属于第i类的像素数，为真正的数量；pij表示真实值为i，结果被预测为j的数量；pji表示真实值为j，被预测为i的数量；pij和pji分别表示假正像素数和假负像素数。本文使用分辨率为640×360的图像进行预测。在得到预测图像后，将其调整到与输出值相同的分辨率，即可用标注图和预测图求出混淆矩阵，从而进一步对图像进行评估。实验结果显示，该方法的MIOU和MAP分别为98.35%和99.15%，表明该方法可被应用于轨道环境。

由于采集图像的条件有限制，实验无法收集不同气候下的图像数据。为解决这一问题，如图3所示，本文通过合成技术合成了虚拟图像。本文以该虚拟图像作为轨道图像来模拟降雪气候，并验证了检测方法对该天气变化的鲁棒性。结果表明，该轨道检测方法在小雪(包括小雨)条件下仍然可以有效地工作。然而，在浓雾或其他恶劣天气的情况下，该检测方法的性能将受到限制。

图3 雪景图像检测效果图Figure 3. Snow image detection

2 距离公式推算

利用两个轨道始终平行这一计算原则，不仅可以优化轨道的检测，还能简化距离的计算步骤。基于小孔成像原理，建立世界坐标系、相机坐标系、图像坐标系和像素坐标系以及4个坐标系之间的映射关系[15-16]。以标准轨道间距(1 435 mm)为已知数据，推导二维图像的几何关系，从而优化距离测量的推导计算式。

将三维场景通过摄像机投射到二维图像平面上。设置任意点P1在世界坐标系中为(Xw，Yw，Zw)， 在相机坐标系中为(Xc，Yc，Zc)，在图像坐标系中为(x，y)，在像素坐标系中为(u，v)。如图4所示，Ow为世界坐标系的原点；Oc是相机光轴中心与镜头所在平面的交点，将其设置为相机坐标系的原点。图像坐标系与像素坐标系都垂直于相机光轴。P1是世界坐标中的一个随机点，P′2是P1在相机中的成像点，P′2是线段OcP1与图像平面的交点，P2是P′2关于Oc的对称点。

图4 小孔成像模型坐标系Figure 4. Schematic diagram of pinhole imaging model

当世界坐标系中的一个点通过镜头从相机坐标系投影到图像坐标系时，基于小孔成像原理，可以推导出世界坐标系与像素坐标系之间的对应关系

(3)

式中，R为3×3的旋转矩阵；T为3×1的平移向量；0= (0，0，0)T；ax=f/dx；ay=f/dy；dx和dy分别是x轴和y轴上每个像素的物理尺寸；(u0，v0)是相机光轴与像素坐标系相交点的坐标；M1为摄像机的内部参数；M2为摄像机的外部参数。

将世界坐标系的原点设置在相机光轴上，即世界坐标系的Zw轴与相机坐标系的Zc轴在同一条直线上。特征点P1所在平面垂直于光轴，其中d为相机镜头到特征点P1所在平面的垂直距离，由此可以得到R=I，T= (0，0，d)T，P1点的世界坐标为(Xw，Yw， 0)，Zc=d，则式(3)可转换为式(4)。

(4)

由式(4)可以通过像素坐标系中的坐标(u，v)推算出在世界坐标系中相对应的Xw与Yw的比值，如式(5)所示。

(5)

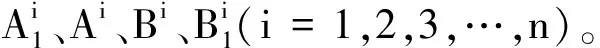
(6)

图5 被测物体面积计算示意图Figure 5. Diagram for calculating the area of the measured object

根据实际物体的正视图面积与照片中图像面积的比值，可以得到检测目标的距离计算式。

(7)

但是在实际中，所拍摄的列车照片的尾部轮廓并不规则，这为检测轮廓以及计算其面积的工作带来了困难，使得研究人员难以从列车尾部得到精准的面积值。不仅如此，随着距离的增加，剖面往往会变得更加模糊，增加了测量系统的测距结果误差。本文通过上述轨道间固定的距离来优化测距计算式，使其更加简洁和精确。

如图6中所示，在检测到的两条列车轨道的最远端两个顶点分别记作A和B，并且构造一个以AB线段为边长，所在平面垂直于光轴的正方形ABB′A′。

图6 列车轨道几何算法示意图Figure 6. Schematic diagram of the train track geometry model

根据实际世界中的AB长度(L)计算虚拟正方形在世界坐标系中的面积，其中L为轨道之间固定的实际距离，数值为1 435 mm。物体的实际面积可以表示为S=L2。该正方形在像素坐标系中的面积可以根据A、B两点的像素坐标进行计算。L′是L在图像上的投影长度，因此L′=uB-uA，S1=L′2。将A、B两点的像素坐标代入式(7)中，就可以得到相机镜头到ABB′A′平面的垂直距离d，如式(8)所示。

(8)

最后，测量相机镜头到自身列车车头最前端的水平距离d′ ，就可以得到自身列车车头最前端到前方列车车尾的准确距离计算式，如式(9)所示。

D=d-d′

(9)

3 相机标定

基于机器视觉测距原理，根据张氏相机标定法[17-18]对采集图像的摄像机的内部参数和外部参数进行标定。首先，对事先准备好的棋盘格标定板进行拍摄，通过多次改变拍摄位置和角度捕捉到几张标定图像。然后，通过OpenCV提取棋盘格图像的角点以获得更丰富的坐标信息，从而对相机进行精准标定，计算出相机的内外参数[15]。其中，

为相机的外部参数。

4 实验结果及误差分析

在1∶1列车轨道模型处，将摄像机放置在距离地面1.5 m处，并使其位于两条轨道的中心。为了保证测量的精准度，在采集数据的过程中需要将相机的光轴与地平面的夹角固定在一个值上，分别在光轴与水平面的夹角为85°、90°和95°拍摄了一组照片，并将3组照片进行处理分析。每组的第1张照片是在距列车尾部40 m处拍摄，然后每向后推移20 m再采集张图像，从而组成距离为40～200 m处的一组数据集。基于上述算法，在光轴与水平面的夹角为90°时所计算的测量距离与实际距离对比如表1所示。

表1 在90°时机器视觉测量结果与实际距离对比

为了进行有效的数据分析，本文还进行了多组对照实验，即光轴与水平面的夹角为85°和95° 的距离测量实验。结果表明，通过机器视觉计算得到的距离精度大于94%，并且测量每张图片的时间成本在40 ms以内。在实际中，火车的制动距离取决于许多因素，包括速度、摩擦、延迟时间、刹车片和制动缸、地理位置、质量分布[17]。根据《铁路技术管理规定》，直线运行的客运列车制动距离应满足以下指标：初始制动速度为160 km·h-1、200 km·h-1和300 km·h-1时，制动距离分别小于1 400 m、2 000 m和3 700 m。因此，根据这些要求可以计算出列车的加速度分别为-0.70 m·s-2、-0.77 m·s-2和-0.94 m·s-2。在城市轨道交通中，列车的普遍运行速度为60 km·h-1，在地铁的制动加速度为-0.70 m·s-2时，制动距离达200 m左右。因此，地铁之间应该保持至少200 m的距离以避免列车追尾。此外，由于图像检测需要时间成本，所以高速运行列车的距离检测滞后。在实际生活中，即使是当前轨道交通的最大速度，也可以以速度600 km·h-1，运算时间0.04 s进行粗略估算。依据此数据可得距离检测的滞后距离<7 m(600 km·h-1×0.04 s =6.7 m)。计算期间产生的滞后距离所造成的误差同样满足列车安全运行要求。

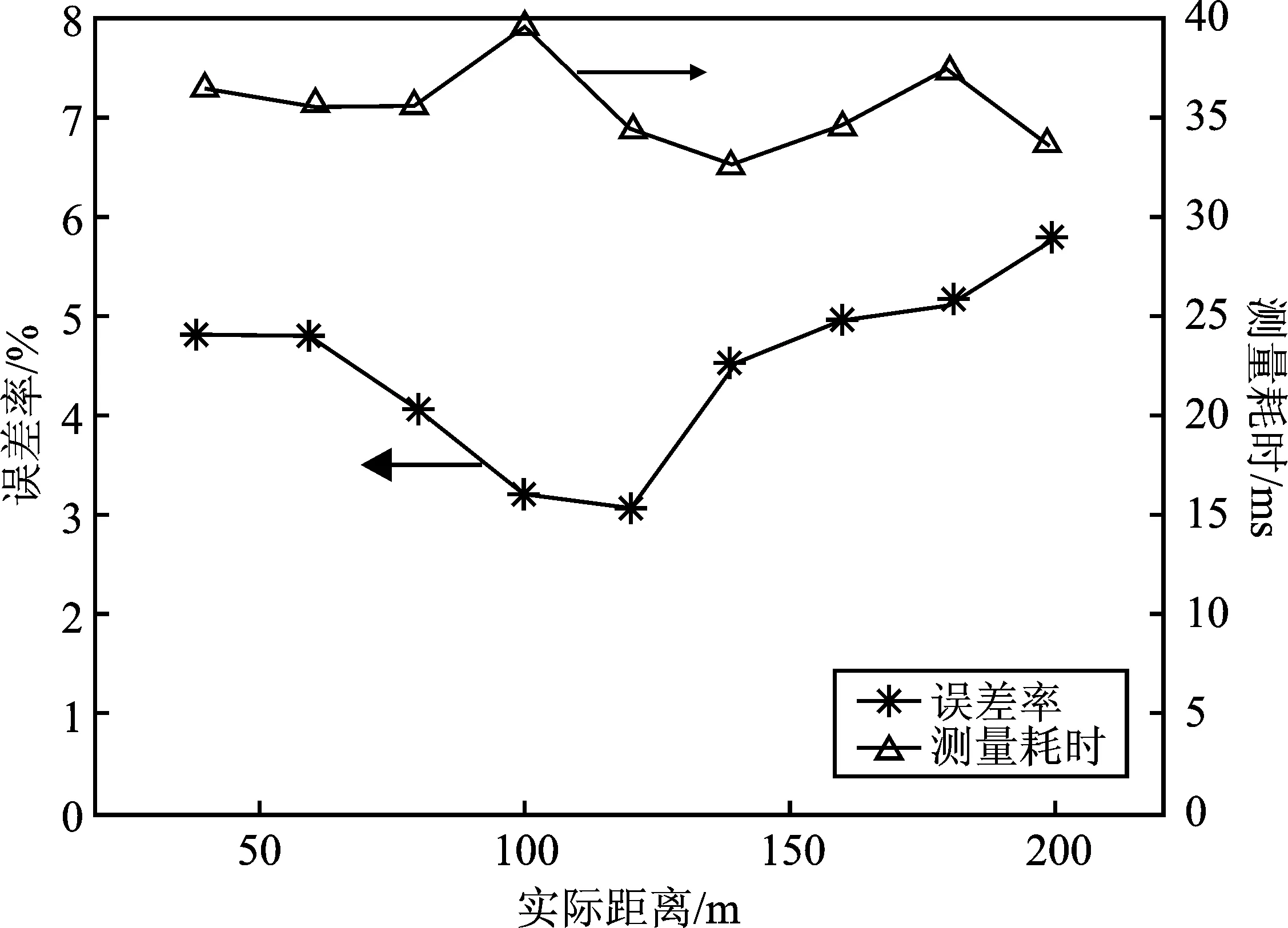
(a)

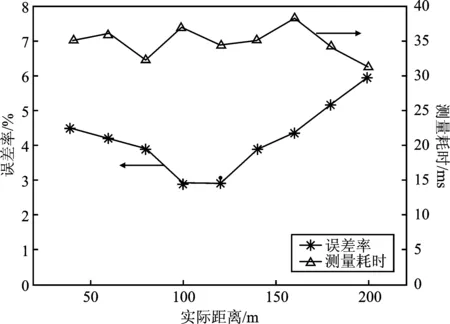
(b)

(c)图7 误差率和测量时间分析图表 (a)85°实验结果图 (b)90°检测图像 (c)95°实验结果图Figure 7. The analysis chart of error rate and measurement time (a) Experimental result analysis at 85° (b) Experimental result analysis at 90° (c) Experimental result analysis at 95°

将3组(85°、90°、95°)所得的实验数据绘制成如图7所示误差率图表。综上分析可知，产生测量误差的主要原因在于两个轨道的中心点位置A、B两点的像素坐标检测。由图7所示误差率所呈现的变化趋势可得，在前方列车距离自身列车距离较小时，所采集到的轨道图片中轨道更为清晰，但是对于检测两条轨道的中心点则产生了更大的偏差，导致距离测量误差率较高；在前方列车距离自身列车距离较大时，虽然图像的分辨率会随着距离的增加而降低，但定位A、B两点的精度却随之变高，使得误差率略微减小；再向更远的距离进行检测时，图像的分辨率对实验结果的影响成为主要因素，导致误差率不断升高。因此，图像分辨率和轨道中心位置A、B两点的检测所产生的误差组合带来了如图7所示的误差波动。当测量过程中相机的角度全程固定在一个合理范围内的值时，对测距结果的轻微影响可以忽略不计。

单目测距的实验通过静态摄影来获取数据集，但即使是在视频数据中，也仍然能够从中提取出清晰图像作为关键帧。因此，在该测距系统中使用的静态图像也可以有效证明此方法能够实现避免列车碰撞的效果。实验证明，实验结论不受相机角度和位置的影响，只要相机在数据采集过程中是固定的，该测距系统至少可以在200 m范围内达到标准。

5 结束语

本文提出了一种基于单目视觉的轨道交通距离测量方法，满足了智能车辆控制的实时性要求。该系统可以有效检测出轨道上运行的前后列车之间的距离，将距离转化成可视化信息呈现给驾驶员，为驾驶员提供报警信号。实验结果表明该系统能够满足轨道交通的需要，保证列车在适宜的气候条件下安全运行。在轨道交通系统中，可以方便地将已知固定轨道空间(1 435 mm)的距离测量与其他图像信息集成在一起进行障碍物检测，实现多功能融合。同时，该方法也是激光或雷达测量距离以外的一种冗余检测。