融合目标速度变化机制的视频摘要生成模型

牛嘉丰，石蕴玉，刘 翔，李任斯

(上海工程技术大学 电子电气工程学院，上海 201620)

监控摄像头已被广泛应用于各行各业，由此也产生了规模庞大的视频数据。传统的视频压缩算法，例如文献[1]根据张量紧凑表示概念提出了张量迭代Tucker-ALS算法，虽取得了较好的效果，但压缩能力有限。为了提高压缩率，基于目标的视频摘要生成方法得到了越来越多的关注。

文献[2]和文献[3]分别提出了融合纹理算法的高斯混合模型和图切割算法，提高了摘要视频中目标的提取效率和质量。文献[4]在时空域中同时移动目标，在充分利用背景空间的同时避免了目标碰撞。但该方法不可避免地破坏了目标间的时序关系，且必须合成与目标匹配的新背景。文献[5]构造了潜在的碰撞图，在该潜在碰撞图的基础上，将减少目标碰撞的问题转化为图着色问题。文献[6]所提出的方法同样是一种基于图的目标重排算法，其用动态图表示目标间的相互关系，并使用动态图着色算法解决了目标重排问题。文献[7]针对目标重排中能量函数的优化问题，首先提出了粒子群优化算法，在提升了能量函数优化速度的基础上减少了目标碰撞。文献[8]提出了目标时空信息分组算法和基于时空信息的摩尔投票算法，获得了目标间的时空交互关系，并进行分组关联，有效避免了目标时序错乱的问题。

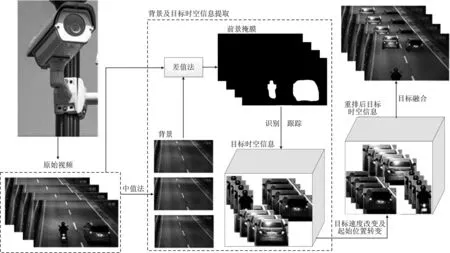
图1 视频摘要生成模型流程图Figure 1. Flow chart of video synopsis generation model

以上工作中，目标本身均保持完整。为了进一步减少目标碰撞和时序错乱，文献[9]提出了缩放目标大小的方法。该方法虽然直接有效地避免了目标间的碰撞，但是目标不能被缩放得太小，否则难以在摘要视频中被分辨出来，而目标的忽小忽大也会影响摘要视频的浏览效果。

本文设计了目标速度变化机制，通过改变目标速度，使得目标避免碰撞，且可以更灵活地进行排列。本文设计了含有速度变量的能量函数，并使用马尔科夫链蒙特卡罗随机采样算法求解了能量函数的最小值，获得了目标重排的最优解决方案。

1 视频摘要生成模型

视频摘要生成模型如图1所示。从原始视频中提取背景图和目标时空信息后，对目标的速度和起始位置进行转变，得到重排目标的时空信息，再将目标融合进背景即可生成摘要视频。

1.1 背景及目标时空信息提取

由于视频背景是不断变化的，因此使用中值法，每两分钟获取一张背景图以应对背景变化[10]。然后，使用背景图和原始视频帧做差，将差值的绝对值大于15的像素点作为前景像素点。最后，使用高斯混合模型[11]和跟踪算法[12-13]对前景掩膜进行识别，并跟踪获取目标ID和时空信息。

1.2 速度变化机制及符号表示

1.3 能量函数

E(S，V)=Ea(S，V)+ωcEc(S，V)+

ωtEt(S，V)+ωdEd(V)

(1)

式中，E(S，V)、Ea(S，V)、Ec(S，V)、Et(S，V)、Ed(S，V)分别代表总能量、活动丢失能量项、碰撞能量项、时序能量项和抑制速度变化能量项；ω*是平衡各能量项的权重参数，其中活动丢失能量项的权重始终为1。

1.3.1 活动丢失能量项

视频摘要需要最大限度地反映原始视频中的内容，因此需要尽可能地保留原始视频中的活动目标信息。活动丢失能量是原始视频中存在的目标没有在摘要视频中出现所造成的损失。活动丢失能量项的定义为

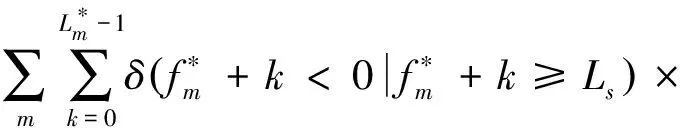
(2)

1.3.2 碰撞能量项

原始视频中的目标重新排列后，原本时空上无交叉的目标很可能出现碰撞现象，从而影响摘要视频质量，因此本文定义了碰撞能量项来抑制碰撞的发生

(3)

式中，m、n取遍所有目标的组合且m≠n；A(·)为面积求取函数。

1.3.3 时序能量项

一般情况下，在原始视频中较早出现的目标在视频摘要中也应该较早的出现。为了惩罚目标经过重排后时序被打乱的情况，并结合目标速度变化对时序造成的影响，本文对时序能量项的定义为

(4)

式中，m、n取遍所有目标的组合且m≠n；D(m，n)为目标m和目标n所形成的时序能量，其定义为

(5)

式中，d(m，n，o)表示目标m和n在原始视频第o帧中掩膜间的欧式距离；依据经验，σ、ω分别取值为10和40；k1、k2分别为两个目标在原始视频中起始帧的最大值和终止帧的最小值，其定义如式(6)和式(7)所示；R(m，n)、T(m，n)的定义则为式(8)和式(9)

k1=max(fm，fn)

(6)

k2=min(fm+Lm，fn+Ln)

(7)

R(m，n)=

(8)

(9)

式中，avg(·)表示其中表达式不为0项求和后的均值。

1.3.4 抑制速度变化能量项

为了使目标速度变化尽可能小，本文定义了抑制速度变化能量项来惩罚目标速度变化大的现象。其定义为

(10)

式中，m取遍所有的目标；ε依据经验设置为2。

1.4 能量函数最小化

由于目标速度是可调变量，而传统优化算法求取式(1)的最优解会较为困难，因此优化算法采用和文献[10]同样的优化策略，即使用马尔科夫链蒙特卡罗(Markov Chain Monte Carlo，MCMC)随机采样算法[14]求解式(1)的最优解。为了使用MCMC算法，首先将式(1)转换为一个玻尔兹曼密度函数

(11)

式中，β是温度常数，本文设置β为1；Z为归一化因子。由于Z的计算比较复杂，因此使用Metropolis-Hastings算法[15-16]以避免计算Z。

初始化解决方案C=(S，V)，随后使用建议分布q(C*│C)生成新的解决方案C*。新解决方案的接受率表述如式(12)所示。

(12)

如果新解决方案被接受，则将当前的解决方案设为C*，否则为C。依次迭代一定次数后，若采集的样本服从式(11)的分布，则选择所有样本中使p(S，V)值最大的解决方案作为式(1)的最优解。建议分布由如下3部分等概率事件组成：

(1)随机选取一个目标，并随机选取摘要视频的一帧作为此目标的起始帧；

(2)随机选取一个目标，并从区间[a，b]中随机选取一个浮点数作为此目标的速度；

(3)随机选取两个不同的目标，并交换这两个目标的起始帧。

由于建议分布是对称的，即q(C*│C)=q(C│C*)，因此式(12)可简化为如式(13)所示的形式。

(13)

详细的算法流程如算法1所示。

算法1 目标重排算法输入:所有目标的原始时空信息和迭代次数Iter。输出:最优配置C。1.初始化一个解决方案C02.n ← 13.max← 04.while n < Iter5. fun ← randint[1,3] //1到3的随机整数6. if fun == 1 //目标起始位置转换7. shift ←randint[1,N]8. C∗( f∗shiftt) ← randint[0, Ls)9. else if fun == 2 //目标速度变化10. speed ← randint[1,N]11. e ←rand[a,b] //a到b的随机浮点数12. C∗(vspeed)← e13. else if fun == 3 //两目标起始位置互换14. swap1 ← randint[1,N]15. swap2 ← randint[1,N]16. tmp ← C∗(f∗swap1)17. C∗(f∗swap1) ← C∗(f∗swap2)18. C∗( f∗swap2) ← tmp19. α ← min(1, p(C∗)/p(Cn-1))20. t ←rand[0,1] 21. if t < α then Cn ←C∗22.else Cn ← Cn-123. if max < p(Cn)24. Cmax←Cn, max ←p(Cn)25. n ← n+126.end while27.return Cmax

1.5 目标融合

本文在目标融合阶段采用泊松编辑算法[17-19]，解决了目标和背景融合时的边缘过渡问题，提高了摘要视频的视觉质量。

2 实验及分析

2.1 实验环境

处理器CPU为AMD Ryzen Threadr-ipper 1900X 8-Core 3.8 GHz，GPU为4×Nvidia GTX 1 080 Ti，内存RAM为64 GB，系统为Windows10。

2.2 测试视频

本文共使用了3个测试视频。前两个来自网络中的公路监控视频，第3个来自于MEVA数据集[18]的广场监控视频。测试视频的详细参数如表1所示。

表1 视频参数

2.3 参数设置

在求取能量函数最优解的过程中，在压缩率要求比较高时，减少某能量项的大小是以增加其它能量项为代价的。由于各能量项的计算数值相差很大，且能量函数总是趋向于使得总能量最小的方向优化，因而容易造成能量项的优化失衡，出现类似目标重排结果中没有时序错乱问题但目标碰撞问题较严重的情况。由此可知，各能量项的权重ωc、ωt和ωd对能量函数的优化过程具有重要的指导意义。

当测试视频1的压缩率设为0.2，且各个能量项的权重均置为1时，能量函数4 000次迭代的总能量及各能量项能量的变化如图2所示。由图可知，总能量、碰撞能量和抑制速度变化能量在1 000次迭代后速度变缓，这是因为随着能量函数的优化，各能量项相互转化的次数变多，而时序能量的数值比碰撞能量和抑制速度变化能量的数值大了几个数量级，所以在时序能量优化到一定程度时，碰撞能量和抑制速度变化能量也很难继续优化。为解决能量项的优化失衡，通过以下步骤选取各能量项的权重：

步骤1选取测试视频并设置压缩率，初始化各能量项的权重为1；

步骤2将能量函数迭代60 000次，并提取总能量变化幅度不超过5%时迭代段所对应的各能量项产生的数据；

步骤3对提取的各能量项的数据分别进行排序，并去除前10%的较大值和后10%的较小值后，对剩余的80%数据求取平均值；

步骤4将步骤3中得到的各能量项的平均值分别乘以权值，其可以使得各能量项平均值的两两比值范围为0.95～1.05。将此权值更新为各能量项的权重，并重复执行步骤2～步骤4直到各能量项权重不再变化。

将3个测试视频依据以上步骤，分别以0.5、0.35、0.2的压缩率调试10次之后，最终设置ωc、ωt和ωd的值分别为1 000、0.001、1 100。章节2.5的对比实验验证了能量项权重设置的有效性。

2.4 评估指标

依据已有研究[5，9]，使用3个评估指标对摘要视频的质量进行评估，所用指标为：(1)压缩率。摘要视频和原始视频长度的比值；(2)碰撞数。摘要视频中目标发生碰撞的对数；(3)时序错乱数。摘要视频中，目标间时序关系和原始视频不同的对数。

2.5 对比实验

本文分别实现了文献[4]和文献[8]的方法，并在测试视频上将这两种方法同本文所提方法进行了对比实验。3个视频的实验迭代次数均为100 000次，实验结果中各评估指标的对比结果如表2所示。实验效果如图3所示，其中图3(a1)、图3(b1)和图3(c1)分别为3个测试视频的原始视频帧。图3中，从图3(a2)、图3(b2)和图3(c2)开始，由左至右分别为本文方法、文献[4]、文献[8]方法产生的摘要视频帧。

(a)

(b)

(c)

(d)图2 能量变化示意图 (a)总能量 (b)碰撞能量 (c)时序能量 (d)抑制速度变化能量Figure 2. Schematic diagram of energy change (a)Total energy (b)Collision energy (c)Chronological energy (d)Limited speed change energy

表2 实验结果

视频1的特点是目标主要出现在右侧两个车道内。当3种方法对视频1的压缩率均为0.21时，从表2的实验结果可以看出，本文方法生成的摘要视频没有发生目标碰撞和时序错乱。文献[4]的方法虽然没有造成目标碰撞，但时序错乱问题最严重。文献[8]的方法同时造成了目标碰撞和时序错乱问题。经分析，文献[8]造成的目标碰撞和时序错乱问题是由于压缩率设置较高导致的。文献[4]的方法在目标重排时改变了目标的空间位置，如图3(a1)中，标黑框的汽车原在中间车道，但文献[4]的方法却使标黑框的汽车出现在了左侧车道上，虽然达到了充分利用空间的目的，并有效避免了碰撞，但容易出现目标时序错乱的问题。本文方法则有效地通过改变目标的速度使得目标排列更加灵活，从而避免了目标碰撞和时序错乱的问题。

视频2的特点是所有目标均匀出现在两个车道内，且目标比较密集。当3种方法对视频2的压缩率均为0.34时，从表2可以看出，本文方法仅造成了1处时序错乱问题；文献[4]和文献[8]的方法造成的目标碰撞和时序错乱程度类似。经分析，由于视频2中几乎没有空闲空间，使得文献[4]的方法改变了目标的空间位置，因此和文献[8]出现了类似的目标碰撞和时序错乱问题。

视频3的特点是所有目标相对于背景比较小，目标轨迹长，且目标出现和离开的位置较多。当3种方法对视频3的压缩率均为0.08时，从表2中可以看出，本文方法造成了1处目标碰撞和1处时序错乱问题；文献[4]的方法没有目标碰撞问题，但时序错乱问题最多；文献[8]的方法同时造成了目标碰撞和时序错乱问题，且目标碰撞问题最多。经分析，虽然视频3的视频场景给了3种视频摘要生成方法足够的应用空间，但压缩率设置偏高，因此文献[8]的方法同时造成了目标碰撞和时序错乱问题。文献[4]中的方法虽避免了目标碰撞问题， 却造成了严重时序错乱问题。本文方法在高压缩率下造成的目标碰撞和时序错乱问题最少，且程度相近。

(a1) (a2) (a3) (a4)

(b1) (b2) (b3) (b4)

(c1) (c2) (c3) (c4)图3原始视频帧及摘要视频帧示意图Figure 3. Diagram of original video frame and synopsis video frame

综上所述，视频1和视频2的对比结果验证了本文方法的有效性和稳定性。基于视频3的对比实验结果不但验证了本文方法的优越性，还验证了各能量项权重参数设置的合理性。

3 结束语

本文将目标起始位置变量和目标速度变量同时融入目标重排的能量函数中，并使用马尔科夫链蒙特卡罗随机采样算法得到了该能量函数的最小值，得到了目标重排方案的最优解。对比实验验证了在相同压缩比的条件下，相较于其他方法，本文方法生成的摘要视频具有较少的目标碰撞和时序错乱问题。今后，将进一步研究能量函数的优化问题，以使优化过程更加高效。