某些特殊用途船舶的稳性计算分析

吴海燕

（广东中远海运重工有限公司，东莞 523146）

1 前言

船舶稳性计算，主要分为完整稳性计算和破舱稳性计算：

（1）完整稳性

是指船舶在各种营运或作业状态下，受外力作用而具有抵抗倾覆的能力。

完整稳性由两部分组成：一是稳性的基本要求，包括气象衡准和复原力臂曲线特征值的要求；二是稳性的特殊要求,即船舶在满足稳性基本要求的前提下，还需要根据船舶的类型、用途、营运或作业特点，考虑受到特定外力作用时的稳性。

（2）破舱稳性

是指船舶在一舱或多舱破损进水后，能继续保持一定的浮性和稳性，使船舶不至于沉没，确保人员和货物的安全性能。

破舱稳性的计算，主要有两种方法：

（1）确定性方法

是规定船舶在纵向、横向和垂向的破损范围，确定一个或多个舱破损的最危险组合；计算出上述破损要求的极限重心高，满足任一计算状态的破损稳性要求。

（2）概率性方法

是规定船舶在纵向、横向和垂向破损的最大范围，考虑该范围内的纵向分隔、横向分隔及水平分隔的作用，不限制破损部位；规定破损浮态、稳性指标与生存概率的关系；根据各种舱组的破损概率以及破损进水后的生存概率计算生存指数，并与要求的生存指数比较，允许某些舱组的生存能力低于衡准的要求。

下面以本公司在建的某牲口运输船以及UT771WP型船为例，具体说明这类型船舶的完整稳性和破损稳性的计算过程。

2 某牲口运输船稳性计算

某牲口运输船完整稳性满足AMSA（澳大利亚海事安全局）对牲口船的特殊衡准要求，其中破损稳性按照概率性破损的要求进行计算。

该船分为12 个装载工况计算完整稳性，见表1。

表1 某牲口运输船装载工况

种装载工况的基本数值，见表2。

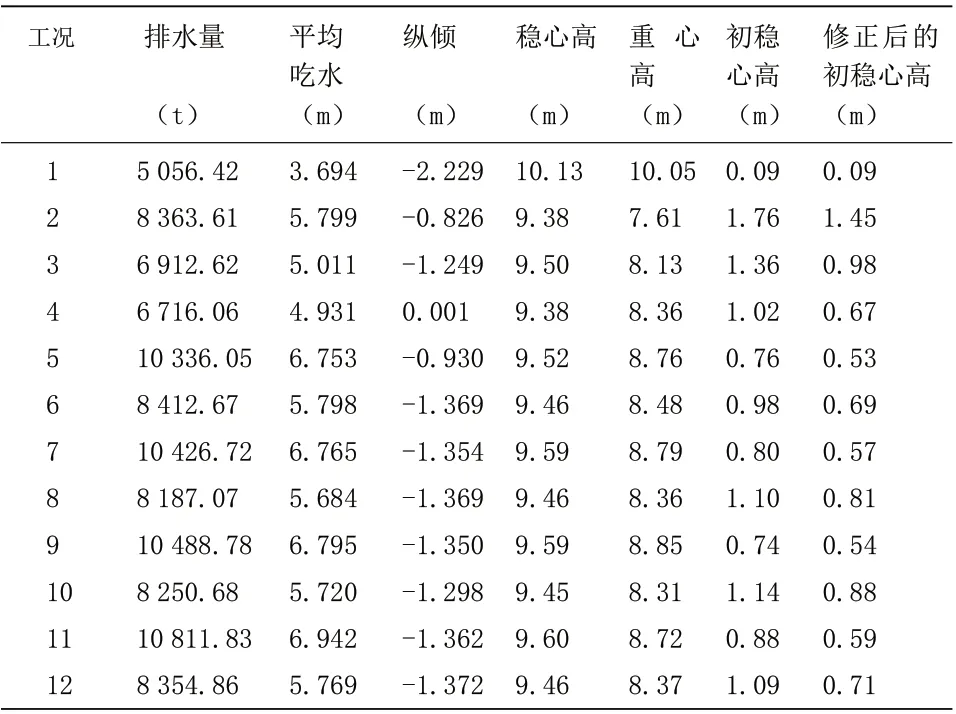
表2 某牲口运输船各装载工况基本数值

该船在非运输牲口的工况，仅需满足IS CODE 对一般货船的稳性要求；但对于运输牲口工况，除了需满足IS CODE 的稳性衡准要求外，还需要满足AMSA对牲口船的要求，主要有横倾角的要求及面积要求。

其中，AMSA 对横倾角的衡准要求比较严格，要求受横风作用时的横倾角度不大于10°，而本船在运牛状态的最大横倾角度达到了9.87°，非常接近衡准要求值。这主要是因为牲口运输船的吃水以上的侧投影面积过大，导致侧向风倾力矩大，因此横倾角度偏大。对于这一点必须特别注意，因上建面积不能更改，应该尽量降低运输牲口工况时的重心高度，使力矩与GZ曲线的交点处对应的横倾角度减小。

牲口运输船是B 型干舷的货船，因此破舱稳性需要满足SOLAS PART 2 中B 部分概率性破损的要求，其分舱指数按照货船的公式计算得到。此外，按照SOLAS 的要求，必须设计三个破舱稳性的计算工况，分别为对应于最深分舱吃水Ds 的工况、轻载航行吃水Dl 的工况、以及在这两种吃水之间的部分装载吃水Dp的工况。三种工况下的破舱稳性总结表，见表3。

表3 某牲口运输船破舱稳性总结表

不同工况对应的GM 值对于概率破舱的生存指数有很大的影响，GM 值越大，生存指数越高；但是GM值偏大，又会反过来影响完整稳性的计算，因此如何在这两种需求中选择合适值，使其既能保证破损稳性的生存指数满足要求，又能满足完整稳性装载以及稳性要求。考虑到本船的概率破损稳性得到的生存指数有较大的余量，因此可以适当降低GM 值，以保证满足完整稳性中更严苛的AMSA 衡准要求。

3 UT771WP 型船稳性计算

UT771WP 型船，既是近海供应船(PSV)又是特种用途船(SPS)，因此其完整稳性必须同时满足近海供应船和特种用途船的要求：按照近海供应船，必须用确定性的方法求得确定区域破损的要求；按照特种用途船，必须使用概率性破损的方法。

船舶根据用途不同，其设计工况是不同的，对于有多种用途的船舶，必须根据不同的设计需求来计算不同的装载工况。此外，在破舱稳性中，因为不同的设计需求，计算的方法也是不同的：近海供应船，按照近海供应船指南中对破舱稳性的要求，使用确定法计算；特种用途船，则根据特殊人员数量不同比照客船的要求进行计算。一般客船的破损稳性计算，均是参考SOLAS PART 2 中B 部分概率性破损的要求，分舱指数是按照客船的要求进行计算的，要求更严格。

该船的破舱稳性总结表，见表4。

表4 特种用途船破舱稳性总结表

从表4 可知：本船的生存指数为0.544 60，而要求的分舱指数为0.542 94.，两者之间非常接近。虽然提高各个工况的GM 值可以提高破损的生存指数，但由于此时完整稳性所用的GM 值已经接近极限值，因此可操作的空间较小。这时需要特别注意空船的重心高度，如果能保证空船的重心高度满足要求，那么完整稳性和破损稳性均有可调整的空间；如果空船的重心高度上升，就会导致概率破损不满足要求，可能需要额外增加各种阀以提高破损工况的生存概率，或是限制船舶吃水或纵倾等，这些措施都会增加经营成本。

UT771WP 型船初步设计时的空船重心高度值为7.50 m，在这种情况下计算的概率破损稳性满足要求，分舱指数为0.542 94，生存指数为0.593 37，尚有较大的余量；但在UT771WP 系列完成首艘船的倾斜试验后，空船的重心高度值增加了25 cm，重心高度值为7.75 m，这时概率破损稳性不能满足规范要求。为此，要求在系列船的泵舱的进风口和出风口处增加两个远程遥控阀。我们比较初步破损稳性计算报告后，发现主要问题可能集中在结构吃水工况的破损，此时吃水较深，破损后可能引起较大的累积进水，导致生存指数大幅度的降低。因此，按照原报告在结构吃水的GM值为1.90 m，但本船在Ds（最深分舱吃水）时的GM 值可以提高到2.05 m，可以提高结构吃水时的生存指数值，因此我们向设计公司提出增加结构吃水时的GM 值重新计算，计算结果见表5。

表5 设计公司第一次修改计算结果

由表5 可知提高Ds（最深分舱吃水）处的GM 值会提高生存指数，按照要求的分舱指数为0.542 94，得到生存指数为0.548 45，满足要求：但是本船是满足SPS（特殊用途船）的要求，其中不仅要求生存指数大于分舱指数，并要求每个装载状态的生存指数与分舱指数比值A/R 大于0.9，本船Dl(轻载航行吃水)和Dp（部分装载吃水）均满足A/R 大于0.9 的要求，而Ds（最深分舱吃水）时A/R 仅为0.87,不满足要求。因此还要考虑别的方法来提高Ds 装载状态的生存指数。考虑到本系列船有8 艘船，每艘船需要增加2 个阀，光增加阀的成本就需要近百万人民币。此外，在泵舱增加阀不仅需要对管路进行大的修改，而且也会占用有限的泵舱空间，船厂和船东都不是很乐意增加这两个远程遥控阀。经过再三考虑，我司技术部在很短的时间内完成了本船稳性计算建模，并将设计公司的各项稳性计算所需数据代入模型中去，经过详细的比对，发现设计公司在两处数据输入有问题，其一为设计公司将除了机舱以外的所有的机器处所设置为空舱，而按照SOLAS 的要求，空舱的渗透率为0.95，机器处所的渗透率为0.85，渗透率的提高会导致各个机器处所的进水量增加，使破损稳性的GZ 曲线降低，稳性更为恶劣；其二是将通往泵舱的两个透气管设计为通海，实际上这两个透气管的管路是先经过1 个油舱再进入到甲板上，直接将其设置为通海就意味着水不是从透气头进入或是油舱舱室破损然后从破损的管道处进入，而是直接从设计管道的某个转折点进入，这显然是不合理的。

考虑到以上两点，我们修改了稳性计算输入数据，结果表明，上述任何一点的改变都会大幅提高破损的生存指数。为此，将以上两点反馈给设计公司，并付上我们的计算结果后，除了第一点设计渗透率是船级社要求，以便更严格考察带SPS 要求的稳性外，设计公司承认了自己第二点的计算错误，并免费更改了整个计算，重新得到计算结果（见表6）。

表6 第二次修改计算结果

由表6 可以看出，修改了伸往泵舱的透气管的走向，生存指数就得到显著的提高，生存指数从0.548 45提高到了0.550 24；Ds 装载状况时的生存指数与分舱指数比值A/R 也得到大幅度的提高，A/R 值从0.87 提高到了0.97，这是因为Ds 吃水最大，然后很容易通过此前的透气管的通海口进入到泵舱，导致生存指数降低。

4 结束语

本文以某牲口运输船和UT771WP 型船的稳性计算为研究对象，对这两种特殊用途船型所需要满足的稳性要求进行分析，并详细描述了这两型船舶满足确定性破损以及满足货船和客船的概率性破损的要求的计算过程。本文的分析过程，对类似的特殊用途船型的稳性计算提供了一定的参考，同时也为如何提高破损稳性生存概率的方法提供了一定的参考与借鉴。