MEFP协同冲击平面带壳装药数值模拟研究
2022-09-13刘永旭赵长啸杨善平张昌旺
张 琨,刘永旭,赵长啸,唐 蓉,杨善平,张昌旺
(陆军工程大学,南京 210007)
1 引言
冲击毁伤近程来袭弹药目标,对于低空反导、维护空域安全等具有重要意义。应用具有一定密集分布的破片群束撞击是较为有效的方法,其本质是破片的冲击起爆问题。针对冲击起爆问题,国内外专家学者聚焦单破片的冲击作用进行了大量系统性研究;在此基础上,一些学者也向多破片冲击起爆平面装药方向进行研究。杨洋等采用Lee-Tarver点火与增长模型,研究双钨球同时撞击柱壳装药的冲击起爆规律,发现叠加冲击波压力峰值及其持续时间均会产生影响。李文彬等研究了双破片非同时命中和同时命中裸药问题,发现冲击波的累积叠加作用对冲击起爆具有较大影响。梁斌等采用“升—降”法研究了多破片同时或间隔作用情况下的冲击起爆规律,获得了B炸药的起爆阈值。郭淳等综合考虑钨球个数、空间碰撞位置分布及时间间隔等因素,通过数值模拟获得了柱壳装药的起爆速度阈值。贾宪振等通过数值模拟对多破片撞击平面装药问题进行研究,得到了起爆速度阈值的变化规律。王昕等分析破片命中位置和装药曲率半径双因素耦合作用下对柱壳装药冲击起爆效能的影响规律。
根据公开文献报道,现有研究破片通常是正方体、六棱柱和球体等理想化规则体且简化为刚体特性,与真实毁伤元相比无论形态特征还是综合性能均存在差异。破片的复杂现实工况必须予以充分考虑并开展深入细致的研究。多爆炸成型弹丸战斗部又称MEFP,是Multiple Explosively Formed Penetrator的简称,可产生具有一定密集度的高速弹丸同时对目标实施攻击,具有更强更优的毁伤效能,可极大提高打击毁伤概率。基于此,拟采用ANSYS/LS-DYNA动力学数值计算软件,通过改变组合式MEFP子装药间距调整EFP(explosively formed penetrator)群束密集度,设定多种平面装药壳体厚度以确定计算工况,揭示多弹丸协同冲击不同厚度平面带壳装药的冲击起爆规律,为实践应用提供理论参考。
2 仿真模型建立
2.1 计算模型
组合式MEFP战斗部装药结构,主要由多个子EFP战斗部、填充材料、壳体等组成。独立的子EFP战斗部又包括药型罩、装药、壳体、起爆装置等。本文所研究的组合式MEFP战斗部由7个子EFP战斗部组成,其具体分布为1枚子EFP战斗部位于装药结构中心,其余6枚均匀分布在中心EFP战斗部的四周,结构如图1所示。

图1 组合式MEFP战斗部结构示意图Fig.1 Schematic diagram of the combined MEFP warhead
组合式MEFP战斗部模型和有限元模型具体尺寸分别如图2(a)、(b)所示,由于战斗部结构具有对称性,为节省计算时间选用1/2模型进行求解。战斗部相邻子EFP战斗部间距与周边EFP战斗部距外侧壳体距离相等同为,相邻弹丸径向距离为,战斗部高度为50 mm,口径随变化。战斗部壳体材质为6063铝合金厚度为4 mm;战斗部的填充物为聚氨酯泡沫。7枚子装药均采用同尺寸独立EFP战斗部设计,EFP战斗部装药结构、参数材质和网格单元与文献[13]一致。

图2 有限元计算模型示意图Fig.2 Section view of finite element calculation model
对于组合式MEFP战斗部,弹丸群束的密集程度直接受相邻子EFP战斗部间距与周边EFP战斗部距外侧壳体距离间距影响决定。子EFP战斗部起爆后形成的爆轰波会随间距的变化而受影响,当太小时爆轰波会相互干扰叠加,爆轰波结构受冲击挤压导致弹丸不能平行飞行;当太大时可有效避免爆轰波相互干扰,但最终形成的弹丸群会更加稀疏,不利于提升总体冲击起爆效能。经过大量理论计算及预仿真模拟,选定的值从2 mm变化到8 mm,每间隔2 mm设定一种数值计算工况,按顺序计为工况1至工况4,具体见表1。

表1 4种计算工况设计Table 1 4 calculation conditions
2.2 仿真计算参数
6063铝合金采用*MAT_JOHNSON_COOK材料模型,填充物聚氨酯泡沫采用*MAT_PLASTIC_KINEMATIC材料模型,相关参数见表2,表3。本文所有计算均采用cm-g-μs单位制。

表2 6063铝合金**MAT_JOHNSON_COOK材料模型主要参数Table 2 Main parameters of material model

表3 聚氨酯泡沫*MAT_PLASTIC_KINEMATIC材料模型主要参数Table 3 Main parameters of material model
MEFP战斗部攻击平面带壳装药模型图如图3(a)和立体示意图如图3(b)。平面壳体装药的钢壳体为45钢,背后贴敷的被发装药为TNT厚度为10 mm。为缩短计算时间,设定MEFP战斗部与45钢壳体的作用距离为400 mm。本文中45钢和TNT的材料参数选取和计算模型均与文献[13]中相同。

图3 组合式MEFP战斗部攻击平面带壳装药模型Fig.3 Combined MEFP warhead attack plane shell charging model
2.3 不同工况弹丸群束性能分析
分别对工况1、2、3、4进行数值计算,得到各工况下最终稳定成形的MEFP形态,如图4所示。表4为不同工况下MEFP的性能参数,表中为弹丸质量,为弹丸长度,为弹丸头部直径,表示相邻弹丸径向距离,、分别为弹丸轴向速度和径向速度。通过对比分析,尽管4种工况下MEFP形态近似一致、弹丸直径与长径比也接近一致,但整体的结构分布仍有细微差别。其中工况1各弹丸径向距离最短,为3.76 cm,弹丸分布相对其他3种工况更加密集;工况4弹丸径向距离最长,为4.21 cm,弹丸分布相较其他3种工况略稀疏。

图4 各工况下151 μs时刻组合式MEFP形态图Fig.4 Combined MEFP morphology at 151 μs

表4 不同工况MEFP性能参数Table 4 MEFP performance parameters under different working conditions
由数值计算结果可知,工况2、3、4弹丸速度几乎一致,工况1的中心弹丸和周边弹丸速度偏高于其他3种工况,主要因为子EFP战斗部间距太小装药爆炸时爆轰波发生了叠加作用,总体冲击载荷较大,导致此工况下的药型罩微元所受冲量略高于其他工况。一般而言,MEFP装药结构所形成的EFP群束在飞散过程中将存在一定发散角如图5所示,而发散角大小将直接决定其对目标打击面积。

图5 弹丸发散角(a)及攻击平面示意图(b)Fig.5 Projectile divergence angle and attack plane
由图5可知弹丸的发散角为

(1)
式中:为周向弹丸的发散半径,即=时弹丸径向位移,为=时弹丸轴向位移。且有

(2)

(3)
根据图5(b),弹丸对于目标的打击面积在理论上接近圆形,其面积为
=π
(4)
综合表1中、数据,求得4种工况下最大发散角为0003°,可近似忽略不计,表明4种工况下所形成的弹丸群束平行运动。
3 对平面装药冲击起爆影响研究
3.1 计算结果分析
确定平面带壳装药壳体厚度分别取10 mm、12 mm、13 mm三组数值,此时4种计算工况各对应3种厚度,分计为工况1-1、1-2、1-3,2-1、2-2、2-3,3-1、3-2、3-3,4-1、4-2、4-3。首先,以工况2-1(子EFP战斗部间距=4 mm,平面装药壳体厚度为10 mm)为例研究分析组合式MEFP对平面带壳装药的冲击起爆过程。
根据数值计算结果,=181.9 μs时刻所有弹丸同时开始冲击45钢壳装药,在撞击点周围迅速形成塑性变形区和高压区,并在弹丸头部产生强冲击波;=186.1 μs时刻随着侵彻深度不断增加,弹丸出现速度衰减;=188.2 μs时刻多弹丸撞击在TNT中形成的冲击波相互叠加形成高于起爆阀值的压力峰值达到TNT的临界起爆压力点10.4 GPa,TNT内部出现热点;=188.2~189.9 μs范围时,TNT内部峰值压力出现明显波动,表明此时压缩形成的热点还不够稳定;=191 μs时刻之后TNT内部峰值压力稳步攀升,意味着TNT被成功冲击起爆并稳定爆轰,冲击过程如图6所示。图8为该工况EFP群束冲击起爆钢壳时,被发装药TNT的爆轰波阵面峰值压力变化曲线,详细记录了各时刻TNT内部峰值压力变化情况。

图6 工况2-1组合式MEFP冲击10 mm厚钢壳装药及起爆被发装药过程云图Fig.6 Combined MEFP impact charging process of 10 mm thick steel shell and initiation charging process
为详细分析不同工况下EFP群束的冲击起爆能力,对4种工况下EFP群束冲击平面钢壳装药过程进行数值计算,图7是4种工况EFP群束冲击起爆10 mm厚钢壳被发装药TNT的爆轰波阵面峰值压力曲线,图8是工况2-1EFP群束冲击起爆10 mm厚钢壳被发装药TNT的爆轰波阵面峰值压力曲线。图7和图8的数据都是从EFP群束接触钢壳瞬间开始记录。

图7 4种工况TNT爆轰波阵面峰值压力曲线Fig.7 Peak pressure of TNT detonation wave front in 4 working conditions

图8 工况2-1被发装药爆轰波阵面峰值压力曲线Fig.8 Peak pressure of charge detonation wave front is charged in condition 2-1
通过对比分析,工况1-1的弹丸最先冲击侵彻钢壳体,被发装药TNT达到临界起爆点后内部峰值压力迅速攀升进入稳定爆轰阶段,峰值压力最终稳定在21.2~23.2 GPa。
工况2-1与工况3-1的TNT爆轰波峰值压力曲线基本重合,表明2种工况的冲击起爆能力较为一致。由图8可知,TNT临界起爆点时刻明显早于钢壳被EFP群束穿透时刻,表明TNT率先被弹丸撞击钢壳产生的强冲击波冲击起爆,钢壳在弹丸侵彻和炸药冲击双重作用下被穿透。相比前3种工况,工况4-1的冲击起爆过程较为复杂:在188~200.6 μs范围内钢壳体未被EFP群束穿透,此时主要是弹丸撞击钢壳产生的强冲击波冲击被发装药TNT,虽然装药内部峰值压力个别时刻达到临界起爆压力点,但峰值压力波动非常明显,热点不够稳定集中;在200.6 μs时刻钢壳被弹丸侵彻击穿,得益于残余弹丸与钢壳体破片的共同冲击被发装药TNT被成功冲击起爆并持续稳定爆轰。
按照Howe提出的射弹引爆带壳炸药两种机制进行区分,本算例中工况1-1、2-1、3-1的EFP群束对平面带壳装药作用属于冲击引爆机制,工况4-1的EFP群束对平面带壳装药作用属于剪切引爆机制。本算例中,属于冲击起爆机制的3种工况对TNT的冲击起爆时间明显少于属剪切引爆机制的工况4-1,表现出相对较强的冲击起爆能力。
为对比EFP群束与单EFP的冲击起爆能力差异,仍先以工况2-1为例求解单个周边EFP对目标的冲击侵彻作用。由于EFP群束中单EFP性能趋同,任意选取单EFP进行研究。图9是工况2-1周边EFP单独冲击侵彻平面带壳装药时被发装药爆轰波阵面峰值压力曲线。通过分析发现,周边EFP在200.6 μs时刻侵彻击穿钢壳,这与EFP群束侵彻作用时的击穿时刻相同;在202.2 μs时刻即钢壳被击穿后TNT内部峰值压力才达到临界起爆点,比图8中的临界起爆点时刻延迟了14 μs,冲击起爆所需时间相应增长;与同工况的EFP群束对带壳装药冲击引爆机制不同,本工况下单EFP对带壳炸药的冲击引爆机制属于剪切引爆机制。由此可得,工况2-1的EFP群束具有明显优于单EFP的冲击起爆能力,EFP群束冲击目标过程中表现出较强的协同作用。经过数值计算,工况1-1、3-1的EFP群束在冲击目标过程中同样表现出明显协同作用,冲击起爆能力均强于单EFP。

图9 工况2单EFP作用下爆轰波阵面峰值压力曲线Fig.9 Peak pressure of detonation wave front under single EFP in working condition 2
图10为工况4周边EFP单独冲击侵彻平面带壳装药时TNT爆轰波阵面峰值压力曲线。通过对比图7中的工况4-1和图10,EFP群束冲击平面带壳装药的起爆过程与单EFP作用时基本一致,此工况下EFP群束的冲击起爆能力与单个EFP趋同不再具备协同增强作用。
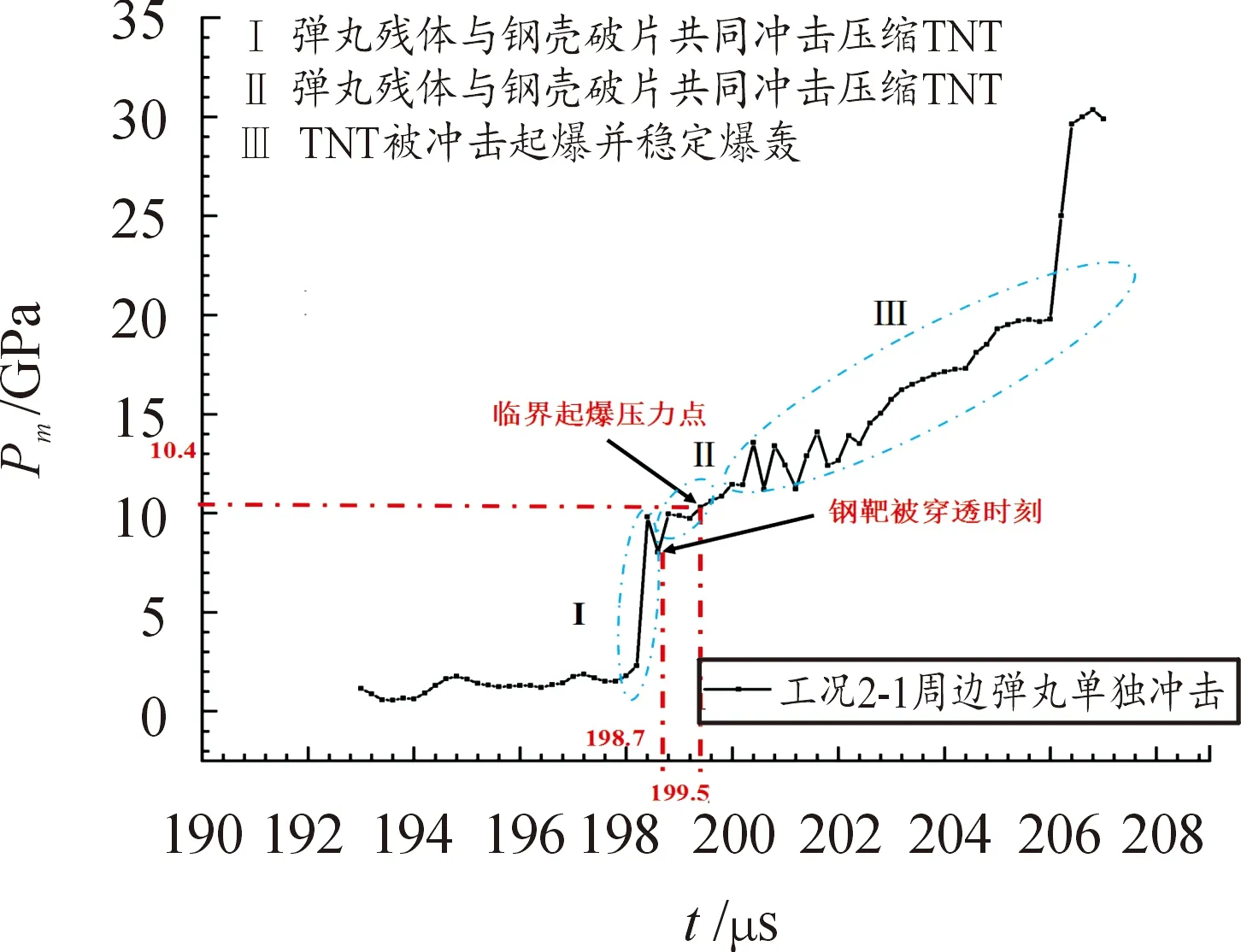
图10 工况4单EFP作用下爆轰波阵面峰值压力曲线Fig.10 Peak pressure of detonation wave front under single EFP in working condition 4
将45钢壳厚度调整为12 mm,通过数值计算得到4种工况(工况1-2,2-2,3-2,4-2)的组合式MEFP战斗部均能成功冲击起爆壳体装药且EFP群束的冲击起爆能力趋于单个EFP,未表现出多弹丸冲击起爆能力的协同增强作用。调整45钢壳厚度为13 mm,经过数值计算,工况1-3的组合式MEFP战斗部可以冲击起爆带壳装药,但单EFP无法冲击起爆;其余3种工况的组合式MEFP战斗部,无论是EFP群束还是单EFP作用时,均无法冲击起爆带壳装药,主要原因是工况1的EFP群束更加密集,得益于撞击产生的叠加冲击波及弹丸的共同挤压作用,平面钢壳装药被成功起爆。不同工况对45钢壳平面装药冲击毁伤结果见表5。
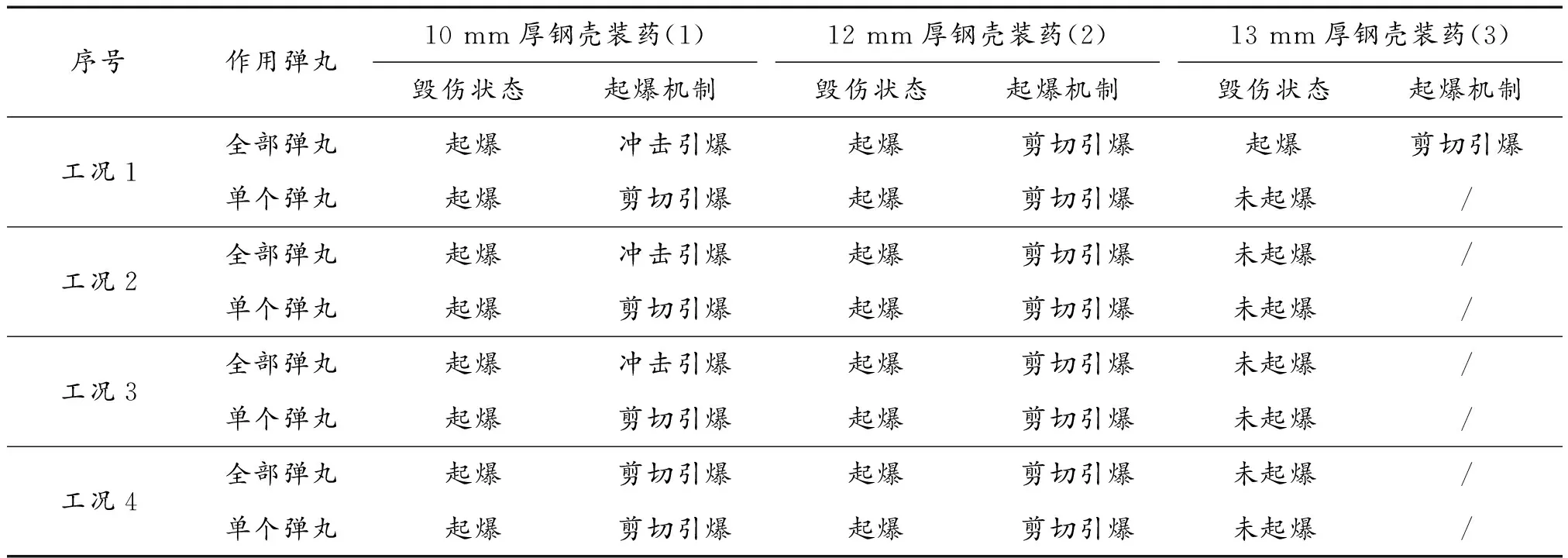
表5 不同工况对45#钢壳平面装药的冲击毁伤结果Table 5 Impact damage results of 45# steel shell plane charge under different working conditions
4 结论
1) 工况1、2、3的EFP群束侵彻10 mm厚钢壳装药具有协同增强作用,TNT成功冲击起爆且冲击起爆用时少于单个EFP冲击起爆用时。
2) 随着各弹丸间距增加,EFP群束协同撞击形成的冲击波衰减,工况4不再具备协同增强作用,TNT无法冲击起爆。
3) 对于12 mm厚45钢壳,TNT仅能在剪切引爆机制下冲击起爆,各工况EFP群束的冲击起爆能力与单个EFP趋同,协同增强作用不明显。
4) 对于13 mm厚45钢壳,仅工况1的EFP群束能够成功冲击起爆,属剪切引爆机制,表明弹丸间距对EFP群束协同增强具有较强关联作用。
