PPP模式下老旧小区改造项目参与主体的利益分配研究
2022-09-12李艳,孙磊
李 艳,孙 磊
吉林建筑大学 经济与管理学院,长春 130118
《关于全面推进城镇老旧小区改造工作的指导意见》(国办发〔2020〕23号)中指出,完成2000年底以前建成的老旧小区改造是“十四五”期末要完成的工作指标之一.城镇老旧小区的改造不仅可以扩大投资需求和消费需求,还有助于建立资源循环型经济:从宏观经济角度出发,老旧小区地改造能扩大内需,并且降低产能过剩,是我国经济新常态下稳定经济增长的重要战略策略;从工业经济角度出发,老旧小区的改造有利于产业结构调整,为建筑业和服务业等产业创造持续效益,具有显著的经济效益和社会效益.但由于老旧小区改造资金需求大、公众参与度不高等原因致使改造呈现出不可持续的结果.对此,国家发改委、住建部联合发布《关于加强城镇老旧小区改造配套设施的通知》(发改投资〔2021〕1275号)中提出,鼓励老旧小区改造运用PPP模式.
1 PPP模式下的老旧小区改造
1.1 PPP模式下的老旧小区改造
当前,老旧小区改造作为推进城镇化的首要任务之一,由于业主对政府的习惯性依赖、政府缺乏专业经验、改造资金需求大等问题导致整体改造进度缓慢.对此,国家发改委和住建部提出使用PPP模式,鼓励社会资本参与投资地方政府设立的老旧小区改造项目.PPP 模式实质就是鼓励政府和社会资本共同运行项目,让社会资本更多地参与到项目中,这样不仅利于解决融资难题和技术瓶颈,同时还能发挥政府的规划作用和市场的机制作用,提高项目的服务水平和工程质量.然而,PPP 模式下的老旧小区改造还存在一个关键的问题,即各方利益分配.PPP模式要求各参与主体"风险共担、利益共享和全程合作",小区业主作为产权人和受惠群众,与政府、社会资本构成了三方合作的利益格局.因此,本文以利益分配研究为重点,旨在最终构建出一个合理的利益分配模型.
1.2 国内研究现状
针对老旧小区改造,学者们展开了以下研究:王克强等[1]人提出在城镇化进程中采用PPP模式不仅扩大了资金来源,并且强化了政府监督职能,有利于实现工程建设的质量;黄珺、孙其昂[2]提出缺乏物质报酬和精神奖励会造成居民主动参与程度低进而影响老旧小区治理;唐龙[3]研究了旧区改造中利益相关者的交互参与模式,发现在旧区改造中利益相关者所占权重前3名的分别为:政府部门、旧区居民、参与的金融机构;樊舒舒[4]通过仿真模型探究了在政府的宣传措施、激励措施和响应措施下,居民参与度的变化,最终实现居民参与度和老旧小区改造的同步提升;赵琰等[5]人在研究PPP模式下的城镇棚户区改造项目利益分配问题时改进了Shapley值算法,该模型对PPP模式下城镇棚户区改造决策具有重要的参考价.
综上,老旧小区的改造属于社会系统工程的范畴,其中主要参与主体政府机构、社会资本、小区居民,只有三者达到整体最佳合作状态才能实现改造利益最大化.然而,鲜有学者研究居民参与老旧小区改造利益的分配,由于老旧小区改造项目带来的社会效益、生态效益等难以衡量,多数学者在使用Shapley值算法进行利益分配时都先假定项目的预期收益是可以准确估计的,这显然与老旧小区改造的真实情况不符.基于上述分析,本文以PPP模式下的老旧小区改造利益主要参与者中的分配问题为研究对象,以合作博弈和区间模糊Shapley值为研究方法,综合考虑风险承担比例、资源投入比例和配合程度3个因素影响,构建适用于PPP模式下老旧小区改造项目中政府、居民和社会资本方的利益分配模型.
2 构建PPP模式下老旧小区改造项目利益分配初始模型
PPP模式下老旧小区改造项目的利益分配本质上是一个多人合作博弈问题,而Shapley值法可以计算n个主体通过合作取得最大收益后的最大利益分配,成为解决多人合作博弈的有效方法.
(1) Shapley值法模型概念. 假设n个不同的成员i构成项目集合I,表示为I={1,2,…,n},其中合作以前每个成员的收入为V(i);成员们通过合作获得一定的总收益Φ(v)时,联盟将总收益分给每个参与成员.同时满足以下3个条件时Shapley值法才具有效应:
(1)
Φ(u)=∑U(i),i=1,2,…,n
(2)
φi(u)≥U(i)
(3)
式中,φi(v)为Shapley值,即联盟成员i所获得的利益;等式(1)是指联盟的总收益须等于联盟单个成员收益总和;等式(2)表示联盟的总收益大于每个成员合作以前收益的简单总和;等式(3)是指成员i在联盟分得的收益要高于成员合作以前的收益.
(2) 三角模糊数概念. 三角模糊数具有计算简单、使用方便等优点,能有效提高模糊环境中模糊信息的表达和处理,故本文将其引入模型构建.关于三角模糊数的定义、计算如下:
若α=(α1,α2,α3),α3≥α2≥α1≥0,则称α满足三角模糊数条件,其隶属函数Vα(x)表示为:
式中,α2为α的中心值;α1,α3为上下限值;α3-α2和α2-α1为三角模糊数的扩散半径.
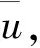
综上所述,Shapley值法确定成员i在所有成员均合作的情况下获得的收益分配值为:
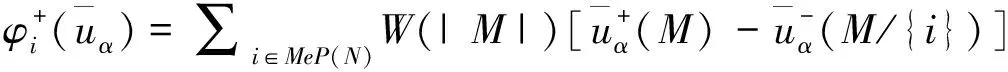
(3)
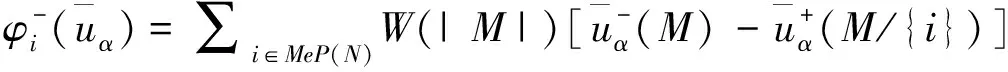
(4)
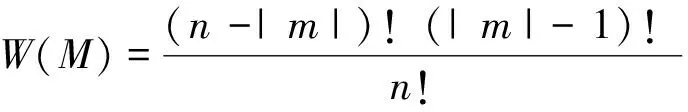
(5)
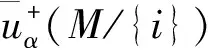
3构建PPP模式下老旧小区改造不确定AHP-Shapley值的修正利益分配模型
3.1 Shapley值的影响因素
(1) 参与主体的投入比重. PPP模式下老旧小区改造项目在居民承担一定费用的前提下,政府部门为妥善处理资金不足问题,选择注入政府资金和邀请社会资本方加入与居民共同持股对老旧小区进行改造.资金投入是项目实施的前提,一般来说,资金投入和利益呈正相关关系,资金投入越多,则期望的回报也越多.资本的性质是追求利润,各方投资的目的都是为了让投入资金提质增值.老旧小区的项目投入主要考虑各方的资金投入、设备投入、技术投入等,将其一并转入货币形式计算投入比重.
(2) 参与主体的风险承担比例. 通过问卷调查和查阅资料,总结出老旧小区改造过程中政府、居民和社会资本各自承担的风险因素,如表1所示.
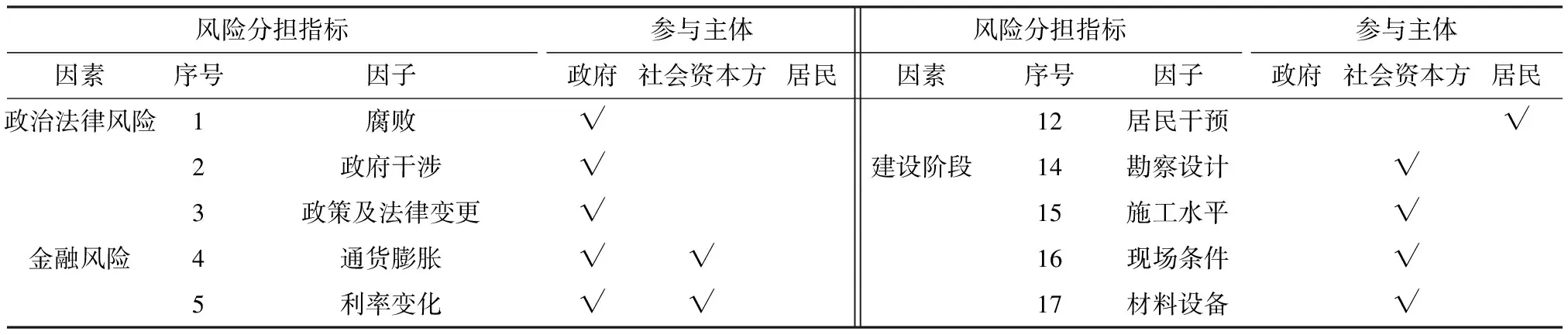
表1 PPP模式下老旧小区改造项目中参与主体的风险分担因素Table 1 Risk sharing factors of participants in the old community reconstruction project under PPP mode

续表1
(3) 参与主体的配合程度. PPP 模式下老旧小区的改造只有建立在合作的基础上,才能将政府部门的社会责任、长远规划和居民对老旧小区改造的决策优势,以及社会资本的资金优势和管理效率结合到一起发挥最大效益.反之,如果在项目的实施过程中,参与方不积极主动的发挥自身优势,不配合项目实施,必然会影响项目的综合改造效益.所以,为了顺利推进PPP模式下的老旧小区改造,激励各方共同合作,还应考虑将 PPP 项目各参与方的配合程度.
3.2 计算影响因素的权重区间
Shapley值法的核心思想是强调价值贡献,于是初始条件便假设各参与主体的投入比重、风险承担、配合程度等影响因素相同,而仅从价值贡献率的角度考虑参与主体的利益分配,事实上该假设是不成立的.所以,为了更全面地研究PPP模式下老旧小区改造项目的利益分配,有必要改进Shapley值法,根据投入回报原则、风险补偿原则、配合度的激励原则对其进行修正.但由于收集有效的综合评分表存在一定困难,并且打分专家因年龄、性别、职业、学识水平等因素引起的认知偏差,在一定程度上会导致权重计算结果不完全具有客观性.鉴于此,本文使用不确定AHP,以模糊区间值削弱专家之间的主观差异,这样可以有效降低主观因素对指标权重的影响.详细步骤如下:
(1) 计算区间数判断矩阵
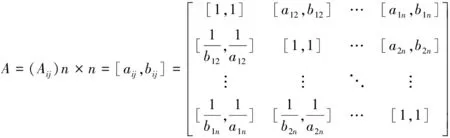
(6)
其中,aij表示专家评判值中的最小值;bij表示专家评判值中的最大值.
(2) 计算权重区间
① 由区间数判断矩阵A得到一致性逼近矩阵M=(mij)n×n
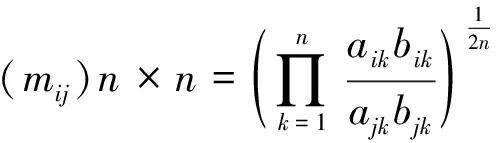
(7)
② 计算M的权重Wi(w1,w2,……,wn)
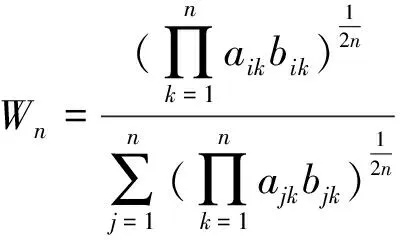
(8)
③ 计算极差矩阵ΔM1,ΔM2和权重传递误差ΔkWj,即:
Δ1M=Δ1mij=(mij-aij)n×n
Δ2M=Δ2mij=(bij-mij)n×n
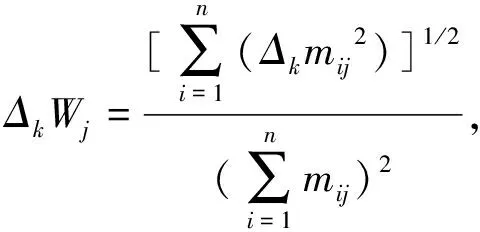
(9)
则区间数判断矩阵A的权重区间:
W′=(W1′,W2′,…,Wn′)
Wj′=(wj-Δ1Wj,wj+Δ2Wj)
(10)
(3) 计算精确的权重值. 通过即对分析理论将权重区间转化为精确权重值,分别从反、异、同3个角度将区间[0,1]划分为[0,wj-Δ1Wj],[wj-Δ1Wj,wj+Δ2Wj],[wj+Δ2Wj,1]3个子区间,Wj与区间[0,1]组成集对后的联系度表达式为:
uj=aj+bji+cjj
(11)
aj=wj-Δ1Wj
(12)
bj=Δ1Wj+Δ2Wj
(13)
cj=1-wj-Δ2Wj
(14)
其中,i,j为差异系数和对立系数.则区间相对权重Pj和模糊相对权重Qj为:
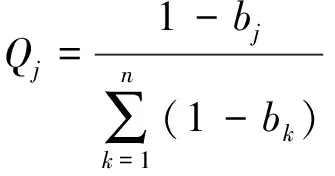
(15)
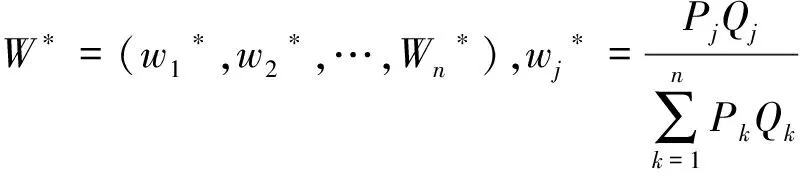
3.3 构建修正利益分配模型
在Shapley值的基础上综合考虑风险承担比例αi、资源投入比例βi和配合程度γi对利益分配的影响,建立修正因子矩阵Ri=[αi,βi,γi],其中:
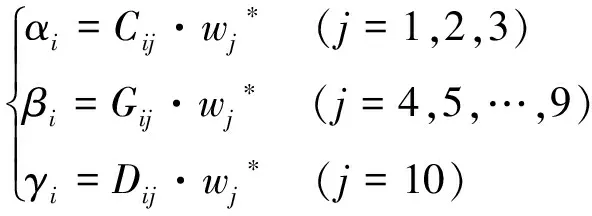
(16)
式中,Cij,Gij,Dij表示风险承担比例α、资源投入比例β和配合程度γ的一级评价指标的权重向量.
通过不确定层次分析法推算出利益分配3个影响因素的权重,并且运用下列公式
πi=w*×RiT
(17)
综合考虑3个因素的影响程度系数πi,对初始模型下的影响程度系数进行修正,获得修正后的区间模糊Shapley值:
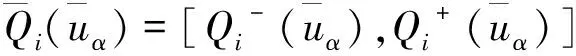
(18)
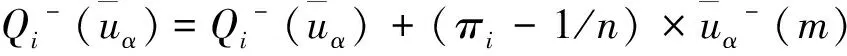
(19)
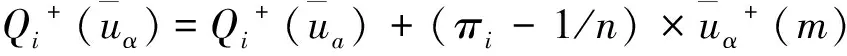
(20)
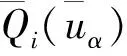
通过以上分析,得到PPP模式下老旧小区改造项目利益的改进利益分配方案.
4 结论
本文以“老旧小区改造项目”为出发点,分析了老旧小区改造的现存问题,为解决改造资金及专业技术等问题提出运用PPP模式;指出改造项目的利益应由政府、居民和社会资本方共同分配,并且构建了政府、居民和社会资本共同参与区间模糊Shapley值的项目利益分配初始模型;
在初始利益分配模型的基础上,以参与主体各自的风险承担比例、资源投入比例和配合程度共同作为利益分配影响指标,运用不确定AHP对初始利益分配模型中的指标权重进行修正,构建了改进Shapley值理论上的利益分配模型.
因本研究是从理论层面进行阐述,所研究的利益分配模型具有一定的外部效应,难以准确计量.因此,如何不断优化与完善这一利益分配方案将成为今后努力的方向.
