基于EWT的离心压缩机出口动态压力单重分形特征研究
2022-09-09刘雁李宇宸耿金成肖军
刘雁, 李宇宸, 耿金成, 肖军
1.西北工业大学 机电学院, 陕西 西安 710072;2.合肥通用机械研究院 压缩机技术国家重点实验室 , 安徽 合肥 230031
当离心压缩机发生喘振时,会引起机组的剧烈振动,并在短时间内造成压缩机部件的严重损坏。为此,科研人员做了大量的研究工作来预防和避免喘振的发生[1]。
目前,常用的方法是通过测试压缩机出口处压力和压缩机的喉部压力差来判断压缩机是否工作在安全区内,这种方法相对可靠并且较容易实现[2]。研究显示,压缩机出口处动态压力信号属于非线性信号,这种信号可以采用分形理论分析其特征[3-5]。因此,可以采用单重分形描述压缩机出口处动态压力特征。
根据压缩机出口处动态压力波形的频率分布,可以在分析其分形特征之前,采用时频分析的方法,将信号分解为多个频率特征相异的分量,达到分析其奇异特征的目的。常用的时频分析方法有小波变换、经验模态分解及经验小波变换等。其中,小波变换过于依赖小波函数,不具备自适应性。经验模态分解计算时间较长,效率较低。而经验小波变换(empirical wavelet transform,EWT)可以有效地弥补以上2种方法的不足,其作为一种具有完备理论且具有自适应性的方法,已被用于医学、航空及机械等领域[6-8]。因此,可采用EWT进行信号的特征分析。
以离心压缩机系统出口处气体的动态压力为分析对象,采用EWT分解将动态信号分解为多个含有不同频率特征的模态分量。进一步采用分形理论分析模态分量的奇异特征以识别系统的喘振状态。
1 相关理论
1.1 经验小波分解
经验小波变换是一种小波变换框架下的自适应变换理论。特点是将模态看作是幅度和频率的信号,以此实现模态的分解和有效信息的检索[6]。
对于一维时间序列,首先对其进行FFT分析,根据Shannon准则的要求,将频率谱归为[0, π],记为X(ω)。将Fourier频谱分为N段,则信号被连续分解为N个模态分量,定义ωn为各个模态分量的边界,如(1)式所示(ω0=0,ωN=π)。

(1)

使用传统的频带划分方法,求出X(ω)的前N个极大值及其对应的角频率,并按照角频率大小排序为Ω1,Ω2,Ω3,…,ΩN。以此将整个频谱图划分为N个区间。以ωn为中心,定义过渡带Tn=2τn,完成EWT分解,如图1所示。
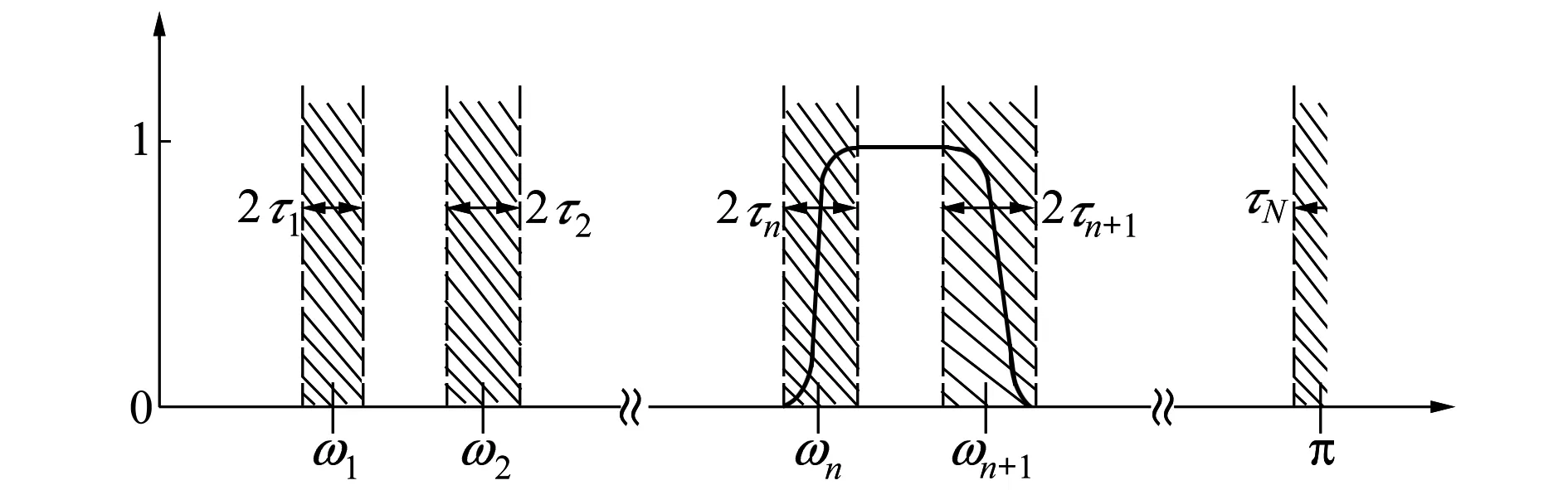
图1 EWT分解图


构造经验小波变换的细节系数Wx(n,t)和近似系数Wx(0,t)
(4)
(5)
将原始信号表示为近似值和细节值的叠加,得到经验小波变换的重构信号
(6)
进一步,将该重构信号化简为
(7)
则原始信号分解后的各个模态分量为
1.2 单重分形及其物理意义
单重分形是指时间序列中某种过程的特征从不同的空间尺度或不同的时间尺度来看都是相同的或者极为相似的。时间序列的单重分形一般通过自相关函数和Hurst参数分析。
1.2.1 自相关函数
自相关函数主要用来反映在一个过程中,不同时刻过程的相关程度随时间的变换。
对于一个随机过程xi,如果存在数学期望E(xi)和方差var(xi),则该过程称为二阶过程,其自相关函数就是k的函数,k也称时间序列的迟滞点数。如(10)式所示

(10)
1.2.2 Hurst参数及R/S算法
Hurst参数可以量化时间序列的自相关性,从而衡量其长期记忆性。通常采用R/S分析法(又称为重标极差分析法)根据时间序列按照长相关特性的幂指数规律进行计算[9]。
将时间序列xk(k=1,2,3,…,N)等分为长度为n的m个子序列Xa,子序列的元素、平均值和标准差分别记为xk,a,ea和Sa(a=1,2,3,…,m)。其中
设xk的累积偏差为Xt,N,则

(13)
定义极差R为Xt,N的最大值和最小值之差,表示该时间序列最大变化范围。

(14)
用xk的标准差去除R,进行重标,可得

(15)
对(15)式两边取对数,可得

(16)
根据(16)式,利用最小二乘法拟合R/S与n的对数曲线。则曲线的斜率为Hurst参数,简称H。其中R,S和C分别表示重新标度的极差、标准差和时间增量区间长度(样本观察值数目)。
根据统计理论,Hurst参数的取值范围为0~1,系统的正相关性随着Hurst参数的变大而变大。
对于离心压缩机出口处动态压力来说,当Hurst参数处于0~0.5时,说明该段时间内动态压力是反相关的。当Hurst参数处于0.5~1时,说明这段时间动态压力有很明显的正相关性。而当Hurst参数越接近0.5时,压缩机动态压力特性也就越不稳定,随机性也就越大。因此,Hurst参数可以分析压缩机出口处动态压力的突发特性。
1.2.3 皮尔逊相关系数
皮尔逊相关系数可以度量变量X和Y之间的相关性,定义为2个向量之间的协方差和标准差之商。
(17)
相关系数的取值位于-1和1之间。当相关系数小于0时,2个向量呈现负相关特性,并且相关系数越接近-1,负相关特性越强。当相关系数大于0时,2个向量呈现正相关特性,并且相关系数值越接近1,正相关特性越强。
2 出口动态压力采集及波形分析
2.1 数据采集
实验所采用的离心压缩机由一台800 kW的直流电动机驱动。系统工作时,自然室温状态下的空气经空气过滤器流入系统,经管路进入风室等待压缩。当压缩机工作时,气体被压缩。压缩完成后,通过控制电动防喘振阀将气体排入大气。
系统在不同工况下出口处的动态压力由动态压力采集模块采集,数据采集时间为635.5 s。本文选取其中的150~300 s共150 s数据进行分析,并且将第150 s定义为时间起点,这个过程包含系统由稳定状态到喘振的全过程。
2.2 离心压缩机出口处动态压力波形
通过逐渐关闭防喘振阀的开度,压缩机系统从稳定状态经过过渡过程进入喘振状态。图2a)为全过程的出口动态压力波形图(本文以PSI为压力计算单位,1 PSI≈6.89 kPa)。当防喘振阀完全打开时,压缩机系统处于稳定状态,波形如图2b)所示。此时出口处动态压力幅值较小,并且呈现明显的随机特性。随着防喘振阀的逐渐关闭,系统进入过渡状态,如图2c)所示。此阶段,动态压力的幅值逐渐增加,并且开始表现出一定的周期特征。随着失稳状态的加深,系统进入喘振状态,如图2d)所示。此阶段,动态压力的幅值已接近稳态时的3倍,并且表现出明显的周期振动。

图2 离心压缩机出口动态压力波形(压力计算单位为PSI)
3 出口处动态压力波形的重构
在分析压缩机出口处动态压力的单重分形特征之前,对其进行EWT分解。进一步根据相关系数对分解后的模态分量进行重构。
采用EWT变换将出口处动态压力的3个阶段,稳态(10~12 s),过渡过程(110~112 s)和喘振(130~132 s)的波形分解为5层模态分量(IMF1-IMF5),如图3所示。

图3 出口处动态压力的EWT分解结果及重构信号
由图3a)可知,在全过程的5个模态分量中,IMF1在系统不同工况下未表现出明显的差异,无法对系统的工作状态进行识别。IMF2和IMF3在系统进入喘振状态时幅值均发生突变,可以有效地区分稳态和喘振。但是过渡过程阶段表现不十分明显。进一步,相对于IMF3的波形,IMF2的波形幅值变化更为剧烈。IMF4和IMF5从幅值上均可以识别出系统的过渡过程,但是其稳定状态和喘振幅值差异较小。相对于IMF4的波形,IMF5的波形中包含更多的高频随机特征。
由图3b)~3d)可知,在稳态,过渡过程和喘振状态时,IMF1、IMF2和IMF3的波形可以反映出系统的低频特征,而IMF4和IMF5的波形可以描述系统的高频特征。其中,从IMF2的波形中可以明显看出系统由稳态经过过渡过程至喘振时的周期性逐渐变强。而IMF5的波形中包含有较多的系统随机特性。
进一步,为了避免特征信号的丢失,采用皮尔逊相关系数分析各模态分量与原始信号的相关性,如表1所示。由相关系数可知,在低频信号中,IMF2与原始信号相关程度最高。而在高频信号中,IMF5与原始信号相关程度较高。根据图3及表1的分析结果,可选择低频信号中(IMF1-IMF3)与原始信号相关性较高的模态分量与高频信号中(IMF4-IMF5)与原始信号相关性较高的模态分量进行重构。因此,选取IMF2与IMF5进行重构,重构信号如图3所示。

表1 各模态分量与原始信号的相关性
由图3可知,重构信号既可以区分系统的稳态和喘振,又可以反映系统的过渡过程,并滤除掉影响系统特征分析的信号。因此,相对于原始信号,采用重构信号更容易识别系统的工作状态。
4 出口处动态压力波形的单重分形
4.1 自相关函数
分别选取压缩机在不同状态下2 s的信号做出其自相关函数,如图4所示,此时迟滞点数k最大值为40 960。
图4a)表示在稳态时,重构信号的自相关函数变化范围集中在-0.1~0.1之间,波动范围不大,并且随着迟滞点数k的增加,先有一个明显的减少,随后在r(k)=0处随机振动。整个过程中自相关函数的变化趋势没有明显的周期特征,波形的自相关性不强,表现出较强的随机性。
图4b)表示在过渡过程时,重构信号的自相关函数变化范围同样集中在-0.1~0.1之间。与稳态相比较,过渡过程波形的自相关函数波动较大,但仍没有明显的周期性。
图4c)表示在喘振时,重构信号的自相关函数变化范围处于±1之间,呈现出周期性衰减趋势。相比于稳态和过渡状态,自相关函数波动较大。
由上述分析可知,当k=40 960时,随着系统由稳定状态进入喘振,重构信号的自相关函数由随机性逐渐呈现出有规律的周期性。并且随着迟滞点数的增加,自相关函数逐渐趋于0。此时可以明显地识别出系统的稳态和喘振,而稳态和过渡过程从波形特征和数值上不易识别。
为进一步分析重构信号的自相关函数特征,选取k最大值为50进行分析。此时,分别在不同工作状态下选取4个时段,每个时段为2 s,以其为分析单元,做出自相关函数,如图5所示。

图4 不同状态下的自相关函数(k=40 960)

图5 不同状态下的自相关函数(k=50)
由图5可知,当系统处于稳定状态时,其自相关函数迅速衰减至0~0.2之间,随后保持平稳。在过渡过程中,自相关函数衰减的程度低于稳态,衰减至0.2~0.8之间,随着系统逐渐接近喘振,其自相关函数衰减程度逐渐降低。当系统处于喘振状态时,自相关函数仅衰减至0.85左右,随后保持平稳。此时系统的3种状态特征差异性较大,易于识别。
4.2 Hurst参数
以2 s为分析单元,重构信号和原始信号的Hurst参数变化曲线如图6所示。

图6 Hurst参数对比
可以看出,Hurst参数始终都在0.5~1之间,说明离心压缩机出口处动态压力始终具有正相关特性,且喘振时波形的相关特性远高于稳定状态。
在稳态时,原始信号的Hurst参数变化范围为0.62~0.73,而重构信号的变化范围为0.62~0.68。相比于重构信号,原始信号状态判断误判的可能性较大。在过渡过程中,2种信号均发生了突变,原始信号的Hurst参数突变至0.94左右,重构信号增加至0.85左右。由于重构信号剔除掉了与原始信号相关性较低的模态分量,因此重构信号整体波形更加稳定,峰值低于原始信号。随着过渡过程的深入,进入喘振时,原始信号的Hurst参数有一个较大幅度的衰减,至0.85左右,随后基本保持稳定。这种非平稳的震荡不利于压缩机状态特征的识别,易造成误判。而重构信号的Hurst参数基本稳定于0.85左右,其稳定性高于原始信号。因此,在这种状态的识别上,采用重构信号判断系统工作状态准确率高于原始信号。
5 结 论
以800 kW的离心压缩机系统出口处气体的动态压力为分析对象,采用经验小波变换和相关系数重构原始信号,并通过分析其自相关函数和Hurst参数研究其单重分形特征。
研究结果表明,离心压缩机出口动态压力的重构信号的自相关函数与系统的工作状态存在关联关系。当迟滞点数为40 960时,可以通过自相关函数波形特征识别系统的工作状态。而当迟滞点数为50时,可以通过自相关函数数值识别系统的工作状态。进一步,相对于原始信号,采用重构信号的Hurst参数更易识别出离心压缩机系统的喘振状态。因此,结合EWT和单重分形研究,可以降低离心压缩机喘振识别误判率。同时,经过实验测试,采用该方法可以快速地实时跟踪系统的工作状态,完成在线监测。这对后期实现压缩机健康工作状态的远程监控奠定了技术基础。
