一种基于智能控制算法的芯片烘箱PID温度控制器

梁达平，王鸿斌，赵利民

(1.天水师范学院电信与电气工程学院，甘肃 天水 741000；2.天水华天科技股份有限公司，甘肃 天水 741000)

洁净无氧化芯片烘箱是集成电路封装生产线上的重要生产设备，其功能结构如图1所示[1]。为了达到芯片封装的工艺要求，需要该设备具备较高的温控性能（包括快速加温降温能力、在高温175℃状态下的恒温能力、以及温度均匀性等）。但是，由于烘箱在高温固化时腔体内会放置较多的烘烤产品托盘及料盒，从而导致排风道空气流向复杂多变、难以预测，其温度环境模型呈现出大惯性时滞非线性系统特征，这就给烘箱的温度控制算法设计带来了很大困难。

图1 芯片烘箱结构图

显然，如何去除温控系统中时滞环节对控制性能带来的负面影响是解决控制瓶颈问题的关键。为此，我们选用控制算法中常用的Smith预估器来消除时滞效应，因为Smith预估器可以通过加入预估反馈环节补偿系统滞后带来的PID校正装置快速性不足问题。但是，成功的Smith预估器应用取决于是否能够建立精确的被控系统模型，这一点对于芯片烘箱来说是较困难的。目前，工程界主要从传统理论中的有模型算法、相关交叉学科中的无模型算法、以及智能控制算法等角度来探讨解决方案和思路[2]。

例如，文献[3]在传统的Smith预估控制结构中，通过以李雅普诺夫稳定性理论构建自适应控制模型的方法作为Smith预估器中的非时滞环节传递函数模型，取得了一种便于工程化应用的实施方案，有较高的实用价值。但该自适应模型对于模型易变、缺乏经验性认识的时滞系统来说，并未解决模型精确性问题。文献[4]将Smith预估器与滑模控制相结合优化了粮食恒温烘干装置的综合性能，用Smith预估抑制烘干塔的大滞后问题，用滑模控制解决了非线性时变因素，提高了外部抗干扰性能，增强了系统的鲁棒性。整个控制结构中关于如何获得Smith补偿模型较精确的估计并未提出可行方案。文献[5]在常规Smith预估器结构中引入了2个负反馈，使系统闭环传递函数的特征方程中去除了预估参考模型带来的影响，从一定程序上减弱了由于预估器不精确对控制的劣化作用，但对于不同控制领域问题的泛化性解决能力有待验证。文献[6]首先全面分析了解决温度控制大时滞问题可以采用有模型法和无模型法，但各有缺点。讨论了Smith预估模型的主要参数失真对控制劣化带来的影响，将影响最大的参数采用在线系统辨识方法进行分段校正，取得了较好的温控效果，一定程序上解决了Smith预估模型精度问题。文献[7]将Smith预估器加入到PID控制结构中，并将PID控制的调节作用通过模糊控制规则来实现，从一定程序上改善了系统的时滞性和快速性，但仍未解决预估器模型精确度不够带来的补偿过失风险问题。[3-7]

基于上述研究思路及成果，本文提出将机器学习神经网络算法引入到基于Smith预估器的温度控制器结构中，利用改进的Smith预估器与多层反向传播神经网络（以下简称BP神经网络）及PID控制器相连，来优化整体控制性能。改进型Smith预估PID控制器的结构主要分为两部分。其中一部分是将神经网络与PID控制器相结合，采用在线学习的BP神经网络1自适应地调整PID参数，以提高控制器的动态性能；另一部分是将神经网络与Smith预估器相结合，使用BP神经网络2来识别受控对象的非线性模型，以提高其建模精度，从而使Smith预估器可以很好地补偿纯时间延迟。BP神经网络、PID控制器和Smith预估器的集成提高了温度控制系统的鲁棒性和快速性。

1 传统Smith预估器模型描述

传统的Smith预估器工作原理就是在PID控制器之后接入补偿环节，对被控制对象去除时滞环节后的数学模型进行模拟，如图2所示。

图2 Smith预估器原理[8]

图2中，Smith预估器补偿环节的传递函数Gm(s)表示为计算式(1)：

Gp0(s)·e-τs在考虑时间延迟的受控对象的开环传递函数，如果未添加Smith预估器，则系统的闭环传递函数如计算式(2)所示：

式(2)中，Gc(s)是PID控制器的传递函数。

添加Smith预估器后，在理想状态下Gm0=Gp0，则系统的闭环传递函数将变化如计算式(3)所示：

由式(3)可知，在理想状态下可以将被控制对象的时滞环节e-τs分离出来，使系统的反馈通道在时滞环节之前引回。显然，此时未被滞后的反馈信号可以极大地改善系统的响应速度。但是，计算式(1)、(2)、(3)的计算只是基于纯理论精确补偿模型得到的，Smith预估补偿算法最大的不足在于如果被控制对象模型无法被精确建立，则补偿效果会大大降低，甚至起负面作用。

2 改进型控制器设计

本文提出的改进型PID控制器结构如图3所示，该结构充分借鉴了相关行业的工业控制算法经验，有针对性地解决了芯片烘箱温控系统中非线性、大时滞、高复杂度所带来的精度干扰问题，具有明显的行业先进性和可操作性。控制器分为两部分，一部分是PID控制器及BP神经网络1（图3中表示为BPNN1），BP神经网络1可以实现PID控制器参数的自整定，提高PID控制效率；另一部分是Smith预估器及BP神经网络2（图3中表示为BPNN2），其中Smith预估器用于减少温控系统中时滞环节的影响，BP神经网络2用于识别受控对象G0(s)的开环模型，神经网络算法具备更高的系统辩识精度可以使Smith预估器更有效地补偿时延效应。

图3 改进型控制器结构图

2.1 PID控制器与BP神经网络1

神经网络算法具备很强的拟合与自适应能力，可在系统辨识、参数优化、状态拟合等方面与其它控制方法很好地结合。因此，在PID控制算法的基础上，通过在线学习型BP神经网络自整定PID环节的系数，提高了PID控制的执行效率。

应用神经网络算法的PID控制器由两部分组成：PID控制器和BP神经网络1。其中，PID控制器在前向通道中控制受控对象；BP神经网络1则根据当前时刻的设定值、输出值、误差值实时调整PID控制器中3个环节的放大系数KP、KI、KD。其结构如图4所示。

图4 BP神经网络1结构示意图

BP神经网络1的输入信号是[r(k)，e(k)，c(k)]T，输出信号是[Kp，KI，KD]T。

其中k是离散时间序列（k=1，2，3...）；r(k)是在时间k的设定温度；e(k)是时间k的误差值；c(k)是在时间k的实际输出测量温度；KP，KI，KD分别表示PID控制器的比例、积分和微分系数。

由于PID参数不能为负，因此将输出层的激活函数选定为Sigmoid函数，隐藏层的激活函数也选用Sigmoid函数。根据神经网络的常规计算规则[9]，可以确定神经网络的起始参数包括：机器学习方式采用在线学习，学习率η=0.3，权值更新系数α=0.1，隐藏层神经元数量为3，各节点初始权重采用(-0.05，0.05)的随机值。

增量式PID控制算法用于计算控制输出电压Uc(k)，如计算式(4)所示：

误差值e(k)的计算方法表示为计算式(5)：

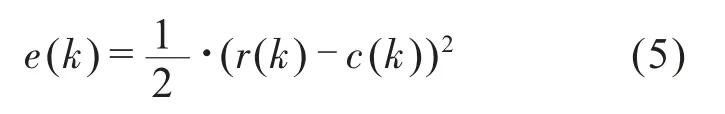
利用梯度下降法，依次更新网络输出层和隐藏层的权值。各神经元的权值调整方法如计算式(6)所示：

式(6)中，Δω(k)是权值调整值；η是学习速率。

基于BP神经网络的PID控制算法执行步骤如表1所示。

表1 BP神经网络1数据集训练流程

2.2 Smith预估器与BP神经网络2

计算式(2)与(3)比较可以看出，Smith预估器是通过反馈补偿的方式来分离时滞环节e-τs和Go(s)，这等效于将受控对象的时滞环节置于控制闭环之外。

由于Smith预估器的补偿效果取决于辨识受控系统模型的准确程度，因此采用图5所示的BP神经网络来拟合系统，以提高建模精度。

图5 BP神经网络2结构示意图

受控对象是单输入单输出非线性系统，其描述如计算式(7)所示：

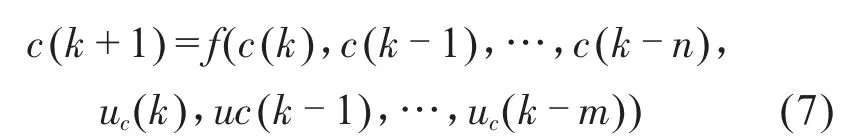
式(7)中Uc(k)和c(k)分别是对象在时刻k的输入和输出；m和n分别表示开始计算及采集Uc(k)、c(k)信号的起始时刻；c(k+1)为非线性函数。

神经网络2的输入信号是Uc(t)(k-m≤t≤k)和c(t)(k-n≤t≤k)，输出信号是c(k+1)。其起始参数包括：机器学习方式采用在线学习，学习率η=0.3，权值更新系数α=0.1，隐藏层神经元数量为5，各节点初始权重采用(-0.05，0.05)的随机值，采样保留阶数m=4，n=4。

BP神经网络2的主要训练步骤如表2所示。

表2 BP神经网络2数据集训练流程

3 在线BP神经网络的训练样例获取

从上述可知，BP神经网络1采用的是在线方式，由于设备温控系统可以持续不断的保存设定温度值及实时温度值，这些历史生产数据通过计算误差值、误差变化率、权值调整值等指标对控制器中的PID参数进行分类评价，形成不断增长的训练数据集，根据BP神经网络的反向传播进行自动化机器学习，达到不断优化网络神经元权重值的目的。

程序运行流程分为两个阶段，在安装执行的初期，由于历史数据较少故而首先采用传统的PID控制算法（也可以配合基本的专家控制、模糊控制规则辅助框定PID参数的范围），当数据量达到一定的阈值时，程序自动切换为BP神经网络与PID结合控制的模式。具体的执行流程如表3所示。

表3 BP神经网络1计算模式切换的执行流程

BP神经网络2的功能是逼近烘箱设备被控对象的精确数据模型，需要根据预估值与实测温度值，采用与BP神经网络1类似的评价方式标记不断增长的训练数据集，以及完成网络神经节点的权重值进化。其计算模式切换的执行流程与表3类似。

4 结果与讨论

在本节中，通过仿真和实体设备实验验证了所提出的BP神经网络-Smith预估-PID控制算法的性能。首先，根据第3节中推导的数学模型，在MatLab软件的Simulink平台中构建系统的仿真框图。测试并比较了采用3种算法的控制器（传统PID算法，传统Smith预估算法、神经网络-Smith预估-PID算法）；然后，在选定的实体烘箱设备中收集了阶跃输入下温度响应曲线；最后，根据仿真和实验结果进行了全面的讨论。

4.1 仿真结果

4.1.1 被控制对象的数学模型

根据相关文献的研究和分析表明[10]，对于具有自平衡能力的大惯性时滞系统，可通过一阶或二阶惯性环节与时滞环节的乘积来描述其传递函数。芯片烘箱腔体内部的温度控制环境具有封闭性和自稳定性，属于典型的自平衡系统，采用一阶惯性及时滞环节加以描述，如计算式(8)所示：

式(8)中，KC为放大系数，TC为一阶惯性环节的时间常数，τ为时滞环节的时间常数。

采用反应曲线参数整定法[11]，在系统中引入阶跃输入信号，测量系统开环状态的输出响应曲线，于曲线变化最快处作切线，切点为P点，与时间轴交于τ点，交温度稳态值的渐近线于TC点，如此操作确定传递函数的参数KC、TC、τ。如图6所示，使用MatLab对烘烤数据进行曲线拟合[12]，绘制出系统反应曲线，计算出参数值分别为TC=660，τ=155，KC=1.2。

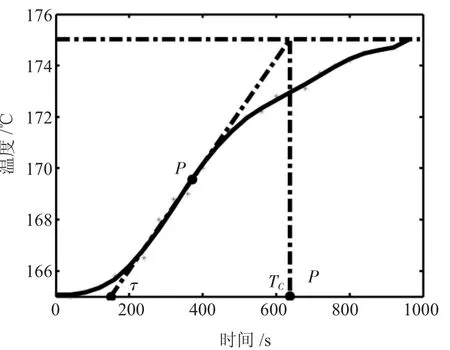
图6 芯片烘箱温控曲线图[13]

根据图3所示的控制系统方框图在Simulink平台中构建仿真模型。其中，神经网络模型使用MatLab中Sigmoid函数命令tansig来实现，然后利用神经网络工具箱函数feedforwardnet、configure、train对神经网络进行培训和固化，以生成函数模块。其它环节采用Simulink常规传递函数模块实现。分别引入振幅为175℃的阶跃信号和振幅为175℃且频率为0.002 5 Hz的正弦信号作为系统输入，比较传统PID、传统Smith预估、改进型Smith预估三种算法控制器的响应曲线性能。

4.1.2 阶跃响应

在仿真系统中输入幅度为175℃阶跃信号时，系统的响应曲线如图7所示。

图7 仿真控制器阶跃响应比较

首先，由于3种算法均含有PID控制的积分功能，所以响应曲线最终都可进入稳态阶段，使输出响应达到目标值，但是上升阶段和调节阶段的性能表现存在差异。在上升阶段，改进型Smith预估控制器响应速度最快，基本上可以达到无滞后启动。传统Smith预估和传统PID的动作时间大体相同，约需要8 s开始动作。在调节阶段，传统PID控制器产生的最大超调为1%，而传统Smith预估和改进型Smith预估的最大超调量分别为0.15%和0.05%。

相比于另外2种算法控制器，改进型Smith预估算法分别在预估器和PID控制器中加入了神经网络，一方面提高了预估器对被控制对象数学模型的实时拟合的精确度，消除了因预估模型差异带来的滞后补偿失效问题，充分发挥出Smith预估的作用，从而显著提升了系统的响应速度；另一方面，利用PID控制器中神经网络的实时调节能力，改善了PID参数自整定效率和准确度，更好地发挥出PID控制的校正功能。总之，所加入的2个神经网络从滞后补偿与PID控制2个主要矛盾层面大幅提高了系统的鲁棒性。

4.1.2 正弦轨迹

仿真系统引入振幅为175℃，频率为0.002 5 Hz的正弦输入信号，系统对应的3种控制器响应曲线如图8所示。

图8 仿真控制器正弦响应比较

图8与图7中的阶跃响应曲线相比，由于目标设定值变为时变信号，虽然3种控制器均可跟踪设定曲线，但是会显示出不同程度的明显滞后。跟踪精度排序依次为改进型Smith预估控制器、传统Smith预估、传统PID。其中，改进型Smith预估的最大误差为0.83℃，平均误差为0.51℃。传统PID控制的最大跟踪误差为1.72℃，平均误差为1.59℃。传统Smith预估的最大误差为1.25℃，平均误差为0.91℃。由此可见，改进型Smith预估控制器在这3种控制器中具有最佳的动态性能。

4.2 实验验证

芯片烘箱主机上的控制和数据采集程序是通过Visual Basic进行编程的，如图9所示。在该系统中改进型Smith预估控制算法单元由Visual C++开发完成后以DLL动态链接库调用的方式加载到主控制程序中。为了减小因设备腔体形状及降温通道路径差异对数据分析带来的影响，在整个实验过程中选择同一台烘箱设备、并选择采用相同工艺规范加工的芯片批次。

图9 实际温控固化曲线图

4.2.1 阶跃响应

当烘箱设备设定输入幅度为175℃的阶跃信号时，其输出温度的响应曲线如图10所示。

图10 实际控制器阶跃响应比较

从图10中可以看出，实际系统测试结果与仿真结果呈现出来的主要特征及性能排名先后是一致的。在温度上升阶段，改进型Smith预估控制器的上升时间约为1 s，传统Smith预估和传统PID的上升时间大体相同，约为8～10 s。在调节阶段，改进型Smith预估，传统Smith预估和传统PID的调整时间分别为12 min、17 min和21 min。3种控制器均出现不同程度的超调，其中改进型Smith预估控制的超调量仅为0.5%，而传统Smith预估和传统PID的超调量分别为0.7%和1.7%。在稳态阶段，3种控制器的稳态误差均存在，但数值并不大，都可控制在±0.1℃范围内。

通过与4.1节进行比较可以发现，由于实际系统在测试中存在不可控的非线性因素影响，性能水平比仿真系统要略低。但是其最终结论是一致的，并且改进型Smith预估控制更优的系统控制性能改善作用是很明显的。响应曲线在各个阶段的形态均表现出，改进算法可以在维持稳定性的同时更快地提高响应速度，去滞后效果也十分明显。

5 结 论

针对芯片烘箱设备温控环境的非线性和时滞问题，本文提出了一种结合BP神经网络和Smith预估器的改进型PID控制方法。将BP神经网络分别用于PID控制器的参数自整定及Smith预估器对被控制对象模型的拟合，增加了非线性温控系统的鲁棒性，并且使Smith预估器更为精确地补偿了温控大惯性时间延迟，提高了设备的调节速度。仿真和实测结果均表明，改进型Smith预估控制算法的各方面性能明显优于传统PID控制器及传统Smith预估器，可广泛应用于各类嵌入式工业控制设备的PID自整定控制系统中，具备较高的推广价值。