基于粗糙集理论和SVM的雷达辐射源信号快速识别算法研究

杨素敏 崔静 赵德勇 刘启明

（陆军工程大学石家庄校区 河北省石家庄市 050003）

在信息战中，快速、准确分类识别出雷达辐射源信号对电子情报侦察起决定作用。文献在分析雷达识别信号特征的基础上，提出了基于SVM（Support Vector Machine）和深度学习的雷达辐射源识别方法。文献利用特征降维和一类分类器设计和参数优化实现雷达目标自动识别；文献对辐射源的多域特征进行提取，并通过多核学习的方式实现对辐射源的识别，这些算法都显著提升了雷达辐射源的识别效能。但雷达辐射源信号指标众多，如到达时间（TOA, Time of Arrival）、载波频率（RF, Radio Frequency）、脉冲宽度（PW, Pulse Width）、脉冲幅度（PA, Pulse Amplitude）、达到方向（DOA, Direction of Arrival）、脉冲重复周期(PRI,Pulse Repetition Interval)、工作带宽、带内功率平坦度、脉冲包络、信号频谱等，如果不精简指标，样本数据量大必然影响SVM 识别速度。

本文提出了基于粗糙集理论和SVM 的雷达辐射源信号快速识别算法，首先利用粗糙集理论在数据挖掘方面的优势，通过样本数据本身计算出各指标的客观权重，约简出影响分类识别的关键指标；其次优化SVM 中的cost 和gamma 参数，以及采用不同核函数的方式对所有指标和约简指标分别进行识别。仿真实验表明，选取合适cost 和gamma 参数以及核函数，约简指标也能使分类识别准确率达到或接近100%，这对提高雷达辐射源信号的分类识别实时性有重大作用。

1 相关理论

1.1 粗糙集理论

粗糙集理论仅通过决策表中的原始数据挖掘出隐含的知识，直接获取规则，并利用粗糙集理论约简方法有效地去除冗余指标，有利于客观评价数据样本的效能。

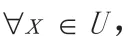
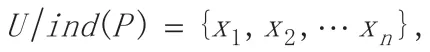
知识P 相对于Q 的条件熵H(Q|P)为：

知识P 相对于Q 的互信息I(P;Q)为：

（3）指标权重定义：指标的重要性通过指标权重评价，指标权重包括客观权重和主观权重。客观权重SGFo 利用互信息的增量与指标本身的信息熵的比值计算，公式如下：

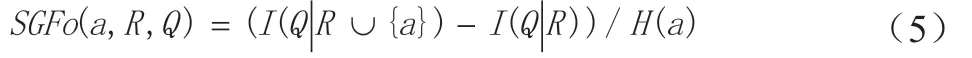
主观权重SGFs 通过本领域专家根据自己的经验确定，指标总权重SGFtotal 为：

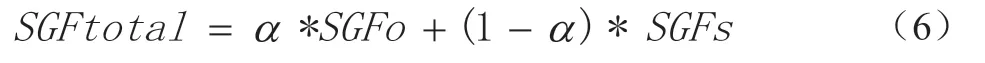
其中α 是客观权重系数。

1.2 SVM理论

随着核函数理论的引入，SVM 通过非线性映射函数把输入样本数据从低维空间映射到高维空间，非线性分类问题得到解决。

SVM 分类运算中涉及的参数很多，对分类效果影响最大的参数是g(gamma)、c(cost)和核函数。常见的核函数类型有线性核函数、多项式函数和RBF 高斯核函数。g 参数用于设置多项式和RBF 核函数的gamma 值，c 参数用于设置损失函数。在SVM 分类过程动态调整g 和c 两个参数可以使分类准确率达到最佳。

2 粗糙集和SVM的分类识别算法

本文所提算法主要包含2 个步骤，一是利用粗糙集理论进行指标的约简；二是利用SVM 对所得的约简指标和全部指标进行分类识别，下面详细描述算法的实现过程。

2.1 指标约简

对于类似于S={U,A,V,f}的决策系统，目的是在保证决策结果不变的情况，尽可能地约简条件属性C 中的个数。具体步骤如下：

（1）计算条件指标集C 与决策集D 的总互信息值I(C;D)；

（2）利用公式（6）计算所有指标的权重，选取值最大的加入集合C，并进行如下操作：

对于剩余的每个指标c∈C，利用公式（5）计算客观权重，与主观权重通过一定的比例参数相加得出综合权重，从运算结果中选出综合权重最大的元素c，如果多个指标的综合权重相同，则比较它们的互信息值，并把对应最大互信息值的指标加入到指标约简集C；

②判断所得约简指标集的互信息值是否与I(C;D)相同，两者如果相同，则转到（3），否则转到①；

（3）C即为决策表的一个约简集。

2.2 SVM分类识别算法

基于雷达辐射源信号的样本数据在原始特征空间中可分性比较差，多项式核函数和RBF 核函数都能将原始输入样本映射到了高维空间，识别效果显著提高。本文分别对约简指标和全部指标进行SVM 分类识别，训练数据分为无噪声和添加5 分贝、10 分贝、15 分贝和20 分贝白噪声干扰两类，采用多项式和RBF 两种核函数，识别过程中不断优化c与g 参数以达到最优解。算法描述如下：

3 实例分析

读取约简指标样本数据;

设置训练样本和测试样本;

3.1 仿真雷达信号生成

本文利用仿真软件产生6 类39 部雷达辐射源信号，分别为常规雷达信号、频率捷变信号、FSK 信号、LFM 信号、BPSK 信号、QPSK 信号。如表1 所示。信号评价指标选取信号DOA、RF、PW、PRI 和极化特性5 个指标。设定雷达辐射源信号RF 参数在中心频率±10MHz 内随机取值，PW为中心值±10%内随机取值，SNR 统一设定为5dB。模拟生成500 组信号。其中300 组信号作为训练集，用于生成分类模型，其余200 组数据用于生成测试集，实现对模型的验证与测试。本文中RF 信号的主要以正弦范围的中心点上下震荡10%左右。

表1 ：雷达辐射源识别信号

为了便于图示，PW 利用其倒数PRF（Pulse Repetition Frequency）进行代替，PRF 的频率值在172 左右，PRF 采用正弦调制产生信号，通常振幅值为其平均值的5%左右。

PRI 是在600-630 之间以高斯正态分布进行抖动模拟生成的信号。

3.2 粗糙集指标约简

（1）按照2.1 节指标约简过程，先计算表1 条件指标集C 相对于决策集D 的互信息，结果如下：

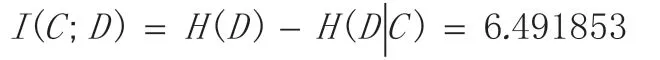
（2）按照定义2 和定义3 中的互信息和指标权重公式，分别计算5 个指标的相关数据，如表2 所示：

表2 ：指标的信息熵、互信息、重要度和总权重

从表1 中可以看出，指标5 的重要性最大，因此选择指标5 为第一个重要指标，加入C={c}，接着将指标c与剩余其他4 个指标组合，再次计算互信息和指标重要性，结果如表3 所示。从表3 中可以看出，指标2 和指标5 组合的重要性最大，因此选择指标2 为第二个重要指标加入C={c,c}，继续重复以上步骤，得到C与剩余指标的组合与运算，结果如表4 所示。从表4 中可以看出，指标2、指标3 和指标5 组合的重要性最大，因此选择指标3 为第三个重要属性并加入C={c,c,c}，此时3 个元素的互信息和总的互信息相等，至此约简结束。

表3 ：指标的信息熵、互信息、重要度和总权重

表4 ：属性的信息熵、互信息、属性重要度和权重

3.3 SVM分类识别

为了验证约简指标的分类准确率，针对表1 中的数据，分别采用多项式核函数和RBF 核函数进行了DOA、RF、PRF、PRI 和极化特性全部5 个指标以及RF、PW 和极化特性3 个约简指标的仿真实验。训练集采用无噪声和不同分贝白噪声干扰两种类型。

图1 和图2 所示的是在无噪声干扰下，3 个约简指标和5 个全部指标利用RBF 核函数和多项式核函数进行的SVM分类实验结果。从分类结果中可以看出，在SVM 优化模式下，无论是3 个约简指标还是5 个全部指标，利用多项式核函数和RBF 核函数的分类准确率都能达到100%。图3 和图4 所示的是在RF 信号中依次加入5dB、10dB、15dB、20dB白噪声信号，利用RBF 核函数进行SVM 分类的实验结果。从仿真实验结果看，3 约简指标除了在15db 下分类准确类为84.4444%之外，其余情况下3 约简指标和5 全部指标的分类准确率都能达到100%，证明指标约简后对分类识别效果影响较小。但由于3 约简指标的样本数据较少，能提升分类识别的实时性。

图1 ：RBF 核函数SVM 分类结果

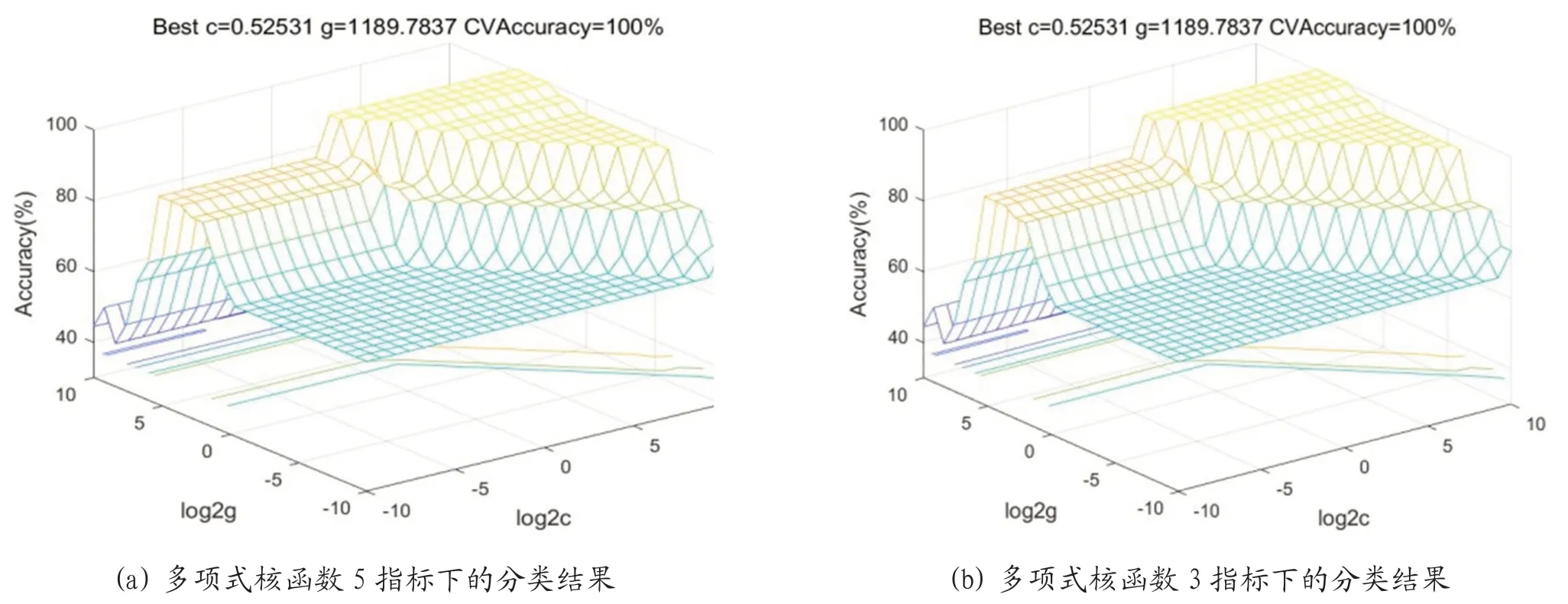
图2 ：多项式核函数下SVM 分类结果

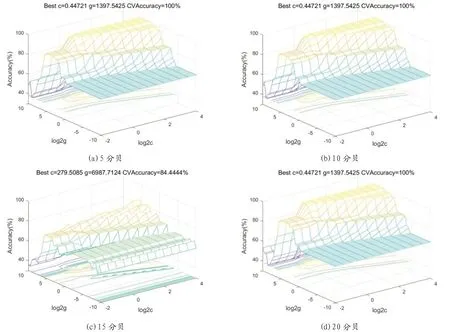
图3 ：RBF 核函数在不同分贝白噪声干扰下3 指标SVM 分类结果

图4 ：RBF 核函数不同分贝白噪声干扰下5 指标SVM 分类结果

4 结论

雷达辐射源信号识别的准确、快速对信息战起着关键性的作用，本文首先以粗糙集理论挖掘出各指标的客观权重，并结合专家的经验知识，从众多指标中优选出关键指标。其次，在有、无白噪声干扰两类样本数据下，利用多项式核函数和RBF 核函数下分别进行了5 指标和约简3 指标的SVM分类识别仿真。从实验结果看，对于无噪声干扰下的约简指标，在优化g 参数和c 参数下，多项式核函数和RBF 核函数下的SVM 识别分类准确率都能达到100%。但在白噪声干扰下偶有分类识别准确率较低的情况，在以后研究中需进一步完善算法。