基于改进三维A*算法的三栖机器人路径规划研究

李辰豪 吴启来 郭晟男

（南京理工大学 江苏省南京市 210094）

1 引言

目前，国内外研究人员针对地面机器人的研究已经取得了较大的成果，其发展也日益成熟。除此之外，在空中无人机和水中无人舰艇的开发与应用方面，很多学者都开展了较为丰富的研究。但是上述的机器人都局限于某一种特定工作环境，如，地面、空中、水面，因而针对这些机器人的研究也具有单一性。在现实世界中存在着多种环境域，当任务涉及到多种环境域时，这就要求机器人同时具备在多种环境域下的工作能力。路径规划是移动机器人运动与仿真领域的热点研究问题，国内外很多学者都在这个研究方向上进行了大量的研究与探索，但路径规划的算法仍有不足与可改进之处。

传统A*算法以路径最短作为规划目标，以此目标规划的路径并不适用一些特定目标的任务。文献中提到了机器人陆空两栖的决策切换和规划，文献提出了水陆两栖的路径规划，均不能解决水陆空三栖环境下的机器人规划问题。

在此启发下，我们提出一种适合水陆空三栖环境的基于改进三维A*算法的全局规划算法，该算法以机器人的耗能和时间的综合代价作为规划目标。

2 基于状态切换和代价分析的改进三维A*算法

2.1 传统A*算法

A*算法是一种在全局静态地图中对最短路径进行求解和规划的最有效的直接搜索方法，也是解决许多其他问题时常用的启发式算法，有着较好的性能和准确度。公式表示为：

传统的A*算法没有将机器人运动时不同运动状态之间相互切换的耗能代价以及在不同环境运动的时间、耗能代价考虑进去。只把所求解的路径长度作为规划目标，然而，在实际中，多栖机器人的路径规划、运动要考虑诸如耗能、时间等因素，以达到任务对机器人运动的时间和耗能要求。而本文提出的改进算法将对这一问题进行优化解决。

2.2 搜索邻域简介

在二维环境下，A*算法只需拓展当前节点的8个子节点，而三维环境下，需拓展26个子节点。

2.3 三栖机器人状态切换的代价分析

三栖机器人的水、陆、空自主切换控制状态机的实现如图1所示。

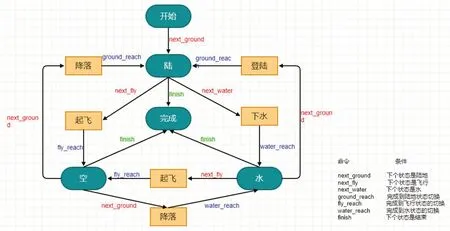
图1：机器人自主切换控制状态机

由于机器人在水陆空各个环境下的状态不相同，这使得机器人在环境变化时进行的状态切换会产生比较多的能量损耗。表1是机器人不同状态切换的能量损耗程度对应表，其对应的F切换损耗属性评价分别为{0,1,2,3,4,5}。

表1：状态切换能量损耗评价表

从当前工作状态到待选节点工作状态切换时会产生状态切换能耗，在待选工作状态向目标点的工作状态转换时也会产生状态切换能耗。

2.4 多目标启发式函数设计

当三栖机器人在现实环境下运动时，运动的能量消耗不可忽视。因此在路径规划时需要把机器人在不同环境下运动的耗能分析和运动时间都作为优化目标考虑进去。本文选择将运动耗能分析和运动时间同时作为三栖机器人最优路径规划的优化目标。又由于三栖机器人在不同环境下的运动耗能和运动时间不完全独立，彼此之间有一定的依赖关系，所以使用为每个优化目标赋予一定权值的方式对于路径规划算法的多目标启发式函数进行描述。运动过程的耗能代价分为地面运动代价、空中飞行代价以及水面运动代价。

由于运动耗能和运动时间这两个优化目标的量纲不同，很难进行统一的计算与比较，因此本文对不同环境下运动耗能代价进行统一量纲处理。以地面运动耗能代价e作为基准（保证统一量纲处理后的计算比较耗能代价的值大于等于1），采用各环境下的运动耗能代价与e的比值作为各环境下的计算比较耗能代价。

式中E、E、E分别表示地面运动、空中飞行与水面运动的统一量纲处理后的计算比较耗能代价，e、e、e表示各环境下实际的单位距离耗能代价。

在地图的三维栅格中，根据栅格存储的环境属性不同（水、陆、空），规划出一条路径之后，即可获得在地面运动的距离s、在空中飞行的距离s以及在水面运动的距离s，分别除以三栖机器人在地面运动的速度v、在空中飞行的距离v以及在水面运动的速度v。便可得到不同环境下的运动时间t、t、t。同理，对其按照空中运动的时间t进行统一量纲处理，得到计算比较运动时间T、T、T。

本文为了与原A*算法的代价函数相区分，将代价函数设为g'(n)，节点q的代价函数值g'(b)为其父节点q的代价函数值g'(a)与q到q的运动代价、状态切换对应的代价之和，因此可以得到节点q的代价函数值g'(b)表达式如下：

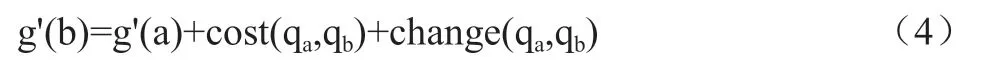
cost(q,q)表示从节点q到节点q所需要耗费代价，结合2.4的分析，cost(q,q)值的计算表达式如下：

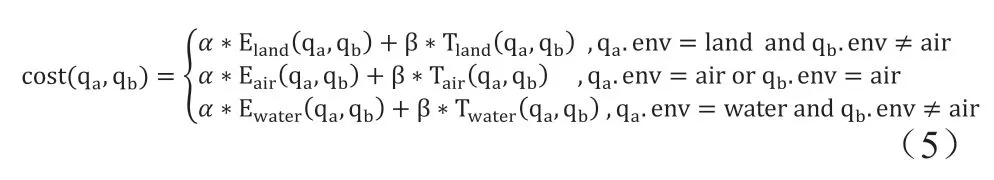
其中α与β分别为不同环境下运动过程耗能和运动时间的加权系数，且满足α+β=1，q.env，q.env分别表示节点q,q的环境属性（land、air、water）。

change(q,q)表示从节点q到节点q状态切换的代价，对其也按照地面运动的耗能进行统一量纲处理，结合表1，可得出change(q,q)值的计算表达式如下：

其中κ为正常数，F表示节点q到节点q切换损耗属性评价值。

本文为了与原A*算法的估价函数相区分，将代价设为h'(b)。h'(b)作为q至终点q的预估代价，结合前文，本文将h'(b)取为和g'(b)相同的形式，可以得到改进后的h'(b)表达式如下：

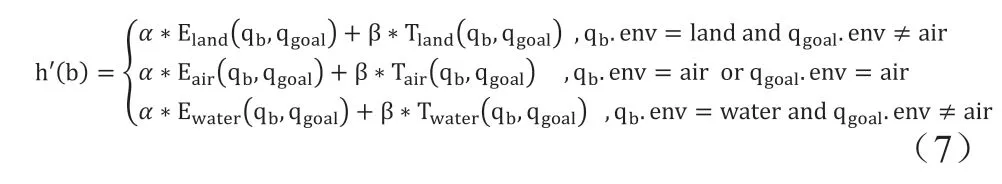
因此优化后的三维A*算法的代价函数计算公式为：

3 仿真环境搭建

本文采用三维栅格地图对三栖环境进行建模，如图2所示。

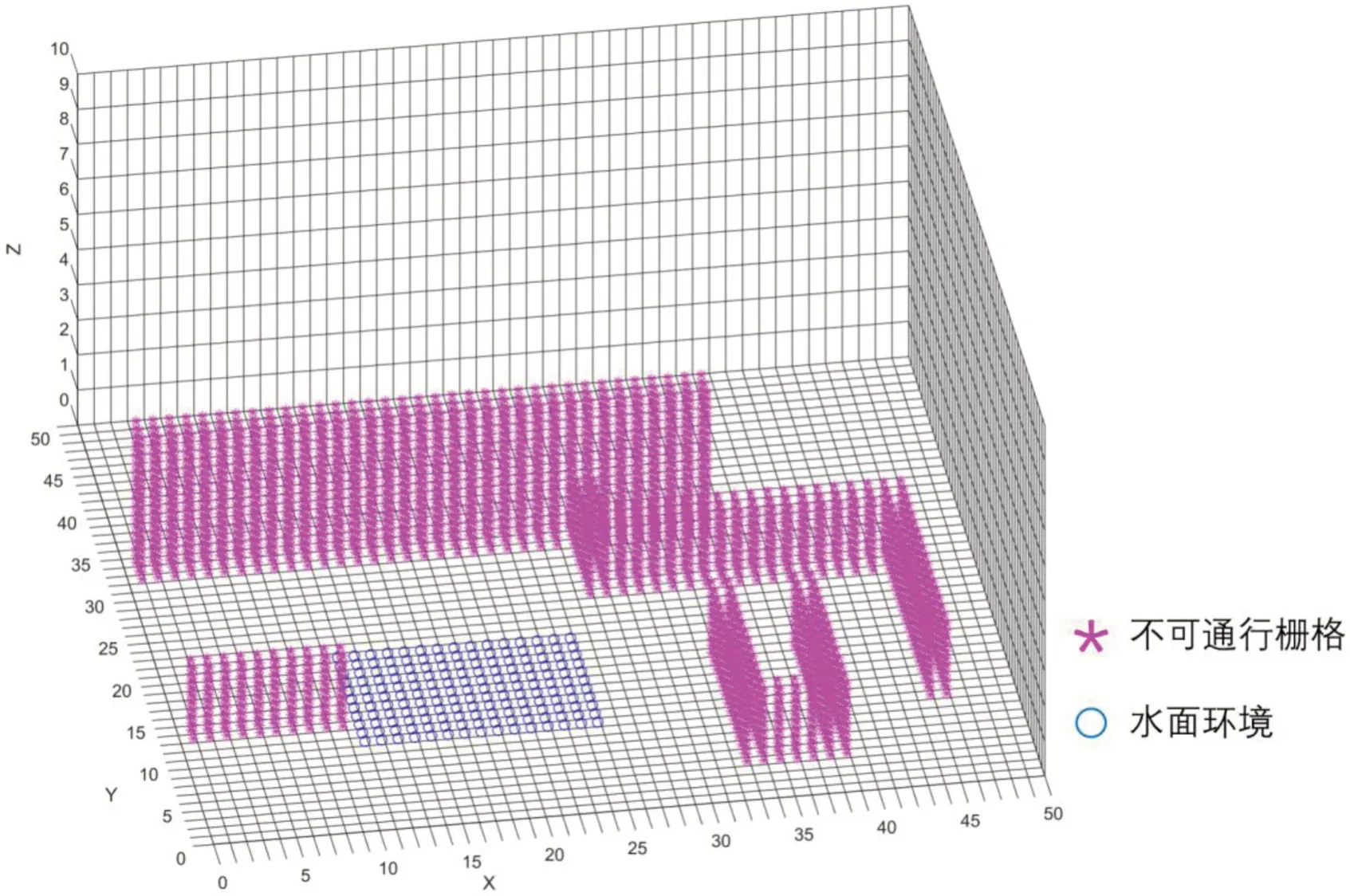
图2：三维栅格环境

选择空间中一固定点作为坐标原点， Z轴方向作为高度。在 Z 轴方向上，均匀将三维空间n等分，形成n个平面。每个平面沿着 X 轴与 Y 轴方向分别再n和n等分，则可以用 n×n×n个栅格来表示三维空间环境信息。每个栅格包含了栅格可通行状态和栅格空间类型，如水面、空中栅格或地面栅格。图3中，蓝色区域为水面栅格，粉色区域为不可通行栅格，Z=1的区域为地面栅格，其余为空中栅格。

图3：第1组实验轨迹俯视图

4 算法验证与分析

在MATLAB2018环境下，对改进三维A*算法进行路径规划的仿真实验。采用50×50×10的栅格地图作为实验的仿真环境。根据参考文献、文献、文献所提出的机器人的耗能分析并进行仿真实验，设置估价函数的参数为：

e=12.5, e=9, e=1, t=1,

t=6, t=13, κ=1.7

我们设置了三组仿真实验，第1组为能耗、时间权重分别为0.5、0.5的改进算法与原算法对比实验；第2组为权重分别为0.15、0.85的改进算法与原算法对比实验；第3组实验为权重分别0.5、0.5和0.15、0.85的改进算法之间的对比实验。

图3，图4为第1组实验仿真结果图，将目标点设置在水面中央。蓝色轨迹是传统A*算法，绿色轨迹是改进A*算法。传统A*算法规划时采用了从地面运动状态至飞行状态的方式飞跃障碍物，并保持飞行状态，在接近终点时，切换至水面运动状态后运动到目标点。改进A*算法规划的路径选择了维持地面运动状态绕开障碍物后，在面对水环境时，选择了综合代价较小的切换至飞行状态并向目标点。通过分析表2第1组实验数据，在当前耗能、时间权重和环境下，改进A* 算法规划的路径虽然路径长度和时间代价相对比较大，但是耗能代价明显小，且综合代价也更小，更利于降低机器人运动的成本。

图4：第1组实验轨迹立体图

表2：传统算法与改进算法对比实验数据

图5是第2组实验仿真结果图，将目标点设置在水面中央。蓝色轨迹是传统A*算法，绿色轨迹是改进A*算法，在第2组实验中，调大时间在代价分析中的权重，让机器人以更快的时间到达目标，而较小考虑耗能代价。传统A*算法规划时路径保持不变。改进A*算法选择了时间代价更小的路径，直接从起点飞过障碍物，且中间不再进行状态切换，也不再水面上运动，直接飞达目标点。通过分析表2第2组数据，在当前耗能、时间权重和环境下，改进A* 算法规划的路径虽然耗能代价相对比较大，但是运动时间代价明显小，且综合代价也更小，有利于机器人完成对运动时间要求比较高的导航任务。

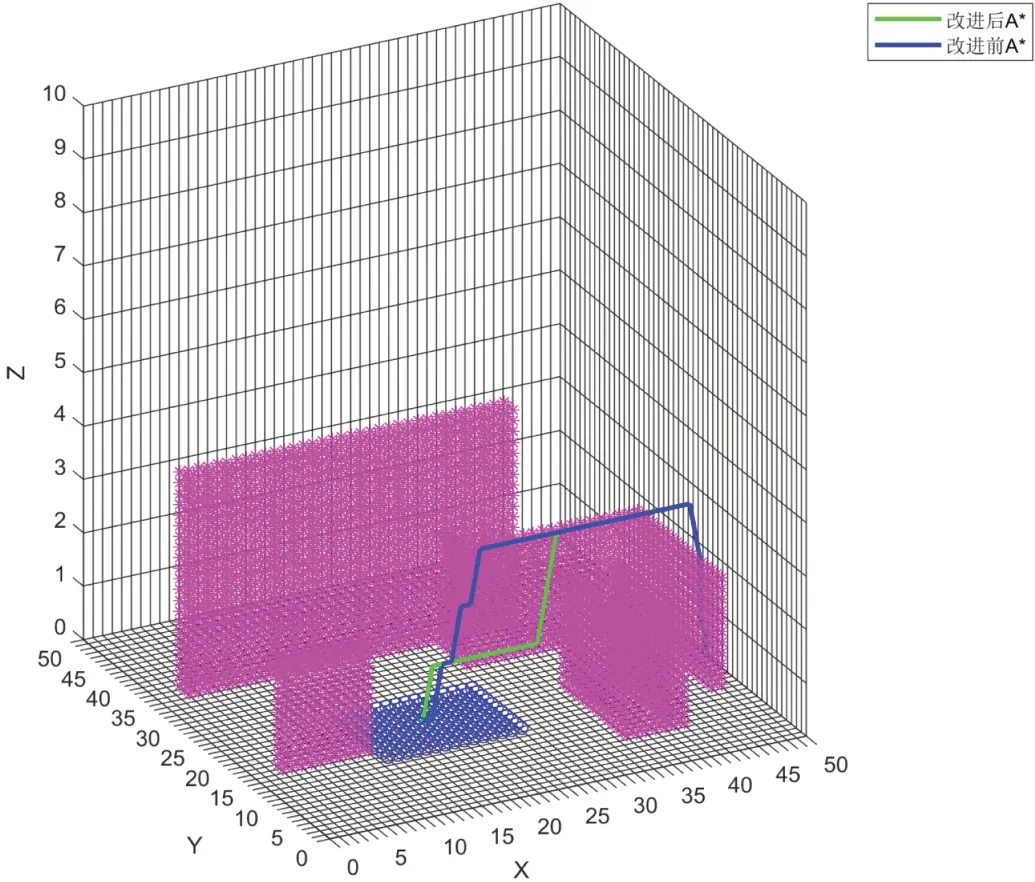
图5：第2组实验轨迹立体图

图6是第3组实验仿真结果图。绿色轨迹为能耗、时间权重分别为0.5,0.5的路径轨迹，蓝色轨迹为能耗、时间权重分别为0.15,0.85的路径轨迹。蓝色轨迹时间代价权重较大，因此在面对水环境时，选择直接切换至飞行状态，飞达目标点。而绿色轨迹降低了时间权重，因此面对水环境，并没有直接选择切换至飞行状态并飞达目标点这一时间代价较小的路径，还是选择了综合代价较小的切换至水面状态，经过水面环境后，切换至陆地状态运动一段时间。之后，算法比较了直接飞过障碍物和通过陆地运动绕过障碍的综合代价，选择了飞过障碍物这一综合代价较小的方式。表3数据表明，采取不同的权重，算法规划的目标不同，结果也不一样。可通过改变权重来改变规划目标。

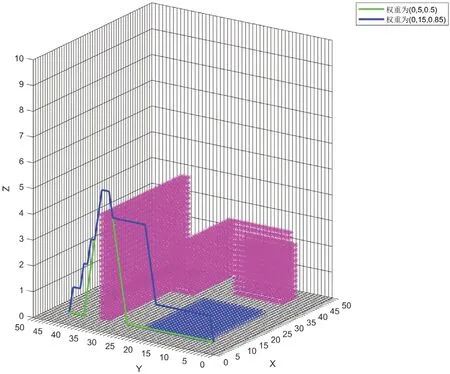
图6：第3组实验轨迹立体图

表3：第3组实验（不同权重的改进算法对比实验）数据

5 结语

本文研究并探讨了三栖机器人的广阔前景以及现有的路径规划方法的优点以及不足之处，在现有学者的只针对陆空环境的规划以及仅在突发环境下局部规划等研究成果的基础上，提出了基于运动状态以及状态切换的耗能分析和时间综合代价分析的改进三维A*算法，实现三栖机器人的全局路径规划。经实验验证，改进算法能够降低机器人运动的综合代价，且能够通过改变权重来使机器人执行特定要求下的导航任务，这对多栖机器人运动的研究具有一定的借鉴意义。

此外，对于26邻域进行搜索会导致算法的时间复杂度较高，可以考虑优先对相同环境属性或陆地属性的栅格邻域进行搜索，提高算法的时间性能。