奇异摄动内联线性系统的事件触发控制一致性
2022-09-09任祥万星袁峰张倩茹张智慧
任祥 万星 袁峰 张倩茹 张智慧
(中国航天科工集团第二研究院七〇六所 北京市 100854)
1 前言
网络化控制系统中网络资源的高效利用越来越成为网络化控制的研究重点。传统的周期采样控制以周期的方式采样并更新控制信号。作为替代周期采样控制的一种控制方法,事件触发控制把控制信号的更新与被控系统的控制性能结合起来,通过设计合理的事件触发条件来决定控制信号的更新与否。从而使得事件触发控制能在不严重损失闭环系统性能的前提下大量的节省系统中的计算资源与网络资源,使得事件触发控制成为变周期控制。已有大量相关的文献研究事件触发控制,如针对线性系统,非线性系统,扰动系统,多智能体系统等。
2 奇异摄动系统
奇异摄动系统是一类含有两个时间尺度的系统,从而使得系统状态可以分为快慢两种状态类型。奇异摄动方法是分析和研究奇异摄动系统主要方法。研究奇异摄动的主要问题涉及稳定性,镇定问题,H控制问题,基于模型的控制等。近年来,多智能体奇异摄动系统的一致性研究得到了研究人员的关注。多智能体系统的重要特点是局部信息在整个系统中起到了关键作用。多智能体系统的分布式控制是利用每个子系统的局部信息来达到控制目的,所以分布式控制一定程度上减少了对子系统之间的通讯与计算资源的利用。
已经有相关的文献考虑了奇异摄动系统的事件触发控制问题。文献考虑了有结构不确定性的奇异摄动多智能体的事件触发控制问题。文献考虑了有切换拓扑多智能体奇异摄动系统事件触发控制一致性问题。
在以上提到的文献中,没有基于积分信号和外部辅助动态设计的事件触发条件的相关研究。考虑到动态事件触发条件的采样性能和积分事件触发条件的采样性能各自的优点,针对奇异摄动多智能体系统设计基于外部动态和积分信号的事件触发条件,从而尽量节省计算和网络资源变得十分必要,但是在已有相关文献中很少有这类型事件条件的研究。
基于上述讨论,本文研究针对奇异摄动多智能体系统基于外部辅助动态和积分信号的事件触发控制一致性问题。基于奇异摄动方法,可以得到针对每个智能体动态的快慢子状态,利用每个智能体系统和辅助动态扩维形成的子系统设计基于动态和积分信号的事件触发条件,并且分析了闭环系统中的芝诺(Zeno)现象。
本文接下来的部分安排如下。在介绍一些必要的符号和文中通用的定义之后,接下来给出了问题的描述,紧接着给出了文中的主要结果。数值仿真部分利用数值实例来验证上一部分理论的有效性和可行性,最后在结论部分给出了本文主要结论。
2.1 符号定义

2.2 图相关理论

下面给出本文中用到的必要的定义、引理以及假设。


3 问题描述
考虑如下的系统:
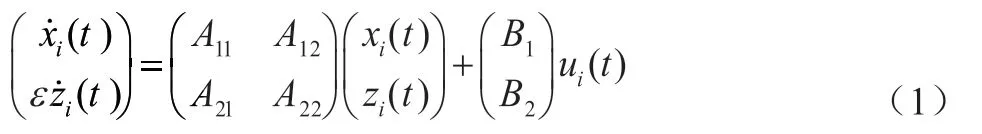

控制输入给出如下:

其中矩阵K,K待给出。定义状态x(t),z(t)的采样误差分别为:

依据文献的结果,多智能体系统(1)的一致性控制可以转化为一个镇定性问题,下面给出状态转化关系式。
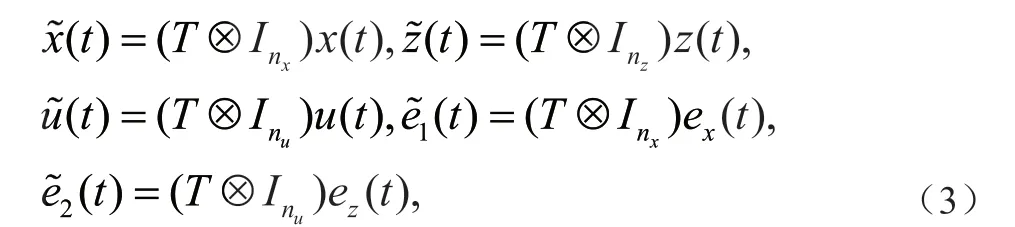
其中矩阵T在引理1中给出且x(t),z(t),u(t),e(t),e(t)的定义分别如下:
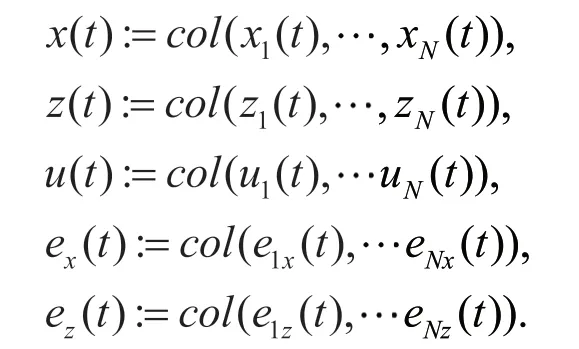
定义以下向量:

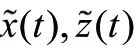

其中:

触发时间序列依据下面的事件触发条件给出。
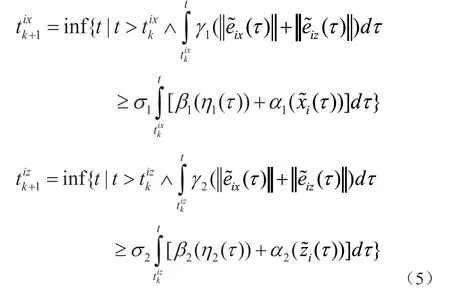

4 主要结果

对于系统(4),定义

其中
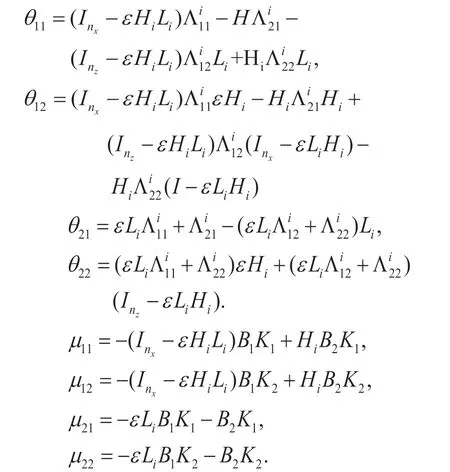

利用(10)中矩阵的解,(9)中系统矩阵与输入矩阵可以写为

基于假设2,给出以下定义。
定义2.矩阵K是使得矩阵A+BK为Hurwitz矩阵的增益矩阵。
引理2.对于系统(1)以及下面的控制器
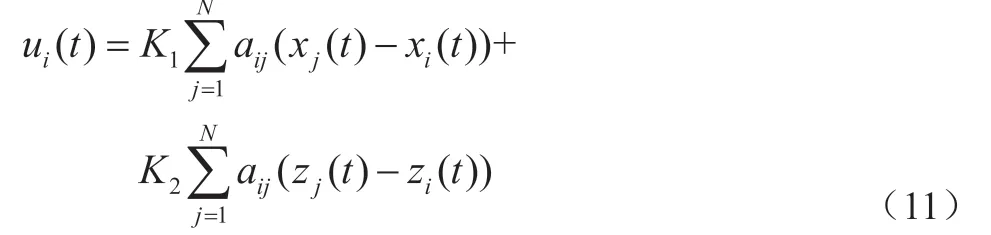
如果假设1与假设2成立,那么存在一个矩阵


和

和

可知触发条件(5)的触发间隔比基于积分的事件触发时间间隔大。基于文献中基于积分型事件触发控制可以避免芝诺行为发生的结果可知,事件条件(5)可以排除芝诺行为。
基于上述分析,在下面的定理中给出主要结果。
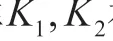
考虑到(8)和(3)的关系,定理1的结论同样可以应用到系统(1)。下面的推论中给出针对系统(1)的结论。


数值仿真
在这部分给出上一部分对应的仿真结果来验证理论的有效性与可行性。给出以下矩阵参数。
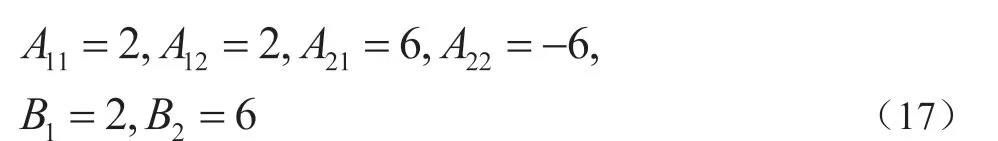
摄动参数ε取为ε=0.001,采样步长取为1×10,内联拓扑图如图1所示。
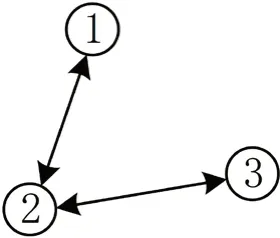
图1:内联拓扑图

由图2和图3的结果可知,闭环系统状态在事件触发控制的作用下最终趋于一致,由表1可知,各个时间条件的不同触发最小间隔都大于设计的仿真步长,表明闭环系统中不会出现芝诺行为。
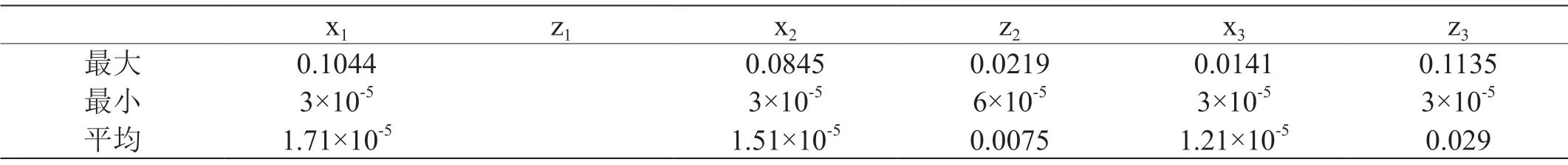
表1:采样间隔

图2:系统慢变状态轨迹

图3:系统快变状态轨迹
