模块化多电平换流器电热耦合模型研究

张鹭 李润秋

（国网陕西省电力公司经济技术研究院 陕西省西安市 710075）

模块化多电平换流器（modular multilevel converter,MMC）由A. Lesnicar和R. Marquardt于2003年首次提出，是一种非常有前途的拓扑结构，并且在全世界范围内得到了广泛的研究和关注。与传统的两电平和三电平换流器相比，MMC具有模块化，可扩展性，高效率和卓越的谐波性能等显着特征。因此，MMC在高压和大功率的应用领域具有广阔的发展前景，例如高压直流输电技术（HVDC），静态同步补偿器（STATCOM），直流配电网，电机驱动应用等领域。

在过去的几年中，许多关于MMC的研究主要集中在数学建模，控制策略，环流抑制和子模块电容电压平衡控制等方面。然而，在MMC运行过程中，由于热应力的影响，功率半导体器件更容易失效，其寿命受结温的影响。因此，功率半导体器件的功率损耗和结温的信息对于研究MMC非常重要。值得一提的是，在MMC系统的设计中，其功率损耗的计算起着重要的作用，直接关系到MMC运行期间的稳定性和可靠性。组成MMC的子模块结构可分为三种类型：半桥，全桥和钳位双子模块。MMC大多采用半桥子模块，因此本文以半桥子模块为主要研究对象。

文献提出了一种基于新型PWM控制策略的功率损耗和结温计算方法，分析了桥臂子模块的功率损耗和负载相角对子模块功率损耗分布的影响。文献描述了MMC功率损耗的详细计算方法，并分析了MMC和传统的两电平换流器之间的功率损耗情况。但是，该方法基于以下假设：MMC系统在最高温度下运行，并且开关频率与流过MMC的电流成比例。文献研究了MMC系统中各种因素对功率损耗的影响。文献提出了一种新的快速稳态模型来计算MMC的损耗，其中考虑了功率器件，电感和冷却系统的温度的影响。但是，此方法假定条件MMC中的子模块相同，子模块电容电压平衡且等于额定电压，并且不存在环流。这些假设将导致MMC系统的功率损耗计算不准确。文献提出了一种基于平均功率损耗模型的MMC时间较短的计算方法，该方法也可以扩展到不同的子模块和不同的调制策略。考虑到电热耦合效应的影响，文献提出损耗计算方法是基于MMC系统运行期间的结温反馈计算得出的，所提出的方法使功率损耗计算更加准确，并确保子模块在安全结温下工作。

本文提出了一种电热耦合模型来计算运行期间的MMC系统子模块中功率半导体的损耗和结温。通过拟合功率半导体的特性曲线，根据其通态压降，通态电流和开关能耗，以及从MMC仿真系统中测得的电流和电压变量来计算半导体损耗。然后，基于给定的初始环境温度，建立功率半导体的四届Foster型电热网络模型以计算其结温。提出的模型由MATLAB/Simulink建立。

1 MMC的基本结构和控制策略

1.1 基本结构

既有N+1个子模块电压电平的三相MMC拓扑如图1所示。MMC由三个相单元组成，每个相单元分为两个桥臂，分别称为上臂和下臂（用下标u和l表示）。N个子模块与电感串联构成一个桥臂。其中，L表示抑制环流的电感。交流侧MMC的j相（j=A，B，C）与电阻R和电感L连接。MMC的基本元件是子模块，由两个IGBT（以T和T表示）组成，同时并联一个二极管（由D和D表示）和一个直流存储电容C。其输出电压为零或电容电压U，由子模块投入或切除决定。

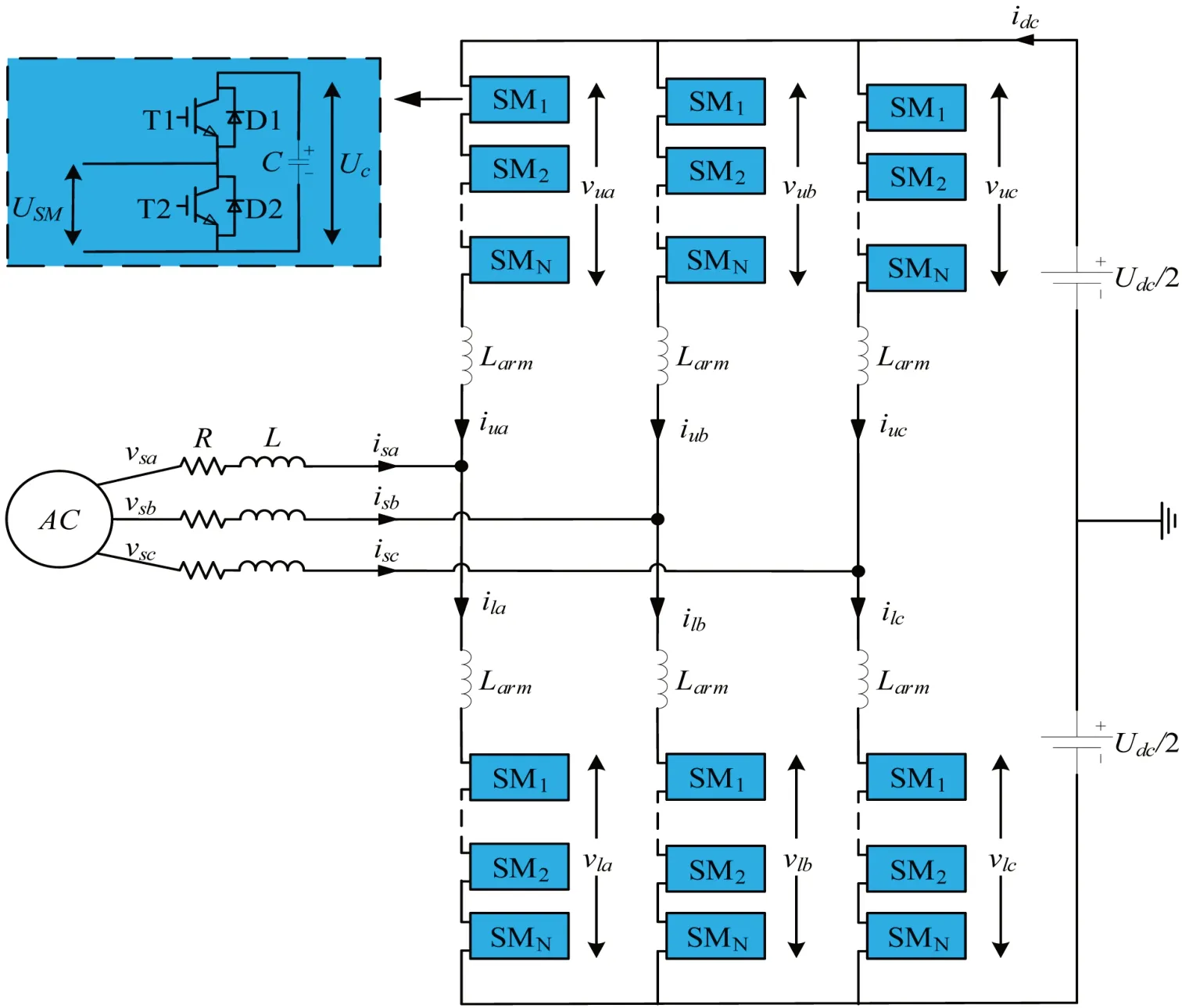
图1：三相MMC拓扑图

1.2 模型预测控制策略

在过去的几年中，模型预测控制（MPC）由于具有多个控制目标，包含约束和非线性以及快速动态响应等优点而被应用于MMC控制。但是，传统的MPC具有沉重的计算负担，因此处理器难以实现。结果，提出了改进的MPC来减少计算负担。本文采用图1所示的改进MPC用于控制MMC，子模块电容电压平衡控制策略采用常规的排序算法。

使用子模块电容电压排序算法的MPC策略的框图如图2所示，改进的MPC块策略的步骤可总结如下：

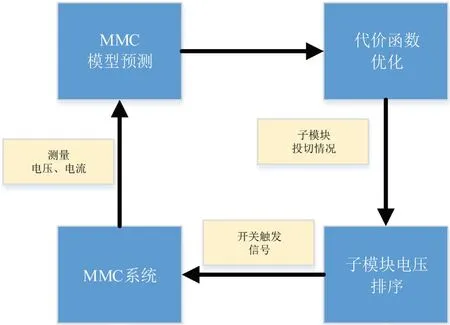
图2：模型预测控制框图

（1）从MMC系统测量的电流和电压变量。

（2）基于MMC离散时间模型预测的前一步变量。

（3）通过代价函数优化获得的插入或切除的子模块。

（4）通过子模块电容电压排序算法获得的开关状态信号来控制MMC系统。

2 电热耦合模型

IGBT模块是由不同成分的材料所构成，而不同材料间的热特性存在很大差异，最终导致IGBT模块具有复杂的热路。然而，为了获得快速准确的计算模型，为IGBT模块建立一个四阶Foster型电热网络模型，如图3所示。

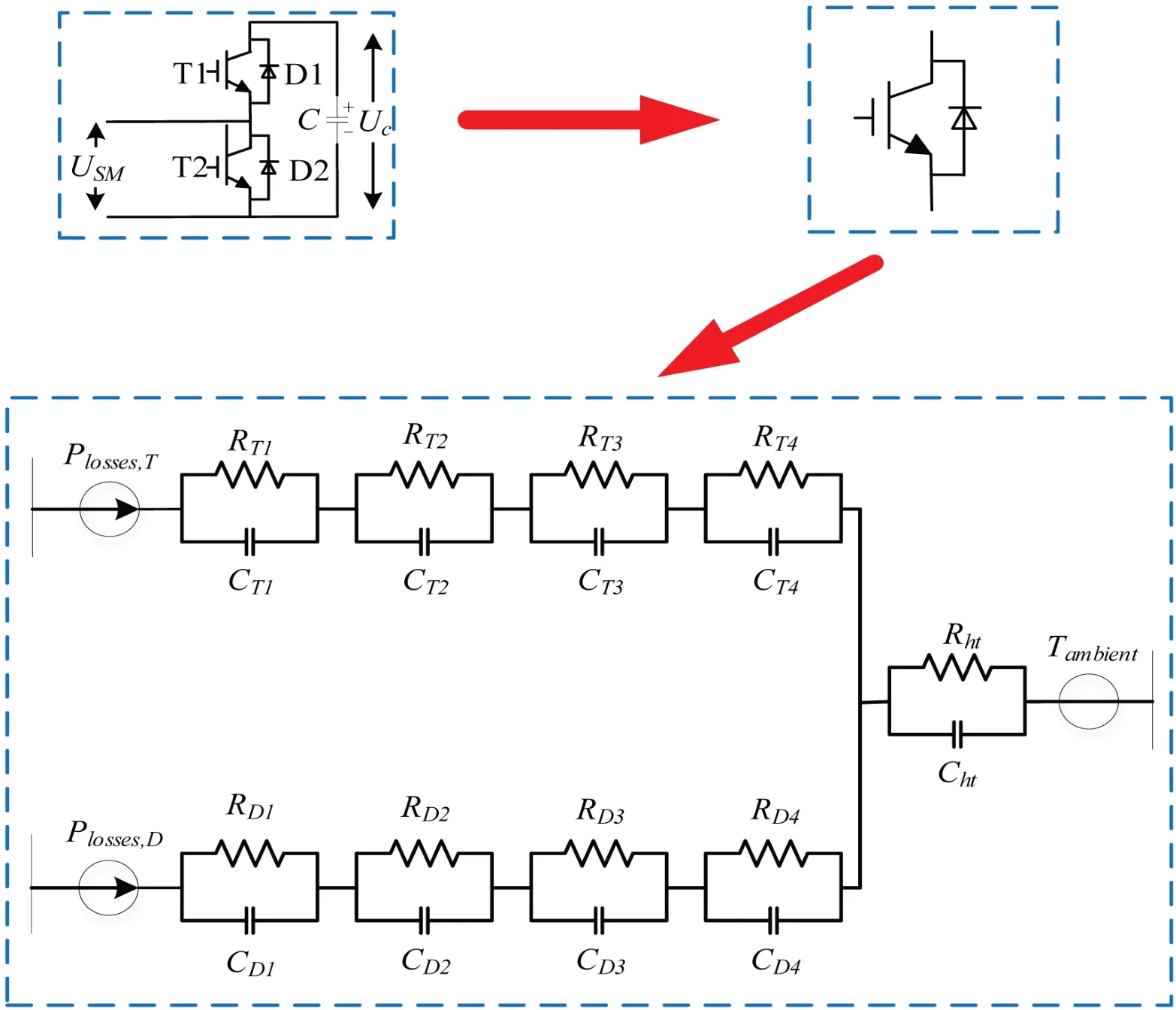
图3：半导体热模型

根据功率损耗和Foster型电热网络模型计算半导体的结温。如图3所示，R和C（i=1、2、3、4）是IGBT与外壳的等效热阻和热容；R和C（i=1，2，3，4）是二极管中芯片到外壳的等效热阻和热容。R和C是IGBT外壳散热的等效热阻和热容。T是环境温度。

根据电热比拟理论，半导体的热特性可以用热等效电路表示。半导体的结温计算如下：

其中Z和Z是结到外壳的瞬态热阻抗；Z和Z是外壳对散热器的热阻；T是散热器的温度。

3 仿真结果

根据图1，通过MATLAB/Simulink建立MMC仿真平台。本文对MMC系统的两种不同的运行条件进行了仿真。稳态过程的有功功率的参考值设置为3MW，MMC系统以单位功率因数运行。MMC系统的仿真波形如图4所示。

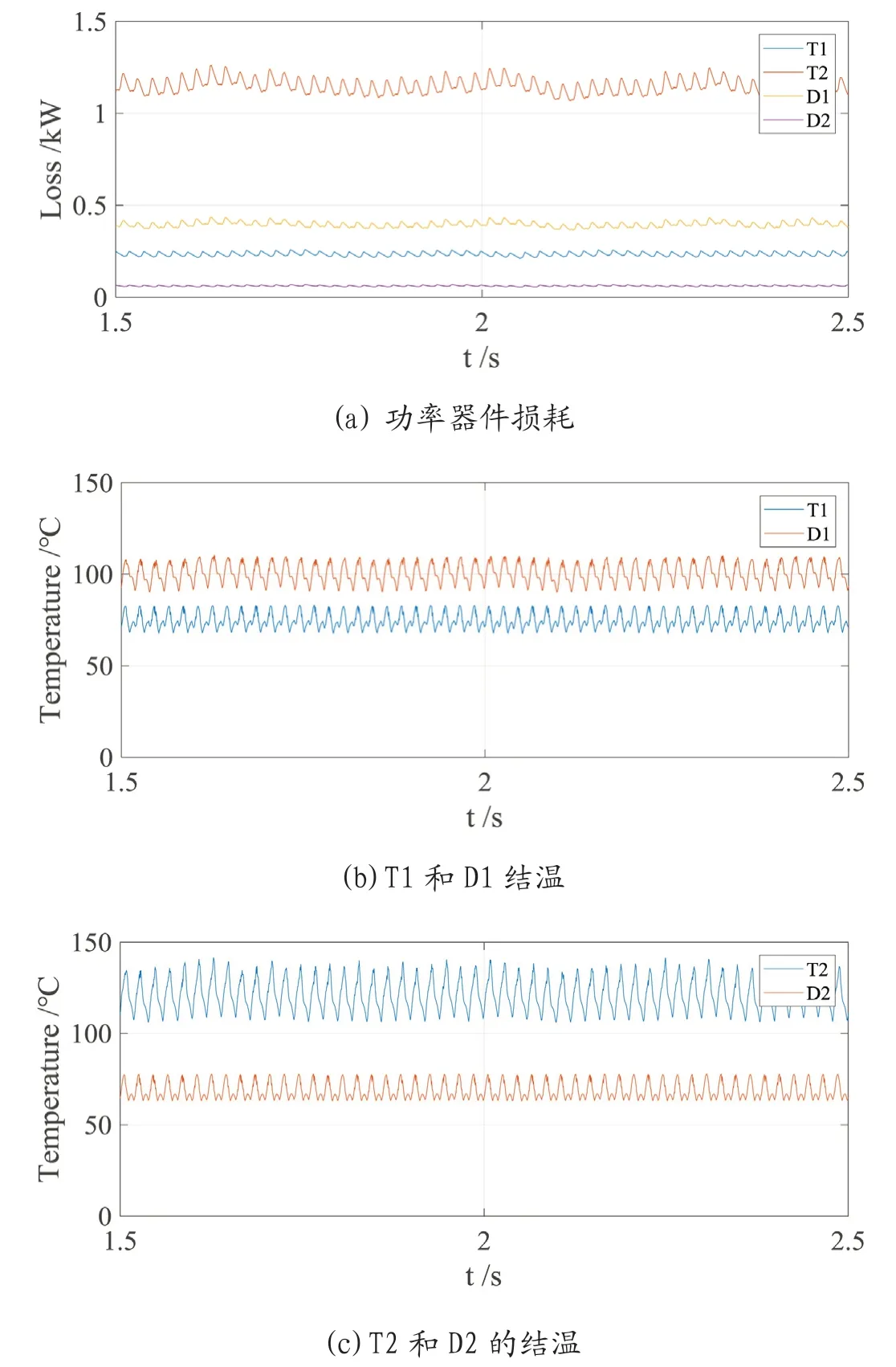
图4：MMC稳态运行波形

如图4所示，子模块中每个IGBT和二极管的损耗分布如图4(a)所示。从图中可以看出，IGBT和二极管的损耗分布不均匀。T2的损耗在1.1kW上下波动，且远大于其他半导体，因此，在器件选取过程中要着重考虑。而D2的损耗最小，对器件选取影响不大。图4(b)和(c)显示了稳态工作模式下子模块中上，下IGBT模块的结温。上IGBT模块中二极管D1温度最大，在100℃附近波动；下IGBT模块中T2的温度最高在125℃附近波动。半导体的结温都在安全允许范围（150℃）内。

4 结论

本文提出了一种基于电热耦合模型的MMC功率损耗和结温的仿真计算方法。通过拟合功率半导体器件的特性曲线，建立半导体器件的四阶Foster型电热网络模型，可以实时计算稳定状态和瞬时状态下基于模型预测控制的MMC仿真系统子模块中IGBT和二极管的功率损耗和结温，并能反映其动态条件下的损耗和结温的变化，为MMC的可靠性设计和应用提供了有效的参考。