基于改进梯度法的数字图像相关亚像素位移求解算法

董 一，王桂荣，洪 亮

（1.中国计量大学 机电工程学院，浙江 杭洲 310018；2.浙江传媒学院 电子信息学院，浙江 杭州 310018）

0 引 言

数字散斑相关方法（Digital Speckle Correlation Method，DSCM）是一种在20 世纪80 年代提出的非接触式的光学测量方法。它主要以应用电子学和光学的几个基本原理作为主要理论依据，将应用电子力学测试作为实验方式，通过采集试件变形前后的表面散斑图像，提取待检测区的灰度变化信息，分析并计算出物体表面的位移和应变场。随着现代电子科技的进步，摄像机的分辨率远超从前，这使DSCM 受到更多工程应用的青睐，使用范围更加广阔。现在已经有许多较为完善的亚像素搜索算法，如亚像素灰度插值法、梯度法、Newton-Raphson 迭代法、曲面拟合法、遗传算法等都是较为常用的。除了经典数学理论算法外，许多学者将群体智能优化算法引入到数字散斑相关法之中。遗传算法、人工神经网络算法、粒子群优化算法、果蝇优化算法都对数子散斑相关方法的研究起到了推动作用，但是这些方法都不完善。比如，遗传算法不能解决局部寻优的问题，并且计算复杂，编程繁琐；粒子群算法在捜索过程中容易出现陷入局部最优值，局部寻优能力也很差。

如今，无论是在材料力学研究、土木工程等传统领域还是在航空航天、军事设备、纳米科学以及生物医学等新兴领域，都对测量技术实时性、准确率和测量精度提出了更高的要求。目前的数字散斑相关法在理论研究上已经相对成熟，但是仍存在着一些不足。特别是在亚像素位移算法中，其精度不高，且耗时相对较长，对DSCM 的整体求解时间和计算精度有着直接影响。针对这类问题，本文根据双三次插值和梯度法的特点，提出一种改进算法。本算法在没有大幅提升计算量的情况下，减少了整体解决方案的时间，提高了计算精度，以便可以在各种工程领域得到更好的应用，切实解决实际工程问题。

1 相关工作

1.1 灰度插值法

在进行整像素位移搜索时，通常设置的搜索步长最小也是整像素级别的，故最终的搜索结果最高精度也只能达到1 pixel。为了达到更高的精度，可以通过灰度插值法对图像进行插值，在每两个像素之间插入4 个点，就可以将精度提高到0.2 像素级，插入9 个点，就能提高到0.1 像素级。以此类推，插入的点越多，达到的精度也就越高。不同的插值方法，得到的图像也不相同。为了能使后续搜索有较好的精度及效率，应选择一种合适的插值方法。灰度插值法有多种，较为常用的有最邻近插值、双线性插值和双三次立方插值。其中双三次立方插值的插值效果较好，插值后的图像亚像素点近似连续。双三次立方插值方法的原理如图1所示。图中，，分别为像素点的横向坐标值和纵向坐标值。

图1 双三次立方插值原理示意图

双三次立方插值根据点(,)周围邻域16 个整像素点的灰度值，通过设置好的加权系数计算加权平均值，从而得到点的灰度值(,)。高阶的插值方法效果比低阶的效果更好。令(,)=(+,+)，则点的灰度值计算公式如下：

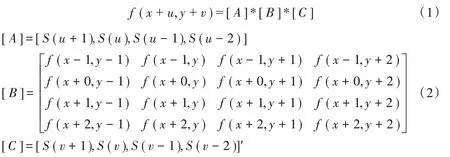
式中(·)为插值核函数。

利用Matlab 编程对模拟散斑图的相关系数主峰进行双三次立方插值运算，使像素值精度达到0.1 pixel，效果如图2所示。

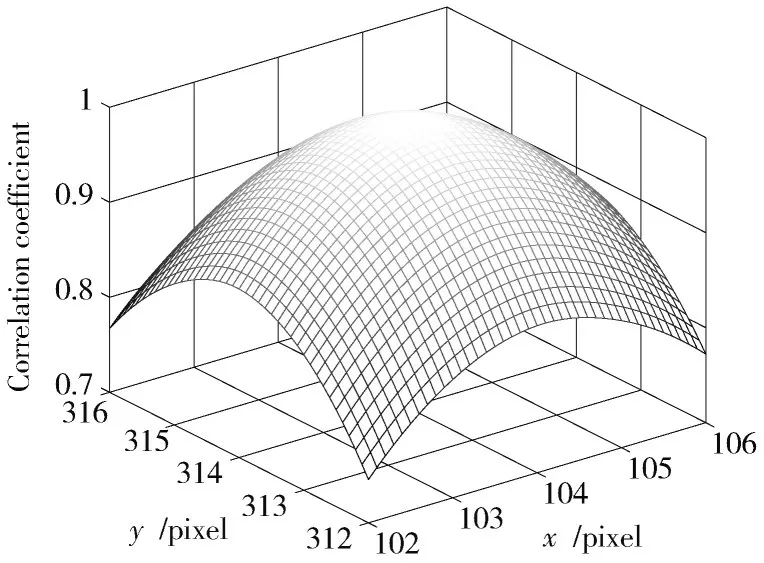
图2 双三次立方插值相关系数图

尽管灰度插值的方法能对图像进行重建，但得到的图像中的灰度值只是计算机模拟出来的，并不能完全到达实际预期。此外，灰度插值法对噪声及光强较为敏感，细微的干扰都会造成较大的误差；而且插值的计算量较大，导致计算时间较长。因此，插值的方法很少单独应用在数字散斑相关法中。

1.2 基于梯度的亚像素配准算法

基于梯度的亚像素位移搜索算法，最初是一种光流计算法，后被Freeman 应用到图像配准。该算法主要是根据散斑图像之间的灰度分布进行搜索，为了提高精度，还依据了其他特性。

该算法在以下两个条件成立的情况下使用：

1）图像灰度值不变：试件受到外力而形变时，试件表面图像中的灰度值不会随之改变；

2）试件刚体运动：在试件细微运动时，如果图像的参考子区非常小，该部分的点运动方向及距离都近似相同，那么此时参考子区的运动默认为刚体的平移运动。

分别用(,)和(′,′)表示物体发生位移前和位移后的图像灰度值，若子区图像非常小而且做细微运动，则有：

式中：′=++Δ,′=++Δ，,分别表示试件在，两个方向上的整像素位移，Δ,Δ分别表示试件在，两个方向上的亚像素位移。然后令式（4）中的(′′)对Δ,Δ进行泰勒展开，将高阶分量省略后能够得到：

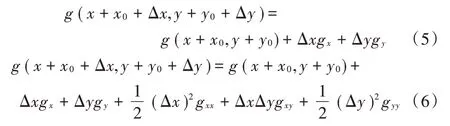
式（5）与式（6）分别是式（4）的一阶泰勒展开公式和二阶泰勒展开公式。显而易见，二阶泰勒展开后需要计算的数据更加多，计算时间也更长，故实际应用中一般选用一阶泰勒展开。式中的度梯g，g计算选择Barron算子，相比其他算子，该算子计算出的结果更加准确，也有较好的性能。其表达式如式（7）。

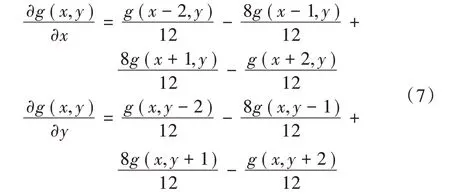
结合上述的公式，将目标函数设为：

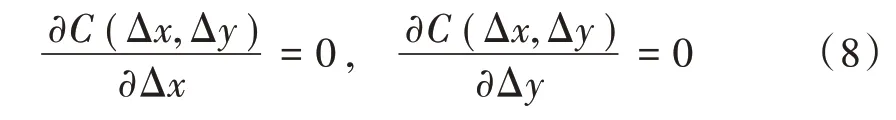
由式（7）、式（8）可计算出参考子区和目标子区（子区大小为×）的亚像素位移值Δ,Δ为：

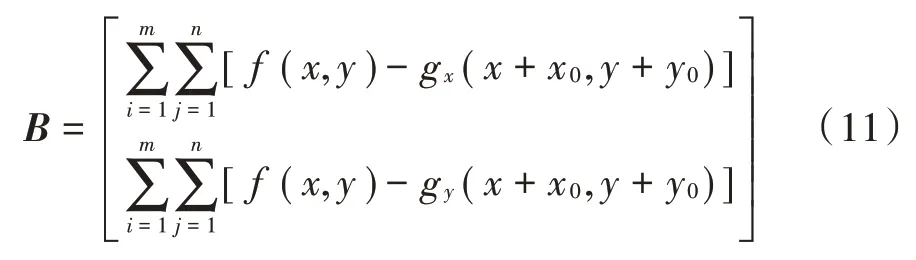
根据之前已经搜索得到的整像素位移，，就能够求出物体表面变形前后的散斑图像之间的亚像素位移值。梯度法有较为清晰的数学理论支持，其算法也并不难以实现，计算出的结果也较为精确，但是该算法也存在着缺点。当待求解的亚像素配准点的灰度值(++Δ,++Δ)在整像素配准点+,+的位置通过一阶泰勒公式转化时，为方便计算而舍弃了高阶小量，导致产生的误差会受Δ,Δ的影响，Δ,Δ越大，产生的误差也越大。虽然二阶泰勒展开公式带来的误差相对较小，但是计算过程会更加繁琐，消耗的时间也相应地增加。因此，当亚像素位移值Δ,Δ超过一定范围的时候，(++Δ,++Δ)的一阶泰勒展开公式的误差就会对结果造成较大的影响，最后获得的亚像素位移值并不能达到理想的效果。

2 基于灰度法的亚像素位移测量改进算法

2.1 理论依据

若想通过灰度插值法使搜索结果精确到0.01 pixel，则要在每两个像素点之间插入99 个点，将图像放大1 000 倍，此时两个子区图像也被放大，计算相关系数的消耗时长将呈几何式的增加。灰度插值法以增加计算量为代价提高计算精度，付出的代价超过了获得的效果，故并不建议使用。基于梯度的亚像素配准算法可以通过简单的编程实现，计算出的结果也较为精确，但是该算法的计算精度受限于泰勒公式展开时带来的误差，展开位置的亚像素位移值越小，高阶分量也就越小，此时搜索到的亚像素配准位置才精确。

本文提出的基于灰度插值法和梯度法的亚像素改进搜索算法，主要目的就是如何将这两种方法结合起来才能发挥各自的优势，消除它们的弊端。首先，在搜索的整像素配准点的基础上，通过双三次立方插值法搜索到精度为亚像素的配准点坐标；然后在该点的位置上对基于梯度的灰度搜索算法的公式进行一阶泰勒展开，由于粗配准点与最终配准点之间的坐标小于0.1 pixel，此时舍弃的高阶分量非常小，搜索结果的精度得到了有效的提高。该算法的原理及流程如图3、图4所示。图中点为整像素匹配点，点为亚像素粗匹配点，点为亚像素精匹配点。

图3 混合亚像素位移算法原理图

图4 混合亚像素位移算法流程

2.2 混合算法的计算公式

首先，通过整像素搜索算法快速搜索到整像素配准点，即找到相关系数曲面的主峰位置，以该点为中心对参考子区和目标子区进行插值重建。出于对计算时间和梯度法的精度考虑，选择在每两个像素点之间插入4个点，即将图像放大25倍，此时的亚像素搜索精度可达0.2 pixel，且消耗的时间不会过长。在参考图像中选取整像素配准点为中心点，截取大小为21 pixel×21 pixel的区域作为子图像，通过双三次立方插值对子图像进行插值后，得到大小为101 pixel×101 pixel 的图像，如图5所示。插值后的相关系数图如图6所示。

图5 双三次立方插值效果图

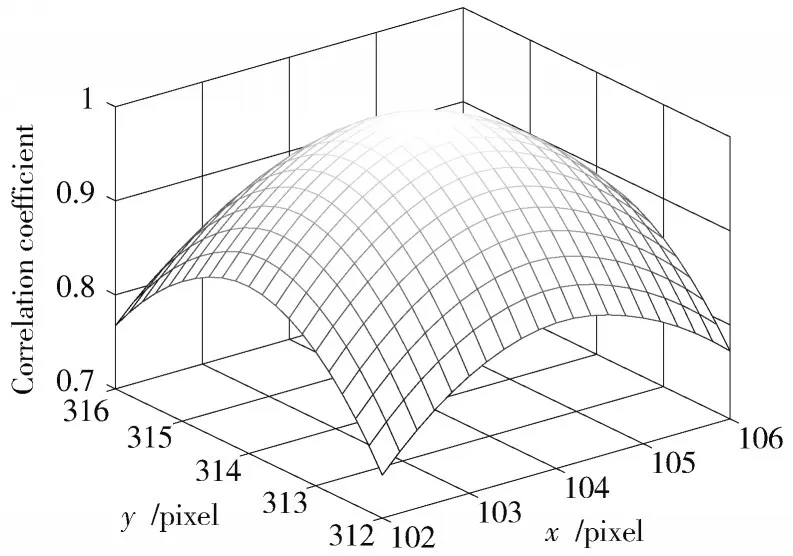
图6 双三次立方插值相关系数图（混合算法）

在对插值后的图像搜索得到粗精度匹配点，再以点为中心，对插值后的图像子区域通过基于梯度的灰度搜索算法搜索到最终的亚像素匹配点。目标函数及目标函数求极值公式如式（8）、式（9）所示，式（4）转化为式（12）：

式中：Δ,Δ分别为与之间的坐标差值；，分别为目标点与粗匹配点之间的坐标差值。因为Δ,Δ精度可达0.2 pixel，所以，小于0.2 pixel，缩小了梯度法中的高阶小量，有效提高了搜索精度。

经过计算：

代入已经计算得到的整像素配准点(,)和亚像素粗配准点(+Δ,+Δ)，求解出物体表面形变前后在图像中的位移，再通过标定系数，即可知现实中的位移，其中，为匹配区域的长和宽。

3 实验验证

3.1 算法的精度与计算效率

首先通过Matlab 制作1 幅散斑图像作为实验的参考图像，其大小为512×512，图中共有1 200 个散斑，散斑的大小设为4，散斑的亮度最高为1。同时通过参数设置，使参考图像沿方向做平移运动，总共平移1 像素，每次平移距离为0.05 pixel，生成1 幅新的散斑图像，最终得到19 幅模拟散斑图，作为目标图像组。在通过三步搜索法搜索到整像素配准点后，分别用4 种亚像素搜索算法计算目标图像组的位移值。由于单点进行搜索可能会存在偶然性误差，故在参考图像中都随机选择100 个目标点，对每幅目标图像都进行100次的搜索，并对结果进行分析，舍去异常的值。学者Zhang 经过研究发现后指出，将亚像素搜索窗口大小设在31 pixel×31 pixel～51 pixel×51 pixel 范围内时，各算法在计算精度和效率上都能保持较好的效果。故本文所有实验中，在进行亚像素搜索时搜索窗口设为41 pixel×41 pixel，效果如表1、表2所示。

表1 四种亚像素位移测量运算时间 s

表2 四种亚像素搜索法的位移测量结果 pixel

表1 中的运算时间以曲面拟合搜索耗时为基础单位，其中曲面拟合算法的运算速度是最快的，是因为该算法的拟合点只有9 个，不需经过复杂的运算；梯度法所消耗的时间是曲面拟合法的1.5倍，相差不多；而双三次立方插值法的耗时是曲面拟合算法的256 倍，效率过低，改进后的算法耗时为11.8 s，但远低于插值法，在可接受的范围内。

从表2 中可以看出在位移很小时，梯度法和改进后的混合算法的效果较好，在整个位移过程中改进后的混合算法的测量精度达0.01 pixel，并且整个过程中改进后的算法稳定性也较好。4种算法的性能比较如图7所示。

图7 各个算法搜索均值误差对比图

由图7 可看出，曲面拟合法的搜索结果的均值误差曲线变动幅度较大，灰度插值法的性能比曲面拟合法有所提高，梯度法和改进后的混合算法的效果较好。在0.4～0.8 pixel 范围内，改进后的混合算法更优于原来的梯度法，这是因为在这个范围内，梯度法在一阶泰勒公式展开处舍弃的高阶小量的误差过大。

3.2 刚体平移实验

为了检验改进后的算法在实际应用中的性能，进行了刚体平移实验，本次实验标定系数为0.537 mm/pixel。实验平台如图8所示，采集到的散斑图像局部放大图如图9所示。

图8 刚体平移实验平台

图9 散斑图像局部放大图

控制直线电机多轴运动平台（电机精度为0.05 µm）每次位移0.2 mm，每位移一次拍摄一张照片，共拍摄6张图像。对采集到的散斑图像用混合算法进行位移测量。图10～图12 为位移0.4 mm 时的，方向位移云图和总位移矢量图，其结果与实际位移方向一致。

图10 x方向位移云图

图11 y方向位移云图

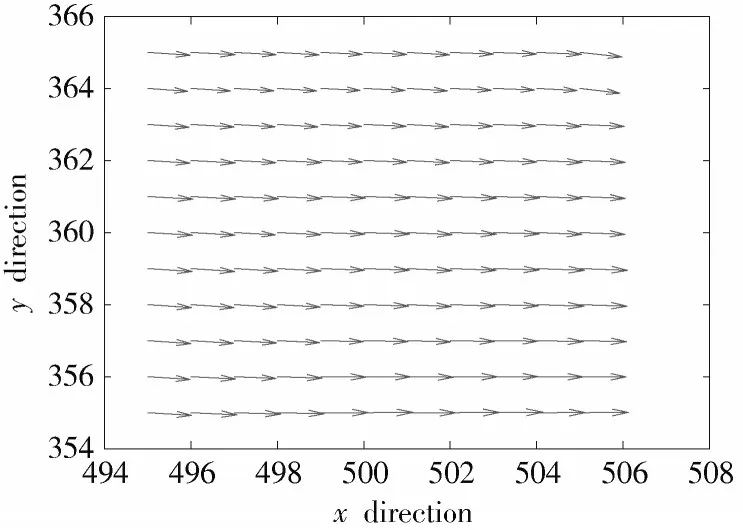
图12 位移矢量图

计算结果如表3所示，且给出了与理论值（实际平移值）的比较。

表3 不同平移条件下的计算结果

根据表3 中的数据显示：在不同位移的情况下，本文搜索算法的测量结果与实际平移值间的误差较小，在0～3%之间，说明测量精度较高；通过标准差可以看出，改进后方法的稳定性较优。综上所述，本文的搜索算法在实际应用中也有较好的性能。同时还利用另外三种算法进行实验，计算结果及耗时见表4。

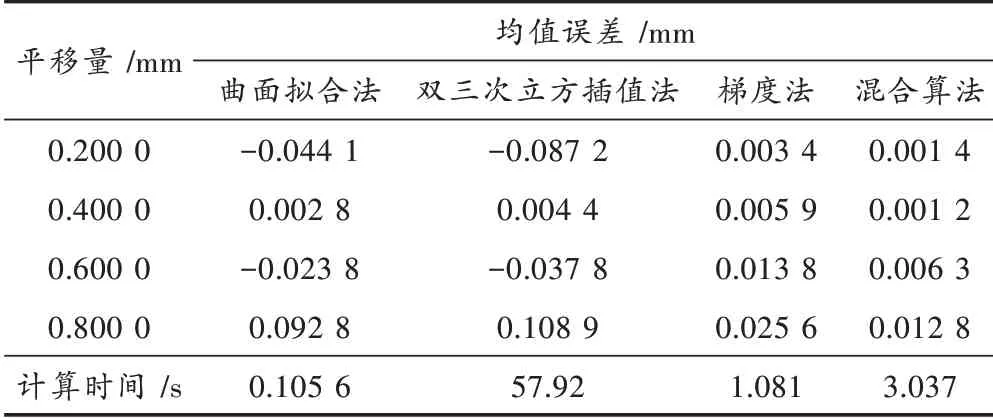
表4 不同算法的搜索性能

由表4 中的数据可以看到（计算时间是搜索目标图像中100 点消耗的总时长），在实际应用中本文搜索算法的精度高于其他三种，并且该方法的计算速度较快，能满足现场的实时性要求。

4 结 语

本文主要在灰度插值法和梯度法的基础上进行了改进，提出了一种灰度插值法和梯度法混合的亚像素搜索算法，通过插值法降低高阶分量引起的误差，从而提高梯度法的精度。通过软件编程进行仿真实验并搭建平台进行了刚体平移实验，并且对实验数据进行处理和分析。在搜索速度和计算精度两个方面，本算法相比双三次立方插值法、曲面拟合法和梯度法的整体性能更优。因此，本文提出的改进算法使数字散斑相关法可以满足实际工程中的高精度搜索要求，推进数字散斑相关法的研究。

本文主要是在二维平面的情况下，对数字散斑相关法进行了分析研究，忽视了离面位移对计算精度的影响。但在实际应用中，离面位移还是会引起误差，接下来的研究中可以考虑将该方法从二维平面发展到三维平面，不仅能检验离面位移的影响，还能使数字散斑相关法应用到新的领域中，如机器人的双目识别等。