有关复变函数中一类复积分的研究

荆柏瑞，庞慧慧，陈 静*

（1.中国农业大学信息与电气工程学院，北京 100083；2.中国农业大学理学院，北京 100083）

0 引言

《复变函数》[1]是我国高等院校工科专业，特别是电气工程及其自动化、电子信息工程、通信、自动化、热能与动力工程、测控技术与仪器等专业必修的重要基础课程，是学好相关专业课程的基础，是解决流体力学、电磁学、热学及工程力学等领域中平面向量场问题的有力工具。在学习时，要求学生具备《高等数学》及《线性代数》的理论基础，具备一定的逻辑抽象能力及运用数学观点分析问题、解决问题的能力。

在“跨学科融合”及“点线面体”等教学新模式[2-4]研究下，注重学生思维的延拓性、发散性、方法的多样性和创新性的培养。复积分是复变函数中一个非常重要的内容，其中一类复积分的研究难度非常大，文章结合代数、几何及分析等方法，从不同角度反复思考、分析问题，深入挖掘问题中隐含条件，以新颖独创的方法解决该类问题，给出了非常全面且更有意义的教学研究途径及方法。

1 问题提出与分析

问题（1.1）：求一类复积分[1]

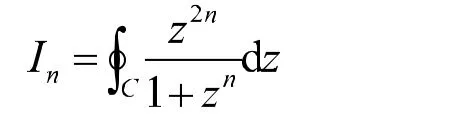
2 多种研究过程

2.1 利用函数在无穷远点处留数与在圆环域内洛朗展开式的系数关系研究问题（1.1）

2.2 利用函数在无穷远点处留数与在原点处留数的转化关系研究问题（1.1）

2.3 利用有限奇点处的留数研究问题（1.1）

2.3.2 借助n为偶数情况辅助去研究（6）式

由于该方程得到的复根在复平面上对应的点刚好是以原点为圆心单位圆的内接正n边形的n个顶点。利用复数的向量表示法与向量合成法则可知，n为偶数时，对任意一个根，必然存在一个与其关于原点对称的根，故

3 结论

通过对复变函数中难度非常大的一类复积分多方面展开研究，多角度得到了一致性的结果，既可以在教学研究过程中引导学生变换角度思考问题，利用自己擅长的领域对复杂的问题进行剖析，取得更好的教学研究效果，同时鼓励学生在学习的过程中要通过不同角度研讨问题，今后遇到问题时，不拘泥于现有学科的分析思路或已有的解决方法。引导学生充分调动学习积极性，打通不同课程间的知识壁垒，灵活应用所学知识解决实际问题。