接入风光电的水电机组振动信号分析与故障诊断方法研究

任 岩，张琳琳，刘金伟，齐 坚，崔换霞

（1．华北水利水电大学电力学院，河南省郑州市 450045；2．黄河勘测规划设计研究院有限公司，河南省郑州市 450003；3．中广核工程有限公司，广东省深圳市 518100；4．河南水投水土资源开发有限公司，河南省郑州市 450000）

0 引言

随着“十四五”时期“双碳”目标的提出，大力发展清洁可再生能源成为电力行业发展的重要举措。考虑到水电的清洁性、灵活性，未来水电与新能源联合发展具有很大潜力。然而，水电机组作为水电能源转换的关键设备，正朝复杂化、巨型化方向不断发展，各部件间的耦合作用更加强烈，故障与征兆间的映射关系更为复杂[1]。

常规水电振动往往由水力、电气、机械三方面耦合影响，风光接入下的水电机组振动更加复杂。根据统计显示，80%的水轮发电机组故障都会在振动信号中体现出来，机组的振动水平是衡量机组运行质量的重要指标[2]。因此，对振动信号进行故障诊断，可以实现机组的状态检修，保障机组安全、稳定运行。而水电机组所处的环境较为复杂，传感器采集到的振动信号往往被大量噪声所淹没，因此，采集到的振动信号需进行降噪的预处理，并进行特征提取和故障诊断。近年来，国内外的学者针对机组振动产生的非平稳性、非线性信号提出一系列的信号处理方法，如小波变换[3]、经验模态分解[4，5]、变分模态分解[6，7]、奇异值分解等[8]，通过一系列特征提取及信号重构可以有效地去除噪声，判断机组故障部位分析原因，以规避故障发生。

针对上述问题，本文围绕水电机组振动进行分析，从水、机、电方面综合分析常规水电机组的振动原因，并分析接入风光电的水电机组的振动情况。考虑到时域或频域的信号处理方法无法适应振动信号的非平稳性与非线性，本文对国内外时频域信号处理方法和故障诊断技术进行综述，探究现有方法中存在的理论和应用不足，并对未来发展提出看法。

1 常规水电机组振动分析

1．1 水电机组结构与工作原理

水电机组主要由水轮机、轴系和发电机等关键部件组成。水轮机部分包括底环、导水机构、转轮体、支持盖等；轴系部分包括主轴、操作油管、水封、水导轴承和推力轴承；发电机部分包括发电机定子、发电机转子和机架等[9]。在水电机组运行过程中，以上部件都直接或间接地参与了电能的转换，同时各部件产生的振动、疲劳及气蚀都将会影响机组寿命造成安全经济损失。

水流通过引水管道进入，冲击水轮机叶片，使水能转化成旋转的机械能。水轮机转动带动发电机运转，使旋转的机械能转化成电能。水轮发电机组实现了水能—机械能—电能的转换。

1．2 常规水电机组振动原因

机组运行过程中受到各种干扰力的影响不可避免地产生振动，异常振动会产生噪声与气蚀破坏、引起共振、导致机组零件疲劳，影响机组的运行状态，破坏机组稳定性。分析产生振动的原因具体如下[10]：

（1）水力振动因素：尾水管低频涡带；卡门涡列；蜗壳和导叶等过流部件流场不均匀；水轮机密封处产生的水力不平衡以及水轮机过渡过程中的其他不稳定因素。其中，尾水管涡带振动是引起水力振动的主要因素。

（2）电气振动因素：转子磁极绕组匝间短路；转子磁极形状有差别；定子铁芯松动引发振动；转子定子铁芯间气隙不均；发电机不对称工况下运行；产生负序电流；磁极分布圆中心与旋转中心偏离较大。

（3）机械振动因素：导轴承缺陷或间隙调整不当；机组轴系与支承结构刚度不足；质量不平衡；大轴扭曲；轴承不对中等。

机组振动可能是由水力、机械、电气单方面因素引起，也可能由以上三种因素耦合引起。尽管导致振动的原因有多种，但它们之间却互相联系、互相影响。

2 接入风光电的水电机组振动分析

2．1 接入风光电的新型电力系统

以风光为代表的新能源清洁无污染且可再生，构建新型电力系统是实现能源结构低碳转型的重要保障。但风光的强随机性与波动性影响电网稳定运行，加重了电网调节负担[11]。新型电力系统中风光等新能源的高比例接入需要配置可调性电源来提高负荷快速调节能力[12]。

考虑到水电的清洁性及灵活调节性，可以将水电与风光电互补发电来平抑新能源出力波动。为了与风光形成出力互补，水电往往承担能源调节角色配合风光发电，如图1所示。

2．2 接入风光电的水电机组振动

接入风光电的水电机组需要更加频繁地启停配合风光波动，造成多变工况下水电机组的工作环境与运行状态更为复杂。水电机组偏离最优工况进入振动区运行，具体表现如下：

（1） 加剧常规振动：接入风光电后水电机组工况转换频繁，使水流紊乱产生气蚀、涡带等现象，形成压力脉动加剧尾水管等部位的振动。

（2） 引起异常轴系振动：调速器只可保证在最优工况下对发电机角速度的调节。风光接入后，机组在偏离最优工况的振动区运行，无法调节轴系振动，造成机电设备的破坏。

（3） 影响机组水力结构性能：机组的水力不平衡会加大叶片裂纹、加剧疲劳破坏、增大厂房等基础设施的磨损。

（4） 产生水锤现象：在复杂工况下的机组频繁启停会造成机组的开度多变使水压多变产生水锤，加剧了机组出力调节难题。

振动信号往往反映机组的故障原因，基于对常规水电机组与接入风光电下水电机组的振动分析，对振动信号采集并进行故障诊断可以实现机组运行效率的最大化并减少经济损失。

3 非平稳振动信号的故障诊断研究

对机组故障及时处理可以保障机组安全稳定运行，延长机组设备的使用寿命[13]。在互联网快速发展的背景下，智能化在故障诊断中得到了极好的应用[14-16]。但采集到的振动信号往往被噪声掩盖，对故障诊断产生干扰，所以要对信号进行降噪预处理。图2、图3为水轮机尾水管振动信号降噪前后对比图，观察发现经过降噪处理后波形毛刺减少，反映故障特征的频率基本被有效提取了出来。针对振动信号的非平稳性与非线性，国内外学者提出一系列的时频信号处理方法。这些信号处理方法经过变换与重构可以有效提取故障特征便于后续分析。图4为非平稳振动信号故障诊断的流程图。

图2 噪声干扰下的尾水管振动信号图Figure 2 Plot of tailpipe vibration signal under noise disturbance

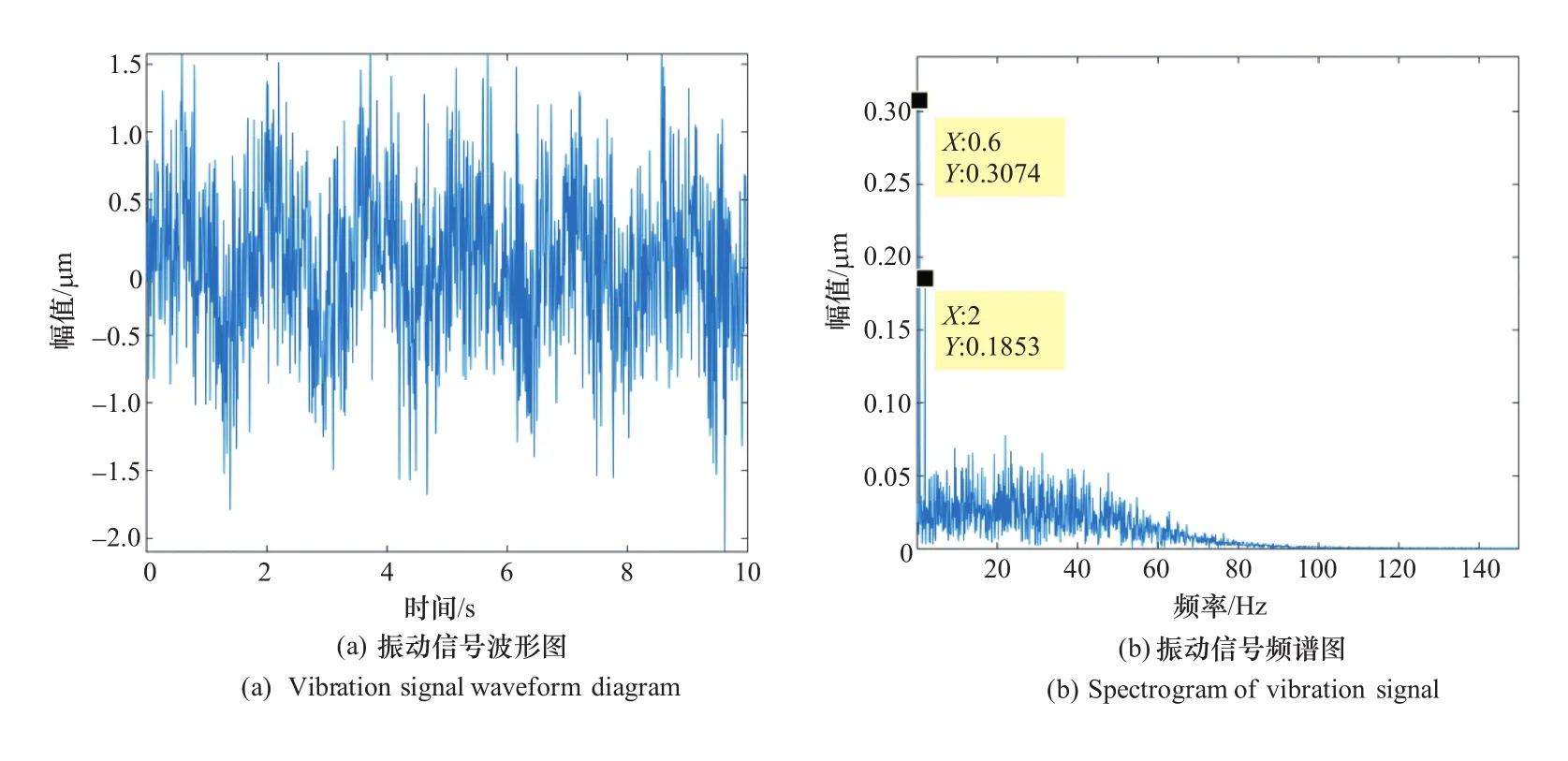
图3 降噪后的尾水管振动信号图Figure 3 Vibration signal diagram of the tailpipe after noise reduction

图4 非平稳振动信号故障诊断的流程图Figure 4 Flow chart of fault diagnosis for non-stationary vibration sign

3．1 小波变换

小波变换是在傅里叶变换的基础上研究的一种新的信号处理方法[17，18]，其利用小波基函数的可伸缩特性，弥补了短时傅里叶变换窗函数固定带来的时频域局限性问题。小波变换具有良好的分辨率，适于非平稳性信号的分析；但对于高频信号，在去噪效果上并不理想，需要在此基础上进一步优化。许多学者在小波变换的基础上进行改进，提出了小波包、小波阈值降噪等方法。文献[19]在小波变换的基础上提出一种改进的小波阈值函数算法，经过仿真与实例验证，证明其可以提高信号的信噪比提高均方误差，具有一定的去噪效果。文献[20]根据小波变换与灰度矩理论建立了一种水电机组振动区方法，并以实际电站的机组数据根据灰度矩建立了机组振动区，随着振动信号的增强，灰度矩数据也会逐渐增大，从而进行振动强度的判别，实现振动分析。文献[21]利用小波包对振动信号进行分解，在利用样本熵对分解信号进行特征提取，最后用学习向量量化神经网络验证具有良好的识别率，此方法可为小波变换方法提供一定借鉴。

3．2 变分模态分解

变分模态分解（VMD）[22]通过迭代搜寻变分模型，将由多成分组成的信号分解成数个有限带宽的固有模态，避免了模态混叠问题。变分模态分解中关于模态个数K和惩罚因子a的选择至关重要，不合适的参数会造成欠分解或过分解的现象[23]。文献[24]以合成峭度倒数与信息熵的乘积最小为目标，对分解的模态分量进行计算得到最优模态，并将特征向量输入到经PSO优化的向量机里进行故障诊断取得良好去噪及诊断效果。文献[25]提出一种改进的PSO优化VMD参数，再通过相关系数阈值法选择最优模态函数，再利用奇异值法进行二次去噪并与其他方法进行对比，证明此方法去噪效果更佳，具有一定的对比价值。文献[26]利用皮尔逊相关系数确定VMD参数，同时计算各阶分量熵值，形成特征分量再输入到经萤火虫优化的概率神经网络中进行故障识别，可以实现微弱故障特征提取及故障诊断，但分离信号和噪声的效果不够理想，需要进一步研究。

3．3 奇异值分解

奇异值分解利用测量信号构建矩阵，根据矩阵分解的奇异值来反映信号与噪声情况，将代表噪声信号的奇异值归零实现噪声的去除，奇异值分解关键在于确定有效秩的阶次和重构矩阵的结构[27]。文献[28]将小波变换与奇异值相结合来提取水电机组的振动特征实现故障诊断，在二次去噪的基础上将得到的奇异值作为特征向量输入到概率神经网络中进行识别，此法便捷、灵活、为机组故障诊断提供一定依据。文献[29]采用傅里叶分解与奇异值联合降噪，在傅里叶分解的基础上利用奇异值差分谱确定降噪阶次，实现最大程度上的降噪，并在包络谱分析中能够有效提取滚动轴承故障特征。

3．4 贝叶斯网络

贝叶斯网络是概率图模型中的一种，主要是用来描述随机变量之间的条件依赖，研究系统中涉及的随机变量形成贝叶斯网络。其主要用于解决不确定性问题概率推理方法中事件先验概率确定困难和多变量联合概率密度缺乏有效推理算法的问题[30]。在文献[31]中，贝叶斯网络的结构与节点由专家经验及EM算法学习获得。将经SOM神经网络处理后的离散数据输入到已搭建完整的贝叶斯网络模型，再经推理验证可得到故障发生的后检概率，为后续机组状态检修提供一定依据。

3．5 支持向量机

支持向量机是由 Vapnik[32]提出，其核心思想在于找到一个最优分类面使支持向量到最优分类面的距离最小，在样本数据分析与模式识别等方面具有突出优势。但支持向量机仅限于小样本处理，在样本参数不合适或样本量较大时会产生效率低下的疲劳学习后果。在此基础上，一些基于支持向量机的改进算法，如最小二乘支持向量机等，得到了研究与应用，提高了传统方法的求解速度。文献[33]利用粗糙集将数据进行简化处理，减少了样本冗余度提高了向量机的故障诊断效率，在输电系统诊断中取得了良好诊断效果。文献[34]用VMD将轴承故障信号进行处理将得到的频谱特征输入到经粒子群算法优化过的最小二乘支持向量机里得到故障模式分类确诊精度。

4 总结与展望

本文针对常规水电机组与接入风光电的水电机组振动进行分析，在总结已有研究的基础上，从非平稳性振动信号出发，针对已有的时频域信号处理方法与故障诊断方法进行综述。但目前仍有许多关键问题还没有得到妥善解决，未来可以从以下几个方面进行考虑：

（1）微弱故障特征的提取：在强噪声背景的干扰下，反映机组故障特征的有效信息较为微弱需要不断深入研究。

（2）复合故障振动分析：考虑到水力机组振动的复杂性，机组发生振动时往往不会是单一部位，考虑多个部位复合振动分析与故障识别存在难度，未来需要重点关注以解决水电站实际应用难题。

（3）健康评估等预测技术：预测故障发展趋势可以对机组异常状态做出防范，采取相应措施进行管控。考虑到机组故障数据有限，目前关于机组健康评估都是基于健康数据挖掘关键信息，联合机组多变工况建立评估模型是未来发展之一。

（4）接入风光电的水电调节问题：水电在水—风—光互补系统中启停频繁，考虑到振动区运行危害机组安全稳定性，需要减少振动影响加大机组稳定运行区间。