矩形钢管H型蜂窝柱特征值屈曲分析在ABAQUS中的应用

岳春龙

(黑龙江省交通运输信息和科学研究中心，黑龙江 哈尔滨 150080)

1 引 言

本文基于截面形状为矩形的钢管混凝土结构翼缘的H型蜂窝组合柱应用有限元软件ABAQUS进行仿真屈曲分析，然后与之相关的理论数据进行对比分析，进而来验证模型建立的正确与否，最终得到最适合在ABAQUS软件中计算该类型结构的组合柱模型和网格的尺寸大小。

2 ABAQUS有限元软件的简单介绍

ABAQUS[1]公司的前身是由Karlsson，Sorensen和Hibbitt博士成立的HKS。ABAQUS是一款具有强大分析功能的有限元软件，它可以解决十分广泛的问题，既能分析简单的线性问题，也能分析较为复杂的非线性问题，例如从特征值屈曲分析到带有初始缺陷的非线性屈曲分析，ABAQUS有限元分析软件它具有一套标准化的准则以及快速分析的机制，能在最大程度上实现分析得出的结果与实际情况基本保持一致，并且将误差降低到最小。

3 相关理论

3.1 柱的挠曲函数

根据柱顶的约束条件及杆脚受力的约束条件进行综合的考虑。本文研究长度为L的柱子，柱顶采用可动铰接，柱底采用固定铰接。我们建立如下坐标系，取坐标原点在柱脚，y方向表示竖直向上的方向，x方向表示水平向右的方向。竖直向下的荷载P作用在柱子的顶部。

当使用中性平衡法[2]来计算构件的屈曲荷载时，我们可以选取隔离体，离底端x距离处的挠度为y，作用于截面的弯矩为Me=Py，内力矩为截面的抵抗力矩[3]Mi=ELΦ=-EIy″,此时平衡方程为外弯矩等于抵抗力矩，即Mi=Me，即式(1)

Ely″+Py=0

(1)

式(1)中E为材料力学中的弹性模量；I为截面惯性矩。引用符号m2=P/EI，将转换为常系数微分方程(2)

y″+m2y=0

(2)

利用高等数学方法，求解常系数微分方程，得到其通解的表达式

y=Csinmx+Dcosmx

(3)

未知系数C、D和待定值m，且有两个相互独立的边界条件，即y(0)=0和u(l)0带入上式(3)后得到D=0和下式(4)

Csinml=0

(4)

满足式(4)的解有一般有两个，一个是C=0，即表明构件仍然是垂直状态，不满足构件处在微弯状态的意义，所以只有非平凡解。因为C10，所以

sinml=0

(5)

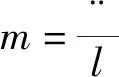
图1 试件的横截面类型及具体尺寸(单位/mm)

(6)

式中:C为未知常数。

4 材料本构模型选取

钢材本构关系通过应力-应变曲线描述钢材的力学性能[2]，根据钢材不同的型号和研究类型选取合适的本构关系极其重要。标准钢材的应力-应变曲线主要包括弹性阶段、弹塑性阶段、屈服阶段、强化阶段以及颈缩阶段五个阶段。在本文中，主要研究基于矩形钢管混凝土结构翼缘的H型蜂窝组合柱的特征值屈曲分析，此过程主要研究钢构件弹性阶段，所以将应力-应变曲线简化为理想的弹塑性模型。

5 有限元模型建立分析及验证

为验证有限元模型建立的可靠性，本文根据普通型钢材和H型钢材的相关规范[4]，以约束方式、截面形式、构件长度和混凝土强度等级为参数，设计了11根H型钢柱，在保证单一变量的情况下对11组构件进行分析，在11根钢柱中，对8根翼缘矩形钢管中布置竖向加劲肋。 B-1是常规的H型蜂窝钢柱；B-2、B-3截面面积与B-1相同；试件B-4-B-7柱H型柱截面面积与B-1钢柱截面面积相同同时增加四种不同形式的加劲肋； B-8-B-11通过减小柱的腹板厚度或着翼缘厚度的手段，来相对于转化为加劲肋；试件主要参数和设计原则如表1所示，表中A-1表示试件约束方式为上端铰接及下端固接的约束方式。根据规范《钢结构设计规范》[4]，能够确定试件的计算长度系数。

表1 试件主要参数与设计原则

本章主要研究翼缘为钢管的H型蜂窝钢柱，本章试件的约束方式均采用A-1即上端铰接下端固接的约束方式。

跟据《钢结构设计规范》，能够确定试件的计算长度系数。图1为试件的11种不同形状的截面形式。三种不同截面形式的试件三维图如图2所示。

图2 三种截面形式的试件立体图

6 不同网格尺寸下屈曲荷载对比

本文的模型是高度为10 m的H型钢柱，对四种不同典型的截面形式的H型钢柱选择用不同的网格尺寸来进行特征值屈曲分析，分析在不同的网格尺寸下，相同截面的屈曲荷载随着长细比的变化而变化的规律，同时绘制对应的变化曲线，对比曲线如图3所示。

通过分析上述不同网格尺寸划分时的四种不同的截面形式的试件及不同长细比的构件在不同网格尺寸情况下的屈曲荷载，并与屈曲荷载理论解进行对比，由图3能够得出结论：当网格的尺寸为0.16的时候，屈曲荷载有限元分析的数值解和理论解相比较相差最大；网格的尺寸为0.12的时侯，试件屈曲荷载数值解与理论解吻合相对较差；当网格的尺寸为0.08时，试件屈曲荷载数值解与理论解吻合相对较好；当网格的尺寸为0.04 m的时候，四种不同的截面形式的构件屈曲荷载有限元分析的数值解曲线与屈曲荷载理论解的曲线吻合相对来说是最好。由此可以得出结论：网格划分越细化，通过有限元分析模型，所得出的结果也会更加的合理精确。综上所述，本文将采用网格尺寸为0.04 m作为部件的网格划分结果。

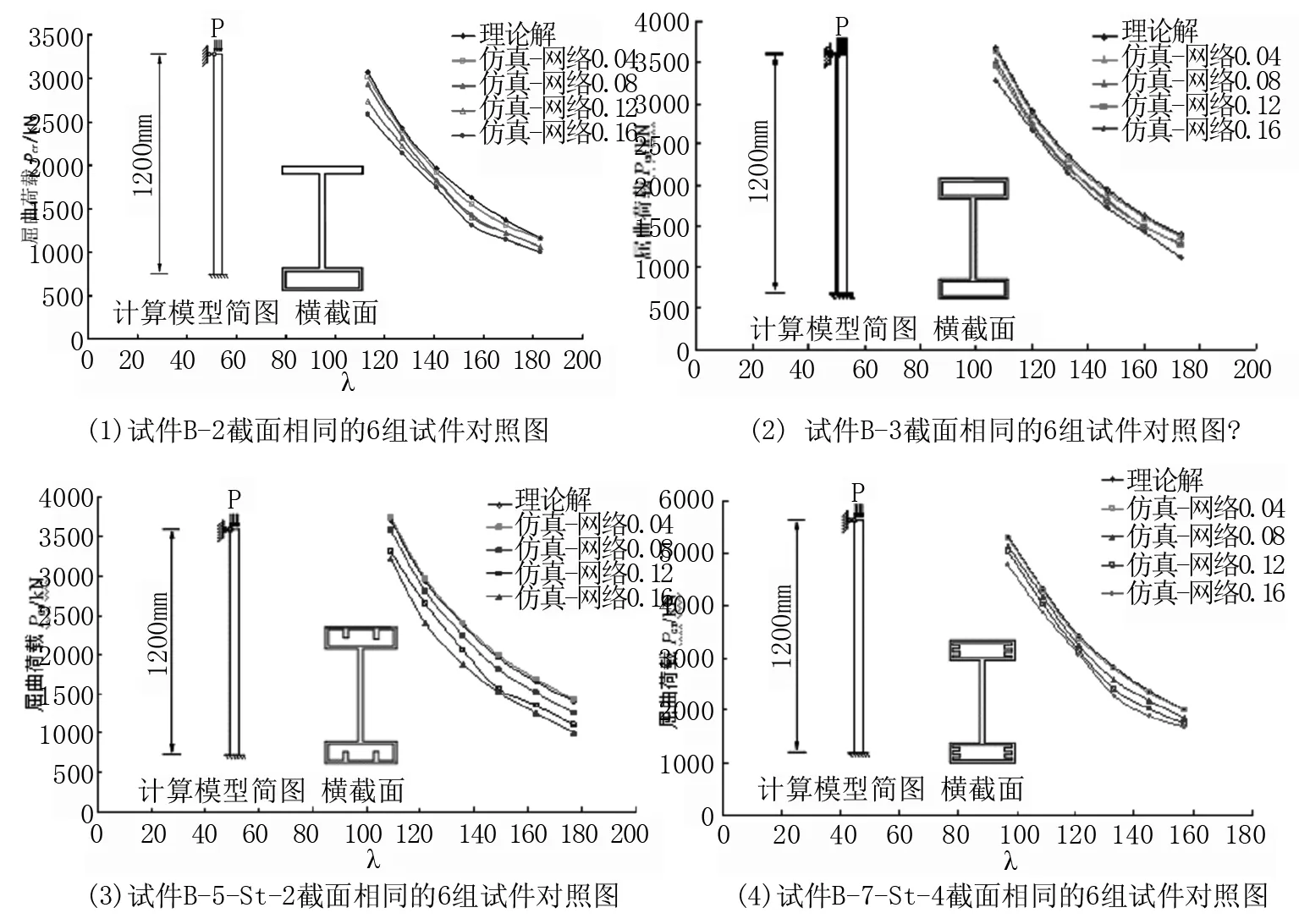
图3 有限元分析的数值解和理论解的相互对比

7 结 语

本章节以实际长度、约束方式、截面形式、加劲肋类型为变量，设置多组试件在多种网格尺寸的情况下利用ABAQUS有限元软件开展钢柱的特征值屈曲分析，通过分析得到以下结论。

(1)在进行钢柱的特征值屈曲分析时，ABAQUS中划分网格尺寸建议取值0.04 m，若网格尺寸过大将导致仿真结果不准确，若网格尺寸过小将导致运算过于缓慢。

(2)对于本文类似结构的仿真分析，用理想的钢材本构模型便可进行相应的数值模拟分析，仿真结果与理论结果相差较小。

(3)通过稳定性理论公式求解屈曲荷载，并与数值仿真解对比，便可说明本文建模方法和本构关系选取的正确性。

(4)本文将普通H型钢柱钢板翼缘做成矩形钢管的形式并添加加劲肋，网格尺寸划分为0.04 m，并按照规范规定进行特征值屈曲分析，其屈曲荷载得到明显提高。