基于固定时间的柔性关节空间机器人阻抗控制
2022-09-08刘辽雪洪梦情顾秀涛高俊彦
刘辽雪,洪梦情,顾秀涛,高俊彦,郭 毓
(南京理工大学 自动化学院,江苏 南京 210094)
目前我国空间技术不断发展,航天需求也与日俱增。大型空间站组装、检测与维护,故障航天器的回收与维修等,都对空间在轨服务机器人提出了更新更高的要求,柔性关节空间机器人在其中更是扮演了关键角色[1]。然而,以上空间任务操作过程中均需要空间机器人与环境接触,仅进行位置控制难以实现更高控制精度的需求。因此,兼顾力控制的柔顺控制方法受到越来越多的国内外学者的关注[2,3]。
阻抗控制作为一种主动柔顺控制方法,常用来实现位置与力的控制,自提出以来,受到了广泛关注[4]。Li等[5]针对由串联弹性执行器驱动的康复机器人阻抗控制问题,结合康复机器人的任务特点,提出了一种基于迭代学习的控制方法,有效解决了重复工作情况下的阻抗控制问题。Brahmi等[6]针对外骨骼康复机器人,考虑人类肌肉骨骼状况,提出了一种基于非线性时滞干扰观测器的自适应阻抗控制方法,对系统模型不确定性以及外部干扰提供了准确的补偿。Jiang等[7]提出了一种适用于柔性关节机械臂的阻抗控制方法,并通过末端带有力传感器的两连杆柔性关节机械臂验证了所提方法的有效性。熊根良等[8]也针对柔性关节机械臂的柔顺控制问题,设计了一种基于反演法的阻抗控制器,实现了柔性关节机械臂末端与环境之间的柔顺接触。相比于地面机器人,空间机器人需要考虑基座与机械臂之间的耦合作用,其姿态运动极易引起基座姿态持续振动和机械臂末端颤振[9],这对柔性关节空间机器人的阻抗控制器设计带来了更大的挑战。不仅如此,上述研究成果仅能保证系统状态渐进收敛到平衡点,不适用于一些对快速性有较高要求的空间任务。
固定时间稳定相比于有限时间稳定,其收敛时间上界不依赖于系统的初始状态,更适用于实际应用。Zou等[10]针对刚性航天器跟踪控制问题,基于反演法与“功率积分器”思想,提出了一种新型的固定时间控制律,保证了姿态跟踪误差在固定时间内收敛到原点。He等[11]针对柔性连杆机械臂的振动控制问题,基于神经网络提出了一种固定时间的学习控制方法,实现了误差的快速收敛。陈明等[12]针对一类严格反馈非线性系统,基于反演法设计了固定时间跟踪控制器。但是以上研究没有考虑反演法的虚拟控制律求导导致的“复杂度爆炸”问题,不利于实际工程应用。针对虚拟控制律求导“复杂度爆炸”问题,文献[13-15]使用非线性滤波器代替传统动态面方法中的一阶滤波器,在保证系统固定时间收敛的同时有效地解决了这一问题。其中,Ni等[13]针对三总线电力系统中的混沌振荡抑制与电压稳定问题,提出了一种固定时间动态面高阶滑模控制器,并给出了半全局固定时间最终一致有界稳定的定义,具有重要的理论和实际意义。
本文针对一类外部干扰影响下的自由飞行柔性关节空间机器人,基于反演法设计了一种固定时间收敛的阻抗控制器,使之在无环境障碍条件下能够快速实现末端执行器位置高精度跟踪控制,在有环境障碍的情况下快速实现柔顺控制。
1 问题描述与预备知识
1.1 系统动力学模型
对于一类自由飞行即基座姿态受控的柔性关节空间机器人,考虑所装配的机械臂为2关节的情形,在平动惯性坐标系中使用拉格朗日法所建立的动力学模型如式(1)所示[9,16]

(1)

(2)
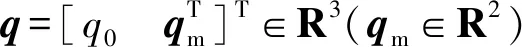

(3)
式中:d=M-1(x1)τd,Kb=diag(1,k1,k2),a1=diag(0,1,1),a2=[0I2]T(I2为2阶单位矩阵),a3=[1 0 0]T。
假设1状态量xi(i=1,2,3,4)可以通过测量获得。
假设2外部干扰力矩是有界的,又因为空间机器人惯量矩阵有界,故增广误差d满足‖d‖ 所谓期望阻抗模型是描述柔性关节空间机器人在与外部环境接触时期望表现出的动力学行为。通常使用如下所示的质量块-阻尼-弹簧系统来等效[5] (4) 式中:Md=diag(Md1,Md2,Md3)、Cd=diag(Cd1,Cd2,Cd3)、Kd=diag(Kd1,Kd2,Kd3)∈R3×3分别表示期望惯量矩阵、期望阻尼矩阵和期望刚度矩阵。 定义基座和关节转角误差e1=x1-yd以及辅助变换矩阵如下 (5) (6) (7) 式中:Λ和Γ均是正定对角矩阵。式(7)可以通过一个低通滤波器实现,滤波器的输入为τe,输出为τa。 (8) 控制目标:针对式(3)所示的自由飞行柔性关节空间机器人系统,设计合适的控制律τ,使系统在外部扰动下,能够让阻抗误差中间向量在固定时间内收敛到0的任一小邻域内。即 ‖z‖→εt≥T (9) 式中:ε为正常数,T是一个仅与控制系统参数相关的有界函数。 定义1[13]考虑系统 (10) 式中:x(t)∈Rn是系统状态变量,f(·)表示非线性函数。若存在: (1)与初始状态x0无关的有界函数T:Rn|R+; (2)紧集W0⊂Rn与任意小紧集W⊂Rn。 对于任何从集合W0出发的状态轨迹x(t),都能在有限时间tf内进入集合W,且tf≤T。即 (11) 则式(10)系统中的状态变量是半全局固定时间一致最终有界的。 引理1[13]考虑系统(10),若存在连续可微正定函数V(x),任意小正实数ζ,以及正实数a,b,α∈(1,+∞),β∈(0,1),当x0∈W0时,有 (12) 则式(10)系统是半全局固定时间一致最终有界的,x(t)可以在固定时间内收敛到平衡点的任意小邻域内。即V(x)≤2γ,a|γ|αsign(γ)+b|γ|βsign(γ)=ζ,其中sign(·)表示符号函数。且收敛时间满足 (13) 引理2[14]对于xi∈R(i=1,2,…,n)及m>0,如下关系式成立 (14) 引理3[14]对于x∈R,α∈(1,+∞),β∈(0,1)及k1,k2,k3>0,如下关系式成立 -k1|x|α-k2|x|β+k3|x|≤-(k1-k3)|x|α- (k2-k3)|x|β (15) 在控制律设计之前,为了简化表达,对于x=[x1x2…xn]T∈Rn及α≥0,定义|x|α=[|x1|α|x2|α… |xn|α]T,sigα(x)=[|x1|αsign(x1) |x2|αsign(x2) … |xn|αsign(xn)]T。 定义基座和关节转角的参考速度和参考加速度为 (16) 于是,可以将阻抗误差中间向量z重新表示为 (17) 定义误差面如下 (18) 式中:ω1,ω2∈R2为非线性滤波器的输出值。 基于动态面方法所设计的非线性滤波器如式(19)所示 ωi(0)=xi+2,d(0)i=1,2 (19) 式中:α∈(1,+∞),β∈(0,1),σj为时间常数,xi+2,d为虚拟控制律。于是,非线性滤波器误差可以表示为 yi=ωi-xi+2,d (20) 对误差yi求导,得到 (21) 选取Lyapunov函数 (22) 对时间求导,结合杨氏不等式与引理2和引理3可得 (23) 本文采用反演方法进行控制器设计,步骤如下: 步骤1对误差s1求导,得到 M-1(x1)(Kba2(s2+y1+x3,d)+Kba3τ0- (24) 设计虚拟控制律x3,d与实际控制律τ0为 (25) 式中: (26) 步骤2对误差s2求导,得到 (27) 设计虚拟控制律x4,d为 (28) 步骤3对误差s3求导,得到 (29) 设计实际控制律τm为 (30) 定理1考虑存在外部干扰的自由飞行柔性关节空间机器人(3),由期望阻抗模型(4)、非线性滤波器(19)以及控制律(25)、(26)、(28)、(30)所组成的控制器,在假设1~3成立的情况下,能够使空间机器人的阻抗误差中间向量在固定时间内收敛到零点的任意小邻域内。 证明选取Lyapunov函数 (31) 对V进行求导,并将式(23)~(30)代入,利用杨氏不等式,整理得 (32) 根据引理2和引理3对式(32)进行放缩可得 (33) 式中: 对于任意的p>0,集合Π={(s1,s2,s3,y1,y2):V≤p}在R11上为紧集,因此‖ξi‖(i=1,2)在Ω×Π内有最大值Bi,于是 (34) 因此,对于V(0)≤p,设计适当参数λi,μi,σj,α,β(i=1,2,3,j=1,2),使得γ1>0,γ2>0,根据引理1可知系统(3)是半全局固定时间一致最终有界的,阻抗误差中间向量z可以在固定时间T内收敛到零点的任意小邻域内,且收敛时间T满足以下不等式 (35) 定理1得证。 (36) 控制器参数设置如下:λ1=μ1=diag(12,9,8),λ2=μ2=λ3=μ3=diag(3,3),α=1.25,β=0.8,σ1=σ2=0.002,Md=diag(100,100,100),Cd=diag(300,300,300),Kd=diag(200,200,200)。 为验证所提控制方法的有效性,与文献[17]所提反演控制方法进行对比,根据本文被控对象所设计的虚拟控制律与实际控制律如下 (37) (38) (39) 式中:控制器增益设计为K1=λ1,K2=λ2,K3=λ3。 分别针对以下两种情形进行仿真。 仿真Ⅰ:机器人未与环境接触情形下的姿态跟踪控制;仿真Ⅱ:机器人与环境接触情形下的阻抗控制,环境障碍处坐标假设为x=1.2 m,环境参数fe=-Kμμ,其中Kμ为环境刚度,设置为Kμ=diag(500,500),μ为空间机器人与环境接触导致的形变量。 仿真结果如图1和图2所示。 图1 仿真Ⅰ情形下控制算法性能对比 图2 仿真Ⅱ情形下控制算法性能对比 由图1(a)与图2(a)可知,两种算法均能使柔性关节空间机器人系统的阻抗误差收敛到零的邻域内,此时空间机器人的末端执行器能够表现出所设置的期望阻抗模型的动力学行为。但是相较于文献[17]中的方法,本文所提基于固定时间收敛的阻抗控制方法具有更快的收敛时间,阻抗误差可以在1 s左右收敛到零附近,同时本文方法也使阻抗误差具有更快的收敛速度以及更小的波动。从图1(b)、图1(c)可以看出,在没有环境障碍的情况下,系统完成了期望轨迹的高精度跟踪,且相较于对比方法,本文方法能够使跟踪误差在4 s左右收敛到零附近,收敛精度也有较大的提高。但是从图1(d)与图2(d)也可以发现,本文方法存在初始控制力矩较大的缺点,有待进一步研究。从图2(b)、图2(c)可以看出,当存在环境障碍时,阻抗控制方法会根据设置的期望阻抗模型,通过调整跟踪误差使空间机器人的末端执行器顺应外界环境,从而使得空间机器人表现出更好的柔顺控制效果。 本文针对一类自由飞行的柔性关节空间机器人柔顺控制,考虑到外部干扰,结合反演方法提出了一种基于固定时间收敛的阻抗控制器,实现了空间机器人阻抗误差的快速收敛,并有效地抑制了外部干扰的影响,提高了系统的鲁棒性。采用非线性动态面方法简化了控制器设计过程中虚拟控制量的求导运算,同时保证了固定时间稳定条件。仿真结果验证了所设计的控制器能够使自由飞行柔性空关节间机器人以较高的位置跟踪精度、较小的阻抗误差、较快的收敛时间完成柔顺控制任务。
1.2 期望阻抗模型


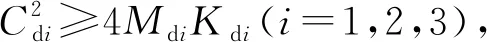




1.3 预备知识
2 固定时间阻抗控制器设计与稳定性分析
2.1 控制器设计
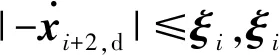
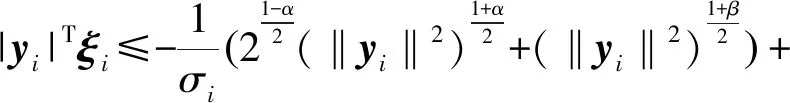

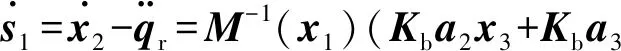



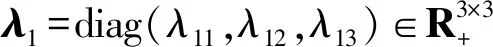
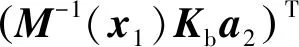

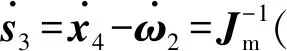
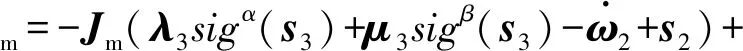
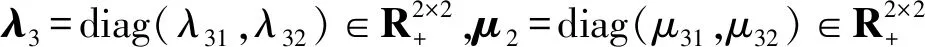
2.2 稳定性分析


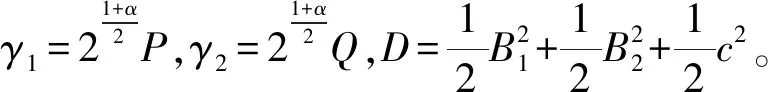
3 仿真验证

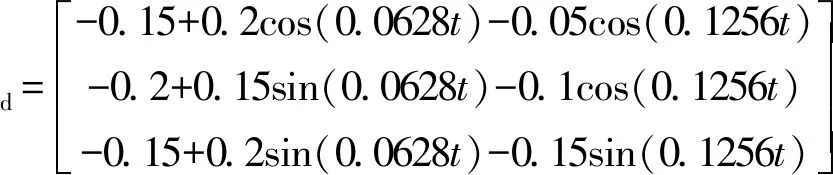
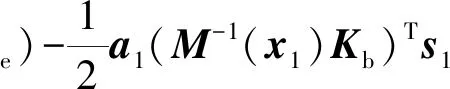
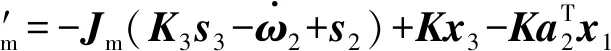


4 结束语
