结构方程模型统计检验力分析：原理与方法*

翟宏堃 李 强 魏晓薇

·研究方法(Research Method)·

结构方程模型统计检验力分析：原理与方法*

翟宏堃 李 强 魏晓薇

(南开大学社会心理学系, 天津 300350)

结构方程模型是心理学、管理学、社会学等学科中重要的统计工具之一。然而, 大量使用结构方程模型的研究忽视了对该方法的统计检验力进行必要的分析和报告, 在一定程度上降低了这些研究的结果的证明效力。结构方程模型的统计检验力分析方法主要有Satorra-Saris法、MacCallum法与Monte Carlo法三类。其中Satorra-Saris法适用于备择模型清晰、检验对象相对简单、检验方法基于χ2分布的情形; MacCallum法适用于基于χ2分布的模型拟合检验且备择模型不明的情形; Monte Carlo法适用于检验对象相对复杂、采用模拟或重抽样方法进行检验的情形。在实际应用中, 研究者应当首先判断检验的目的、方法以及是否有明确的备择模型, 并根据这些信息选择具体的分析方法。

结构方程模型, 统计检验力, 模型拟合检验, 模型参数检验

1 引言

结构方程模型(Structural Equation Model, SEM)是心理学、管理学、社会学等学科中重要的统计工具之一, 可以用于验证性因子分析、共同方法偏差检验、中介/调节效应分析、交叉滞后分析等多种场景。有研究者指出, 相较于一般的回归分析, 结构方程模型能够更好地控制测量误差, 也支持构建复杂的多变量模型(王阳等, 2020)。然而, 在使用结构方程模型进行分析时, 却较少有研究者报告统计检验力的相关内容。事实上, 统计检验力的大小在零假设显著性检验(Null Hypothesis Significance Testing, NHST)中有着重要的参考价值。

统计检验力指的是某假设检验能够正确地拒绝错误零假设的概率。对统计检验力进行分析, 可以帮助研究者确定合理样本量, 避免造成大量的人力和物力的浪费(吴艳, 温忠麟, 2011; 赵礼, 王晖, 2019)。此外, 对评估结构方程模型拟合的χ2检验而言, 零假设的形式通常为模型拟合良好或模型间无差异, 而备择假设则通常为模型拟合不良或模型间存在差异。针对此类假设, Ⅱ类错误意味着研究者可能将拟合不良的模型误认为拟合良好的模型进行结果报告。王阳等人(2020)则指出, 若模型设定有误, 建立在此模型基础上的参数估计结果都是不可靠的。在这种情况下, Ⅱ类错误可能带来比Ⅰ类错误更大的危害。

近年来, 有一些研究者开始逐渐意识到使用结构方程模型作为统计工具时统计检验力分析的重要性, 并开始在研究中报告其先验或后验检验力, 或者至少在讨论部分指出该研究可能在统计检验力上存有不足(Mullen & Crowe, 2017; Hollerbach et al., 2018; Kornadt et al., 2019; Zhang & Zaman, 2020; Zhai et al., 2021)。但值得注意的是, 目前仍有许多研究者在使用结构方程模型时并未提及统计检验力的有关内容。笔者曾以全文包含“结构方程模型”或“SEM模型”为条件, 搜索了国内心理学顶级刊物《心理学报》中近5年(2017～2021)内发表的论文, 共检索出51篇论文, 排除其中6篇方法类研究和2篇元分析研究, 余下43篇中提及“统计检验力”或“统计效力”的仅有2篇研究。本文介绍结构方程模型统计检验力分析的基本原理和具体分析流程, 并进行了实例演示, 最后对相关问题进行了讨论。

2 结构方程模型中的假设检验

假设检验的技术路线直接决定了检验力分析所能选取的技术路线, 结构方程模型中假设检验的技术路线大致可分为两种: 基于χ2分布的方法以及基于模拟(simulation)或重抽样(resampling)技术的方法。

2.1 基于χ2分布的结构方程模型检验

基于χ2分布的结构方程模型检验主要包括用于评价模型拟合(或嵌套模型比较)的χ2检验、Δχ2检验、等效性检验、基于模型拟合指数的检验以及用于评价模型参数(或参数的函数, 如中介效应)的Wald检验、拉格朗日乘子检验(Lagrange Multipliertest, LM检验)和似然比检验(Satorra, 1989; Chou & Bentler, 1990; Gonzalez & Griffin, 2001; Yuan & Chan, 2016; Yuan et al., 2016; 王阳等, 2020)。这些检验涵盖了结构方程模型相关假设检验的方方面面, 甚至可以说, 目前与结构方程模型有关的参数检验方法要么本身就是χ2检验, 要么可以通过适当变形转化为χ2检验。根据构建统计量时的细微差别, 上述检验又可被划分为三个子类。

首先是χ2检验、Δχ2检验、等效性检验和似然比检验, 这四种检验都以结构方程模型的拟合函数为基础。结构方程模型的拟合函数衡量了样本协方差矩阵与假设模型对应的协方差矩阵Σ0之间的差距, 亦即变量间关系在假设模型与实际数据中的差距(吴明隆, 2010; 王阳等, 2020)。Muthén(2004)指出, 当样本来自假设模型所对应的正态总体时, 拟合函数值的倍(为样本量)随着的增大渐近服从中心化χ2分布。另有学者则指出, 当假定样本来自与假设模型差距小于给定值(记作F)的正态总体时, 此时拟合函数值的倍渐进服从非中心参数为()F的非中心χ2分布(Satorra & Saris, 1985; MacCallum et al., 1996; Yuan & Chan, 2016)。据此, 可以构建出零假设成立时χ2检验和等效性检验所对应的统计量分布。而Δχ2检验和似然比检验则是在前者的基础上, 增加了对假设模型的约束条件, 通过比较添加约束条件前后实际数据与假设模型的差距是否显著增大来判定添加的约束条件是否“合理”。

第二类是基于模型拟合指数的检验。从原理上讲, 这类检验与第一类检验差别不大, 其本质是通过拟合指数的定义式将拟合指数换算为非中心参数, 因此该方法仅能用于根据非中心参数定义的拟合指数(如RMSEA、CFI、MFI、GFI1本文中出现的“GFI”和“AGFI”指的分别是“Unbiased goodness of fit index”和“Unbiased adjusted goodness of fit index”, 而非“Goodness of fit index”和“Adjusted goodness of fit index”, 详见网络版补充材料。等)。此类检验有两种相似但略有不同的技术路线, 一种将基于模型拟合指数的零假设换算为基于非中心参数的零假设, 选择非中心参数的临界值作为构建χ2统计量分布的依据, MacCallum等人(1996)和MacCallum等人(2006)就采用了这种做法。另一种则根据Venables (1975)的研究, 以样本计算出的非中心参数估计值为依据构建总体非中心参数的1 − α置信区间, 再根据定义式将其换算回拟合指数, 从而得到拟合指数的1 − α置信区间, 进而完成统计推断。基于CFI与RMSEA的等效性检验则采用了此类做法(Yuan et al., 2016; Marcoulides & Yuan, 2017; 王阳等, 2020)。

第三类是Wald检验和LM检验。与前两类方法不同的是, 此类方法不再关注样本的拟合函数值本身(非中心参数也是关于拟合函数的函数), 而是通过对关键参数及其标准误的估计, 构建z统计量进行检验。其中Wald检验以备择假设成立时的模型为基础完成对目标参数的估计和检验。当处理参数函数形式的假设时, Wald检验对参数函数在其真值邻域内进行一阶Taylor展开求得其线性近似值, 进而完成对待检验指标的标准误估计(Chou & Bentler, 1990; Gonzalez & Griffin, 2001)。此时Wald检验亦称为Delta法, 叶宝娟和温忠麟(2012)曾介绍过如何利用该方法对多维测验合成信度的置信区间进行估计。与Wald检验相对, LM检验以零假设成立时的模型为基础, 将假设条件重写为约束函数的形式, 并构建拉格朗日函数将原假设检验问题变为检验拉格朗日乘数是否为0的问题(Chou & Bentler, 1990)。若拉格朗日乘数为0, 则意味着新假设条件的加入没有改变原假设模型。

2.2 基于模拟或重抽样技术的结构方程模型检验

近年来, 随着计算机技术的发展, 模拟技术和重抽样技术越来越多地出现在统计学领域, 这些技术被广泛地运用在包括参数估计与假设检验在内的多种场合。不同于基于理论分布的经典方法, 此类方法通常以模拟或重抽样的方式得到目标统计量的经验分布, 并以经验分布代替理论分布进行统计推断, 因此往往用于目标统计量的理论分布不明确或难于计算的情形。此类方法中最为重要的两种分别是基于模拟技术的Monte Carlo (MC)方法2Monte Carlo方法实际上代表的是以计算机模拟为核心的一组方法, 为了和后文统计检验力分析的Monte Carlo方法加以区分, 假设检验的Monte Carlo方法本文统一简称为MC方法/MC法, 特此说明。与基于重抽样技术的Bootstrap方法。

MC方法最早由Stanisław Ulam等人于20世纪40年代中期提出, 其核心思想为采用模拟的方式“重现”某一概率模型所描绘的过程, 以模拟得到的结果作为目标问题的近似解。MacKinnon等人(2004)在评估中介效应检验的M法和经验M法时同时引入了MC法。Preacher和Selig (2012)进一步指出MC法不仅可以用于线性回归和路径分析模型, 也可直接扩展至潜变量模型。该方法假定模型参数服从联合正态分布, 其均值向量与协方差矩阵通常由对原始模型的极大似然估计确定。MC法将模型参数视为从确定的联合正态分布中抽样的过程, 以此为基础进行随机抽样, 最终基于抽样结果构建中介效应的经验分布并进行统计推断(Preacher & Selig, 2012)。此外, 在结构方程建模中还有一类Monte Carlo方法——马尔可夫链蒙特卡洛(Markov chain Monte Carlo, MCMC)方法, 此类方法主要用于贝叶斯结构方程建模中。由于对“参数”这一重要概念的基础假设不同, 贝叶斯统计中假设检验和统计检验力分析的过程均与基于频率学派的传统统计学有着较大的区别, 本文的内容仍然在频率学派的框架内, 故对该方法不做过多介绍。

注意到, 基于模拟技术的结构方程模型检验仍然对分布有着较强的假设, MC法假定路径系数服从联合正态分布, 基于贝叶斯统计的MCMC法需要给出模型参数的先验分布与给定参数时样本的条件分布。相比之下, 基于重抽样技术的检验对样本分布的假设更弱, Efron (1979)提出的Bootstrap法3事实上, Bootstrap法还分为参数Bootstrap法和非参数Bootstrap法, 参数Bootstrap法由于需要了解随机变量的分布型态, 在实际中使用不多。本文中若不加说明, Bootstrap法特指非参数Bootstrap法。仅要求样本是从某一确定总体中随机抽样得到的, 对其分布形态并无更多要求。不仅如此, Bootstrap法同样基于“利用经验分布代替理论分布进行统计推断”的思路, 在面对一些理论分布不明或难以计算的场合表现良好。由于Bootstrap法具有前述技术优势, 近年来, 该方法已逐渐成为结构方程模型假设检验问题中的显学, 被广泛应用于多种不同场合。Zhang和Savalei (2016)指出可以用Bootstrap法估计结构方程模型拟合指数的置信区间。Rosseel在其编写的R程序包lavaan中给出了求结构方程模型路径系数的Bootstrap标准误的程序(Rosseel, 2021)。更有研究者利用Bootstrap法估计一些根据结构方程模型路径系数计算得到的更复杂的指标。屠金路等人(2005)利用Bootstrap法对问卷合成信度的置信区间进行了估计; 张涵和康飞(2016)介绍了基于Bootstrap的多重中介效应分析。方杰等人(2011)的研究及温忠麟和叶宝娟(2014a, 2014b)的研究则分别介绍了Bootstrap法在中介效应与有调节的中介效应检验中的应用。

表1中按照不同类别总结了结构方程模型涉及到的常见检验的应用场景、零假设、统计量构建方式、零假设成立时统计量对应的分布以及使用中的优缺点。

3 结构方程模型假设检验统计检验力的分析方法

统计检验力的分析方法与分析对象所采用的技术路径息息相关, 结构方程模型假设检验统计检验力的分析方法也可大致分为两条不同的技术路线: 基于χ2分布的方法和基于模拟的方法。其中, 基于χ2分布的方法可以用于解决使用经典方法进行结构方程模型假设检验时的统计检验力分析问题, 而基于模拟的方法可以用于解决一般的结构方程模型假设检验的统计检验力分析问题。

3.1 基于χ2分布的统计检验力分析

顾名思义, 基于χ2分布的方法以χ2分布的相关理论为基础。此类方法可以追溯到Satorra和Saris早年的一系列研究(Satorra & Saris, 1985; Satorra, 1989; Satorra et al., 1991)。Satorra (1989)指出, 当前述假设检验的H不成立时, 其对应统计量(对Wald检验和LM检验而言是统计量的平方)服从非中心χ2分布, 且其相应的非中心参数可以通过总体协方差矩阵真值拟合零假设模型计算出的统计量得到。进而可以通过计算备择假设成立条件下目标统计量落入拒绝域的概率求得给定检验的统计检验力。设零假设和备择假设成立时对应的非中心参数分别为δ0和δ1, 则统计检验力1 − β由下式给出:

表1 结构方程模型中的假设检验

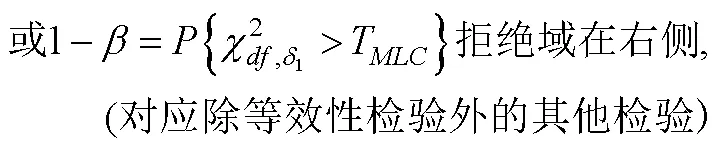
由于δ0在H确定时已经可以算出, 因此, 基于χ2分布的统计检验力分析的关键在于估计δ1。根据估计非中心参数的方法不同, 此类方法又可分为利用总体协方差矩阵Σ进行估计的Satorra- Saris法和利用拟合指数(如RMSEA、CFI、MFI等)进行估计的MacCallum法。

3.1.1 Satorra-Saris法

Satorra-Saris法主要基于Satorra和Saris先前的研究, 其具体步骤如下(Satorra & Saris, 1985; Satorra et al., 1991):

第一步: 定义备择假设成立情况下的模型, 指定备择假设成立情况下的理论总体协方差矩阵Σ。

第二步: 设定样本容量为真实样本容量, 利用Σ拟合零假设模型。

第三步: 将第二步中计算得到的统计量(针对χ2分布的统计量为统计量本身, 针对标准正态分布的统计量为统计量的平方)作为δ1的估计, 代入(1a)或(1b)完成统计检验力计算。

使用Satorra-Saris法估计达到某统计检验力所需样本量的过程与估计统计检验力类似, 只是第二步中需要反复设定样本容量进行多次估计, 并计算不同样本容量对应的统计检验力, 最终从中选取满足目标统计检验力所需的最小样本容量。

Satorra-Saris法通过定义不同于零假设模型的备择模型重构总体协方差矩阵, 并据此计算统计检验力。其中, 对备择模型进行定义的过程不仅需要研究者给出明确的模型结构, 还需要研究者指定大量的参数(如路径系数、测量残差等)。因此, 从应用的角度考虑, Satorra-Saris法更适合在研究者对备择模型的了解程度较深的情况下使用(如针对模型参数的检验)。

3.1.2 MacCallum法

Satorra-Saris法对备择模型过强的假设从客观上提高了该方法的使用难度, 也限制了其适用范围。MacCallum等人(1996)给出了另外一种估计非中心参数的方法, 该方法同样基于Satorra和Saris (1985)给出的公式, 但在估计F时, MacCallum等人给出了一个基于RMSEA的估计方法。他们指出, 使用样本拟合函数估计值F作为对总体参数F的估计是有偏的, 且F与F之间有如下关系(MacCallum et al., 1996):

据此, MacCallum等人提出基于RMSEA指标的统计检验力分析步骤(MacCallum et al., 1996):

第一步: 根据零假设和备择假设成立时对应的RMSEA值、模型自由度以及样本量分别计算出零假设和备择假设成立时的非中心参数δ0和δ1。

第二步: 代入(1a)或(1b)完成统计检验力计算。

与Satorra-Saris法类似, 当使用MacCallum法估计达到某统计检验力所需样本量时, 也只需要在第一步中反复设定不同的对统计检验力进行多次估计, 最终从中选取满足目标统计检验力所需的最小样本容量。

Kim (2005)对MacCallum法进行了进一步简化和扩展, 给出了一个快速求取给定统计检验力情况下所需样本量的公式:

其中为模型自由度, RMSEA为备择假设成立时对应的RMSEA值, δ为显著性水平为α、统计检验力为1−β情况下对应的非中心参数。非中心参数可以通过查表或者使用统计软件计算得到, Kim (2005)在他们的文章最后同时给出了H:F= 0时利用计算机快速求取δ的SPSS与SAS脚本。此外, Kim (2005)在他的文章中还提出了基于CFI、MFI与GFI的计算公式。

相比于Satorra-Saris法, MacCallum法采用拟合指数对模型的拟合情况进行了某种意义上的“打包”, 即利用拟合指数对假设模型与实际数据的差距进行了概括, 使研究者免于设定复杂的备择模型, 在分析模型拟合检验的统计检验力时, MacCallum法仅需要模型自由度、零假设和备择假设成立时对应的拟合指数值[若对关于CFI的检验进行检验力分析时还需要提供基础模型(base model)的拟合函数值F与自由度df, 关于GFI的检验还需要提供协方差矩阵的秩], 大大简化了统计检验力的分析难度。但由于模型参数与拟合指数之间存在复杂的非线性关系, MacCallum法无法分析模型参数检验的统计检验力。

3.2 基于模拟的统计检验力分析

第一步: 根据备择假设成立时的情况设定用于生成模拟数据的均值向量(模型不考虑均值结构时为零向量)与协方差矩阵。此步骤中既可以如Schoemann等人(2017)直接指定协方差矩阵, 也可如Zhang (2014)通过定义模型来间接指定协方差矩阵。此外, 如果研究者希望模拟非正态分布的数据, 通常还需要给出目标分布的峰度和偏度。

第二步: 确定需要进行Monte Carlo模拟的重复轮数与样本容量。Zhang (2014)建议重复轮数通常不应少于1000。

第三步: 在每一轮Monte Carlo模拟中, 重复执行下述步骤: (1)根据给定的分布参数与样本量生成服从特定分布的随机数作为模拟样本; (2)对该模拟样本进行结构方程建模并进行检验, 具体的检验方法可以是表1中的任意一种。

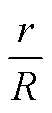
此外, 为了说明Monte Carlo模拟结果的准确性, Muthén和Muthén (2002)建议研究者在报告结果的同时报告结构方程模型中各参数的理论真值、参数估计结果的平均值和标准差、参数估计标准误的平均值以及参数95%置信区间对理论真值的覆盖率。Muthén和Muthén (2002)进一步提出衡量Monte Carlo模拟结果是否可靠的标准: (1)模型中任何参数及其标准误真值与估计值之间的相对误差不超过10% (参数估计结果的标准差视为标准误的真值); (2)模型中关键参数及其标准误真值与估计值之间的相对误差不超过5%; (3)参数的95%置信区间对理论真值的覆盖率应当在0.91至0.98之间。

当使用Monte Carlo法估计达到某统计检验力所需样本量时, 也只需要在第一步中反复设定不同的对统计检验力进行多次估计, 而后通过线性插值法对所需样本量进行估计。与基于χ2分布的统计检验力分析方法相比, 结构方程模型统计检验力的Monte Carlo分析由于不需要计算目标统计量的理论分布, 因此可以广泛适用于对各种检验进行统计检验力分析的情形, 在给出峰度和偏度时, 该方法还可以在一定程度上分析总体分布为非正态分布的情形。但结构方程模型统计检验力分析的Monte Carlo法需要研究者至少给出用以生成模拟数据的协方差矩阵, 这意味着研究者需要对备择假设成立下数据的分布情况有足够的认识。另外, 该方法本身对研究者的编程水平要求较高, 且计算量较大, 计算起来较为耗时, 在一定程度上影响了该方法的使用和推广。

3.3 结构方程模型统计检验力分析的程序资源

为了方便研究者对统计检验力进行分析, 多名研究者提供了在线或离线的相关程序。基于χ2分布的统计检验力分析方法中, Preacher和Coffman (2006)提供了一个基于MacCallum法的统计检验力在线计算程序, 可以计算给定样本量情况下, 单个模型拟合或嵌套模型拟合差异的统计效力或达到某统计效力所需的样本量。Moshagen提供了一个R程序包semPower, 该程序包基于Moshagen和Erdfelder (2016)的研究, 可以计算基于F、RMSEA、McDonald拟合指数、GFI与AGFI的统计检验力, 当指定零假设和备择假设成立情况下对应的协方差矩阵时, 该程序包也可使用Satorra- Saris法分析统计检验力。Jak等人(2021)给出了一个基于Shiny开发的在线程序power4SEM (网址为https://sjak.shinyapps.io/power4SEM/), 该程序同时支持Satorra-Saris法和MacCallum法, Jak等人在他们的论文中详细介绍了该程序的使用方式。

基于模拟的统计检验力分析方法中, Muthén和Muthén (2002)提供了使用Monte Carlo法分析结构方程模型统计检验力的Mplus程序框架。Zhang和Wang (2020)提供了可以用来分析中介效应统计检验力的R语言程序包bmem。该程序包使用Monte Carlo法进行统计检验力分析, 可以对中介效应的Sobel检验与Bootstrap检验的统计检验力进行分析。特别的是, 该程序包还提供给研究者自主设定分布的峰度与偏度的功能以模拟总体为非正态分布时的情形。Schoemann等人(2017)给出了一个使用Monte Carlo法分析中介效应统计检验力的在线程序(网址为https://schoemanna. shinyapps.io/mc_power_med/), 该程序基于Shiny开发, 可用来处理简单中介模型、两个中介变量的平行中介模型和两个中介变量的链式中介模型三种情况下的中介效应统计检验力分析。Wang和Rhemtulla (2021)则给出了一个分析结构方程模型参数检验统计检验力的在线程序(网址为: https:// yilinandrewang.shinyapps.io/pwrSEM/)。

表2中总结了结构方程模型统计检验力分析方法的适用场合、需要的计算量以及相应的程序资源。

4 应用实例

下面用一个例子演示在实际研究中如何灵活使用各种方法对结构方程模型的统计检验力进行分析。注意到, 统计检验力的分析包括先验分析和后验分析, 二者对应研究过程中的不同时期, 且不能相互替代(吴艳, 温忠麟, 2011; 赵礼, 王晖, 2019)。但先验分析与后验分析在分析步骤上差异不大, 且亦有研究者指出, 在NHST中, 统计检验力是值的函数, 在已知值的情况下统计检验力没有给出额外信息, 因此建议无需进行后验分析(Hoenig & Heisey, 2001)。考虑到篇幅所限, 本文仅展示先验分析的过程, 后验分析的部分参见网络版补充材料。演示的样例来自Zhai等人(2021)的研究, 该研究调查了新冠疫情期间个体的心理健康与创伤后成长的基本情况, 并讨论了在控制疫情相关压力和年龄的情况下, 情绪创造力对个体心理健康的保护作用以及对个体创伤后成长的促进作用和可能的作用机制。具体的模型设置参见图1, 统计软件采用R 3.6.3的lavaan程序包和semPower程序包, 本部分全部R代码参见网络版补充材料部分。

从检验目的的角度出发, 使用结构方程模型进行验证性因子分析的主要目的是通过对模型拟合的评价考察样本数据是否符合量表的理论结构, 即考察量表题项与测量因子间的关系是否同研究者的假设所一致; 而使用结构方程模型进行中介效应分析, 特别是对显变量链式中介模型进行中介效应分析时, 研究者的目的则更多指向对路径系数函数(即中介效应)的分析与检验。此外, 注意到图1中的模型为饱和模型, 有研究者指出, 此时模型为完美拟合, 可不关注模型拟合指数, 仅讨论路径系数即可(张莉等, 2019)。综合考虑检验目的与实际情况, 对该研究的统计检验力进行分析时, 需要对验证性因子分析部分模型拟合检验的统计检验力与链式中介模型部分模型参数检验的统计检验力进行分析, 链式中介效应部分选择“情绪创造力→领悟社会支持→情绪调节自我效能感→压力后成长”路径的中介效应值为分析对象。

表2 结构方程模型统计检验力分析方法

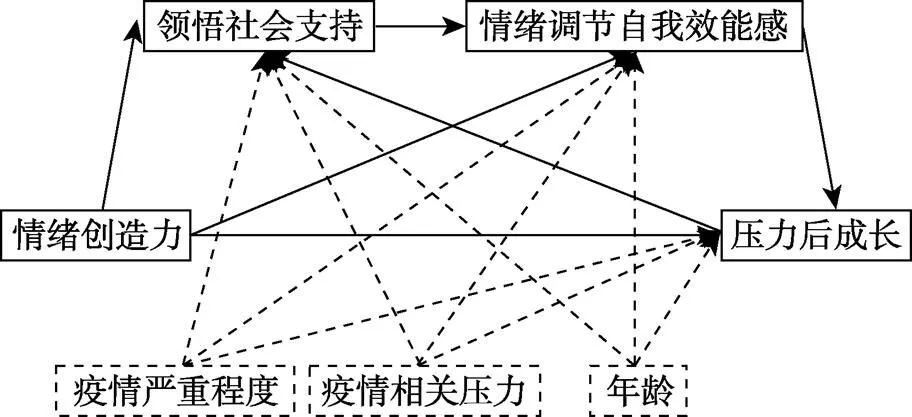
图1 样例的结构方程模型示意图(虚线表示该变量为控制变量)

4.1 模型拟合检验的先验检验力分析

4.1.1 使用Satorra-Saris法分析模型拟合检验的先验检验力

在进行先验检验力分析时, 首先要设定研究对象理论上的总体协方差矩阵(下简称理论协方差矩阵), 即备择假设成立时对应的协方差矩阵。与检验、方差分析的先验检验力分析类似, 在结构方程模型相关检验的先验检验力分析中, 理论协方差矩阵也可以通过参考前期理论、已发表的类似成果或研究者提出的标准所确定(吴艳, 温忠麟, 2011)。通常情况下, 建议研究者优先参考已有类似研究中报告的结果设定理论协方差矩阵, 当缺乏既往研究或既往研究信息不充足时, 研究者可以参考前期理论或其他研究者提出的标准所确定。此外, Jak等人(2021)建议研究者在设定理论协方差矩阵时, 可以以标准化的形式指定参数值, 并且参考相关研究领域中“小、中、大”所对应的经验值代入待定参数。同时, 由于通常情况下确定协方差矩阵所需要的参数数量较为庞大, Jak等人(2021)还建议研究者在设定理论协方差矩阵时需要考虑那些在理论上能够影响拒绝或接受H的重要参数, 例如路径系数、误差相关、潜变量相关等。

通过查询资料发现: 既往研究中, 文书锋等人(2009)的研究较为全面地报告了可以用于生成理论协方差矩阵的全部参数, 且该研究样本量较大(验证性因子分析部分= 818)。因此, 在之后的分析中, 以该模型为基准生成理论协方差矩阵。本例中控制Ⅰ类错误水平α为0.05, 求得统计检验力为0.95时对应的样本量约为134人。此外, 对不熟悉R的研究者, 也可以使用常用的结构方程建模软件(如LISREL、EQS、AMOS、Mplus等)结合G*Power进行分析, 具体的步骤参见网络版补充材料部分。

4.1.2 使用MacCallum法分析模型拟合检验的先验检验力

相比Satorra-Saris法, 使用MacCallum法分析模型拟合检验先验检验力的过程要简单许多, 只需要确定零假设和备择假设成立情况下对应的拟合指数、模型自由度、显著性水平α和统计检验力1 − β五个指标即可完成分析。在设定备择假设对应的拟合指数时, 研究者可参考既往研究中提出的关于该指数“大小”的标准。例如对RMSEA而言, 有研究者指出, RMSEA小于0.05为良好拟合, 0.05至0.08为合理拟合, 0.08至0.1为可接受的拟合, 大于0.1为拟合较差(MacCallum et al., 1996; Yuan & Chan, 2016; Jak et al., 2021)。对于本文中给出的例子, 控制Ⅰ类错误水平α为0.05, 若研究者若希望在RMSEA的真值为0.08时, 正确拒绝该模型的几率不小于95%, 此时使用semPower包提供的semPower.aPriori函数可以计算得出需要的样本量为134人。

4.1.3 使用Monte Carlo法分析模型拟合检验的先验检验力

使用Monte Carlo法分析模型拟合检验先验检验力时确定理论协方差矩阵的步骤和原则同Satorra-Saris法一致, 这里不再赘述。本例中, 以等效性检验为分析对象, 控制Ⅰ类错误水平α为0.05, 重复次数为1000。分别取为101, 201, 301的情形, 计算在给定的情况下1000次重复试验中模型拟合指数落在以RMSEA0= 0.08为经验临界值的等效性检验拒绝域的比率。需要注意的是, 在Monte Carlo模拟的过程中, 有些样本会导致结构方程模型在计算过程中出现迭代不收敛、残差方差为负数、潜变量协方差矩阵非正定等“不合理”的情况, 即出现了不恰当解, 这些解应在在后续的计算过程中予以排除。本例中,分别为101和201时对应的恰当解比例分别为99.6%和100%, 对应的统计检验力分别为0.724和0.996; 对应的各参数估计情况、相对误差以及95%置信区间覆盖率参见网络版补充材料。本例中全部参数均值和标准误的估计误差均不超过10%, 95%置信区间覆盖率均处于0.91至0.98之间, 提示Monte Carlo模拟结果的可信度较高。进一步根据线性插值法可求得统计检验力为0.95时对应的样本量约为185人。针对同一个假设检验进行统计检验力分析时, Monte Carlo方法得到的结果看似与Satorra-Saris法有较大差异, 但这主要是由于线性插值带来的误差。事实上, 若通过缩减采样点间距的方式提高线性插值的精度, 可重新求得待估样本量约为151人。

4.2 模型参数检验的先验检验力分析

4.2.1 使用Satorra-Saris法分析模型参数检验的先验检验力

使用Satorra-Saris法分析模型参数检验先验检验力的第一步仍然是设定理论协方差矩阵。诚然经典的Satorra-Saris法强调通过备择模型生成理论协方差矩阵, 但Satorra和Saris (1985)给出的关于该方法原理的讨论中并没有限制理论协方差矩阵的生成模式。因此, 参照Schoemann等人(2017)的方式直接设定理论协方差矩阵也并无不可。

由于既往研究中缺乏可以用来直接重构理论协方差矩阵的数据, 而通过元分析技术虽然能够在一定程度上基于现有研究构建出理论协方差矩阵, 但这种方法需要耗费较多的人力物力, 单纯用来进行统计检验力分析未免有些浪费。因此, 本文在进行理论协方差矩阵生成时, 选择根据相关研究领域中“小、中、大”所对应的经验值进行设定。此外, 由于尺度变换不影响对本例中所关心的系数(显变量间的路径系数)显著性的判定。因此, 在指定理论协方差矩阵时可进一步将其简化为指定相关矩阵。参考Cohen (1988)的观点, 相关系数在0.1、0.3、0.5时分别对应“小”、“中”、“大”的效应量。在本例中, 假定与控制变量有关的相关系数有“小”的效应量, 关注的变量的相关系数有“中”的效应量, 以此设定理论协方差矩阵。以对“情绪创造力→领悟社会支持→情绪调节自我效能感→压力后成长”这一路径中介效应的Wald检验为分析对象, 控制Ⅰ类错误水平α为0.05, 求得统计检验力为0.95时对应的样本量约为795人。

4.2.2 使用Monte Carlo法分析模型参数检验的先验检验力

本例中, 以对“情绪创造力→领悟社会支持→情绪调节自我效能感→压力后成长”这一路径中介效应的Wald检验为分析对象, 控制Ⅰ类错误水平α为0.05, 分别取为301, 401, 501, 601的情形进行模拟, 得到的结果全部为恰当解, 对应的统计检验力为0.613, 0.884, 0.960, 0.985, 对应的各参数估计情况、相对误差以及95%置信区间覆盖率参见网络版补充材料。本例中全部参数的估计误差均不超过10%, 关键参数的估计误差均不超过5%, 95%置信区间覆盖率均处于0.91至0.98之间, 提示Monte Carlo模拟结果的可信度较高。进一步根据线性插值法求得统计检验力为0.95时对应的样本量约为488人。

5 讨论

5.1 先验检验力分析时的参数设定问题

注意到, 研究者在使用Monte Carlo法或Satorra-Saris法进行先验检验力分析时, 均需要指定理论协方差矩阵。该步骤中, 不论研究者是采用直接设定协方差矩阵的方式还是通过设定理论模型进而生成协方差矩阵的方式, 都需要设定大量参数, 这些参数的设定会对结果产生一定影响, 且影响规律较为复杂。例如, 有研究要对一个两维度, 每个维度包含4个题目的量表进行验证性因子分析。假设H为两维度间不存在相关,H成立的情况下两维度之间存在相关系数为0.3的正相关, 进行先验检验力分析时, 当研究者设定载荷为0.7、0.75、0.8时, 设定显著性水平为0.05, 统计检验力为0.95, 使用Satorra-Saris法计算得到的计划样本量分别为527人、472人和429人, 使用Monte Carlo法计算得到的计划样本量分别为521人、464人和417人。又如, 本文4.2部分给出的例子中, 若将所有控制变量与其他变量的相关系数从0.2变为0.1, 在其他条件不变的情况下, 使用Satorra-Saris法计算得到的计划样本量为352人, 使用Monte Carlo法计算得到的计划样本量为233人。而当分析对象是中介效应或有调节的中介效应这类由参数函数(通常是乘积)构建的指标时, 若研究者使用理论模型生成协方差矩阵, 即使是同样大小的指标值, 不同的参数也会导致分析结果的不同。例如, 对简单中介效应模型而言, 设定自变量到因变量的路径系数为0.2, 中介效应值为0.16, 显著性水平为0.05, 统计检验力为0.90, 中介前半路径系数(自变量到中介变量的路径系数)和中介后半路径系数(中介变量到因变量的路径系数)分别取0.2和0.8, 0.4和0.4, 0.8和0.2(所有系数均为标准化系数)的情况下, 使用Satorra-Saris法计算得到的计划样本量分别为258人、114人和632人, 使用Monte Carlo法计算得到的计划样本量分别为255人、88人和620人。从上述例子中不难看出先验检验力分析中参数设定对结果的影响。这意味着, 研究者在使用Satorra-Saris法或Monte Carlo法进行先验检验力分析时, 应当审慎确定参数的大小, 必要时, 在缺乏既往研究或理论的支持下, 研究者可以反复设定参数的值, 并从结果中选取一个较保守的样本量。

5.2 理论协方差矩阵的产生方式

如前所述, 结构方程模型统计检验力分析的Monte Carlo法和Satorra-Saris法在分析时需要指定理论协方差矩阵, 且理论协方差矩阵的指定存在两种不同模式: 直接指定或通过指定备择模型生成。虽然从分析过程和分析结果上二者可能并无不同之处, 但从逻辑上讲, 不同的理论协方差矩阵生成方式意味着对结构方程建模过程中误差来源的不同理解。Jak等人(2021)指出作为衡量理论模型与真实数据间差异的似然比统计量T实际上包含了两部分的误差: 随机抽样造成的抽样误差和理论模型与真实数据不匹配的误差。事实上, 理论模型与真实数据不匹配的误差还可以再分为两种不同的来源: 来自模型内部参数设定错误以及模型本身对总体的简化。当研究者通过指定备择模型的方式生成理论协方差矩阵时, 研究者实际上默认了模型内部参数设定错误是导致误差的主要来源, 而当研究者通过直接指定的方式生成理论协方差矩阵时, 则将这两种不同来源的误差“打包”在了一起。事实上, 经典的Satorra- Saris法与MacCallum法之间也具有类似的关系, 经典的Satorra-Saris法更加强调来自已经结构化了的模型内部的误差, MacCallum法则通过模型拟合指数将模型内部的误差和模型对总体简化的误差放在一起考察。这种细微的差别意味着研究者需要在面对不同检验的情况下灵活选择理论协方差矩阵的生成方式: 当有较强的理论或既往研究指向误差可能存在于模型内部时, 使用指定备择模型的生成方式; 而当研究者对这些信息掌握程度较少时, 使用直接指定的方式或干脆换用MacCallum法进行分析。

此外, 另一个有趣的议题是, 使用先前的研究信息作为指定理论协方差的依据是否是合适的。诚然, 既往研究中确实存有使用相似主题的研究结果作为统计检验力分析过程中设定参数依止的先例, 但有研究者指出, 这种指定方式可能错误地在统计检验力分析过程中混入了抽样误差而降低了统计检验力的可靠性, 并进一步提出了纠正该误差的方案(Liu & Wang, 2019)。对该问题的深入讨论已超出了本文的范畴, 有兴趣的读者可以进一步阅读Liu和Wang (2019)的研究。

5.3 非中心χ2分布近似带来的误差

Satorra-Saris法与MacCallum法这两种分析方法从本质上来说都是利用非中心χ2分布作为当H成立时样本似然比统计量T分布的近似。Steiger等人(1985)指出, 这种近似当且仅当样本满足似然函数关于分布的基本假设、样本量不太小、拟合函数值不是太大的情况下成立。诚然, Satorra等人(1991)的研究进一步指出, 当样本服从正态分布且理论模型与实际数据的偏离程度不是十分严重时, 即使对小样本而言, 这种利用非中心χ2分布进行近似的精度也是基本令人满意的。但对于分布假设不满足时这种近似的精度是否仍令人满意, 目前仍缺乏相关研究的分析。这意味着研究者在对结构方程模型的统计检验力进行分析时, 应当充分了解样本分布情况与所选结构方程模型参数估计方法之间的适配性, 在进行统计检验力分析和实际进行数据处理时使用同样的估计方法, 在样本分布偏离正态分布的情况下, 也可以考虑换用适用范围更广的Monte Carlo法进行统计检验力分析。目前主流软件提供的参数估计方法中, 极大似然法(maximum likelihood, ML)和广义最小二乘法(generalized least squares, GLS)要求数据为正态分布, 加权最小二乘法(weighted least squares, WLS)、非加权最小二乘法(unweighted least squares, ULS)和对角线加权最小二乘法(diagonally weighted least squares, DWLS)对数据分布要求不高, 但ULS属于尺度依赖方法(scale-dependent method), 使用时最好保证各个变量的测量单位统一, 而WLS和DWLS通常则需要1000以上的样本量(吴明隆, 2010)。

此外, Satorra-Saris法在使用非中心χ2分布对样本似然比统计量T的分布进行近似时, 同时使用模型拟合“真实总体”得到的统计量作为对非中心参数的估计。这意味着使用Satorra-Saris法分析模型参数检验的统计检验力时, 检验方法本身也会对结果产生影响。本文4.2部分模型参数检验的先验检验力分析中, Monte Carlo法与Satorra-Saris法对同一检验的分析得出了差异较大的结果就是这个原因。在该例中, 在设定α = 0.05,= 401的情况下, 使用Wald检验、LM检验和似然比检验得到的统计量对非中心参数进行估计时得到的非中心参数分别为13.399, 22.658和23.265, 对应的统计检验力分别为0.955, 0.997和0.998。使用Monte Carlo法对三种方法进行统计检验力分析, 得到的结果则分别为0.996, 0.998和0.998。这提示研究者在使用Satorra-Saris法分析Wald检验的统计检验力时, 可能会由于低估统计检验力而高估所需要的样本数量。

5.4 Monte Carlo法的精度与计算效率

诚然Monte Carlo法由于可以广泛适用于各类检验场景, 且在模拟次数足够多的情况下得出的统计检验力的估计值依概率收敛于其理论真值, 使得该方法广泛受到研究者的青睐。但Monte Carlo法同样面临着结果不稳定以及计算效率低下的情形。与其他两种方法不同, Monte Carlo法得到的计算结果并不是一个确定值, 而是一个随机变量, 该随机变量的期望值等于统计检验力的真实值, 这就导致了对同一个假定样本量进行多次统计检验力分析时可能会得出不同的结果。这意味着研究者在使用Monte Carlo法进行统计检验力分析时求得的样本量理应为一约数而非确切值。换言之, Monte Carlo法无法像Satorra-Saris法或MacCallum法那样给出“理论上达到目标统计检验力所需的最小样本量”。这也同时意味着通过缩短采样间距的方式对基于Monte Carlo法的统计检验力分析的精度的提升是有限的。

此外, Monte Carlo法的计算效率一直以来也是比较困扰研究者的一个问题。与Satorra-Saris法和MacCallum法误差不同, Monte Carlo法的误差来源主要是模拟样本带来的偶然误差。根据De Moivre-Laplace中心极限定理, 随着重复次数的提升, Monte Carlo法所得到的统计检验力估计值的标准差会降低, 但其降低速率与重复次数之间并非线性关系, 而是二次关系。换言之, 若研究者希望将Monte Carlo法得到的估计值的精度提高一个数量级(相当于让估计值的标准差降低为原来的0.1倍), 则需要将扩大为原来的100倍。这大大降低了Monte Carlo法的计算效率。并且, Monte Carlo法本身计算起来就比较耗时, 在CPU主频为2.50 GHz的笔记本电脑上运行本文中关于中介模型统计检验力分析的R程序, 当设定重复次数= 1000, 样本量= 401时, 使用Monte Carlo法分析Wald检验统计检验力所需的时间大致为60 s (单线程); 若将检验方法更换为LM检验或似然比检验, 执行同样的分析所需时间则上升到约900 s (单线程); 若对非参数Bootstrap检验的统计检验力进行分析, 即使采用并行计算技术将任务分配到多线程计算机的不同线程上处理, 所需时间通常也会超过一个小时。此时若反复设定样本量甚至参数进行多轮分析从时间上来说是不经济的。诚然有学者指出此时可以换用参数Bootstrap法(或与之等价的MC法)简化计算过程, 节省计算时间(Schoemann et al., 2017), 但这种更换也将在一定程度上造成统计检验力估计时的误差。

5.5 不同拟合指数的选择对MacCallum法的影响

本文主要介绍了用MacCallum法对RMSEA相关的零假设进行统计检验力分析的理论与实践。事实上, MacCallum法可以用于多种拟合指数的情形。MacCallum和Hong (1997)将该方法进一步扩展到了针对GFI和AGFI相关零假设的情形。Kim (2005)则提出了当零假设是关于RMSEA、CFI、MFI和GFI这四种参数其一时估算样本量的简便公式。值得注意的是, 上述参数间的换算关系还会受到模型本身的影响。因此, 目前学界主流建议的拟合指数界值在不同的模型中并不等价, 这就导致了针对同一个计划模型, 采用不同拟合指数进行先验检验力分析时, 可能得出不同的结果。例如, 根据温忠麟等人(2004)的建议, 评估模型拟合时, MFI的建议界值为0.85, RMSEA的建议界值为0.08。此时, 对于不同自由度的模型而言, 依据这两个指标的建议界值计算出的计划样本量也有所不同。以计划显著性水平为0.05, 统计检验力为0.95的情况为例, 当模型自由度为10时, 根据MFI和RMSEA计算出的计划样本分别有77人和383人; 当模型自由度为50时, 根据MFI和RMSEA计算出的计划样本分别有134人和136人; 而当模型自由度为100时, 根据MFI和RMSEA计算出的计划样本则分别有176人和90人。因此, 本文建议研究者在使用MacCallum法进行先验检验力分析时, 使用多种拟合指数构建假设进行检验, 并在所有计划样本量中选取最大值。至于拟合指数的具体选择, 可以参考温忠麟等人(2004)的研究。

5.6 评价模型拟合时的统计检验力分析与等效性检验

如前所述, 既往研究中对传统χ2检验的一个批评就是该检验将想要验证的假设作为零假设, 在结果报告中又缺乏对其Ⅱ类错误发生概率的分析, 使其无法真正起到验证模型的作用(王阳等, 2020)。而等效性检验实质上就是通过构建一个“可接受的差异”标准的方式重写零假设, 从而将想要验证的假设重新放回了备择假设的位置, 在一定程度上, 也可以将等效性检验视作一种“颠倒了H与H的传统χ2检验”。根据MacCallum等人(1996)的研究, 可以推知, 对H0a:F≤k, 且真实参数为F=k的情形, 存在一种与之“对偶”的情形: H0b:F≥k, 且此时的真实参数为F=k, 这两种情形下Ⅰ类错误概率和Ⅱ类错误概率互相为对方的Ⅱ类错误概率与Ⅰ类错误概率。这意味着, 对传统χ2检验而言, 在进行先验检验力分析时, 若研究者参考等效性检验中的H设定F的真值(即F的真值不小于ε0), 并设定显著性水平为α, 统计检验力为1−β计算出计划样本量。那么同样可以保证在控制显著性水平为β的水平下, 对实际拟合良好的模型(即F= 0), 采用零假设为H:F≥ ε0的等效性检验进行检验时, 正确拒绝零假设的概率为1−α。因此, 本文建议研究者在对评估模型拟合相关的假设检验进行统计检验力分析时, 设定不小于0.95的统计检验力。这样可以保障在模型拟合较差的情况下, 研究者错误地认为模型拟合良好的可能性不高于0.05。

6 总结

本文主要介绍了结构方程模型假设检验统计检验力分析的三种代表方法: Satorra-Saris法、MacCallum法和Monte Carlo法, 这些方法各有自己的适用情形。相比于目前已被广大研究者所熟知的平均数差异检验的统计检验力分析, 结构方程模型的统计检验力分析对研究者的统计水平有更高的要求, 并且检验过程较为复杂。综合考虑易掌握和易使用两方面的要求, 本文建议研究者在研究设计的过程中根据自己需要进行的检验类型选择恰当的统计检验力分析方式, 具体可以参考图2进行选择。

图2 结构方程模型统计检验力分析方法选择建议

注: 未标注理论协方差矩阵生成方法的表示研究者可以参照5.2部分的建议自行设定

致谢：感谢刘力沛博士对本文英文摘要的修改, 感谢崔虞馨、姜鹤、荣杨在本文修改、定稿过程中提供的诸多帮助, 感谢两位匿名审稿人对本文提供的宝贵意见。

方杰, 张敏强, 李晓鹏. (2011). 中介效应的三类区间估计方法.(5), 765−774.

屠金路, 金瑜, 王庭照. (2005). Bootstrap法在合成分数信度区间估计中的应用.(5), 1199−1200.

王阳, 温忠麟, 付媛姝. (2020). 等效性检验——结构方程模型评价和测量不变性分析的新视角.(11), 1961−1969.

文书锋, 汤冬玲, 俞国良. (2009). 情绪调节自我效能感的应用研究.(3), 666−668.

温忠麟, 侯杰泰, 马什赫伯特. (2004). 结构方程模型检验: 拟合指数与卡方准则.(2), 186−194.

温忠麟, 叶宝娟. (2014a). 有调节的中介模型检验方法:竞争还是替补?(5), 714−726.

温忠麟, 叶宝娟. (2014b). 中介效应分析: 方法和模型发展.(5), 731−745.

吴明隆. (2010).——(第2版). 重庆大学出版社.

吴艳, 温忠麟. (2011). 与零假设检验有关的统计分析流程.(1), 230−234.

叶宝娟, 温忠麟. (2012). 用Delta法估计多维测验合成信度的置信区间.(05), 1213−1217.

张涵, 康飞. (2016). 基于Bootstrap的多重中介效应分析方法.(5), 75−78.

张莉, 薛香娟, 赵景欣. (2019). 歧视知觉、抑郁和农村留守儿童的学业成绩: 纵向中介模型.(3), 584−590.

赵礼, 王晖. (2019). 统计检验力的分析流程与多层模型示例.(5), 276−283.

Chou, C.-P., & Bentler, P. M. (1990). Model modification in covariance structure modeling: A comparison among likelihood ratio, lagrange multiplier, and wald tests.(1), 115−136.

Cohen, J. (1988).(2nd ed.). Hillsdale, NJ: Erlbaum.

Efron, B. (1979). Bootstrap Methods: Another Look at the Jackknife.(1), 1−26.

Gonzalez, R., & Griffin, D. (2001). Testing parameters in structural equation modeling: Every "one" matters.(3), 258−269.

Hoenig, J. M., & Heisey, D. M. (2001). The abuse of power: The pervasive fallacy of power calculations for data analysis.(1), 19−24.

Hollerbach, P., Johansson, A., Ventus, D., Jern, P., Neumann, C. S., Westberg, L., ... Mokros, A. (2018). Main and interaction effects of childhood trauma and the MAOA uVNTRpolymorphism on psychopathy., 106−112.

Jak, S., Jorgensen, T. D., Verdam, M., Oort, F. J., & Elffers, L. (2021). Analytical power calculations for structural equation modeling: A tutorial and shiny app.(4), 1385−1406.

Kim, K. H. (2005). The relation among fit indexes, power, and sample size in structural equation modeling.(3), 368−390.

Kornadt, A. E., Siebert, J. S., & Wahl, H.-W. (2019). The interplay of personality and attitudes toward own aging across two decades of later life.(10), Article e0223622. https://doi.org/10.1371/journal.pone.0223622

Liu, X., & Wang, L. J. (2019). Sample size planning for detecting mediation effects: A power analysis procedure considering uncertainty in effect size estimates.(6), 822−839.

MacCallum, R. C., Browne, M. W., & Li, C. (2006). Testing differences between nested covariance structure models: Power analysis and null hypotheses.(1), 19−35.

MacCallum, R. C., Browne, M. W., & Sugawara, H. M. (1996). Power analysis and determination of sample size for covariance structure modeling.(2), 130−149.

MacCallum, R. C., & Hong, S. (1997). Power analysis in covariance structure modeling using GFI and AGFI.(2), 193−210.

MacKinnon, D. P., Lockwood, C. M., & Williams, J. (2004). Confidence limits for the indirect effect: Distribution of the product and resampling methods.(1), 99−128.

Marcoulides, K. M., & Yuan, K.-H. (2017). New ways to evaluate goodness of fit: A note on using equivalence testing to assess structural equation models.(1), 148−153.

Moshagen, M., Erdfelder, E. (2016). A new strategy for testing structural equation models.(1), 54−60.

Mullen, P. R., & Crowe, A. (2017). Self-stigma of mental illness and help seeking among school counselors.(4), 401−411.

Muthén, B. O. (2004).. CA: Muthén & Muthén.

Muthén, L. K., & Muthén, B. O. (2002). How to use a Monte Carlo study to decide on sample size and determine power.(4), 599−620.

Preacher, K. J., & Coffman, D. L. (2006).[Computer software]. Retrieved September 10, 2021, from http://quantpsy.org/ rmsea/rmsea.htm

Preacher, K. J., & Selig, J. P. (2012). Advantages of Monte Carlo confidence intervals for indirect effects.(2), 77−98.

Rosseel, Y. (2021).. Retrieved September 10, 2021, from https://lavaan.ugent.be/tutorial/tutorial.pdf

Satorra, A. (1989). Alternative test criteria in covariance structure analysis: A unified approach.(1), 131−151.

Satorra, A., & Saris, W. E. (1985). Power of the likelihood ratio test in covariance structure analysis.(1), 83−90.

Satorra, A., Saris, W. E., & Pijper, W. M. (1991). A comparison of several approximations to the power function of the likelihood ratio test in covariance structure analysis.(2), 173−185.

Schoemann, A. M., Boulton, A. J., & Short, S. D. (2017). Determining power and sample size for simple and complex mediation models.(4), 379−386.

Steiger, J., Shapiro, A., & Browne, M. (1985). On the multivariate asymptotic distribution of sequential chi-square statistics.(3), 253−263.

Venables, W. (1975). Calculation of confidence intervals for noncentrality parameters.(3), 406−412.

Wang, Y. A., & Rhemtulla, M. (2021). Power analysis for parameter estimation in structural equation modeling: A discussion and tutorial.(1), 1−17.

Yuan, K.-H., & Chan, W. (2016). Measurement invariance via multigroup SEM: Issues and solutions with chi-square- difference tests.(3), 405−426.

Yuan, K.-H., Chan, W., Marcoulides, G. A., & Bentler, P. M. (2016). Assessing structural equation models by equivalencetesting with adjusted fit indexes.(3), 319−330.

Zhai, H.-K., Li, Q., Hu, Y.-X., Cui, Y.-X., Wei, X.-W., & Zhou, X. (2021). Emotional creativity improves posttraumatic growth and mental health during the COVID-19 pandemic., Article 600798.https://doi.org/ 10.3389/fpsyg.2021.600798

Zhang, X. J., & Savalei, V. (2016). Bootstrapping confidence intervals for fit indexes in structural equation modeling.(3), 392−408.

Zhang, X., & Zaman, B. U. (2020). Adoption mechanism of telemedicine in underdeveloped country.(2), 1088−1103.

Zhang, Z. Y. (2014). Monte Carlo based statistical power analysis for mediation models: Methods and software.(4), 1184−1198.

Zhang, Z. Y., & Wang, L. J. (2020).[Computer software]. Retrieved December 11, 2021, from https://CRAN. R-project.org/package=bmem

Power analysis in structural equation modeling: Principles and methods

ZHAI Hongkun, LI Qiang, WEI Xiaowei

(Department of Social Psychology, Nankai University, Tianjin 300350, China)

Structural equation modeling (SEM) is an important statistical tool in psychology, management, and sociology. However, the lack of analyses and reports of statistical power in many studies using SEM has reduced the probative power of the study results. There are three main types of statistical power analysis methods for SEM: the Satorra-Saris, MacCallum, and Monte Carlo methods. The Satorra-Saris method applies to cases where the alternative model is clear, analysis object is simple, and the statistic to be examined is based on the χ2distribution. The MacCallum method is applicable to the case of χ2-based overall model fit tests with unknown alternative models. Further, the Monte Carlo method applies to cases where the analysis object is complex, or the test is performed using simulation or resampling methods. In practice, researchers should clarify the purposes and methods of the test as well as the availability of alternative models as a priority. The research method can then be determined on the basis of the above information.

structural equation model, statistical power, fitting test, test of model parameters

B841

2021-10-09

*国家社会科学基金项目(19ASH012)资助。

魏晓薇, E-mail: mcqueen91@163.com