基于AHP-RMM的既有建筑结构安全风险评估研究
2022-09-07王健李红民张家瑞闫凯丁蕾
王健 李红民 张家瑞 闫凯 丁蕾
(1.山东建筑大学信息与电气工程学院,山东 济南 250101;2.山东建筑大学土木工程学院,山东 济南 250101;3.山东省智能建筑技术重点实验室,山东 济南 250101)
0 引言
随着既有建筑使用年限的增加,其安全问题成为社会关注的焦点。建筑结构一旦出现安全问题,不仅会威胁人民的生命安全,而且会造成恶劣的社会影响。因此,对既有建筑结构进行安全风险评估对于防范和化解重大建筑事故风险具有重要意义。
影响建筑结构在役状态的因素较多,如温度、风力等外部环境因素,因此,结构安全风险评估难度较大。高辉等[1]将模糊层次分析法应用于混凝土工程质量风险分析与评价,得出与实际相符的工程质量风险评价结果;喻岩[2]、黄慎江等[3]运用传统9标度法确定评价指标权重,采用模糊层次分析法分别对钢结构工业建筑和工业厂房进行了可靠性分析;陈为公等[4]通过建立考虑脆弱性的装配式建筑安全评价体系,引入有序加权平均算子,通过模糊综合评价对青岛市三个装配式项目进行实证分析,提出了与实际安全水平相符的评估结果;江杰等[5]采用区间层次分析法和熵权法相结合的模糊评价方式,对南宁市5层砖混结构住宅楼进行了安全评估;徐泽水[6]通过模拟评估,指出10/10~18/2标度最适宜用于精确权值计算,且评价结果较为合理;骆正清等[7]对层次分析法中的常用标度进行对比分析,得出的结论仅适用于理论证明或经验总结,对于特定工程的实际应用有待进一步研究。通过分析相关研究文献可知,工程结构风险贯穿于工程建设的全生命周期[8-10]。目前,虽然针对建筑施工风险评估的研究成果较多,但缺乏针对既有建筑整体结构安全风险评估的研究。
鉴于此,本文采用AHP-RMM的综合评价方法,通过确定既有建筑结构风险源,利用AHP建立风险评估模型,并结合风险矩阵法建立各指标隶属度函数,根据综合评估结果确定风险等级和应对策略,以期为既有建筑结构安全风险评估提供参考。
1 建立既有建筑安全风险评估指标模型
建筑结构往往具有体量庞大、结构复杂等特点,从系统工程的角度可以视为复杂系统。以层次分析法为基础,在参考《建筑结构可靠性设计统一标准》(GB 50068—2018)、《民用建筑可靠性鉴定标准》(GB 50292—2015)[11-12]的基础上建立评估指标模型[3]。该评估模型由承重结构、地基基础、结构及支撑部分和维护结构所构成的项目层及承载能力、构造连接、裂缝、变形等指标层构成,如图1所示。

图1 既有建筑结构安全风险评估模型
2 既有建筑结构安全风险综合评估
2.1 确定评判因素集
既有建筑结构安全风险影响因素众多,对其进行安全风险评估首先应建立合理的体系框架。若评判因素集中指标过多,易削弱主要指标的贡献作用;若因素集中指标过少,则不能完全考虑建筑结构整体的安全水平。因此,确定评判因素集如下:首层为目标层,即整体建筑结构由综合评判得出的在役安全风险水平。第二层是项目层,目标层的综合评估结果由项目层中4个评判指标确定,项目层的评估结果由指标层确定。第三层是指标层,由4个评判指标下对应的具体指标组成,例如,承重结构项目X1可分为承载能力、构造连接、裂缝、变形4个评估指标,表示为X1=(X11,X12,X13,X14)。
2.2 确定评价集
工程实践表明,《民用建筑可靠性鉴定标准》(GB 50292—2015)和《危险房屋鉴定标准》(JGJ 125—2016)采用的分级原则能够有效判断既有建筑安全水平。参照上述规范标准,将既有建筑结构安全风险水平分为4个等级,表示为U={U1,U2,U3,U4}, 分别代表低风险、一般风险、较大风险和重大危险[13]。评估结果及处理措施见表1。

表1 评估结果及处理措施
2.3 单个项目模糊评判矩阵确定
第i个指标的隶属度cij(j=1,2,3,4)由隶属度函数计算得出。记Ci=(ci1,ci2,ci3,ci4)为单因素评估集,表示该指标下第i个指标评估结果。综合该指标下所有指标评估因素集,构成单层次模糊评判矩阵。以承重结构X1为例,模糊评判矩阵可表示为
(1)
式中,X1中的元素X1i隶属于Uj等级的程度为cij(0≤cij≤1)。同理,可得到其他指标的模糊评判矩阵。
2.4 评判权重确定
标度的选取是层次分析法赋权的关键。为便于对比分析,本文采用三种常用标度方法构建判断矩阵,标度值说明见表2。其中,指数标度中的λ取值在[1.1, 1.5]时符合实际结果,得出的判断矩阵与实际结果相符合,故本文λ取值为1.2[14]。
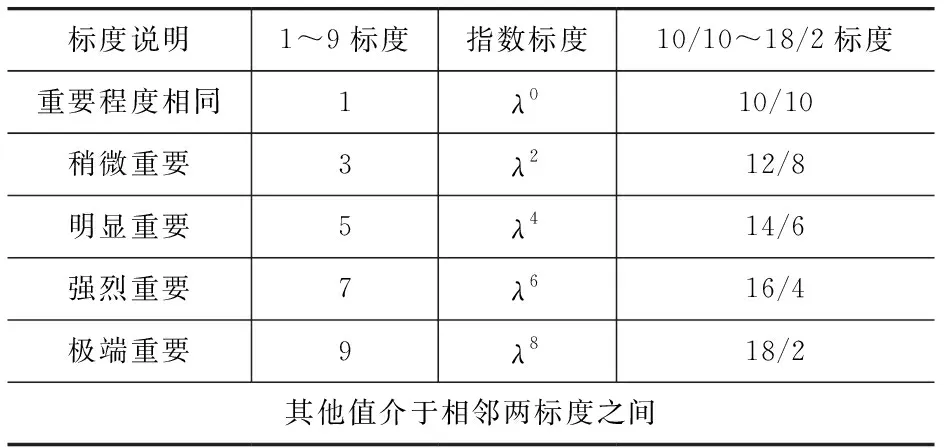
表2 标度值说明
根据比较判断矩阵计算最大特征值和所对应的特征向量,从而确定各指标评判权重。由最大特征值得到一致性指标CI,公式如下
(2)
基于比较判断矩阵的阶数n,由RI=

(3)
式中,若CR<0.1,则所构建的判断矩阵符合一致性要求;若CR≥0.1,则不符合一致性要求,需要调整比较矩阵。
2.5 选取模糊算子和计算评判指标
由于评估模型具有多指标、多因素的特点,考虑到承载能力等主导变量对评估结果具有重要影响,为使评估结果更符合实际运营情况,本文的模糊算子选择加权平均型算子M(+,·) 。评估结果B由模糊综合评判式(4)计算得到
B=ω×C=
(4)
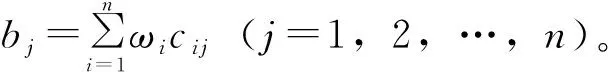
为避免实际评估中因局部构件损坏而出现风险等级隶属度不连续的问题,引入算数加权平均进行信息集成。本文以bj作为权重,对所有评价集元素Uj进行算数加权平均,得到建筑结构安全风险的最终评估结果。公式如下
(5)
式中,ai取值为[1, 4],分别对应评价集中各安全风险等级。
3 基于RMM的隶属度函数构建
建立既有建筑结构安全风险评估隶属度函数时,传统方法需要进行严格的计算分析与试验,同时,在很大程度上又依赖于已有的实际工程经验。鉴于此,本文引入风险矩阵分析法,综合考虑建筑结构安全风险发生的概率与致灾后果的严重性,将风险发生概率划分为5个等级,以估值1~5分别表示罕见、极少、偶尔、经常、频繁。风险发生概率P见表3。

表3 风险发生概率P
将风险致灾后果的严重性划分为5个等级,以估值1~5分别表示轻微、中等、严重、重大、灾难性,风险致灾后果C见表4[15]。由专家打分法确定各指标风险发生概率P和致灾后果C,将P与C的乘积作为风险值S。
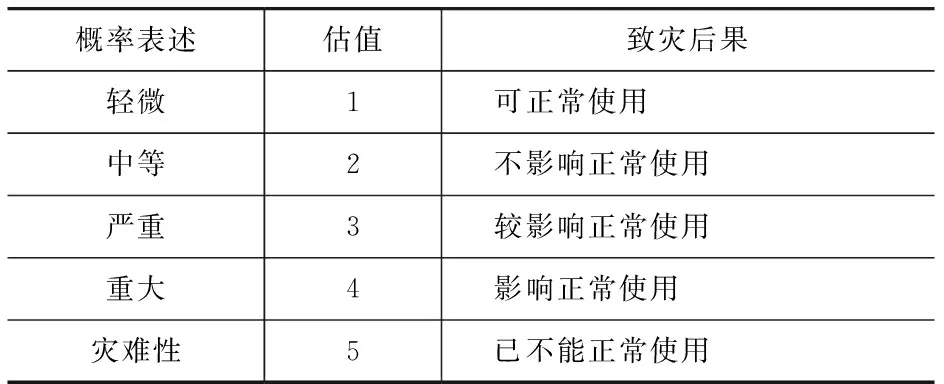
表4 风险致灾后果C
结合风险发生概率和风险致灾影响后果,建立风险评价矩阵,如图2所示。本文对建筑结构安全风险的评估是在正常条件下进行的,未将不可抗力(如自然灾害)考虑在内。

图2 风险评价矩阵
在参考既有建筑结构安全相关规范和标准的基础上,结合专家意见,确定风险边界值与既有建筑结构风险水平之间的对应关系,见表5。
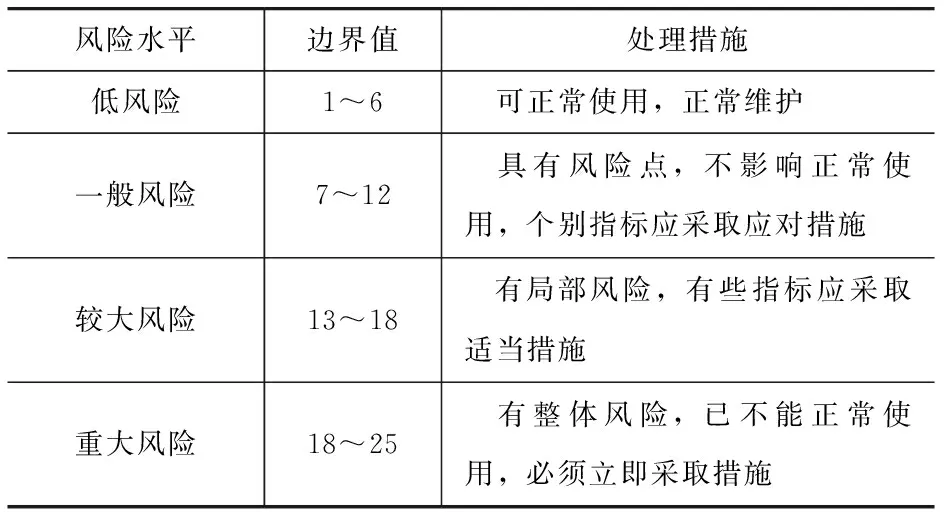
表5 风险水平与处理措施
考虑到半梯形和三角形组合分布能够细致处理边界值边缘信息,同时可以保存隶属度的边界信息,隶属度函数的建立采用半梯形和三角形组合而成的分布函数。定量隶属度函数见式(6)~式(9)。则风险值S对应评价集相应等级的隶属度函数为
(6)
(7)
(8)
(9)
4 实例分析
本文以某工业厂房建筑结构为评估对象,通过上述方法对其安全风险进行评估。各指标风险值见表6,风险值S由P与C的乘积计算得出。其中所用数据参考文献[3]。
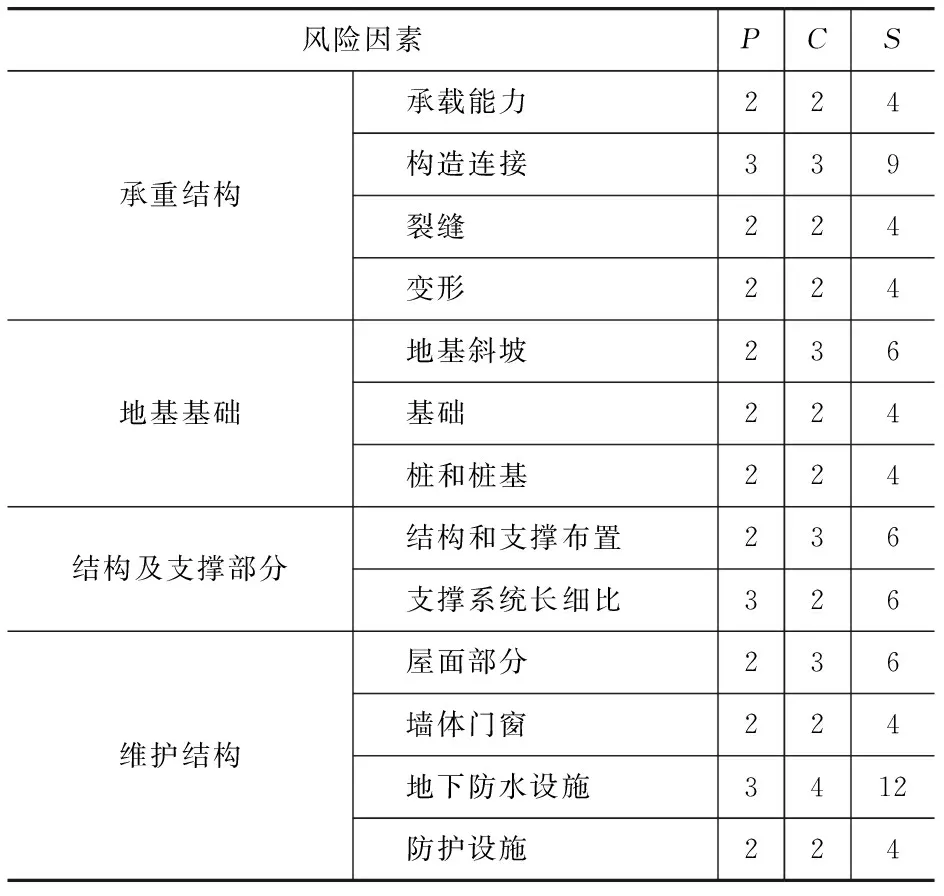
表6 各指标风险值
根据既有建筑结构安全风险评估方法,制定风险评估流程,如图3所示。具体计算步骤如下。
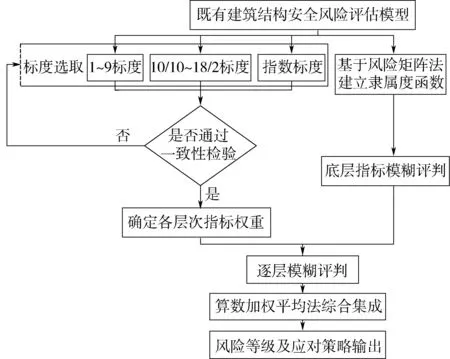
图3 既有建筑结构安全风险评估流程
4.1 建立评判矩阵并计算指标权重
根据评估模型中各指标间的相对重要程度,参照表2构造比较判断矩阵,由最大特征值和特征向量确定相应权重。建立指数标度下的比较判断矩阵,见表7。同理,建立其他两种标度评判矩阵。
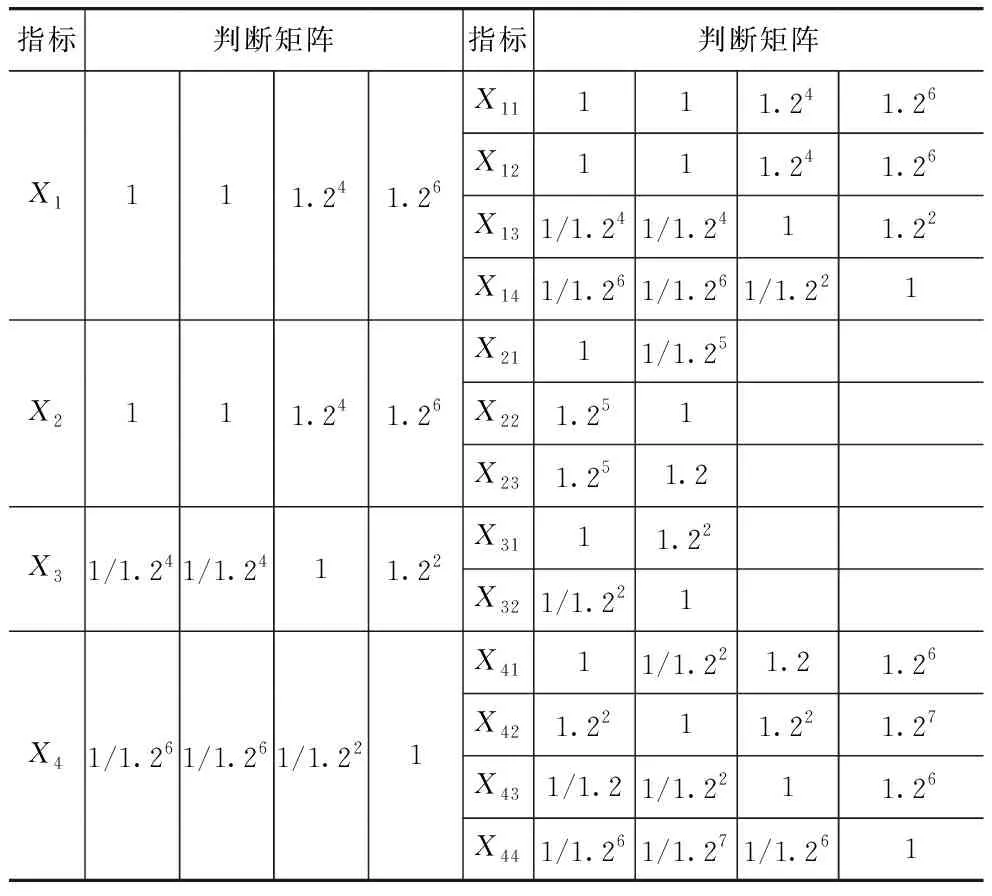
表7 基于指数标度的比较判断矩阵
为对比分析三种标度实际应用情况,计算三种不同标度下的权重值,见表8。
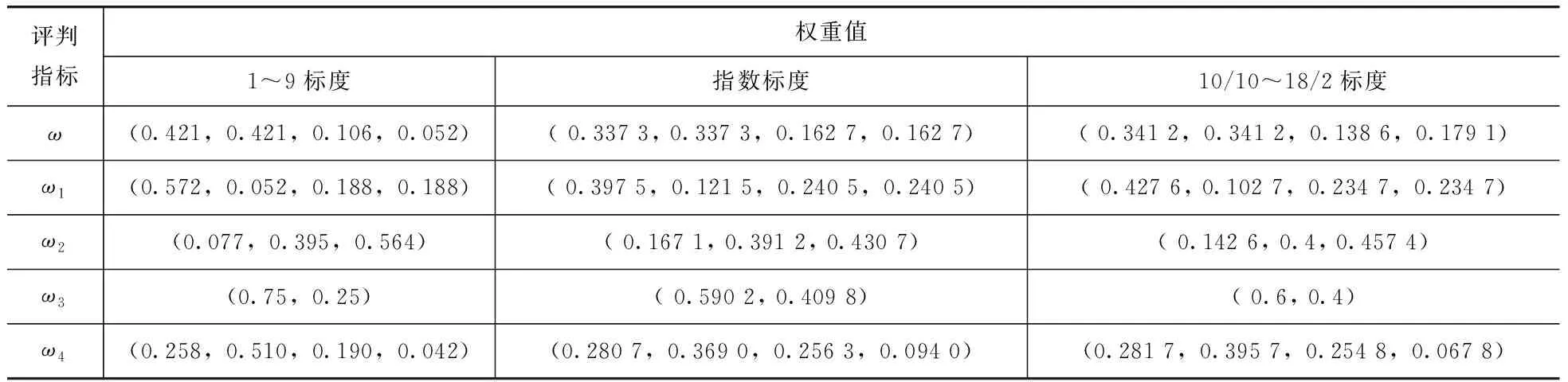
表8 三种权重值对比
4.2 计算评判矩阵
根据风险值S计算所有二级指标下各指标的隶属度,得到相应的评判矩阵,即
4.3 确定目标层评判结果
通过权重及单因素模糊评判矩阵逐层向上计算,求出既有建筑结构安全风险综合评判指标。三种标度下安全风险评估数值见表9。
4.4 结果分析
采用算数加权平均方式对评判矩阵B进行计算,得到评估结果U。以1~4分别表示低风险、一般风险、较大风险、严重风险4个等级。根据式(5)计算可知,U处于1~2,由此判断该工业厂房风险等级处于低风险和一般风险之间,即可常使用,但有安全风险点,个别指标应采取应对措施。实例分析结果表明:
(1)从三种不同标度的评判指标计算结果可见,指数标度在实际工程中的应用较1~9和10/10~18/2两种标度更符合实际。
(2)以评判矩阵B中元素bj为权重对评价集元素Uj进行算数加权平均后,三种标度均可得出U处于1~2的结果,由此可判断该工业厂房结构风险处于低风险和一般风险之间,即个别指标需要维护,结构整体较安全。
(3)在同样的工程实例下,文献[3]得出可靠度等级为二级的结论,与本文所述方法的研究结果大致相同,说明本文提出的既有建筑结构安全风险评估方法具有一定的可行性。
5 结语
本文将层次分析法和风险矩阵法相结合,在对比三种标度下评估结果准确性的基础上,通过模糊综合评价方法对既有建筑结构安全风险进行评估,并建立了既有建筑结构安全风险评估流程;通过引入算数加权平均法综合评估既有建筑结构安全风险后,在三种标度下均可得到相同评估结果;通过风险矩阵法建立隶属度函数,简化了常规隶属度函数构建方法,在既有建筑物安全风险综合评估中得到了符合实际的结果,可为既有建筑安全运维及风险管理提供参考。
