设有逆向可变车道交叉口信号配时模型研究
2022-09-07张赛赵欣酆磊陈曦
张 赛 赵 欣 酆 磊 陈 曦
(武汉理工大学交通与物流工程学院 武汉 430063)
0 引 言
随着城市机动车保有量的持续增长,城市道路面临的交通压力也日益增加,为了提高道路的通行效率,在部分交叉口设置可变车道来提高交叉口通行效率,但只考虑局部优化而忽略了全局,其配时及相序设置不尽合理,与设置可变车道的初衷背道而驰.
学者们针对可变车道或逆向可变车道(reverse variable lane, RVL)车道的相关理论进行了研究.奇兴族[1]基于交通波理论提出了RVL长度的确定方式.Lambert等[2]研究了可变车道的交通流特性,得出可变车道与一般道路的交通流特性具有相似性的结论.李灿等[3]通过对进口道交通流量、交通流向等因素进行分析对可变车道属性改变条件的阈值进行了研究.林浩等[4]对可变导向车道转向功能变换时刻及合理设置清空时间进行了研究.徐建闽等[5]提出了RVL及左转公交专用道设置方法. WONG[6]以交叉口通行能力最大化及周期最小化为目标,构建了二进制混合整数线形模型.孙锋等[7]以常规四路口设置RVL的交叉口为研究对象, 对其车道动态开关与信号配时方案的协同优化方法进行了研究,基于效率和安全为目标构建了RVL控制与信号参数的协同优化模型.任其亮等[8]建立了交叉口信号配时双目标优化模型,基于实验验证该模型能适用于低、中、高及不同左转比例的流量.
文中对设有RVL进口道的左转交通流分配出发,以交叉口平均延误及通行能力为优化因子与信号原始方案对比,研究能够使该类型交叉口整体最优的配时方案.
1 逆向可变车道设置原则
1.1 可变车道概念
将交叉口最内侧的一个车道或多个车道设置为可变车道,通过预信号控制,不同时间段内车道属性可作为出口道或进口道.
1.2 设置条件
参照商振华[9]提出的RVL设置条件,其可归纳为以下四点.
1) 交叉口必须为具有左转专用相位的平面交叉口.
2) 交叉口半径应满足相交道路的左转及右转.
3) 进口道道路资源紧张且左转交通流量大,交叉口饱和度需大于0.8.
4) 设置RVL的出口道,车道数量不少于三条.
2 逆向可变车道理论分析
2.1 冲突点分析
对于T形交叉口设置RVL,考虑其他进口道的右转都为渠化,则其的冲突车流仅为对向的直行车流(见图1a)),需在RVL开口处设置预信号,保证本相车流与对象车流的安全,合理的控制车辆的放行,见图1b).
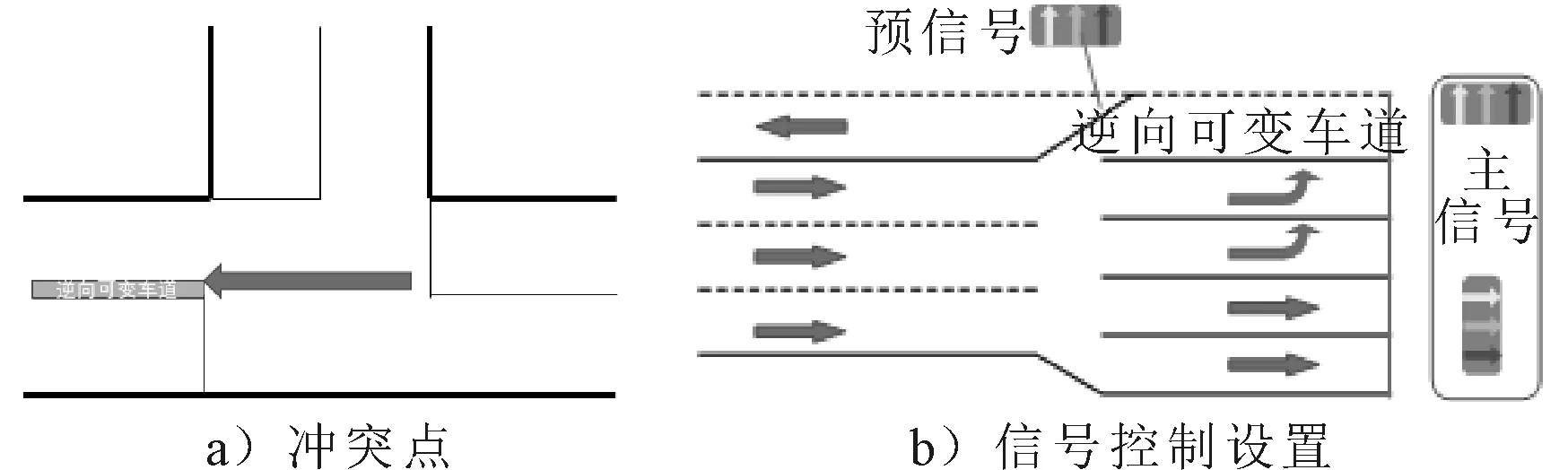
图1 RVL冲突点和信号控制设置
2.2 信号配时
文中所适用的相序方案方式有两种:对相放行,见图2a);按进口次序放行,见图2b).

图2 相序方案一和二
信号配时见图3.
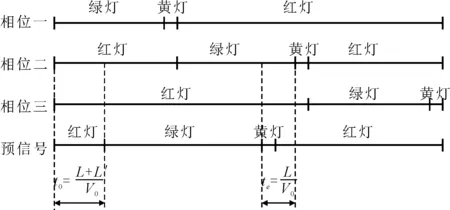
图3 信号配时示意图
2.3 逆向可变车道交通流分析
在一定时间段每个车道行驶的车流量为Qi,在交叉口拓宽段每个车道行驶的车流量为qi(见图4),RVL的车流量为qR,在不考虑渐变段有停滞车量的情况下,则有:
(1)

图4 流量分配
设有RVL方向进口道左转总交通量为QL,RVL的交通量为qR,常规左转车辆的分配比为m:n,则常规左转车辆的车流量分别为
预信号绿灯时间看做两个时间段,见图5,其中一个时间段为车辆进入RVL的时间,用Δt1表示,此时主信号未开始放行;另一时间段为放行时间,此时间段车辆可以进入交叉口放行,用Δt2表示,则RVL的长度需满足以下条件.
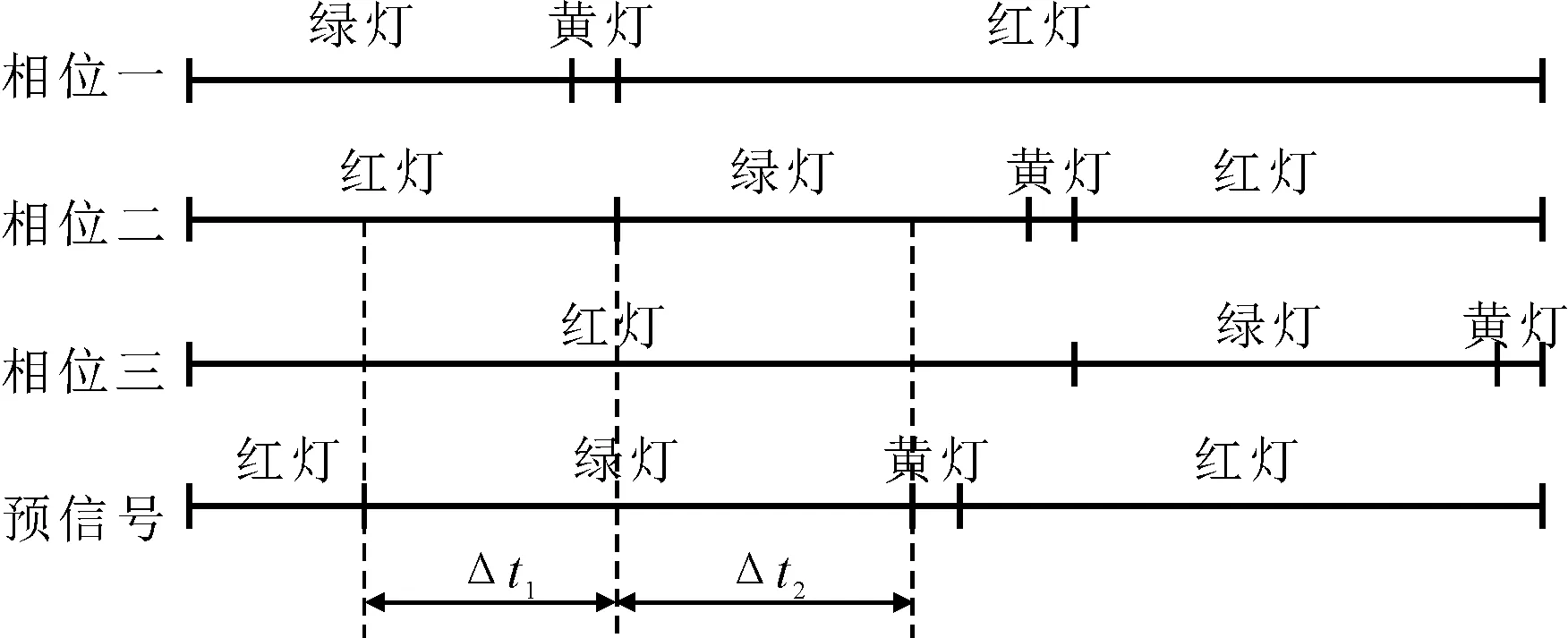
图5 RVL车辆通行时间段划分
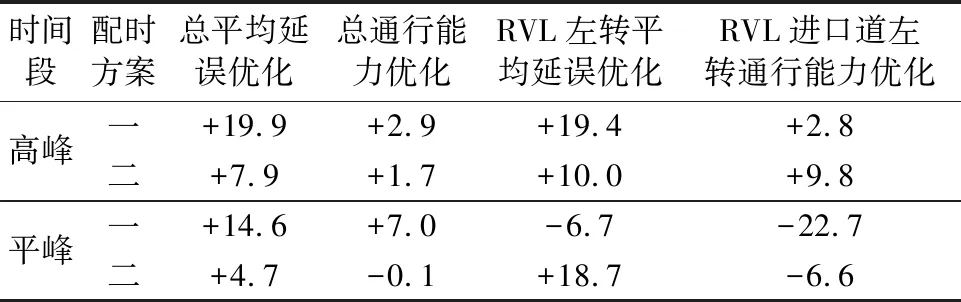
假设RVL的车辆到达分布服从泊松分布,其RVL的期望到达率为K,车辆的离开率为SR,即车道的饱和流率,通常情况下车辆的到达率小于车辆的离开率,即K g1=to+Δt1 (2) g2=te+Δt2 (3) (4) SR·(Δt2+te)≥K·(Δt1+Δt2) nl1+(n-1)ls≤LR≤LS 式中:n为RVL的容量,即Δt1时间最多能进入可变车道的车辆数;l1为车辆长度;ls为安全车间距;LR为RVL的长度;LS为距离上个交叉口距离.在Δt1时间内最多可达车辆为 (5) (6) 交通流量较低时,信号周期会短一些,为保证每个相位的车辆能在绿灯时间内安全通过,每个相位的绿灯时间不能低于15 s,交通量较大时,信号周期也会相应较长,考虑驾驶员的心理忍受程度,最大信号周期一般不超过200 s. (7) (8) (9) 式中:gmin为行人过街所需最短时间;LP为行人过街长度;vP为行人过街速度;I为绿灯间隔时间. 因此RVL的长度不同,其对应的左转车道的关键流量比也会不同. 交通控制的目的在于提高交叉口的通行效率,其通行效率主要体现在两个方面:交叉口的通行能力,因此通行能力应尽可能的大;驾驶员的驾驶体验,其由停车延误及停车次数来体现. Webster延误公式在低饱和状态比较适合,其默认车辆的延误累计是时间延续的,实际状态下的车辆到达及离开是离散状态,本研究针对饱和状态,因此车辆延误为 (10) (11) 式中:dij为第i相位第j车道的平均延误;qij为相应的关键流率;C为信号周期;λi为对应相位的绿信比;Li为对应相位的损失时间;A为黄灯时间;gei为对应相位有效绿灯时间,sij为相应的饱和流量;yij为qij与sij的比值. 此外RVL车辆到达车道开口处时会经历“匀速—减速—(怠速/停车)—加速—匀速”这一换道过程,其过程为 式中:v1为平均到达速度;ad为平均减速度;v0为平均怠速度;aa为通过可变车道时的平均加速度;v2为换道结束时的速度. 则其加、减速延误为 (12) 整个RVL的平均等待延误为 (13) 配时优化以交通延误越小,通行能力越大为目标函数,由于不存在使各个目标函数同时达到最优的解,所以只能将多目标问题转化为单目标问题,其目标函数为 (14) 式中:aims为目标优化值;d(ave)为优化后的平均延误;DN为原配时平均延误;CS为优化后的通行能力值;CN为原配时通行能力;α、β为相关系数. 采用饱和流率法计算交叉口通行能力: (15) 优化配时目的在于减少交叉口延误,提高交叉口通行能力,一般情况下交通量饱和度越大交通延误越大,所以交通延误与饱和度成正相关,随着交通量的提高,通行能力在目标函数中的占比应提高,在各路口饱和流率相同的情况下,周期越长通行能力越大,则其相关系数取值为 (16) (17) 式中:Y为各相位关键车道流率比之和.其约束条件为 (18) 交叉口目标优化函数涉及参数较多,且参数之间又牵涉不同的函数关系,可用于寻找数学模型中全局最优解问题,具有鲁棒性和并行性的特点,本文中RVL长度是模型关键,在长度确定后,设置相关的约束关系. 求解步骤如下. 步骤1初始化 设置最大进化代数,种群数,染色体个数,交叉概率,变异概率等相关参数.本文中编码对象为各相位的有效绿灯时间.因此染色体形式为[g1,g2,g3],其个数为三. 步骤2确定适应度函数 遗传算法在最优值探索过程中,一般无需其他外界信息,用于判断群体中个体的优劣程度指标.文中适应性函数为足够大的常数(F)减去aims: fitness=F-aims 步骤3选择 文中选择算子采用“轮盘赌选择法”,其方法为计算出每个个体的适应度函数,其被选择概率为 步骤4交叉运算分为两步:①将群体个体进行随机配对;②按照一定的交叉概率Pc使染色体对中对应染色体相互交叉,产生新的个体. 步骤5变异 变异运算,将个体染色体编码串中的某些基因组上的基因值以一定的概率Pm用该基因组的其他等位基因来替换,从而形成一个新的个体. 步骤6迭代终止 遗传运算的最大次数为N,当其迭代运算达到最大次数,则运算停止,或者染色体变化不大,群体趋于稳定时,迭代将终止.返回最优目标值. 选用武汉市中南路-武珞路交叉口,该路口中所有右转车道采用渠化设置,故不考虑右转车辆.基本交通量见表1,基础参数见表2.文中初始种群设置为50,遗传迭代次数为200次,交叉概率为Pc=0.8,变异概率为Pm=0.05. 表1 交叉口流量数据 表2 武珞路-中南路交叉口基本参数 寻优结果详见表3,表4为优化对比结果. 表3 寻优结果 表4 优化对比 单位:% 由表4可知: 1) 从交叉口整体角度出发,本文模型可在不同程度上对交叉口起到改善作用. 2) 采用本文模型寻优,在高峰时段优化更为显著,且全部为正优化. 3) 从交叉口整体角度出发,相序方案一的寻优结果较相序方案二而言,优化程度更好. 4) 平峰时段采用本文模型,会降低设有RVL进口道左转车道的通行能力. 1) RVL内的车辆到达分布服从泊松分布. 2) 选择RVL的车辆会经历一次主动变道,附带一次加减速延误. 3) 设有RVL的交叉口进口,常规左转车辆服从一定的比例. 以武汉市武珞路-中南路交叉口为例,对本文模型进行验证分析,基于交叉口整体优化的角度出发,本文模型在平高峰均能对交叉口起到改善作用,且在高峰时刻更为明显,采用方案一配时方案优化程度要比方案二更好,在平峰时间段设有RVL进口道左转车道的通行能力较原始方案降低,这也是本模型不足之处,只能保证全局最优而无法兼顾局部最优.3 目标求解
3.1 信号设置
3.2 延误计算
3.3 目标函数
3.4 基于遗传算法求解
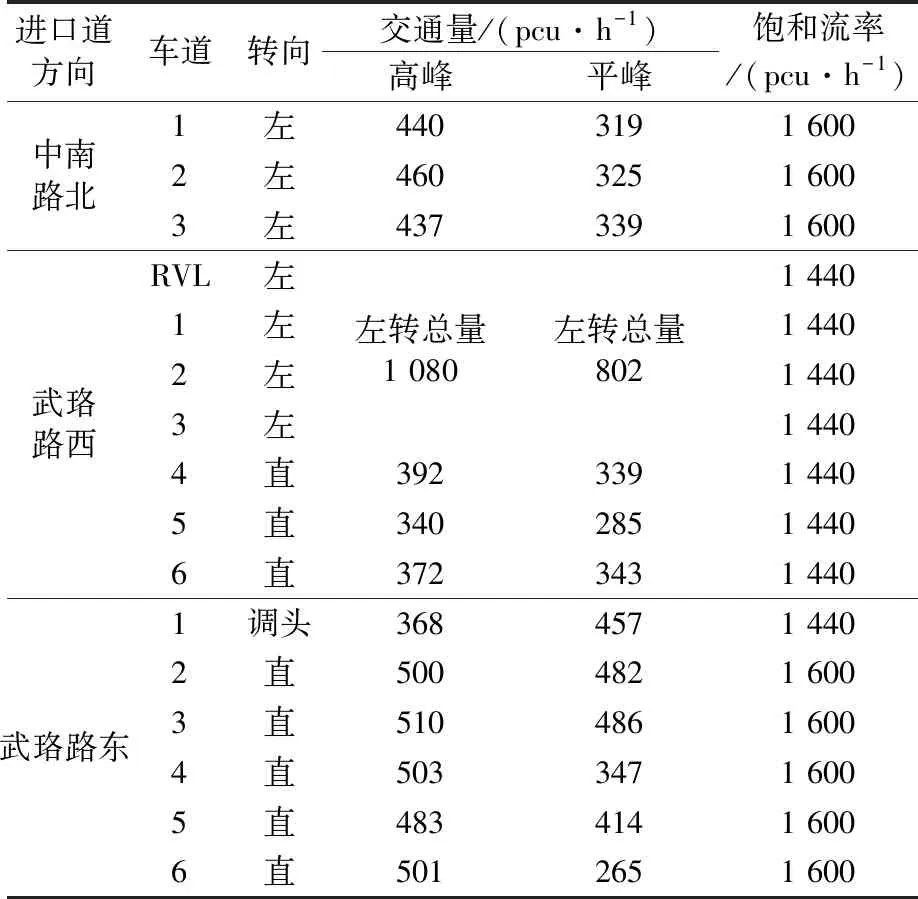
4 案例分析


5 结 论
