两类图运算的Zagreb 离心率指标

阿斯牙·米吉提

（喀什大学数学与统计学院，新疆 喀什 844000）

0 引言

设图G=(V,E)是一个简单连通的无向图,其中V(G)和E(G)分别表示图的顶点集和边集.对任意点u∈G，用degG(u)来表示点u的度数，且定义为从点u出发的边的总数目.设u0,u1,u2,…,uk∈V(G),e0,e1,e2,…,ek∈E(G)，其中ei是关联于结点ui-1和ui的边，则称u0e1u1e2u2e3…ekuk为连接u0到uk的路，路中边的数目称为路的长度.设任意两点u,v∈V(G),则u,v之间的距离定义为u,v之间最短路的长度，记为dG(u,v).而点u到v之间的最大距离称为点u的离心率，记为e(u)，即图G的离心率的总数ζ(G)定义为图G中所有顶点的离心率的总数，即ζ(G)=

图不变量是一个从图的集合到实数的函数.在化学图论中，图不变量通常被称为拓扑指标.在拓扑指标中，文献[1]中引入的Zagreb 指标是最著名的，其中Gutman 和Trinajstiċ研究了总π-电子能量对分子结构的依赖性，并在文献[2]中作了进一步研究.第一类Zagreb 指标和第二类Zagreb指标分别被定义为

这两个经典的拓扑指标反映了分子骨架的分支程[3].关于Zagreb 指标的各种结果见文献[4-9].与第一类和第二类Zagreb 指标类似,Vukičevic 和Hosseinazdeh[10]引入了Zagreb离心率指标，并定义

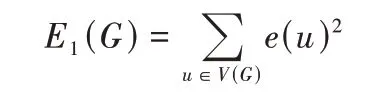
为图G的第一类Zagreb离心率指标，记为E1(G)；

定义

为图G的第二类Zagreb离心率指标，记为E2(G)；

定义

为图G的第三类Zagreb离心率指标，记为E3(G).

最近，又有一种新的图的点的离心率指标被引入，其中有拓扑离心连通指标、离心距离和n类离心Zagreb 指标等.进一步，有Xu[11]等人引入了衡量图的非自中心数，并定义

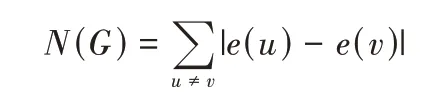
为图G的非自中心数，记为N(G).

关于这一指标仍有许多问题有待研究.在本文中,我们主要讨论通过图的复合运算与笛卡尔积运算得到的两类图的以上指标，并得到了这些图运算的第一、第二类、第三类Zagreb 离心率指标以及非自中心数(NSC 数)的精确表达式.

1 定义及引理

定义1.1设图G1和G2是任意两个无向的简单连通图,则G1和G2的笛卡尔积图为G=G1×G2,其中图G满足：V(G)=V(G1)×V(G2)；图G中的两个顶点(u1,v1)和(u2,v2)相邻当且仅当u1=u2,v1v2∈E(G2) 或者v1=v2,u1u2∈E(G1).

定义1.2设G1和G2是任意两个无向的简单连通图,则图G1和G2的复合图G=G1[G2]是顶点集为V(G1)×V(G2)、并具有不相交的顶点集V1和V2与边集E1和E2的图,且图中任意两个顶点(u1,v1)和(u2,v2)相邻当且仅当u1和u2相邻或者u1=u2,且v1和v2相邻.

引理1.1[12]设G和H是图,则有

（1）|V(G×H) |=|V(G)||V(H) |，|E(G×H) |=|E(G)||V(H) |+|V(G)||E(H) |；

（2）G×H是连通的当且仅当G与H都是连通的；

（3）如果(a,c)和(b,d)都是G×H的顶点,则有

引理1.2[13]若复合图G[?H]是连通当且仅当图G和H是连通的,则有

2 主要结果及证明

2.1 复合图的Zagreb 离心率指标及非自中心数

引理2.1设Pm和Pn分别为有m个顶点和有n个顶点的路,则对复合图Pm[Pn]，有

证明由离心率的定义可知又由引理1.2得

定理2.1设u=(ui,vj)为复合图Pm[Pn]中的一个顶点，e(u)为顶点u的离心率，则有

定理2.2设e=uv为复合图Pm[Pn]中一条边，e(u),e(v)分别为顶点u和v的离心率，则有

证明当m=2k+1时，即m为奇数时，

总之，无论m取偶数还是奇数，都有

定理2.3设e=uv为复合图Pm[Pn]中一条边,e(u),e(v)分别为顶点u和v的离心率,则有

证明当m=2k+1时，即m为奇数时,

定理2.4设e=uv为复合图Pm[Pn]中一条边,e(u),e(v)分别为顶点u和v的离心率,则有

总之，无论m取偶数还是奇数，都有

2.2 笛卡尔积图的Zagreb离心率指标及非自中心数

引理2.2设图G和H是简单图，则对于顶点(u,v)∈V(G×H),有

定理2.5设图G和H是简单图，则笛卡尔积图G×H的第一类Zagreb离心率指标为

定理2.6设图G和H是简单图，则笛卡尔积图G×H的第二类Zagreb离心率指标为

定理2.7设图G和H是简单图，则笛卡尔积图G×H的第三类Zagreb离心率指标为

定理2.8设图G和H是简单图，则笛卡尔积图G×H的非自中心数为

这里δ(G,H)是一个关于G和H的对称函数.