多目标粒子群算法在地铁速度曲线优化中的应用
2022-09-06黄江平钟晓静
黄江平,钟晓静
(华东交通大学电气与自动化工程学院,南昌 330013)
随着城轨列车运营里程的增加,城市轨道交通系统面临的压力也越来越大,要求最大程度地减少能源消耗,降低其运营成本和对环境影响[1]。截止2019年底,全国城市轨道交通运营里程从2064 km增长到6333.3 km。据统计,我国城市轨道交通每年用电量约15.26亿kW·h[2],同时,根据现有城市轨道交通能耗数据显示,列车牵引是列车耗能的主要因素,约为总能耗的50%[3]。因此,研究降低列车牵引能耗方法,对城市轨道交通建设具有重要的价值和意义。
HOWLETT等[4-5]用最大值原理证明了在直线道路上最佳驾驶策略是4种模式的组合,包括牵引、巡航、惰行和制动;MIYATAKE等[6]讨论了再生制动的列车节能策略,比较了梯度法、二次规划法的优劣。智能算法的迅速发展也为列车运行优化提供了更好的选择方案,段玉琼等[7]提出基于人工蜂群算法与操纵工况序列相结合的方法来优化计算,确定高速列车操纵工况关键转换点最优位置和速度。与此同时,李旭阳等[8]应用“四阶段”最优运行策略,以牵引能耗值和运行时间误差的权重作为目标函数,采用遗传算法进行优化;SHANG GUAN等[9]将时间和能耗作为2个优化目标,混合差分和模拟退火2种进化算法求解最优运行曲线。国内外学者虽然都对列车驾驶策略和运行曲线优化进行了深入研究,但在其选择上还有一些不足。比如,驾驶策略通常采用长时间巡航运行,以至在复杂路况下为保持匀速,列车需在“牵引-制动”下反复切换,导致能耗过大;而常规处理多目标问题的算法,通常是对多个目标进行加权求和,将其转换为单目标问题进行处理,这可能导致最终结果波动较大;同时,为便于分析计算往往采用单质点模型,不符合实际线路阻力变化情况。
综上所述,针对单质点和多质点建模的区别,同时考虑惰行工况对列车牵引能耗的影响,设置不同的控制策略加以比较,以列车运行时间和能耗作为优化目标,采用基于自适应网格的多目标粒子群算法,并对惯性权重采用线性微分递减法处理,获得Pareto[10]最优解集后,再结合模糊隶属度函数筛选最优方案,并与常规粒子群算法进行对比。最后,采用北京某地铁线路数据对算法进行验证。
1 列车模型构建
1.1 模型分析
为简化分析,通常将列车看成有质量无长度的单质点[11],而单质点模型在经过变坡点或变曲率点时列车所受附加阻力会发生突变,这与实际的附加阻力变化情况不符。因此,在单质点模型基础上进行改进,将列车视为多个质点构成的质点链,将每节车厢视为一个质点,同时每节车厢之间为刚性连接[12],每节车厢的运行状态与整个列车的运行状态相同。
由于多质点模型未忽略列车长度,故在实际线路中列车阻力变化情况与单质点模型不同。列车所受附加阻力中,隧道附加阻力只与隧道长度有关,模型影响不大,因此,主要分析不同模型下坡道及曲线附加阻力的变化情况。图1分别给出列车在不同模型下附加阻力的变化,仿真时以列车前端作为参照点。

图1 附加阻力变化
通过仿真结果可知,列车在经过变坡点及变曲率点的过程,坡道和曲线附加阻力是一个逐渐变化的过程,与单质点模型的突变相比多质点模型更贴合实际,减少误差。
1.2 列车运动方程
对列车的运动进行受力分析,通过牛顿第二定律推导,得出列车运动方程。

(1)

(2)
W(v)=(w1+w2+w3+w0)×G×M/1 000
(3)
w0=a+bv+cv2
(4)
式中,x为列车的位置;F牵为牵引力;B0为制动力;W(v)为列车运行阻力,w0为单位基本阻力,其中,a、b和c是与列车外观和机械结构相关的常数,w1为单位坡道附加阻力,w2为单位曲线附加阻力,w3为单位隧道附加阻力;ηq为牵引力使用系数;ηz为制动力使用系数;M为列车质量;γ为回转质量系数;G为重力加速度,通常取9.8 m/s2。
2 优化模型构建
列车优化问题是研究列车在运行过程中满足运行位移、限制速度、工况转换等约束条件下,搜寻最佳工况切换点。通过优化算法对建立的优化模型进行处理,获得最优的速度-距离曲线。
2.1 目标方程
列车运行状态通常有4种:牵引,巡航,惰行,制动。在此基础上对牵引总能耗E和运行时间T两个优化目标建立关系式。

(5)

(6)
式中,s为两站间的区间长度;x为列车运行时的位置;δ为再生制动反馈能量的效率。
2.2 评价指标
在保证列车准时性的同时,力求降低列车运行过程牵引能耗,将fE和fT作为评价指标。
fE=E
(7)
fT=T
(8)
式中,E为列车在整个区间的牵引能耗;T为列车实际运行时间。
2.3 目标及约束条件
根据上述目标方程和评价指标公式,建立多目标优化数学模型如下。
目标函数
F=min(fE,fT)
(9)
约束条件
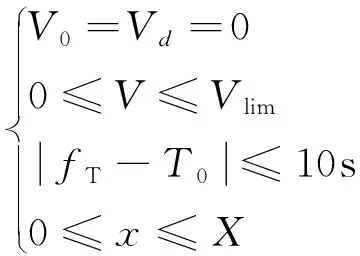
(10)
式中,V0和Vd分别为列车起始速度及终止速度;Vlim为区间线路的限制速度;X为列车最终运行位移,x为线路实际长度;T0为列车计划运行时间。
2.4 驾驶策略选择
传统的ATO驾驶策略在牵引过程后,列车通常将进入巡航工况,而在复杂的短距离路段中,长时间保持匀速会使得列车在牵引和制动之间反复切换,损耗很大[13]。因此,用牵引和惰行工况来代替巡航工况可有效降低列车牵引能耗。如图2所示,将驾驶策略分为未加入惰行、加入一次惰行及加入多次惰行3种控制策略。
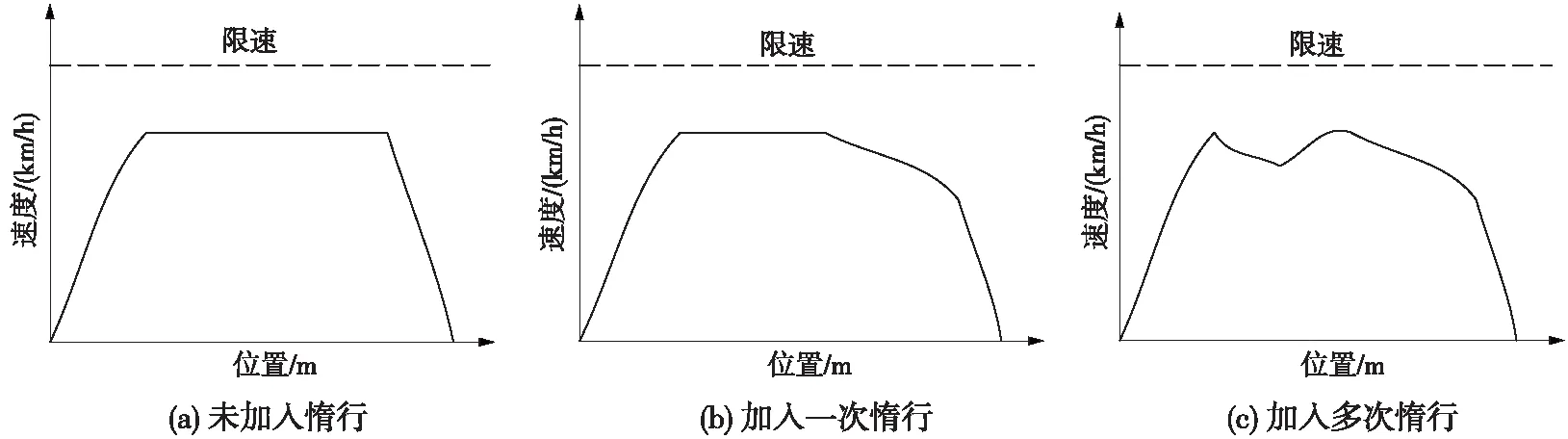
图2 列车控制策略
3 速度曲线优化算法
采用一种基于自适应网格的多目标粒子群算法(MOPSO based on adaptive grid algorithm,简称AGA-MOPSO)[14],将Pareto解集的概念引入到算法中,对每次迭代产生的Pareto最优粒子进行存档[15]。与将多目标加权求和转化为单目标的传统粒子群算法相比,该算法无论是在可行解的多样性及稳定性上,还是最后的优化效果上都更加出色。
3.1 基于自适应网格的MOPSO算法
算法求解的具体步骤如下。
(1)设置算法参数。种群数量M,外部存储数量N,加速度常量C1和C2,惯性权重Wmax,Wmin及粒子的维度(即工况转换点的个数)。
(2)初始化粒子种群,包括粒子群的位置pop[i](列车运行可能的工况转换点),速度V[i](工况转换点位置改变的量)。
(3)计算粒子目标函数值,确定粒子个体最优位置pbest[i]。构建自适应网格,通过Archive集中粒子的密度信息来选择出全局最优粒子gbest[i]。
(4)更新粒子群中粒子位置和速度公式。
V[i]=W×V[i]+rand( )×C1×(pbest[i]-
pop[i])+rand( )×C2×(gbest[i]-pop[i])
(11)
pop[i]=pop[i]+V[i]
(12)
式中,rand( )为范围[0,1]内的随机数。
(5)计算各个粒子的评价指标,利用支配关系更新个体最优粒子pbest[i]。
(6)对Archive集进行更新,同时对Archive集进行截断,保留N个最优解。
(7)判断是否满足设定的迭代次数,若否,则跳出程序,否则跳至第三步。若是,则结束迭代,输出Archive解集。
3.1.1 自适应网格的构建
把目标空间E-T(能耗-时间)以M×M的方式划分为M2个网格,每个网格的长宽计算如下
(13)

(14)
式中,M为Archive解集在当前迭代中解的个数;maxEt,minEt分别为迭代t次时Archive解集中列车运行能耗的最大和最小值;maxTt和minTt分别为迭代t次时列车运行时间的最大和最小值。
统计每个网格中粒子数量,将一个网格内解的个数作为粒子分布密度。图3给出了网格构建示意。
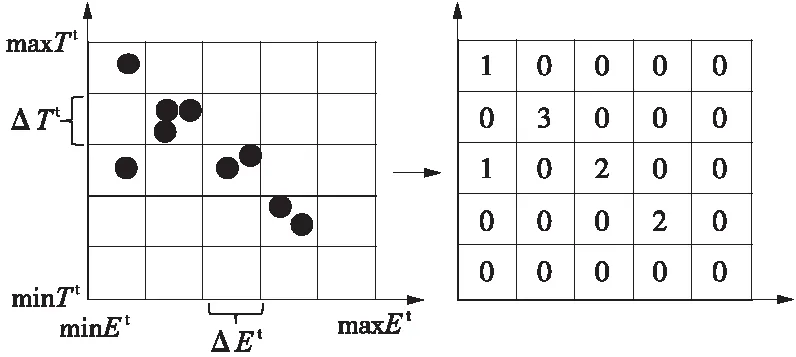
图3 自适应网格构建
3.1.2 Archive集的截断
为维持Archive集中解的数量,保证解分布的多样性及算法的全局搜索能力,要对外部存档进行删除。通过式(15)来计算粒子数量大于1的网格中要随机删除的粒子个数P。

(15)
式中,Int( )为取整函数;A为Archive集中的粒子数;N为要保留最优解的个数;Di为网格i的粒子个数。
3.2 惯性权重W
惯性权重W的变化对算法搜索能力有很大影响。与传统的线性递减法相比,采用线性微分递减法可以快速地收敛逼近于全局最优值,提高运算效率。W计算公式如下
(16)
式中,Wmax为惯性权重最大值;Wmin为惯性权重最小值;ta为总迭代次数;t为当前迭代次数。
3.3 Pareto解集中最优方案选择
采用模糊隶属度函数[16]对得到的Pareto解集中的每个解进行评价,以此来选出所有解中的最优方案。模糊隶属度函数如下
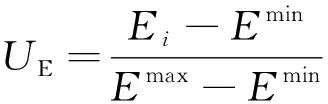
(17)
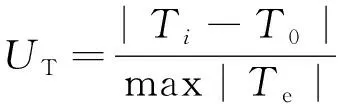
(18)
式中,UE,UT分别为能耗和准点误差的隶属度值;Emax和Emin分别为Pareto解集中能耗的最大、最小值;Ei为第i个解的能耗;T0为计划运行时间;Ti为第i个解的运行时间;Te为距离计划时间的误差。最优驾驶方案为UE与UT的和为最小值所对应的Pareto解。
4 仿真与分析
4.1 仿真参数设置
为验证算法的有效性,以北京地铁常用的B型列车为研究对象[17],选取北京某段地铁线路进行仿真研究。算法参数和线路基本参数分别如表1、表2所示,区间长2 810 m,最大坡度7‰,最大限速80 km/h,列车计划运行时间为190 s,列车实际运行时间为180~200 s,误差为±10 s。

表1 算法参数
4.2 两种算法分析对比
将传统PSO算法和AGA-MOPSO算法在相同驾驶策略下进行仿真实验。两种算法获得的解如图4所示。其中,PSO算法通过加权求和,将其转换为单目标优化问题,获得唯一最优解;而AGA-MOPSO引入Pareto解原理,获得一组由时间-能耗平衡的Pareto解集。

表2 线路参数
通过模糊隶属度函数对Pareto解集中的所有解进行评价,选出最优方案,如表3所示。与PSO相比,AGA-MOPSO获得的最优解在更加准时的同时可节能达7.4%。
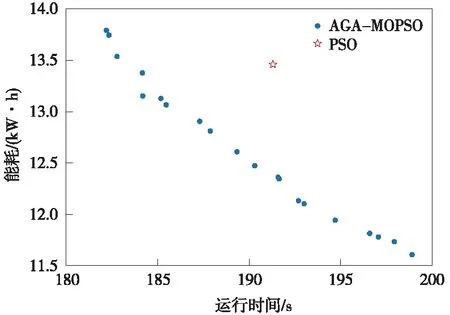
图4 两种算法的解

表3 最优方案对比
分别将两种算法独立运行20次,得到了每次优化获得的最优解的时间-能耗,如图5所示。
为比较两组数据的稳定程度,采用平均值、标准差及方差作为评价指标,分别对两种算法下的时间误差-能耗两个变量进行比较。
如表4所示,两种算法时间误差波动范围为2.12 s和2.76 s,相对于计划运行时间190 s来说影响不大,因此,时间误差波动可忽略,主要对能耗变量的波动进行描述。其中,PSO算法得到的能耗波动范围为2.02 kW·h,平均值为13.89 kW·h,方差为0.497;与之相比AGA-MOPSO算法的能耗波动范围更小为1.40 kW·h,平均能耗为12.48 kW·h,方差为0.137。因此,AGA-MOPSO算法获得的最终解波动范围更小,且更加稳定。

图5 算法稳定性比较

表4 两个变量评价指标描述统计
综上所述,对比两种算法,AGA-MOPSO算法优化得到最优解的效果比PSO算法更好,更加准时且能耗更小。同时,无论是解的多样性还是稳定性等方面都优于PSO算法。
4.3 不同控制策略对比
针对未加入惰行、加入一次惰行以及加入多次惰行3种不同控制策略,在利用AGA-MOPSO算法获得各自的Pareto解集后,采用上述模糊隶属度函数筛选出最优方案。表5为各种驾驶策略对应的最优驾驶方案。
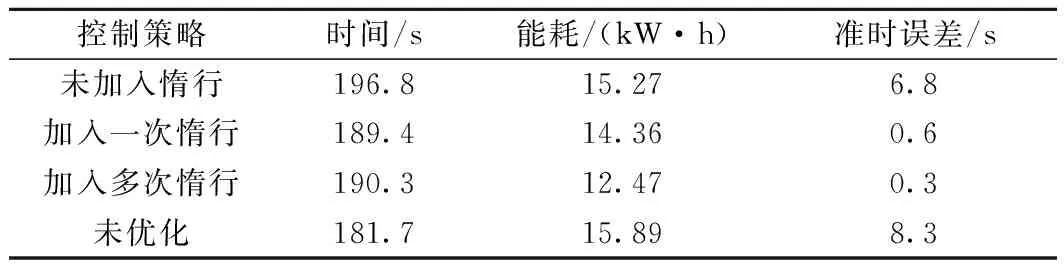
表5 不同控制策略下对应的最优方案
3种控制策略的最优方案所对应的速度-距离曲线如图6所示。
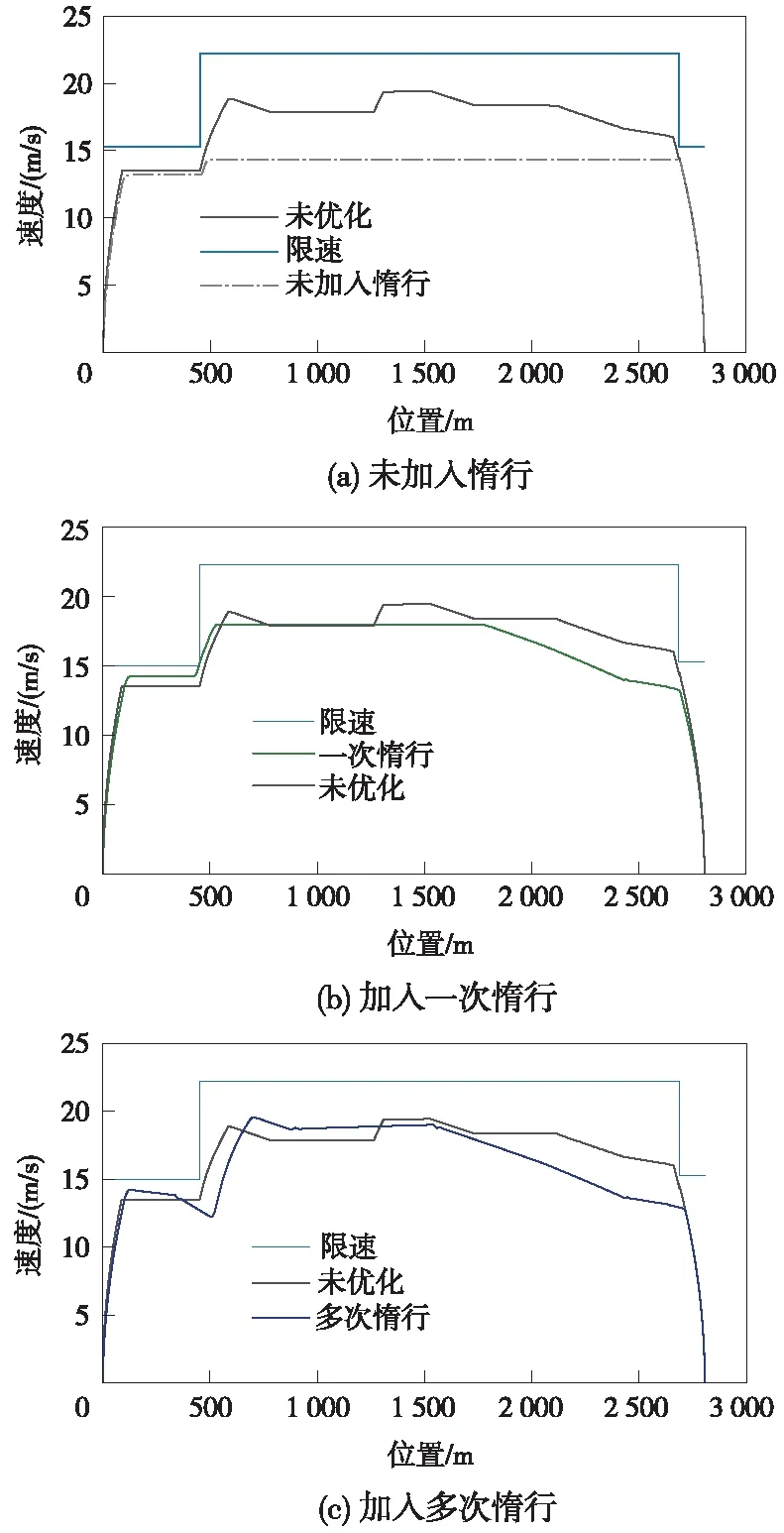
图6 不同策略下优化曲线
在满足列车准点要求的前提下,多次加入惰行的控制策略运行时间为190.3 s,能耗12.47 kW·h为3种驾驶策略中耗能最低,与策略未加入惰行相比节能18.3%,与策略加入一次惰行相比节能13.2%。综合以上仿真结果可以得出,策略加入多次惰行的节能准点的优化效果最好。
5 结论
针对城市轨道交通中列车速度曲线优化问题,建立了多质点列车模型,设计以降低牵引能耗和提高列车准点的多目标优化模型,采用AGA-MOPSO多目标优化算法对不同驾驶策略进行优化,生成一组能耗-时间Pareto解,且通过模糊隶属度函数进行筛选,获得最优运行方案,得出以下结论。
(1)多质点模型下附加阻力的变化更加符合实际情况,与单质点模型相比减小了列车在变坡点和变曲率点的附加阻力误差。
(2)对比传统PSO算法处理多目标问题,AGA-MOPSO多目标优化算法在解方案的多样性上优于PSO算法,优化得到的最优方案效果更好,在准点误差0.3s的同时,节能可达7.4%。同时,在最优解稳定性上也优于PSO算法。
(3)对于3种不同的驾驶策略,采用模糊隶属函数从Pareto解集中选出3种驾驶策略所对应的最优方案。对比可知,在满足列车准点的前提下,加入多次惰行控制的驾驶策略优化效果更好。
本次优化结果为地铁列车运行方案提供了一定思路,但只考虑了列车准点以及能耗两个目标变量,下一步研究可考虑加入舒适度、电分相等其他因素。
