基于刚柔耦合模型的构架疲劳强度计算方法研究

罗志翔，郭冰彬，刘晓波，李 超，何辉永

（中车株洲电力机车有限公司大功率交流传动电力机车系统集成国家重点实验室，湖南 株洲 412001）

0 引言

随着轨道车辆运营速度的不断提高，车辆轮轨之间的动载荷不断增大，转向架各部件振动强度随之不断加剧[1]。虽然转向架拥有一系列悬挂装置，能够隔离轮轨之间的高频作用力，但由于轨道不平顺的随机性、轨道条件与轮轨接触状态随着运行时间在不断发生变化，这进一步增加了构架承载的复杂性，导致构架发生疲劳裂纹的事件时有发生[2]。目前铁道车辆强度试验标准主要参考：EN 12663-1：2010《铁路应用铁道机车车辆结构要求 第1 部分：机车和客车（货车的替代方法）》、TB/T 1335-1996《铁道车辆强度设计及试验鉴定规范》、VDV 152《符合BOStrab 规定的公共客运轨道车辆的结构要求》等标准，这些标准规定的恒幅载荷情况都是基于无限寿命设计理念的，且基于恒幅设计载荷谱将静强度计算结果应用于疲劳强度分析中，却没有考虑车辆实际运行时线路条件和轨道条件变化所引起的载荷的不确定性，虽然计算方法简单，但往往会导致设计强度不足。为了准确评估轨道车辆构架疲劳强度，本文提出了一种构架疲劳强度计算方法，能够考虑车辆运行时的真实情况，并以某构架为例，基于刚柔耦合动力学模型，采用动力学和有限元对该方法进行了应用。

1 刚柔耦合动力学理论

本研究采用Craig-Bampton 固定界面模态综合法[3]（简称C-B 法）模拟复杂的弹性体模型。其特征模态可由式（1）求出：

2 构架疲劳强度计算

2.1 构架疲劳强度计算评估流程

为了保证构架疲劳强度设计满足实际运用要求，本文提出了一种转向架构架有限寿计算方法，具体流程如图1 所示，主要包含以下几步：

图1 构架疲劳强度计算评估流程

（1）根据构架初始设计的三维实体模型，采用有限元理论建立考虑构架柔性的有限元模型。

（2）基于多体系统动力学理论，结合车辆、轨道系统结构参数，建立考虑构架柔性的车辆-轨道刚柔耦合系统动力学模型。

（3）基于车辆真实轨道不平顺激励谱、转向架激励以及车辆运行工况，通过车辆-轨道刚柔耦合系统动力学模型仿真计算获取构架关键部位全工况载荷特征。

（4）对关键部位载荷进行雨流循环计数，结合关键结构材料S-N 曲线，利用Miner 疲劳累积损伤理论，对构架进行疲劳强度计算。

（5）考虑一定的安全余量，将疲劳强度计算结果与设计寿命进行对比，若计算结果大于设计结果，则寿命设计完成，并进一步可考虑对构架进行轻量化设计，否则对构架重新进行设计，直至构架疲劳强度计算结果大于设计寿命。

2.2 弹性构架有限元模型建立

应用上述方法，以某轨道车辆构架为研究对象，根据构架的三维实体模型，采用大型三维绘图软件建立构架的三维几何模型，再将构架的三维模型导入有限元分析软中进行有限元建模，建模时注意考虑构架的细节特征。在有限元软件中将构架的有限元模型进行自由模态分析，模态频率一般考虑100 Hz 以上，通过计算发现该构架第一阶垂向弯曲模态频率为26.879 Hz，这符合文献[4]中描述的构架垂向振动加速度频率主要在0 ～ 30 Hz 之间，从而证明了构架有限元模型建立的准确性较高。借助于动力学软件UM与有限元软件的接口程序，采用Craig-Bampton 固定界面模态综合法将构架有限元模型转化为动力学模型中能够识别的构架弹性体模型。去除构架刚性模态频率，转换到动力学软件中的弹性构架模态频率与构架有限元自由模态频率误差最大不超过2%，如图2所示，说明弹性构架建立的较为准确，构架弹性体模型如图3 所示。

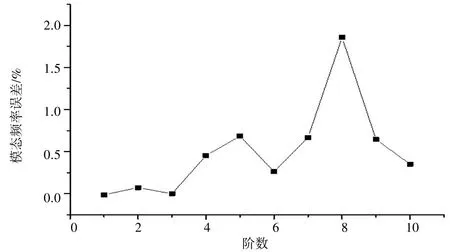
图2 构架转换前后模态频率误差

2.3 考虑构架弹性的车辆刚柔耦合模型建立

在动力学软件中采用自下而上的建模方法[5]，建立考虑一、二系和轴箱、车体为刚体，构架为弹性体的车辆刚柔耦合模型，如图4 所示。

为了提高仿真计算的精度和效率，将轨道模型中钢轨考虑为刚体，每个刚体分别拥有绕X轴转动和绕Y轴、Z轴平动的三个自由度。轨道激励为秦沈客运专线真实不平顺激励谱，其不平顺值幅值随运营里程见文献[5]。

2.4 构架动应力仿真计算

基于上述建立的刚柔耦合系统动力学模型，在动力学仿真过程中应用Craig-Bampton 固定界面模态综合法输出模型的动态应力。考虑车辆运行时的真实轨道路线，由于列车在曲线运行工况下比直线振动更加剧烈，这里主要考虑曲线工况。工况设置包含直线300 m、曲线半径400 m、2 段缓和曲线长度各150 m、圆曲线长度200 m、曲线超高100 mm，共计800 m，车辆运行时速80 km/h。选取典型位置A、B、C 三点分析其应力变化情况，其中，A 点节点号903081、B 点节点号907682、C 点节点号910019，各个位置如图5、图6、图7 所示，分别代表端部构架、一系簧连接构架处、中部构架位置处。

图5 A 点应力随时间变化曲线

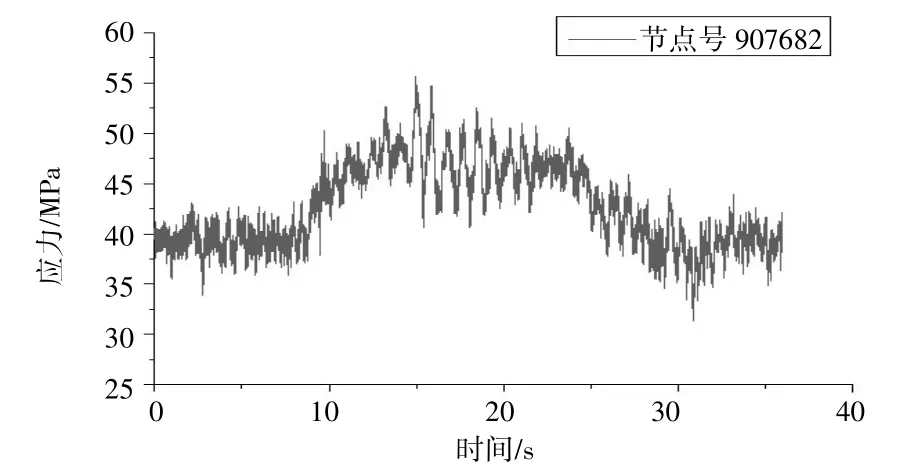
图6 B 点应力随时间变化曲线

图7 C 点应力随时间变化曲线

由图6 可知，各点的应力随运行里程的变化波动较大，这主要是因为曲线工况对构架的影响比较大。A、B、C 三点最大应力分别为23.9 MPa、55.7 MPa、27.2 MPa，应力水平均较小。由于构架中部C 点位置弹性被激发，导致其应力大于端部构架A 点应力；一系簧连接构架B 点处要大于C 点应力，这是由于前者直接与轮对通过一系簧连接，振动更大，这与实际情况也比较相符。

2.5 构架疲劳强度计算

车辆在实际运行过程中，承受的主要是随机载荷，不能将常幅试验下获取的材料S-N 曲线直接用于结构疲劳计算，本文基于Miner 线性累积损伤理论计算构架的疲劳损伤D：

考虑到应力的真实情况，采用Goodman 算式进行修正[6]。在动力学软件UM 的疲劳处理模块中，能够根据构架关注位置的载荷情况，结合材料的S-N 曲线，对构架进行疲劳计算。假设一年365 天，车辆每天运行20 h，应用该疲劳处理程序，通过仿真计算得到，该构架最危险位置在B 点附近，该处每天的损伤度为5.8e-5，如图8 所示，设计寿命为47 年。

图8 最危险位置每天的损伤度

3 结语

本文提出了一种构架疲劳强度计算方法，该方法是基于一种有限寿命设计思路，不仅能够考虑车辆实际运行时线路条件和轨道条件变化所引起的载荷的不确定性，而且能够计算出构架运营的年限，进而可考虑对构架进行轻量化设计；以某构架为例，建立了考虑构架弹性的刚柔耦合系统动力学模型，应用上述方法进行了服役情况下的寿命评估，能够表征构架在服役过程中的危险位置及其寿命，验证了本文提出方法的可行性。