塔式起重机臂架的优化设计及瞬态响应分析

2022-09-06刘帝芳郑国穗郑建校张锦华

装备制造技术 2022年5期

刘帝芳，郑国穗，郑建校，张锦华

（1.陕西建设机械股份有限公司，陕西西安 710201 2. 西安建筑科技大学机电工程学院，陕西西安 710055）

0 引言

目前关于塔机臂架的传统优化设计方法研究甚少，针对塔式起重机臂架的分析计算中，传统静力计算方法依旧占主导地位，计算不够精确。本文采用ANSYS 软件建立塔机臂架的有限元模型，以塔机双吊点水平起重臂作为研究对象，根据臂架的工作特点和性能要求，提出了型钢规格优化的结构优化设计策略，建立臂架最轻的结构优化数学模型，通过高精度的计算表明优化后典型工况下臂架重量较优化前有较大的改善。同时利用ANSYS 软件的瞬态动力学分析模块对塔机在变幅工况中的应力与位移时间响应情况进行分析，研究变幅工况下塔机的振动特点与瞬态应力。最终得出优化设计和时间历程响应分析结果满足要求。

1 臂架有限元模型

通过分析图纸，根据模型简化的原则及QTZ125臂架的结构特点，对臂架进行简化。采用节点法建立有限元模型，如图1 所示。确定其单元类型，臂架BEAM188，拉杆LINK8，定义臂架上下弦杆以及腹杆梁单元截面尺寸见表1。

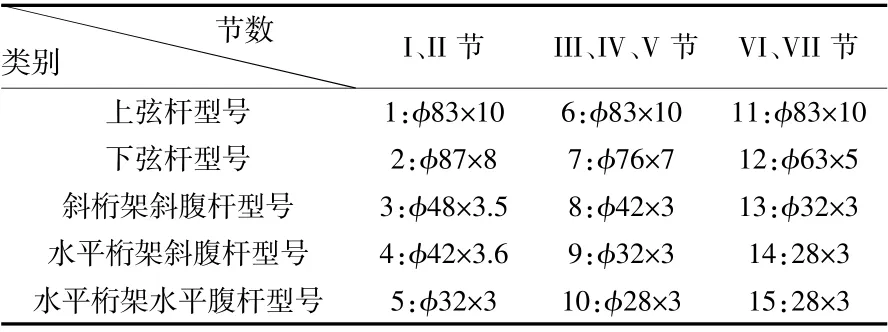
表1 QTZ125 塔式起重机吊臂型号的直径/mm

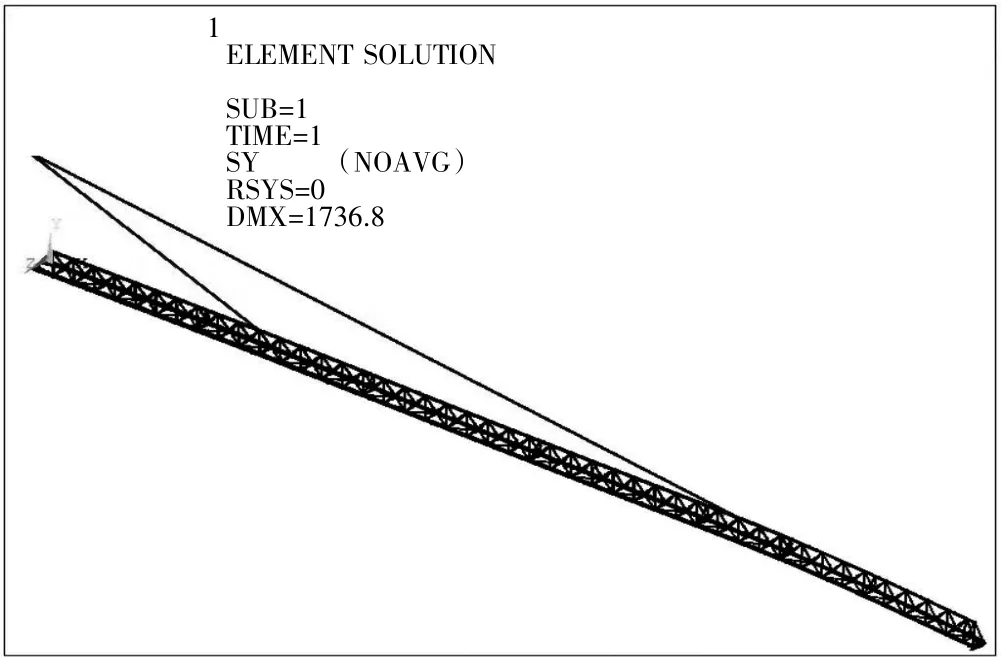
图1 臂架有限元模型

2 臂架优化设计

2.1 确定设计变量

在塔式起重机臂架的优化设计过程中，准确地确定设计变量，对目标函数的建立以及优化过程都显得尤为重要。本文提出的新优化模型的设计变量为结构中上下弦杆截面厚度或者为钢管的厚度，即:

Xi= {x1，x2，x3，x4，x5，x6，x7，x8}={R1，T2，R3，T4，R5，T6，T7，T8}

式中：R1为臂架第一和第二节上弦杆的内圆半径；T2为臂架第一和第二节下弦杆的截面厚度；R3为臂架第三、四、五节上弦杆截面内圆半径；T4，T7为臂架第三、四、五节下弦杆截面厚度；R5为臂架第六、七节上弦杆截面内圆半径；T6，T8为臂架第六、七节下弦杆截面厚度。

2.2 确定状态变量

（1）等效应力

其约束条件为：σmax≤[σ]，这是强度约束，σmax指的是每个梁单元的最大应力，即：

2.3 设定目标函数

本文提出的优化设计，其约束条件为强度约束和挠度约束。又由于本研究的优化目的是使结构自重最轻，因此新优化模型可以描述为：在满足结构强度、刚度的条件下使结构自重达到最轻。即:

2.4 荷载计算及求解

吊臂上作用的载荷有自重载荷、起升载荷、风载荷和水平惯性载荷。风载荷是作用在臂架上的风载荷和作用在重物上的风载荷的总和，根据小车在不同位置，吊重不同，作用在重物上的风载荷也不同。

（1）自重载荷：自重载荷指除起升载荷外起重机各部分的总重量。自重载荷属于惯性载荷，通过前面已经定义的密度，再定义重力加速度即可计算自重。

（2）起升载荷：起升载荷指起升质量的重力。起升质量离地起升或下降制动时，对承载结构和传动结构将产生附加的动载荷作用，在此取起升动载系数φ2= 1.25。通过起重特性曲线求出在56 m 处的吊重，标定：56 m 处起重量为2050 kg，即考虑小车质量Ge=162 kg ，吊具质量q= 127kg

式中，m为每节吊臂的质量，δ为启动时吊臂的回转角加速度，x为每节吊臂重心到回转中心的距离，n为吊臂回转时的角加速度，t为吊臂回转时启动加速度。

经计算得到各节水平惯性载荷数值，见表2。在施加完载荷之后进行求解。优化结果见表3。

表2 各节水平惯性载荷

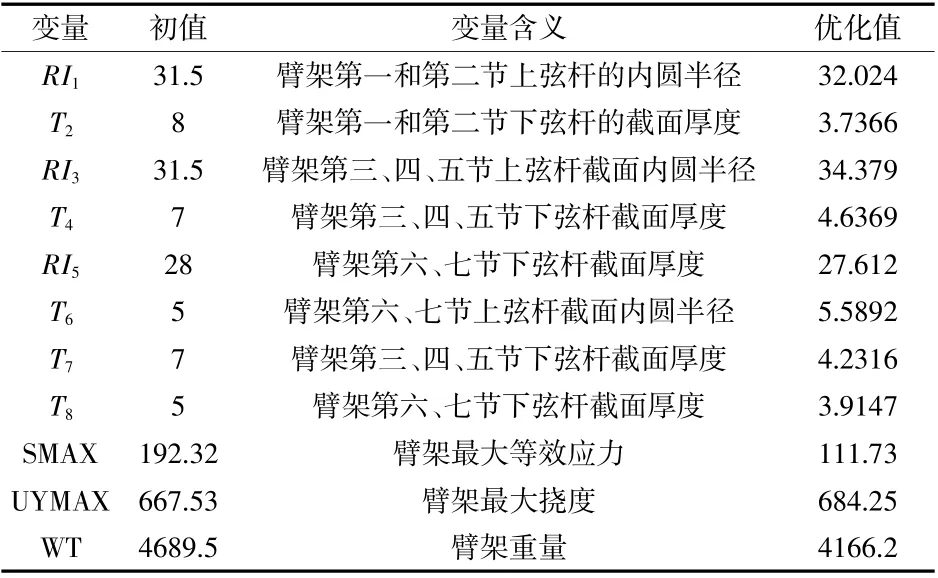
表3 设计变量初值与优化值

优化前后起重臂的结构及应力变形的状态为进行优化后起重臂满足状态变量要求的最佳结构尺寸参数，其最大应力和最大挠度都在许用范围内。优化结果显示，臂架的重量比未优化前减少了约11%，而臂架的应力为111.73 MPa，还在许用应力230 MPa范围之内。优化后，挠度变为684.25 mm，比原未优化前有所增加了，但是仍小于1778 mm，故优化结果符合要求，且优化效果较为明显，优化后应力云图（图2）。

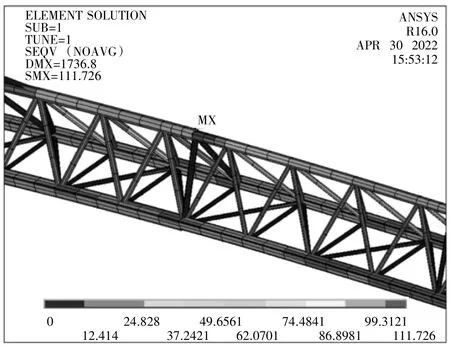
图2 最优结果的von Mises 应力云图

3 QTZ125 塔式起重机臂架瞬态动力学分析

塔机在实际工作中很少受到纯静态载荷，在多数工况中，塔机受静态、动态载荷的组合形式，很显然，对塔式起重机进行动态分析，探索并掌握其在动载荷作用下位移及应力随时间变化的情况，更接近于实际工况，具有重要意义。

3.1 求解方法及工况的确定

ANSYS 瞬态动力学分析提供了3 种求解方法，即：完全法（Full）、缩减法（Reduced）和模态叠加法（Mode Superposition）。其中，完全法采用完整的系统矩阵求解瞬态响应，在3 种方法中求解效果最好，功能最强大，可以包含各种材料与结构的非线性特征。本次使用功能最强大的完全法对QTZ125 塔机臂架进行瞬态求解。

本次研究只对QTZ125 塔式起重机的变幅工况进行动力学讨论。QTZ125 塔式起重机的最大幅度为56 m，最小幅度为3 m，在变幅工况中，选择起重量为8 t 和2.05 t，变幅区间为2.5 m ～ 50 m 的工况，研究塔机的变幅动力学。

3.2 施加荷载

起重小车和吊钩带动吊重在起重臂轨道上运动时，由于载荷的位置变化将对塔机结构产生动载荷作用，动载作用与小车的运行速度有关。当小车运行速度较小时，由于结构阻尼的存在，塔机的特性表现不明显，此时的结构可按静态进行力学分析。当小车运行速度较大时，塔机的动特性则会表现较为明显。

与动力学不同的是，当增加变幅载荷，取最大变幅速度作为载荷移动速度研究塔机的动力学过程。根据QTZ125 塔机的主要工作性能参数可知，塔机最大变幅速度为v= 60 m/min，即吊重以1 m/s 的速度在起重臂上移动。

时间历程响应分析与时间密切相关，变幅工况的载荷施加步骤如下：

（1）初始平稳载荷：施加自重、风载等静态载荷，载荷时间为60 s，施加载荷子步60 个，定义为载荷步1，使结构的应力和变形趋于平稳状态，达到静平衡状态。

（2）吊重变幅载荷首先根据吊重质量对变幅初始点进行载荷施加，载荷子步为10 个，定义为载荷步2，然后根据变幅速度，每隔1 s 将载荷依次移动625 mm，施加到各对应节点上，作为一个新的载荷步，载荷数目自2 开始逐次增加，每个载荷步中子步数均为10 个，每次定义新载荷步前将上一载荷步删除，以模拟小车变幅时载荷移动的效果。

3.3 QTZ125 塔式起重机瞬态动应力分析

利用塔式起重机臂架优化得到的新数据，修改钢结构的截面特性QTZ125 塔机吊重2.05 t 并由3 m变至56 m 工况各特征时刻结构应力云图见图3。

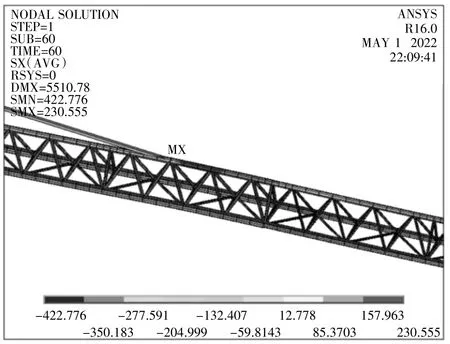
图3 Time=60s，幅度3m 臂架结构应力图

同理做出Time = 65 s，幅度10.0 m，Time = 81 s，幅度20.0 m，Time = 90 s，幅度40 m，Time = 95 s，幅度45 m，Time = 99 s，幅度50 m，4-35 Time =103 s，幅度56m 臂架结构应力图，可以看出，在变幅工况中，结构的最大应力是随着吊重载荷的移动而变化的，最大应力发生的区域大体上位于载荷作用位置附近，其值在130 ～ 230 MPa 之间变化，载荷的位置变化对结构的应力影响较大。与优化设计后所得到的应力云图相比，最大应力几乎保持不变，故可得出，在变幅工况下，变幅力对臂架的影响不甚明显。