广义多尺度集值决策系统最优尺度选择

胡 军 陈 艳 张清华 王国胤

1(计算智能重庆市重点实验室(重庆邮电大学) 重庆 400065)

2(重庆邮电大学计算机科学与技术学院 重庆 400065)

(hujun@cqupt.edu.cn)

在实际应用中，人们可能要在不同的粒度下对同一对象进行观察、表示、分析和决策，即对一个对象和某个属性，根据实际问题的不同粒度层次的需要，可取不同的值.针对上述多粒度描述的问题，Wu等人[1]提出了一种称为多尺度信息系统的知识表示系统.在多尺度信息系统中，一个对象根据不同的度量尺度，在每个属性上可以有多个不同取值，且不同尺度空间存在从细到粗的信息粒转换.多尺度广泛存在于地理空间分布、图像分析等多个研究领域[2-9].

目前，学者已经对多尺度信息系统进行了大量研究.Wu等人[1,10-11]介绍了多尺度决策系统的最优尺度选择方法及规则获取.从一致性角度考虑，Xu等人[12]及Wu等人[13-15]研究了多尺度决策系统的最优尺度选择方法.Hao等人[16]考虑到数据的动态变化，利用三支决策的方法研究了动态多尺度决策系统的最优尺度选择方法.铁文彦等人[17]讨论了对象动态更新情况下多粒度决策系统的最优粒度选择.顾沈明等人[18]定义了局部最优粒度，研究了多尺度决策系统的局部最优粒度和规则提取方法.Chen等人[19]为了简化最优尺度选择的计算过程，研究了基于矩阵的多尺度决策系统的最优尺度选择方法.以上研究假设多尺度信息系统中所有属性都具有相同尺度级数，Li等人[20]针对每个属性具有不同尺度级数的情况，定义了广义多尺度信息系统，并提出补充模型和格点模型来分析广义多尺度决策系统的最优尺度选择，此后又提出了基于属性重要度的逐步最优尺度选择方法[21].Wu等人[22]讨论了广义多尺度决策系统中几种最优尺度组合之间的关系.牛东苒等人[23]通过引入概率粗糙集，研究了可变精度下广义多尺度决策系统的最优尺度选择方法.Cheng等人[24-25]提出了基于序贯三支决策的最优尺度选择和属性约简方法.

文献[1-25]研究假设对象在属性各个尺度的取值都是唯一的，然而一些实际问题却不满足这一假设[26-31].为此，陈艳等人[32]提出了多尺度集值信息系统，给出了4种最优尺度选择方法，并讨论了在一致/不一致多尺度集值信息系统中它们之间的关系.该研究假设所有属性具有相同的尺度级数，使得属性只能在同一个尺度下进行组合.其次，最优尺度选择仅考虑决策系统的一致性或不确定性，忽略了实际应用中的代价问题，无法满足用户的个性化需求.

于是，针对不同属性具有不同数量的尺度及获取不同尺度数据的代价不同2个问题，本文对多尺度集值信息系统进行了扩展，提出具有代价的广义多尺度集值信息系统.在广义多尺度集值信息系统中，每个属性的尺度级数不同，在遍历每个属性的所有尺度时，针对尺度组合爆炸问题，提出了一种尺度空间更新方法，有效减少尺度空间中尺度组合数量；然后，综合考虑不确定性和代价2个因素的影响，提出了其最优尺度选择方法，可以快速地找到决策或分类结果最优且满足用户需求的尺度.

1 基本概念

本节主要介绍多尺度信息系统[1]及多尺度集值信息系统[32]的基本概念.

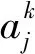
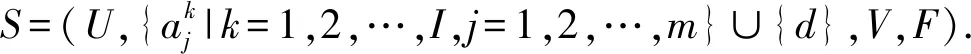
2 广义多尺度集值信息系统

本节主要给出广义多尺度集值信息系统的概念及相关性质，并讨论不同尺度组合下决策系统的不确定性和代价变化趋势.

2.1 广义多尺度集值信息系统

现有关于多尺度集值信息系统的研究假设每个属性的尺度级数都相同，然而实际问题中不同属性的尺度级数可能不同，因而需要对其做进一步推广.

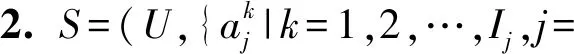
本文的研究基于集值的合取语义，即一个集值表示一个对象在某个属性下所有的值，并且它们都为真.

例1.表1是某行业关于供应商的信息调查与评价，其中U={x1,x2,…,x10}表示10个供应商，属性a1,a2,a3分别代表产品质量、配送效率和服务水平，且它们拥有不同的尺度级数，即I1=4,I2=3,I3=2，属性取值“E”“G”“F”“P”“B”“S”“M”“L”“Y”“N”分别表示“Excellent”“Good”“Fair”“Pass”“Bad”“Super”“Middle”“Low”“Yes”“No”[33].

Table 1 A Generalized Multi-Scale Set-Valued Information System表1 广义多尺度集值信息系统

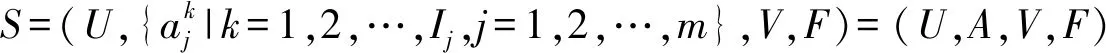
例2.在例1所示的广义多尺度集值信息系统中，其尺度空间ψ={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(2,1,2),(2,2,1),(1,2,2),(1,3,1),(4,1,1),(3,2,1),(3,1,2),(2,3,1),(2,2,2),(1,3,2),(4,2,1),(4,1,2),(3,3,1),(3,2,2),(2,3,2),(4,3,1),(4,2,2),(3,3,2),(4,3,2)}.

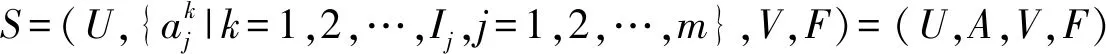
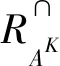
定义5.已知目标集合X⊆U，K是S的一个尺度组合，则X关于K的上、下近似集分别为

在尺度组合K下，通过上、下近似集，可将论域U划分为3个互不相交的区域，即正域、负域和边界域：

其中POSAK(X)表示一定属于X的对象集，NEGAK(X)表示一定不属于X的对象集，BNDAK(X)表示不能确定是否属于X的对象集.

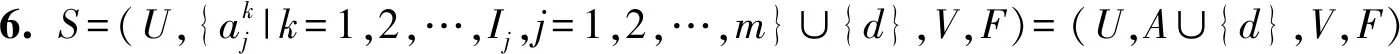
关于决策属性d的等价关系为Rd={(x,y)∈U×U|d(x)=d(y)}，则可将论域划分为U/Rd={D1,D2,…,Dr}，其中Dj,j=1,2,…,r表示不同的决策类.

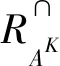
假设SK和SK′分别是广义多尺度集值决策系统S关于尺度组合K和K′的单尺度集值决策系统，且KK′.由定义7及可知，若单尺度集值决策系统SK是不一致的，则SK′也是不一致的；并且，若单尺度集值决策系统SK′是一致的，则SK也是一致的.

2.2 广义多尺度集值决策系统的不确定性

为了定量分析不同尺度下的不确定性，下面给出广义多尺度集值决策系统的不确定性度量.由于正域和负域的对象都是确定的，因此目标概念的不确定性仅来自边界域.于是，基于相似关系R，X⊆U关于尺度组合K的不确定性可以度量为[34]

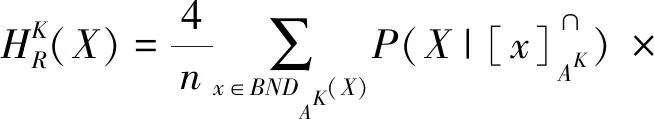
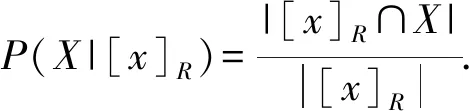
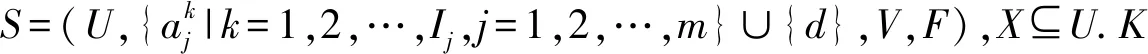
作文教学效率的高低在一定程度上决定着语文教学的成败。但提起写作文，却令不少师生感到为难。如何帮助学生突破写作瓶颈，让初中生爱上写作并写出好作文，进而提高写作水平呢？采取有效的作文教学策略是关键。

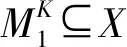
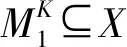
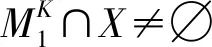
因此，若2个尺度组合满足KK′，则始终可以得到

证毕.

定理1表明，在广义多尺度集值决策系统中，尺度组合越粗，目标概念X的不确定性越大.

2.3 广义多尺度集值决策系统的代价

在决策过程中，不同尺度的数据，其测试代价往往不同，且对边界域对象进行延迟决策会产生延迟代价.本节主要讨论广义多尺度集值决策系统中的测试代价和延迟代价.

Table 2 A Generalized Multi-Scale Set-Valued Information System with Test Cost and Delay Cost表2 具有测试代价和延迟代价的广义多尺度集值决策系统

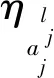
定义10.已知广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω)，X⊆U.X关于尺度组合K的延迟代价定义为

其中,BNDAK(X)是在尺度组合K下的边界域对象集，ωxi是关于xi延迟决策的代价，即决策系统SK的延迟代价为尺度组合K下边界域对象集延迟决策的代价.

定义11.在广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω)中，X⊆U.X关于尺度组合K的总代价为

COSTK(X)=TCK+DCK(X).

其中,TCK是在尺度组合K下获取所有对象属性值的测试代价，DCK(X)是在尺度组合K下边界域对象集的延迟代价.

定理2.已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟价的广义多尺度集值决策系统，X⊆U.K和K′是关于S的2个尺度组合，当KK′时，可以得到TCK≤TCK′.

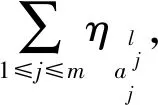
证毕.

定理3.已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟代价的广义多尺度集值决策系统，X⊆U.K和K′是关于S的2个尺度组合，当KK′时，可以得到DCK(X)≤DCK′(X).

证明.假设尺度组合K下边界域为E1,尺度组合K′下边界域为E2，当KK′时，X关于尺度组合K和K′的粗糙近似关系有及根据边界域定义可以得到E1⊆E2.因此，对于∀x∈BNDAK(X),始终满足x∈BNDAK′(X)，于是得到DCK(X)≤DCK′(X).

证毕.

可以看出，随着尺度组合变粗，其对应单尺度集值决策系统的延迟代价逐渐增大，测试代价逐渐减小，而总代价不具有单调性.

3 广义多尺度集值决策系统最优尺度选择

现有的最优尺度选择方法，大多是从决策系统的一致性或不确定性的角度出发，没有考虑到实际场景中的代价问题.因此，本节主要结合不确定性和代价，以用户需求为前提，找到决策或分类最优的尺度.

3.1 基于序贯三支决策的尺度空间更新

在广义多尺度集值决策系统中，当属性的尺度级数较大时，遍历每个属性的所有尺度将会导致尺度组合爆炸，计算成本较高.因此，这里基于序贯三支决策思想提出一种能有效减少一致性判断时间的尺度空间更新方法.

定义12.假设存在尺度组合K∈ψ，那么关于K的上、下边界定义为

UBψ(K)={K′|K′∈ψ,K′≻K}，
LBψ(K)={K′|K′∈ψ,K′K}.

其中,UBψ(K)表示尺度空间ψ中所有较K更粗的尺度组合，LBψ(K)表示尺度空间ψ中所有较K更细的尺度组合.

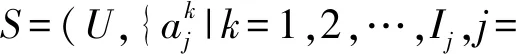
假设需进行一致性判断的尺度组合集合为UNC(ψ0)=ψ，其中ψ是S的初始尺度空间，第i-1次更新后决策结果分别为ACK(ψi-1)，REJ(ψi-1)，UNC(ψi-1)，则需进一步判断的尺度组合集合为ψi=UNC(ψi-1).通过引入序贯三支决策思想对UNC(ψi-1)中的尺度组合进行判断可得到第i次更新后尺度空间的决策结果分别为

ACK(ψi)={Ki}∪ACK(ψi-1)，
REJ(ψi)={Kj}∪UBψi(Kj)∪REJ(ψi-1)，
UNC(ψi)=ψi-ACK(ψi)-REJ(ψi).

其中,Ki是尺度空间第i层满足一致性的尺度组合，Kj是尺度空间第i层不满足一致性的尺度组合，UBψi(Kj)为尺度组合Kj的上边界，UNC(ψi)表示i次更新后需进行一致性判断的尺度组合.当UNC(ψi)=∅，可以得到S中所有一致的单尺度集值决策系统的尺度组合，即更新后的尺度空间ψ′=ACK(ψi).

因此，可得到尺度空间更新算法：

算法1.广义多尺度集值决策系统尺度空间更新.

输入：广义多尺度集值决策系统S=(U,A∪{d},V,F);

输出：更新后的尺度空间ψ′.

① 初始化ψ={K=(l1,l2,…,lm)|1≤lj≤Ij,j=1,2,…,m},ACK(ψ0)=∅,

REJ(ψ0)=∅,UNC(ψ0)=ψ,

ψi=UNC(ψi-1)(i≥1);

② whileUNC(ψi-1)≠∅ do

③ for eachK∈UNC(ψi-1) do

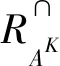
⑤ACK(ψi)←{K}∪ACK(ψi-1);

⑥ else

⑦REJ(ψi)←{K}∪UBψi(K)∪

REJ(ψi-1);

⑧ end if

⑨UNC(ψi)←UNC(ψi-1)-ACK(ψi)-REJ(ψi);

⑩i++;

算法1首先计算了广义多尺度集值决策系统的尺度空间，时间复杂度为O(I1×I2×…×Im).然后针对尺度空间中尺度组合对应的决策系统进行一致性判断，其中每个相似类的计算需要时间复杂度为O(m×|U|).在最坏情况下，假设所有尺度组合的决策系统都是一致的，需进行|ψ|=I1×I2×…×Im次判断，所以算法1总的时间复杂度为O(m×|U|×|ψ|).

下面举例说明尺度空间更新的计算过程.

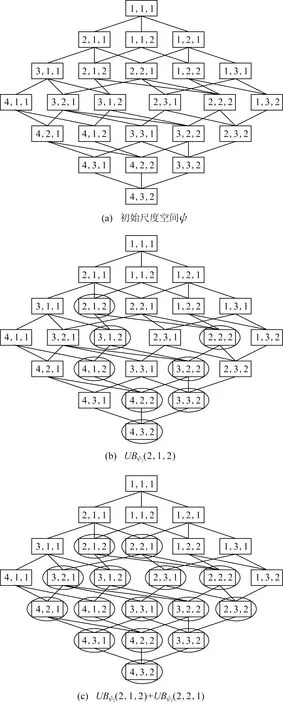
Fig. 1 The scale space of generalized multi-scaleset-valued decision system图1 广义多尺度集值决策系统的尺度空间

例3.根据例2可知，广义多尺度集值决策系统S的尺度空间如图1(a)所示.通过计算可以得到：

第1层关于尺度组合(1,1,1)的决策系统S(1,1,1)是一致的，则ACK(ψ0)={(1,1,1)}，REJ(ψ0)=∅，UNC(ψ0)=ψ-ACK(ψ0)=ψ1.

第2层尺度组合(2,1,1),(1,1,2),(1,2,1)是一致的，则ACK(ψ1)={(1,1,1),(2,1,1),(1,1,2),(1,2,1)},REJ(ψ1)=∅，UNC(ψ1)=ψ1-ACK(ψ1)=ψ2.

第3层尺度组合(3,1,1),(1,2,2),(1,3,1)是一致的，(2,1,2),(2,2,1)是不一致的.根据图1(b)(c)可知UBψ2(2,1,2)={(3,1,2),(2,2,2),(4,1,2),(3,2,2),(4,2,2),(3,3,2),(4,3,2)},UBψ2(2,2,1)={(3,2,1),(2,3,1),(2,2,2),(4,2,1),(3,3,1),(3,2,2),(2,3,2),(4,3,1),(4,2,2),(3,3,2),(4,3,2)},则ACK(ψ2)={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1)}，REJ(ψ2)={(2,1,2),(2,2,1)}，UNC(ψ2)=ψ2-ACK(ψ2)-REJ(ψ2)={(4,1,1),(1,3,2)}=ψ3.

第4层尺度组合(4,1,1),(1,3,2)是一致的，则ACK(ψ3)={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1),(4,1,1),(1,3,2)},REJ(ψ3)={(2,1,2),(2,2,1)},UNC(ψ3)=∅.

于是，更新的尺度空间ψ′=ACK(ψ3)={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1),(4,1,1),(1,3,2)}.

可以发现，广义多尺度集值决策系统的初始尺度空间|ψ|=I1×I2×I3=24，即需进行24次一致性判断，而更新后的尺度空间|ψ′|=9，且只需11次一致性判断即可得到所有一致的单尺度集值决策系统.因此，对于尺度级数较高的广义多尺度集值决策系统，该尺度空间更新方法能有效地提高计算效率.

3.2 最优尺度选择

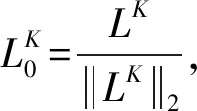
定义14.已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟代价的广义多尺度集值决策系统，X⊆U.那么，X关于尺度组合K的评价为

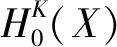
因此，在满足用户需求的情况下，以最小化不确定性和代价为目标建立最优尺度选择模型，具体为：

其中,Huser和Costuser分别是用户对于不确定性和代价的需求.

该模型以用户需求为约束条件，根据最小化评价来选择最优尺度.对于一个广义多尺度集值决策系统，有可能存在一组满足用户需求的可行解.由于该模型需要同时优化2个目标且目标之间存在冲突，即一个目标性能的提高是以牺牲另一个目标为代价的.例如，在满足约束条件可行的解决方案中，有些是低代价高不确定性的，有些是低不确定性高代价的.为此，通过引入理想解来计算可行解与理想解的差值，差值越小则表明越接近理想解，那么最接近理想解的尺度为最优尺度.

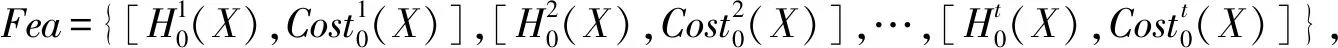
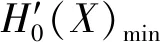
定义16.已知S=(U,A∪{d},V,F,η,ω)是一个具有测试代价和延迟代价的广义多尺度集值决策系统，基于加权的最优尺度选择模型为

其中,DifK表示加权差异程度，θ∈[0,1]表示加权系数.加权系数θ可根据用户需求进行设置，当θ=0时，该模型退化为基于代价的最优尺度选择；当θ=1时，该模型退化为基于不确定性的最优尺度选择.

因此，可以设计广义多尺度集值决策系统最优尺度选择算法为：

算法2.广义多尺度集值决策系统最优尺度选择.

输入：广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω)，Huser，Costuser，θ，X;

输出：最优尺度组合K′.

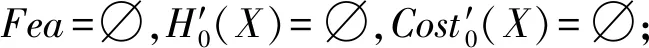
② 调用算法1更新尺度空间为ψ′；

③ for eachK∈ψ′ do

④ 得到POSAK(X),NEGAK(X),BNDAK(X)；

⑥ end for

⑦ for eachK∈ψ′ do

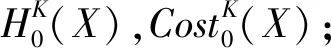
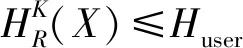
Costuserthen

在最坏情况下来分析算法2的时间复杂度，即假设每个对象都是一个独立于条件和决策属性的概念.在算法2中，步骤③～⑥在不同尺度下计算不确定性和代价，它的时间复杂度是O(|ψ′|×|U|2).步骤⑦～的目的是获取满足用户需求的可行解，时间复杂度为O(|ψ′|).在最坏的情况下，初始尺度空间ψ中的所有尺度组合K的单尺度集值决策系统SK都是一致的，即|ψ|=|ψ′|.根据分析可知，该算法的时间复杂度为O(|ψ|×|U|2).下面举例说明最优尺度选择的计算过程.

例4.在表2给出的具有测试代价和延迟代价的广义多尺度集值决策系统S=(U,A∪{d},V,F,η,ω)中U={x1,x2,…,x10},X={x1,x2,x3,x9,x10}，关于决策属性的论域划分结果为U/Rd={(x1,x3,x4,x7,x9),(x2,x5,x6,x8,x10)}.根据例3可知：更新的尺度空间ψ′={(1,1,1),(2,1,1),(1,1,2),(1,2,1),(3,1,1),(1,2,2),(1,3,1),(4,1,1),(1,3,2)}，其中BNDA(1,1,1)(X)=BNDA(2,1,1)(X)=BNDA(1,1,2)(X)=BNDA(1,2,1)(X)=BNDA(3,1,1)(X)=BNDA(1,3,1)(X)=BNDA(4,1,1)(X)={x6,x7,x9,x10}，BNDA(1,2,2)(X)=BNDA(1,3,2)(X)={x2,x6,x7,x9,x10}.根据定义14～16及归一化处理，其计算结果如表3所示，表3中粗体数据表明：在当前尺度组合下决策系统的不确定性或代价是最小的.当用户对不确定性和代价需求分别是Huser=0.4，Costuser=100时，根据最优尺度选择模型，可得到不确定性和代价最小的最优尺度组合是K=(4,1,1).

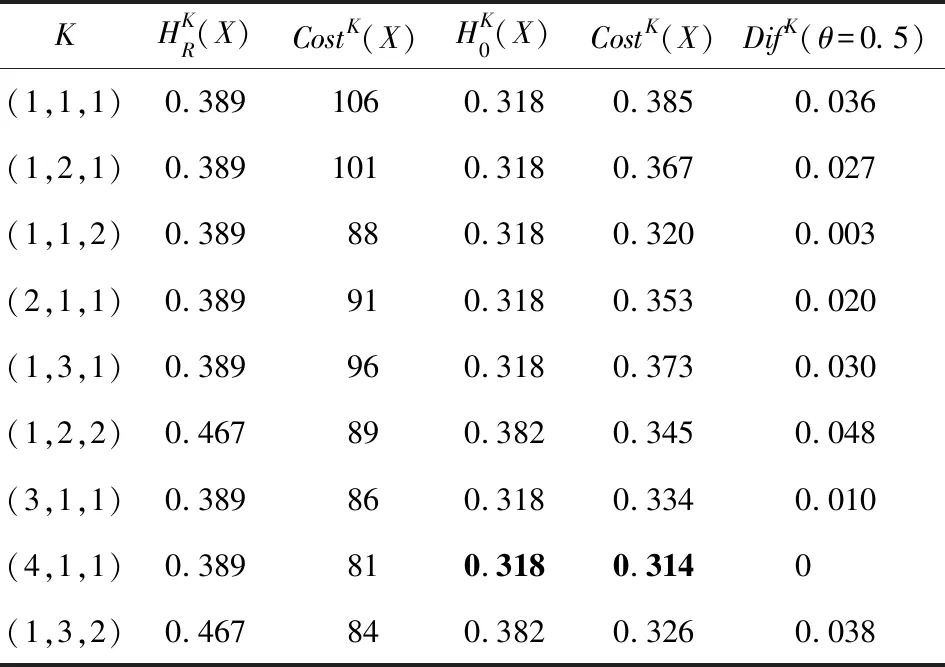
Table 3 The Results Based on Weighted Optimal ScaleSelection Model表3 基于加权的最优尺度选择模型计算结果

例4中，根据最优尺度选择模型可得到唯一的尺度组合解，但在有些广义多尺度集值决策系统中，根据最优尺度模型可能得到一组可行解.假设在例4模型中，满足用户需求的尺度组合为(1,1,2),(2,1,1),(1,3,1),(3,1,1),(4,1,1)，于是可以得到其理想解为Ide=[0.318,0.314].在基于加权的最优尺度选择模型中，假设用户给定的加权系数θ=0.5，可以计算出Dif(1,1,2)=0.003，Dif(2,1,1)=0.020，Dif(1,3,1)=0.030，Dif(3,1,1)=0.010，Dif(4,1,1)=0.因此，可以得到(4,1,1)是最优尺度组合.

例4说明算法2在得到唯一解或一组可行解情况下，其最优尺度选择的一致性.

4 实验结果与分析

为了验证本文提出的最优尺度选择算法的可行性和有效性，从UCI数据库中选取了6个数据集进行数值模拟，其详细信息如表4所示.

为了满足实验要求，本文参照文献[16]中提出的方法构造多尺度决策系统.具体而言，首先对条件属性进行扩展.若条件属性值为离散型，则尽量对属性值进行合并，保证其不重复；若条件属性值为连续型，则将属性值划分为多个区间，并将每个区间看作一个属性值.然后，随机丢失部分数据值，其取值为该属性相应尺度下的值域，即可得到广义多尺度集值决策系统.表5列出了经过预处理后数据集的信息.

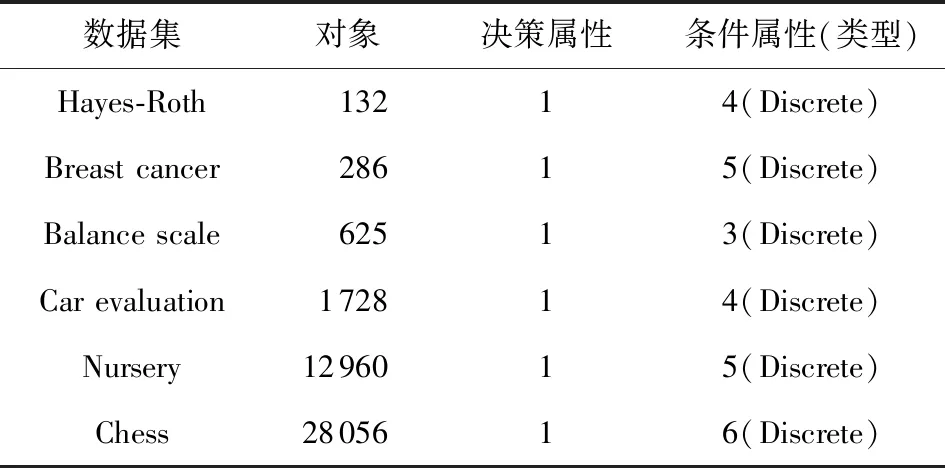
Table 4 The Original Dataset Information表4 原始数据集信息

Table 5 The Dataset Information after Preprocessing表5 预处理后的数据集信息

Table 6 The Related Cost Parameters of Datasets表6 数据集的相关代价参数

使用算法1对每个数据集进行尺度空间更新，结果如图2所示，其中横坐标表示数据集，纵坐标表示数据集的尺度组合数量.与LM(lattice mode)模型[20]相比，该尺度空间更新方法显著减少了尺度组合数量，从而可以减少决策系统一致性判断次数.

由于测试代价和延迟代价的变化趋势不同，总代价并不总是与不确定性的变化趋势相同，实验将不确定性和总代价进行归一化处理.如表7是6个数据集进行最优尺度选择的结果.

Fig. 2 The scale space update results图2 尺度空间更新结果

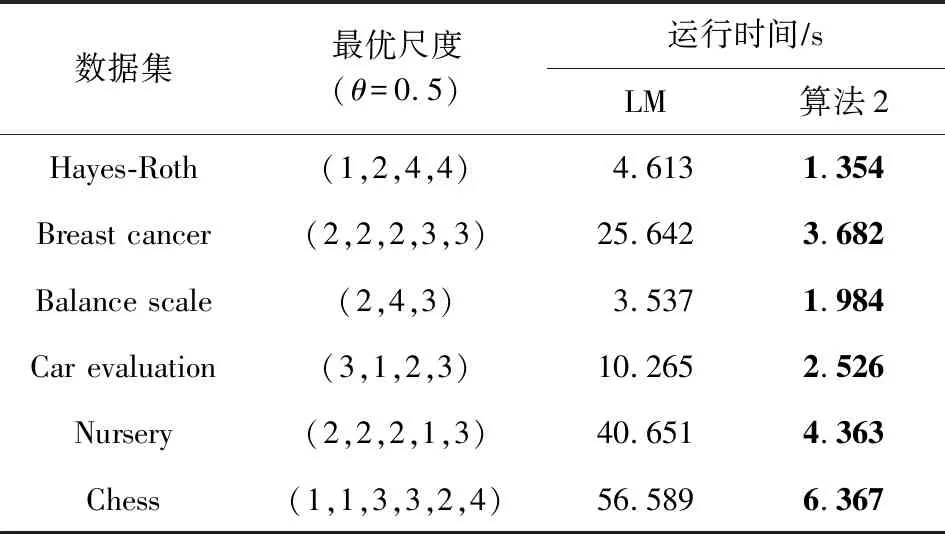
Table 7 The Optimal Scale Selection Results表7 最优尺度选择结果

为了分析不确定和代价对最优尺度选择的影响，本文分别在2组不同的参数下对Hayes-Roth数据集进行实验，其结果如图3和图4所示.在图3和图4中，横坐标代表更新尺度空间后决策系统的尺度组合数量，根据图2中的数据可知，经过尺度空间更新后，Hayes-Roth的尺度空间大小为64；纵坐标代表决策系统的不确定性或代价；曲线H表示不同尺度组合下决策系统的不确定性；曲线Cost表示不同尺度组合下决策系统的代价；曲线Dif表示在2种加权系数下，决策系统的不确定性和代价与理想解的差异程度.其中，在第1组参数下，测试代价和延迟代价都为1～10范围内的随机数，用户对不确定性和代价的需求分别为Huser=0.36和Costuser=300，其最优尺度组合为图3所标出的结果，即K=(1,2,4,4).在第2组参数下，测试代价和延迟代价都为1～15范围内的随机数，用户对不确定性和代价的需求分别为Huser=0.36和Costuser=600，其最优尺度组合为图4所标出的结果，即K=(1,1,4,4).可以发现，在2组不同的参数设定下，决策系统的不确定性和代价不同，但通过本文提出的方法均可得到满足用户需求的最优尺度.

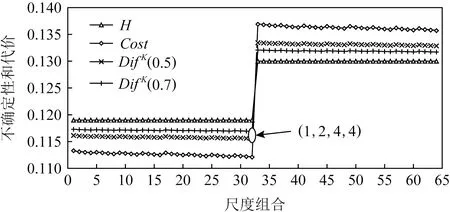
Fig. 3 The optimal scale of Hayes-Roth underthe first set of parameters图3 第1组参数下Hayes-Roth的最优尺度

Fig. 4 The optimal scale of Hayes-Roth under thesecond set of parameters图4 第2组参数下Hayes-Roth的最优尺度

5 总 结

本文主要研究了广义多尺度集值决策系统的最优尺度选择问题.首先，定义了广义多尺度集值决策系统的概念，并讨论了不同尺度组合下决策系统的不确定性和代价.然后，引入序贯三支决策思想对决策系统的尺度空间进行更新，减少了决策系统的一致性判断次数.在此基础上，提出了一种综合考虑不确定性和代价的最优尺度选择方法，并通过引入具有用户偏好的理想解对其进行优化.最后，通过实验证明该方法能够快速地得到一个满足用户需求的最优尺度.

作者贡献声明：胡军提出论文研究内容，并指导论文写作；陈艳负责研究内容的实现和论文写作；张清华、王国胤参与论文的研讨与修改.