隐私保护能力可调的节点定位协议
2022-09-06高振国王海军欧阳云
陈 岩 高振国 王海军 欧阳云 缑 锦
(华侨大学计算机科学与技术学院 福建厦门 361021)
(计算机视觉与机器学习福建省高校重点实验室(华侨大学) 福建厦门 361021)
(20013083005@stu.hqu.edu.cn)
随着物联网和第5代移动网络(5G)的空前发展,节点定位技术被广泛应用于家庭、工业、军事、医疗等领域[1-2].例如,厘米级精度的定位系统可以实现活动识别、行为模式发现、异常检测[3].节点定位是一种利用网络中锚点的位置信息来定位对象或设备的技术.使用这种技术,这些设备可以在任何地方获得它们的位置信息,例如室内、室外或没有全球定位系统(global position system, GPS)信号的区域.在信息提取过程中,估计实体(最终计算位置信息的设备)需要收集锚点的位置和与定位相关的测量值,例如接收信号强度、到达时间(time of arrival, TOA)、到达时间差(time difference of arrival, TDOA)和到达角度等.然而,这个过程可能会导致目标点和锚点的信息泄露.
节点定位期间的隐私保护至关重要.在军事上,可以通过向锚点发送定位请求来获取锚点的位置,精确摧毁锚点,进而摧毁整个网络[4].在生活中,用户在使用定位服务时不想暴露自己的位置,因为用户的个人隐私信息,如每日日程或健康状况,可以通过关联访问过的位置来推断[5-6].现有研究表明,在进行节点位置估计时,目标点和锚点都需要保护自己的隐私信息.
节点定位中保护隐私信息的方法大致分为3类:基于加密的方法、差分隐私方法、信息隐藏方法[7].加密技术[8-11]可以有效实现隐私保护,但计算量大,缩短了节点的使用寿命.差分隐私方法[12-17]计算效率高,然而,额外的噪声会降低定位精度.更轻量级的信息隐藏技术[18-22],如隐私保护求和(privacy-preserving summation, PPS)算法,计算高效,并且因为添加的噪声之和为零,在后续的计算过程中全部噪声将被抵消,定位精度也比较优秀.因此,PPS在节点定位中有着广阔的应用前景.然而,PPS和基于PPS的定位协议仍有一些问题需要解决:1)PPS需要生成和传输大量的干扰矩阵;2)评估PPS类算法隐私保护能力的指标受隐私信息中元素数量等无关变量的影响;3)文献[20]的上行链路到达时差隐私保护定位(uplink time difference of arrival privacy-preserving localization, UTDOA-PPL)存在冗余计算.
受已有研究的启发,本文旨在解决上述3个问题:
1) 为解决PPS算法通信量过大的问题,我们通过限制参与生成干扰矩阵的节点数量来调整通信量.在节点协同发送隐私信息时,不再要求节点组中所有节点共同参与生成干扰矩阵,而是从中随机选择k个节点为整组节点生成干扰矩阵.我们将这种算法命名为k型隐私保护求和(privacy-preserving summation withk, PPS-k)算法.后续内容证明了PPS-k算法在保护隐私信息上的有效性.
2) 为消除无关变量对PPS类算法评估结果的影响,提出了新的评估标准“隐私保护率”,即利用一组节点在估计另一组节点隐私信息时所缺少的方程数与隐私信息中未知量的个数之比作为评估标准.由于缺少的方程数和未知量个数均为隐私信息中元素数量的正比例函数.因此,隐私保护率消除了元素数量对评估结果的影响,且评估结果具有明确的取值范围.
3) 为消除UTDOA-PPL协议中存在的冗余计算,本文将PPS-k算法应用于TDOA定位,提出了新的隐私保护定位协议PPP-AMT(privacy-preserving protocol for anchor-measured TDOA).在消除了冗余计算的同时,PPS-k提高了节点间通信的灵活程度.
本文的贡献总结有3个方面:
1) 提出了PPS-k算法.该算法通过限制生成和传输干扰矩阵的节点数量为k来调整通信量,解决了PPS算法通信量过大的问题.通过理论分析证明了PPS-k算法在降低了通信量的同时,仍可实现隐藏隐私信息的功能.
2) 提出了隐私保护率指标.其定义为用于估计另一组节点隐私信息的额外方程数与隐私信息中未知量的个数之比.它突破了现有隐私保护能力评价指标的局限性,消除了与隐私保护能力无关的变量或属性对评估结果的影响,更合理有效地表征了PPS或基于PPS的协议的隐私保护能力.
3) 针对2种TDOA典型场景,基于PPS-k提出了2个定位协议,即PPP-AMT和PPP-TMT(privacy-preserving protocol for target-measured TDOA).在消除了冗余计算的同时,提高了定位时节点间通信的灵活程度.
1 相关工作
关于节点定位中保护隐私信息的研究工作一直在进行,现有的方法主要有基于加密的方法、差分隐私和信息隐藏3种.
1.1 基于加密的方法
将传输的信息通过某种规则或方法进行加密是隐私保护最常用的方案之一.文献[6]提出了隐私保护WiFi指纹定位方案(privacy-preserving WiFi fingerprint localization, PriWFL).该方案使用Paillier加密系统在保护了客户端位置信息的同时,也保证了服务端隐私数据的安全.文献[8]提出了TVM(temporal vector map)算法,该算法允许用户通过k匿名布隆(k-anonymity Bloom,kAB)过滤器和用于伪装定位请求的最佳邻居生成器在定位过程中保护用户隐私.文献[9]分析了文献[6]中PriWFL隐私保护方案的不足,提出了2种基于Paillier加密系统的WiFi指纹定位方案,在弥补了PriWFL方案缺点的基础上,保证了相同的定位精度.文献[10]将异步随机梯度下降应用于神经网络,并与同态加密相结合,保证用户的定位信息不会被泄露给服务器.同样,还有很多利用加密技术实现定位过程隐私保护的算法,如文献[11]等.
1.2 差分隐私的方法
差分隐私是针对数据库的隐私泄露问题提出的一种新的隐私定义,其主要通过使用随机噪声来确保查询请求的结果不会泄露个体的隐私信息.之后该方法被广泛应用到其他隐私保护算法中.
文献[13]将差分隐私引入WiFi指纹室内定位的在线定位阶段,设计了一种基于差分隐私保护的室内定位机制(differential privacy based privacy-preserving indoor localization mechanism, DP3),在隐私保护方面获得了优秀的效果.同样,文献[14]也提出了基于差分隐私的室内无线传感网络定位算法.文献[15]提出了一种差分隐私框架,其中包括定位隐私保护机制(location privacy preserving mechanism, LPPM)、基于定位的服务(location-based service, LBS)以及一个对手模型.利用该框架可以在提供定位服务的基础上,保证用户的位置信息安全.文献[16]提出了基于差分隐私的定位算法,在不提升通信次数和计算开销的情况下提升了定位精度和安全性.也有一些研究同时应用了差分隐私和加密算法,如文献[17]提出了一种利用同态加密和差分隐私保护的方案,以确保发布的数据不会泄露个人的位置信息.
1.3 基于信息隐藏的方法
信息隐藏技术将隐私信息隐藏在公开的信息中,使得入侵者不知道公开信息中是否隐藏了其他信息,同时也难以从公开信息中提取出隐藏的信息.
文献[18]通过超带宽(ultra wide band, UWB)传感器测量定位所需参数、目标节点计算位置信息的方式,实现了在定位过程中隐藏目标点位置信息的目的.文献[19]提出了基于PPS的相邻锚点间信息交互的相邻减法定位模型.文献[20]提出了一种隐私保护方案,该方案同样利用PPS算法,通过限制可用信息来隐藏目标点和锚点的位置.文献[21]通过隐私保护相邻乘积求和(privacy-preserving adjacent product summation, PPPS)和隐私保护相邻差值求和(privacy-preserving adjacent difference summation, PPDS)等信息隐藏算法来保护节点的位置信息.文献[22]针对水下传感网络,设计了基于PPS和PPDP(privacy-preserving diagonal product)的异步定位算法来隐藏位置信息.
信息隐藏相较于加密方案计算量小,对于能量严重受限的无线传感网络节点更加适用.与差分隐私方案相比,信息隐藏不会降低定位的精度,定位更加准确.因此我们认为信息隐藏是隐私保护中更加优秀的方法,具有广阔的应用前景.
2 理论基础
本节首先根据到达时差的存储位置定义了2种场景,接着简要介绍了TDOA定位法,最后阐述了传统PPS算法的具体内容.本文中常用的符号及其含义如表1所示:

Table 1 Symbol Definitions表1 符号及其含义
2.1 定位场景描述
设无线传感网络中一节点丢失了自身的位置信息.为重新确定自身位置,其向网络中的其他节点发送定位请求,并利用它们提供的信息计算自身的位置.像这样,丢失自身位置的节点根据网络中其他节点提供的信息计算自身位置的过程称为节点定位.在节点定位场景中,需要估计自身位置的节点为目标点,用T表示.提供定位所需信息的节点为锚点,锚点集合用A表示,其中第i个锚点表示为A(i),i=1,2,…,m.同时,令S表示网络中所有节点组成的节点集合,S={A,T}.节点定位技术有很多,例如TOA[23]和TDOA等,本文采用的是TDOA.
用ti表示锚点A(i)和目标点T之间信号单向传播的时间,用tj表示锚点A(j)和目标点T之间信号单向传播的时间,i,j=1,2,…,m,那么A(i)和A(j)之间的到达时差为
tij=ti-tj.
(1)
在实际应用中,一般选择其中1个锚点作为参考点,设参考点为A(m),其余锚点均以其为参考计算tim,i=1,2,…,m-1.
在不同的应用场景中,到达时差tim的存储位置也不同.设T的位置为x0=(x01,x02,…,x0n)T,其中n为位置信息的维度.A(i)的位置信息表示为xi=(xi1,xi2,…,xin)T,其中i=1,2,…,m.本文称图1中由锚点计算并存储tim的场景为AMT(anchor-measured TDOA)场景,称图2中由目标点计算并存储tim的场景为TMT(target-measured TDOA)场景.
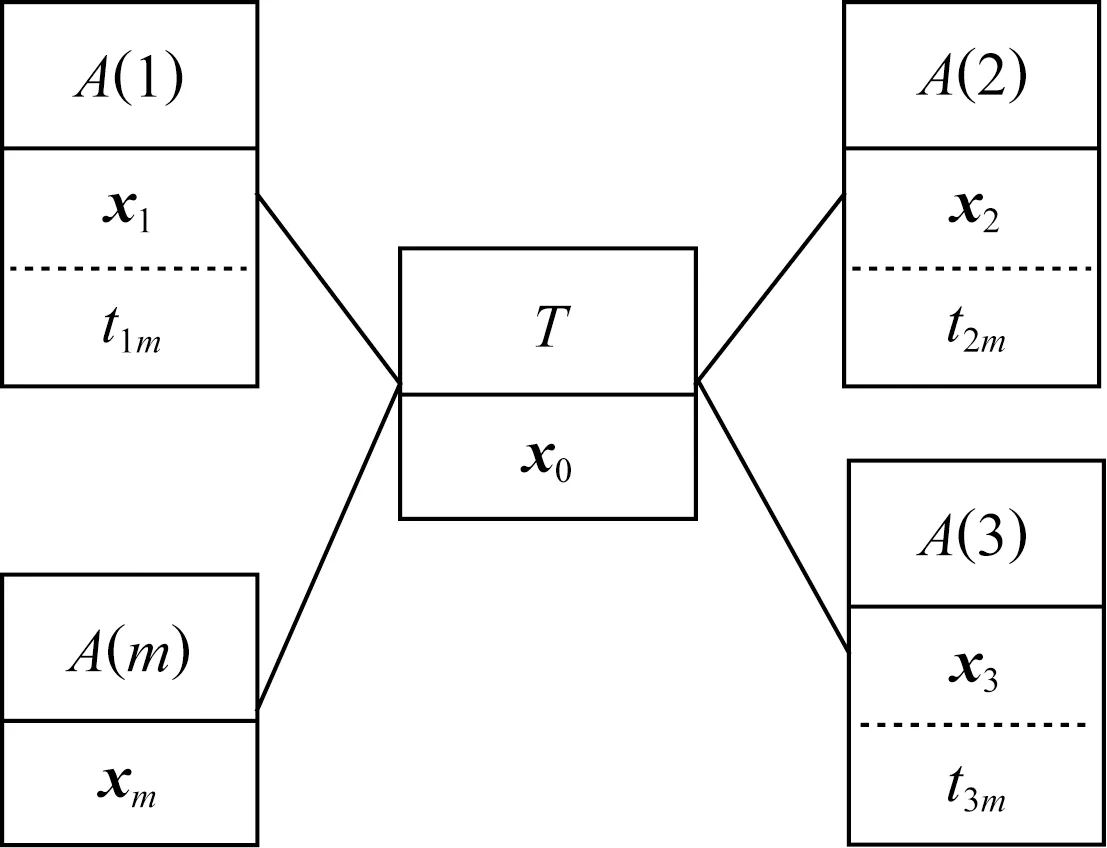
Fig. 1 AMT scenario where tim are stored in anchors图1 将tim存放在锚点中的AMT场景
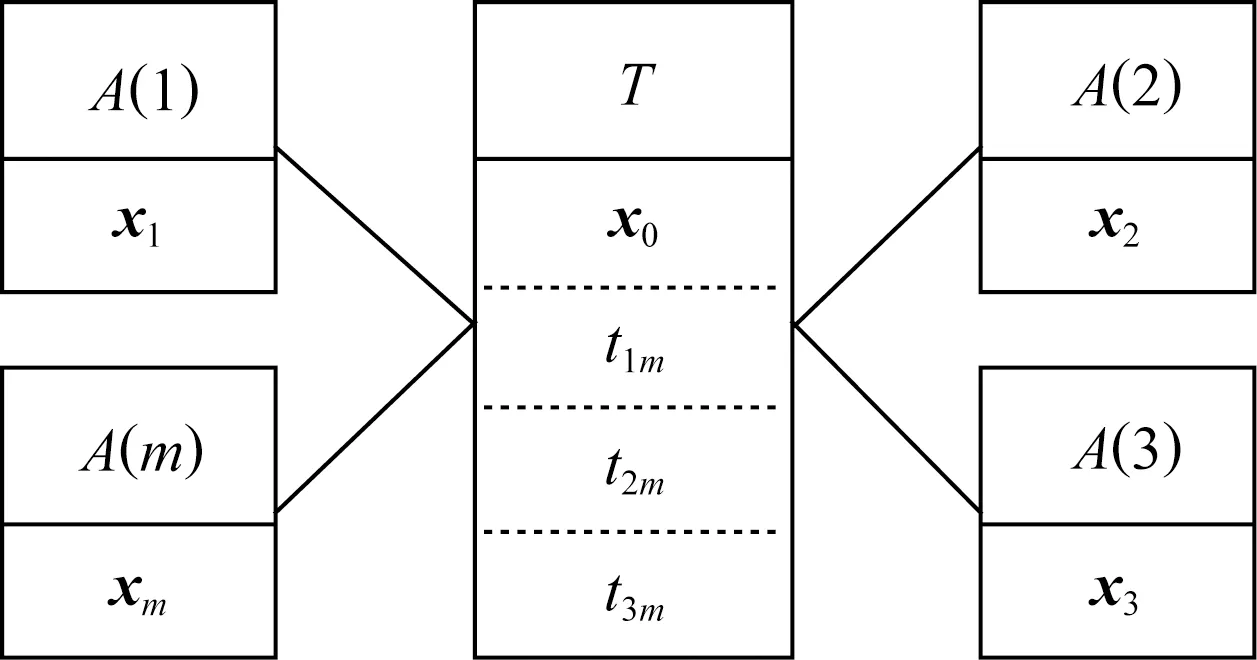
Fig. 2 TMT scenario where tim are stored in the target图2 将tim存放在目标点中的TMT场景
2.2 TDOA定位法
TDOA定位法一般将定位问题转换为超定线性系统的最小二乘估计问题[24-25].由于TDOA算法不是本文研究重点,这里直接给出结论,读者可以参考文献[20]学习具体的推导过程.
若用‖·‖表示·的模,那么T到A(i)的距离为di=‖xi-x0‖,T到A(m)的距离为dm=‖xm-x0‖.因此,距离差可以表示为dim=di-dm.利用时差信息,距离差dim也可以表示为dim=timc,其中c为电磁波传播的速度.最终,目标点位置可以通过

(2)
计算,其中
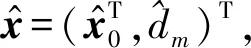
(3)
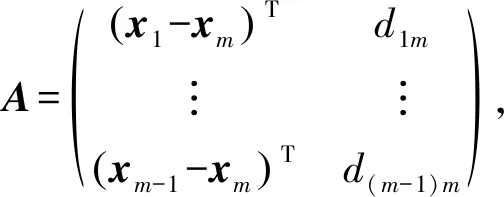
(4)
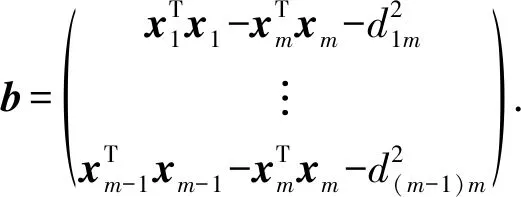
(5)
估计实体可以通过式(2)计算T的位置.根据本节的推导可知,估计实体可以得到xi和dim的值.如果T的位置由T本身计算,那么锚点的位置将暴露给T.若T的位置由锚点计算,T的位置将暴露给锚点.因此,TDOA定位中位置信息的泄露是不可避免的.在本文所研究的问题中,节点的隐私信息即为其位置信息,2种表述将在下文中交替使用.
2.3 传统的PPS算法
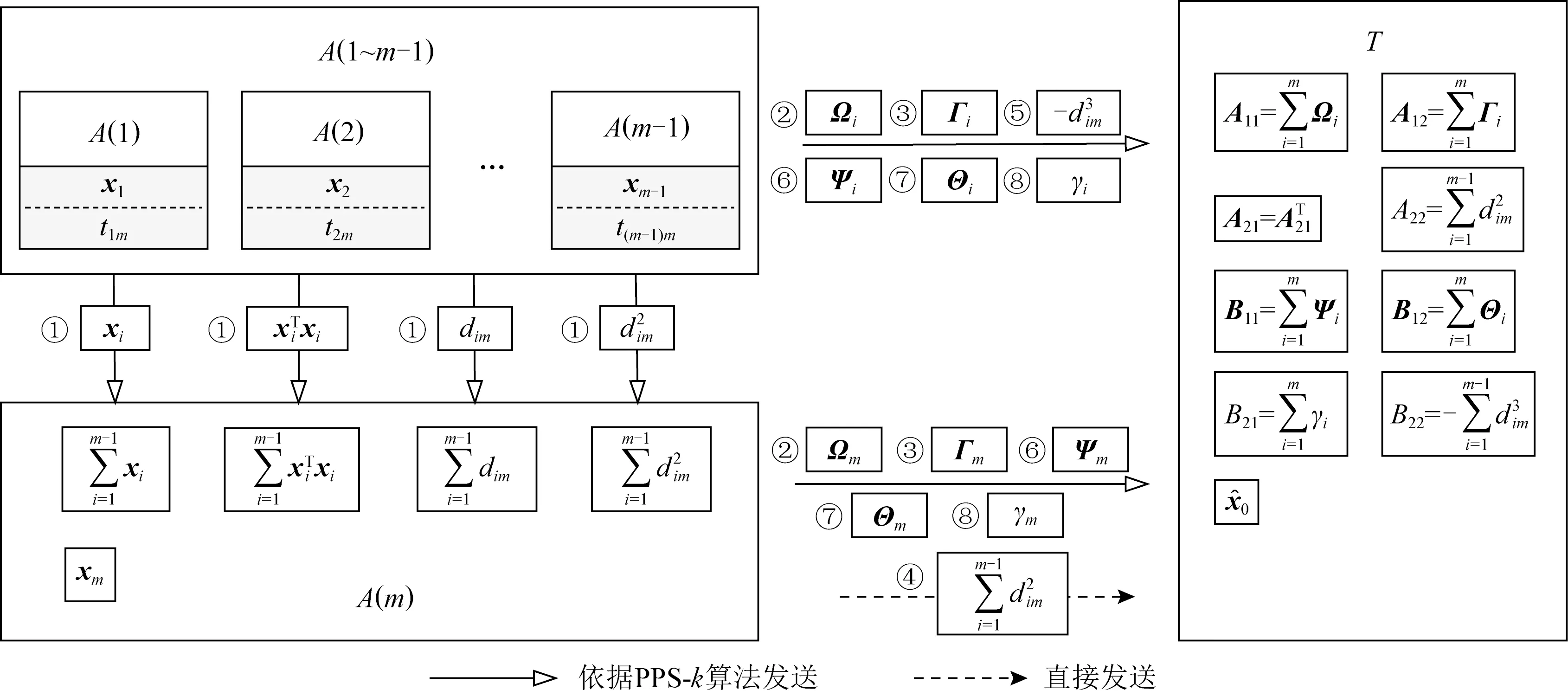
PPS是一种可以在保护各节点隐私信息的同时实现隐私信息求和的方法.假设A(i)持有隐私信息矩阵Xi∈n×1,i=1,2,…,m,T需要得到的值.为了保护隐私信息,A(i)不直接发送Xi,而是发送Xi与某干扰矩阵求和得到的值.图3展示了PPS算法的一个实例.
A(i)随机生成m个干扰矩阵且m个干扰矩阵的和为0矩阵.设这些矩阵为Wir∈保留其中的1个矩阵,然后将剩下的m-1个矩阵分发给其他m-1个锚点.每个锚点执行上述操作后,将收到的m-1个干扰矩阵与保留的1个干扰矩阵相加,得到最终用于隐藏信息的干扰矩阵Wi,i=1,2,…,m.
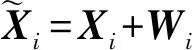

Fig. 3 The PPS process in a scenario with four nodes图3 当具有4个节点时PPS算法的工作过程
3 隐私保护评价标准
3.1 隐私保护率
文献[20]给出了一种评价隐私保护等级的定义:
定义1.Np级隐私.若一节点集Sc除了用已知信息构建的方程外,还需要额外构建Np个方程才能估计另一节点集Sp的隐私信息,那么称Sp能够对Sc保持Np级隐私.
当使用Np级隐私的概念评估PPS或PPS-k时,其评估结果不仅取决于算法本身,还取决于隐私信息的维度,也就是位置信息中元素的数量.但各元素之间是完全平行的,即没有联系,算法安全性不应受到信息中元素数量的影响.此外,该标准的评估结果没有确定的取值范围.因此,为了更合理、准确地评估隐私保护能力,提出定义2:
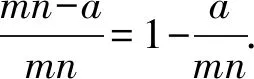
由定义2可知,隐私保护率也可以表述为“估计其他节点隐私信息所需要的额外方程数与隐私信息中未知量数之比”.隐私保护率的取值范围是[0,1],隐私保护率越大,算法或协议越安全.本文在分析隐私保护率时,假设节点之间不存在共谋,即节点的隐私信息不与任何其他节点共享.
3.2 通信量
通信量是指节点之间单向通信的次数.例如,A(1)向T发送信息,T成功接收到该信息,这个过程被称为1次通信.
为了方便计算,本文将产生的通信量归于发送信息的节点.对于上述例子,称A(1)产生1次通信.通信量直接关系着能量消耗与资源占用,通信量越少,能耗越低,若某协议的通信量较少,那么此协议是优秀的.
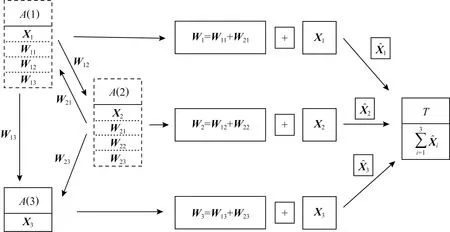
Fig. 4 The PPS-k process in a scenario with four nodes图4 当具有4个锚点时PPS-k算法的工作过程
本文采用诚实但好奇模型,其中所有节点都忠实地遵循设计好的协议,每个实体都对其他实体的隐私信息感到好奇,该模型与该领域的大多数研究一致[5].同时,假设节点之间的通信是安全的,并且隐私信息不会在通信链路上被窃听.该模型下的目标是保护锚点和目标点的隐私信息不泄露给其他节点,并且它们不能从对方那里获得隐私信息.
4 PPS-k算法
PPS实现了隐藏节点隐私信息的功能,但仍有不足:生成干扰矩阵的通信量大.该算法要求所有参与通信的m个锚点生成的干扰矩阵,此过程锚点间共通信m(m-1)次.因此,我们提出了PPS-k算法.通过改变生成干扰矩阵的锚点的数量调节锚点间的通信量,使其能够适应不同的应用场景.
4.1 算法内容
PPS-k通过选择系统中的部分锚点生成干扰矩阵,在降低锚点间通信量的同时,实现PPS算法的功能.本文将所有需要协同发送隐私信息Xi的m个锚点分为2类:被选中生成干扰矩阵的锚点为选中点,没被选中的锚点为参与点.设选中点数量为k,1≤k≤m,PPS-k具体执行流程如下:

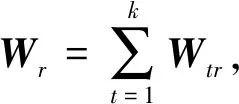
从PPS和PPS-k的概念中可知,PPS-k改变了Wi的组成.在PPS中,Wi由m个部分组成,例如,图4中的W1由W11,W21,W31组成.由于m是固定的,所以每次执行算法的通信量也是固定的.但是,在PPS-k中,Wi包含k个部分,锚点产生干扰矩阵的数量可以通过调整k来改变,特别地,在k=m时PPS-k可以退化为PPS.
4.2 k值对通信量的影响
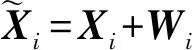
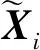

Fig. 5 The communication traffic versus k图5 通信量与k的关系
4.3 k值对隐私保护率的影响
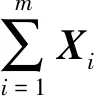
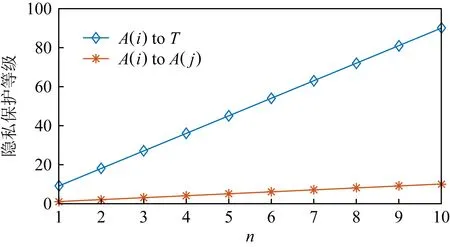
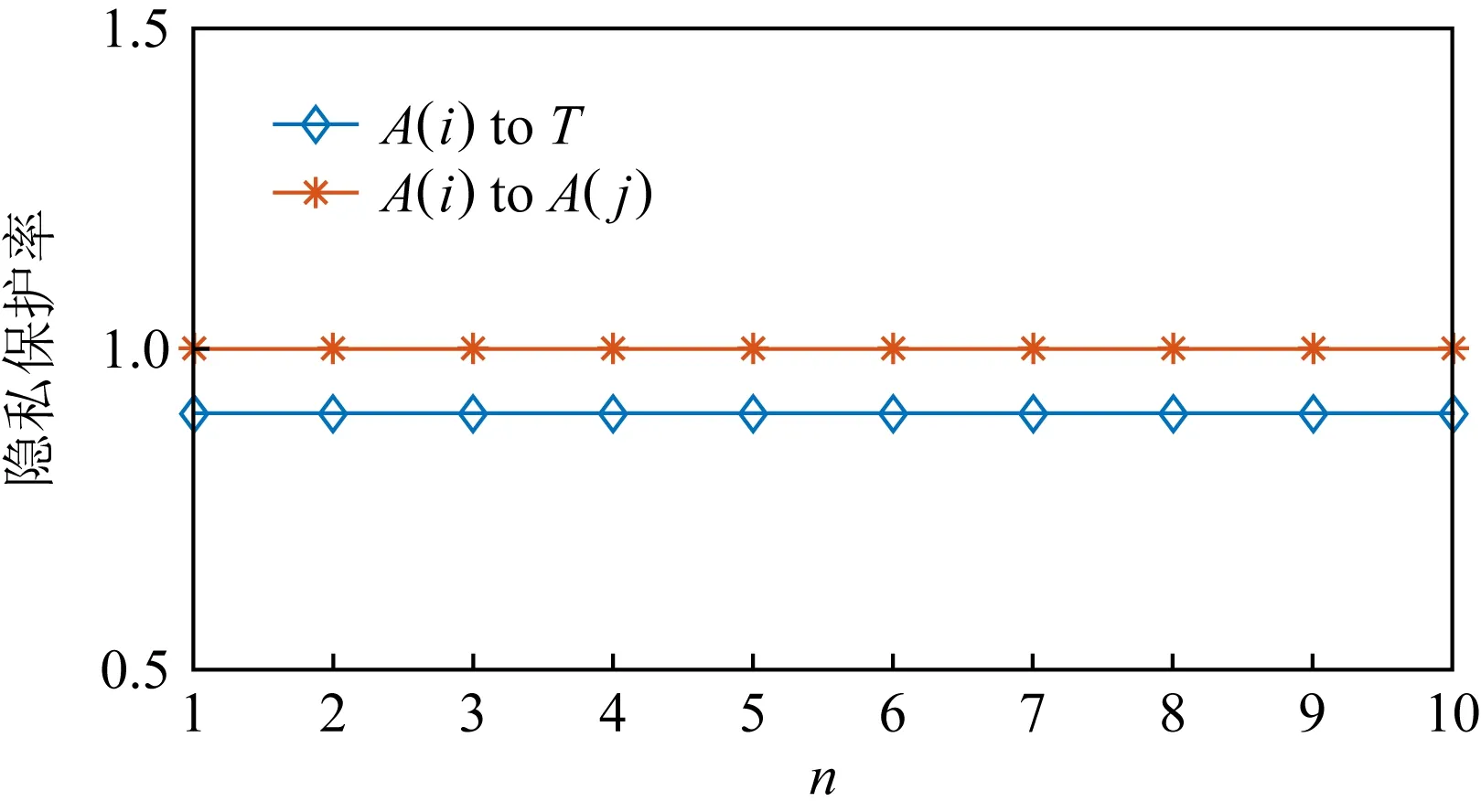
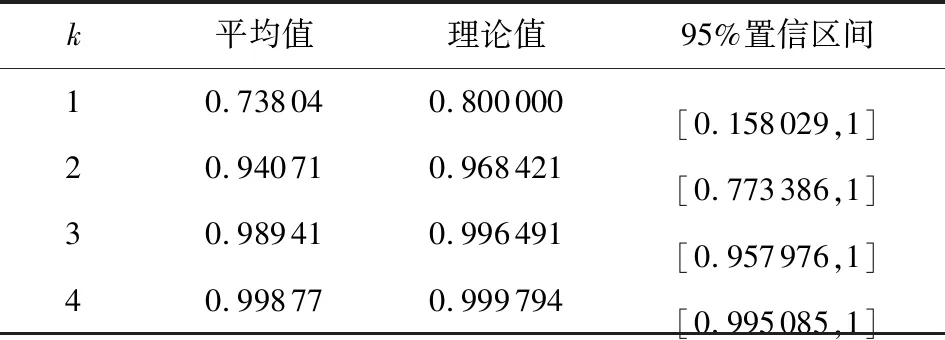
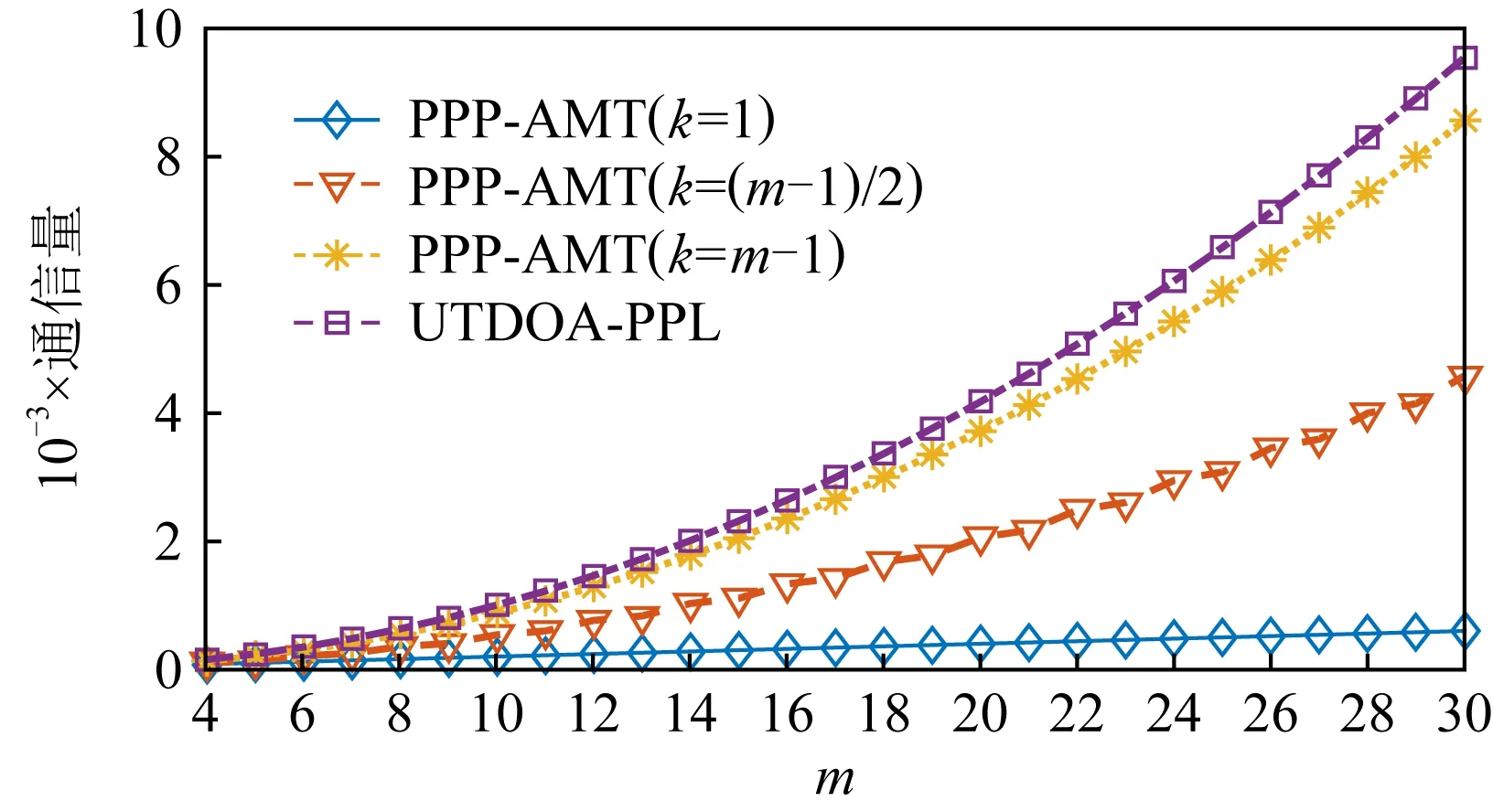
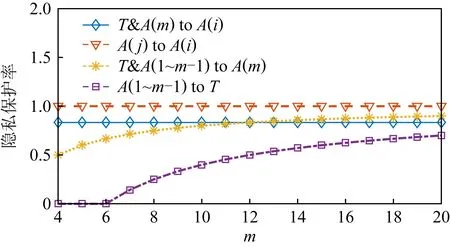
定理1.若Sc中节点共谋,且Sc中节点数为nc,其中1 1) 当T∉Sc时,非共谋节点可以保持1的隐私保护率. 4) 当T∈Sc,m=nc时,非共谋节点无法保护其隐私信息. 对于4),当T∈Sc,m=nc时,只有一个节点不参与共谋,该节点不能保护其隐私信息. 证毕. 由定理1中2)的证明可知,选中点全部被包含在Sc中的概率将随着k的增加而减小.当m和n固定时,增大k可以有效提高非共谋节点安全性.图6展示了当m=20且nc=10时,非共谋节点能够保护其隐私的概率与k的关系. Fig. 6 The probability of achieving privacy protection图6 实现隐私保护的概率 为了将PPS-k算法与TDOA算法相结合,实现节点定位过程中的隐私保护,需要将传统的TDOA算法重新设计.式(2)中ATA的计算结果根据参与运算的隐私信息需要划分为4部分:A11,A12,A21,A22,如式(6)所示.同样地,将ATb划分为B11,B12,B21,B22这4部分,如式(7)所示. (6) (7) 其中 (8) (9) (10) (11) (12) (13) (14) (15) 式(2)最终可以表示为 (16) T在进行定位时,需要分别计算A11,A12,A21,A22,B11,B12,B21,B22,最终利用式(16)求得自身位置.隐私保护定位协议设计的总体思路是通过PPS-k计算这些求和项,在不暴露每个锚点位置的情况下获得T的位置. 本节将PPS-k算法应用于具体的节点定位场景,分别针对AMT场景和TMT场景设计基于PPS-k算法的隐私保护定位协议. 针对时差信息tij存储在锚点中的AMT场景,本文提出了AMT场景的隐私保护协议(privacy-preserving protocol for AMT, PPP-AMT).在该协议中,PPS-k用于发送位置信息和与位置相关的测量值.当锚点发送位置信息时,它们发送有效信息和干扰矩阵的求和值.为方便陈述,只在协议的描述中显示有效信息,生成和发送干扰矩阵的过程隐含在语句“通过PPS-k”中,此外,协议的描述中有3种节点:A(i)(i=1,2,…,m-1)、参考点A(m)和T.图7展示了PPP-AMT的具体过程. 图7中的相关解释为: Fig. 7 The process of the PPP-AMT图7 PPP-AMT协议的工作过程 文献[20]利用PPS算法实现了TDOA定位中节点隐私保护,并针对AMT场景提出了UTDOA-PPL协议.接下来将分析比较UTDOA-PPL与PPP-AMT的通信量. 引理1.UTDOA-PPL协议,目标点T每次定位,节点间需通信11m2-12m+6次. 证明.UTDOA-PPL协议中,节点间的通信量主要包含3部分. 第1部分,A(i)根据PPS生成用于向A(m)发送定位所需信息的干扰矩阵,i=1,2,…,m-1.每次生成干扰矩阵锚点间需通信(m-2)(m-1)次.由于A(i)需要向T发送6个变量,因此第1部分共通信6(m-2)(m-1)次. 第2部分,所有锚点根据PPS生成用于向T发送定位所需信息的干扰矩阵.由于A(1~m)需要发送5个变量,因此共通信5(m-1)m次. 第3部分,A(1~m)向T发送定位所需相关信息产生的通信量.由于A(i)需要发送11个变量,A(m)需要发送5个变量,因此节点间需要通信11(m-1)+5次. 综合上述3部分,UTDOA-PPL协议每次定位节点间需通信11m2-12m+6次. 证毕. 在引理1的第1部分和第2部分中,需要发送隐私信息的锚点的数量分别为m-1和m.当PPS-k应用于AMT场景时,由于在PPS-k中只设置了唯一的k,k∈[1,m-1],因此,当PPS-k应用于定位协议时,不会完全退化成PPS,基于PPS-k的协议的通信量将总是低于基于PPS的协议的通信量. 引理2.PPP-AMT协议中目标点每次定位,节点间需要通信10km+10m-15k-4次. 证明. PPP-AMT协议中,节点间的通信量由3部分构成:第1部分,A(1~m-1)中选中点通过PPS-k生成干扰矩阵产生的通信量;第2部分,A(1~m)中选中点根据PPS-k生成干扰矩阵产生的通信量;第3部分,A(1~m)发送定位所需相关信息产生的通信量. 第2部分,选中点每次生成干扰矩阵需要通信k(m-1)次.因为需要发送5个矩阵变量,包括②中的Ω,③中的Γ,⑥中的Ψ,⑦中的Θ,⑧中的γ,所以生成干扰矩阵共通信5k(m-1)次. 第3部分,A(i)需要发送10个变量,A(m)需要发送6个变量,所以节点发送定位所需要的相关信息需要通信10(m-1)+6次. 综合上述3个部分,PPP-AMT协议中,T每次定位需要通信10km+10m-15k-4次. 证毕. 定理2.PPP-AMT能够实现如下隐私保护率: 证毕. 同样的方法可以容易地应用到TMT场景中.文献[20]中提出了基于TMT场景的TDOA隐私保护定位协议OTDOA-PPL,其中节点通过PPS相互通信.受其理论的启发,本文将OTDOA-PPL中的PPS通信算法改为PPS-k,并提出了TMT场景的隐私保护协议PPP-TMT.PPS-k赋予PPP-TMT更大的灵活性.由于PPP-TMT和OTDOA-PPL的理论基础是相同的,所以下面不详细阐述PPP-TMT的过程,而是直接给出结论,详情可以参考文献[20]的第5部分内容. 引理3.OTDOA-PPL协议中,T每次定位,节点间需要通信7m2-2m次. 引理4.PPP-TMT协议中,T每次定位,节点间需要通信7km-9k+9m-4次. 定理3.PPP-TMT能够实现如下的隐私保护率: 通过以上对于通信量的分析,不难得出定理4. 定理4.PPP-AMT和PPP-TMT的通信量分别小于UTDOA-PPL和OTDOA-PPL的通信量. 证明. 此证明可以分为2个子证明,分别证明PPP-AMT的通信量小于UTDOA-PPL的通信量和PPP-TMT的通信量小于OTDOA-PPL的通信量.第1个子证明为: 设UTDOA-PPL的通信量为 y1=11m2-12m+6, (17) PPP-AMT的通信量为 y2=10km+10m-15k-4, (18) 其中,m≥3,1≤k≤m-1.于是,原问题就转化为证明不等式 y1-y2>0. (19) 设 y(m,k)=y1-y2= (20) 式(20)对k求偏导得到 (21) 式(20)在m一定时,随k的增加单调递减.将k的最大值m-1带入式(20)得到 y(m,m-1)=m2+3m-5>0, (22) 其中,m≥3.于是式(19)得证,即PPP-AMT的通信量小于UTDOA-PPL的通信量.同理可证明PPP-TMT的通信量小于OTDOA-PPL的通信量. 证毕. 本节使用MATLAB模拟PPS-k算法,并比较隐私保护等级和隐私保护率的特征,还模拟了PPP-AMT和PPP-TMT,计算了它们的通信量和隐私保护率,最后分析了锚点数量和隐私信息维度对隐私保护率的影响. Fig. 8 The change in the privacy protection level图8 隐私保护等级的变化 首先利用4.2节中的场景,验证隐私保护率是否可以消除隐私信息维度n的影响.将节点数m设置为10,改变隐私信息维度n,观察在没有共谋的情况下隐私保护等级和隐私保护率的变化. 图8展示了Np隐私保护等级的变化,其中A(i)对T的隐私保护等级和所有锚点之间(即A(i)对A(j),j=1,2,…,m∧i≠j)的隐私保护等级随着n的增加而增加.图9给出了隐私保护率的变化.由图8、图9的结果表明,在评估算法安全性时,隐私保护率消除了隐私信息维数n的影响.因此,当评估隐私保护算法的保护能力时,隐私保护率比隐私保护等级更稳定、有效. Fig. 9 The change in the privacy protection rate图9 隐私保护率的变化 模拟了定理1的2).验证k值与实现隐私保护的概率之间的关系.设置m=20和nc=5,针对每个k值模拟100万次,如果锚点能够保护自己的隐私,输出为1;否则,输出为0.最后计算结果的均值,得到95%的置信区间.当置信区间的上限大于1时,记为1.结果如表2所示,实验结果的平均值与理论值一致. Table 2 The Probability of Achieving Privacy Protection表2 实现隐私保护的概率 Fig. 10 The traffic of PPP-AMT and UTDOA-PPL for varying the number of anchors图10 PPP-AMT和UTDOA-PPL锚点数量和通信量的关系 为了探究锚点数量对通信量的影响,设锚点数m=1,2,…,30,计算PPP-AMT和UTDOA-PPL的通信量,并分析通信量的变化.如图10所示,即使k取最大值,PPP-AMT的通信量也小于UTDOA-PPL的通信量.每次定位的通信量随着锚点数量的增加而增加.k值不同也导致通信量不同,k值越大,通信量越大. 采用同样的参数,对PPP-TMT和OTDOA-PPL进行模拟,结果如图11所示.我们可以得到同样的结论:即使k取最大值,PPP-TMT的通信量也小于OTDOA-PPL的通信量.锚点数相同时,k值和通信量正相关. Fig. 11 The traffic of PPP-TMT and OTDOA-PPL for varying the number of anchors图11 PPP-TMT和OTDOA-PPL锚点数量和通信量的关系 此外,我们模拟了PPP-AMT的隐私保护率.为了说明锚点数量m对隐私保护率的影响,将隐私信息维数n设置为3,计算不同锚点数量下的隐私保护率,其中m=4,5,…,20.结果如图12所示: Fig. 12 Privacy protection rate versus the number of anchors in the PPP-AMT图12 PPP-AMT中隐私保护率与锚点数量的关系 然后分析隐私信息维度n对隐私保护率的影响.将锚点数量m设置为10,并计算了在不同的n下PPP-AMT的隐私保护率.结果如图13所示: Fig. 13 Privacy protection rate versus the privacy dimension in the PPP-AMT图13 PPP-AMT中隐私保护率与隐私信息维度的关系 由图13可知,T连同A(m)对A(i)的隐私保护率和T连同A(1~m-1)对A(m)的隐私保护率随着隐私信息维度n的增加而增加.A(j)对A(i)的隐私保护率不受n的影响.A(1~m)对T的隐私保护率在开始时随着n的增加而增加,但当n>2时,其随着n的增加而降低. Fig. 14 Privacy protection rate versus the number of anchors in the PPP-TMT图14 PPP-TMT中隐私保护率与锚点数量的关系 Fig. 15 Privacy protection rate versus the privacy dimension in the PPP-TMT图15 PPP-TMT中隐私保护率与隐私信息维度的关系 本文提出了PPS-k算法,并将其应用于节点定位.通过调整k的值,基于PPS-k的协议比传统的基于PPS的协议更能满足实际应用场景的需求.因此,PPS-k算法具有更广阔的应用前景.为了评估基于PPS算法的技术的隐私保护能力,定义了隐私保护率的概念,消除了算法中隐私信息维度对评价结果的影响.未来的工作可以更多地研究PPS-k与特定隐私保护协议的集成.例如,每次发送新信息时重新定义k,而不是在整个定位过程中只使用相同的k. 作者贡献声明:陈岩和高振国负责本文研究方案和实验的设计,以及论文主体的写作;王海军和欧阳云负责实验的执行和论文的修改;缑锦参与研究方案的设计、实验数据分析以及论文的修改.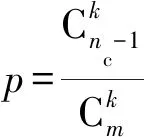
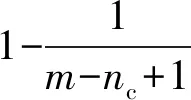
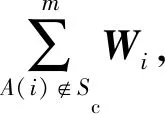
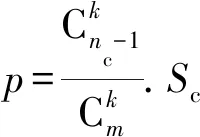
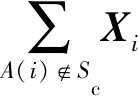

4.4 PPS-k算法与TDOA算法的结合

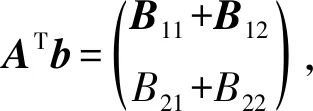
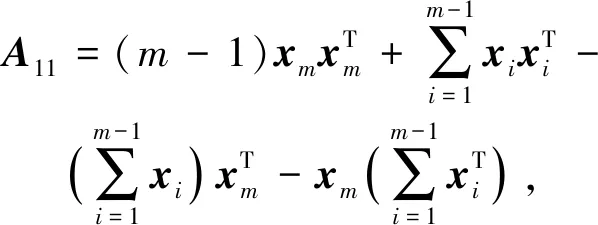
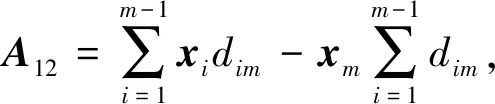

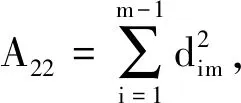
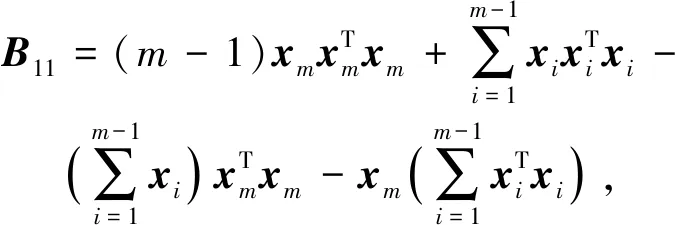



5 节点定位协议的设计与分析
5.1 AMT场景的隐私保护协议

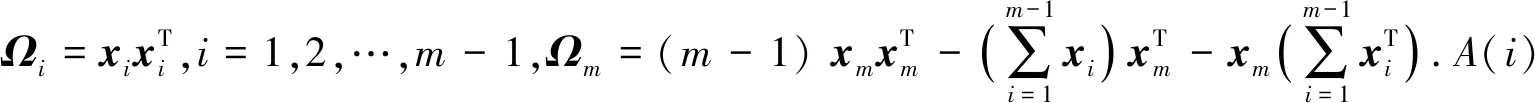
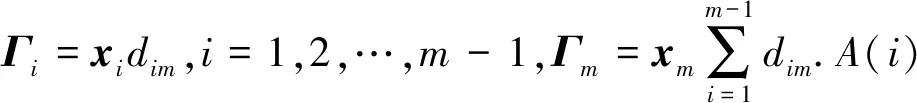
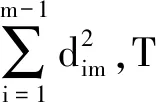
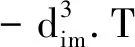
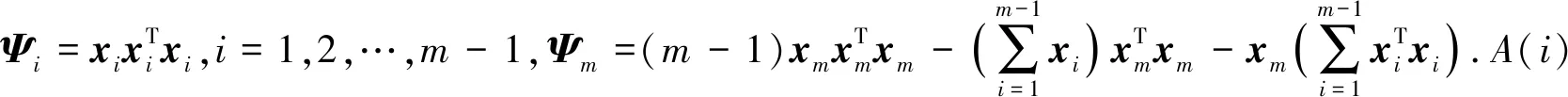
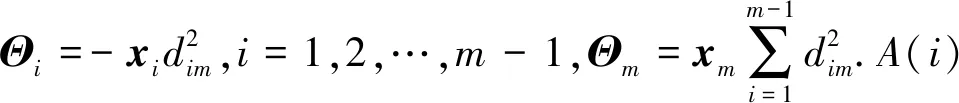
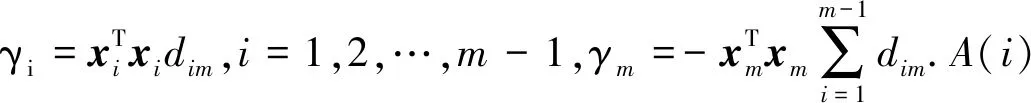

5.2 AMT场景的隐私保护协议分析
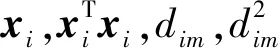

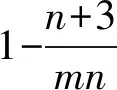
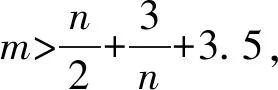


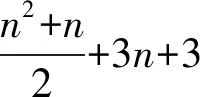
5.3 TMT场景的隐私保护协议分析
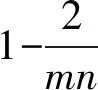


5.4 通信复杂性对比
11m2-22m-10km+15k+10,
6 仿真及结果分析







7 结 论
